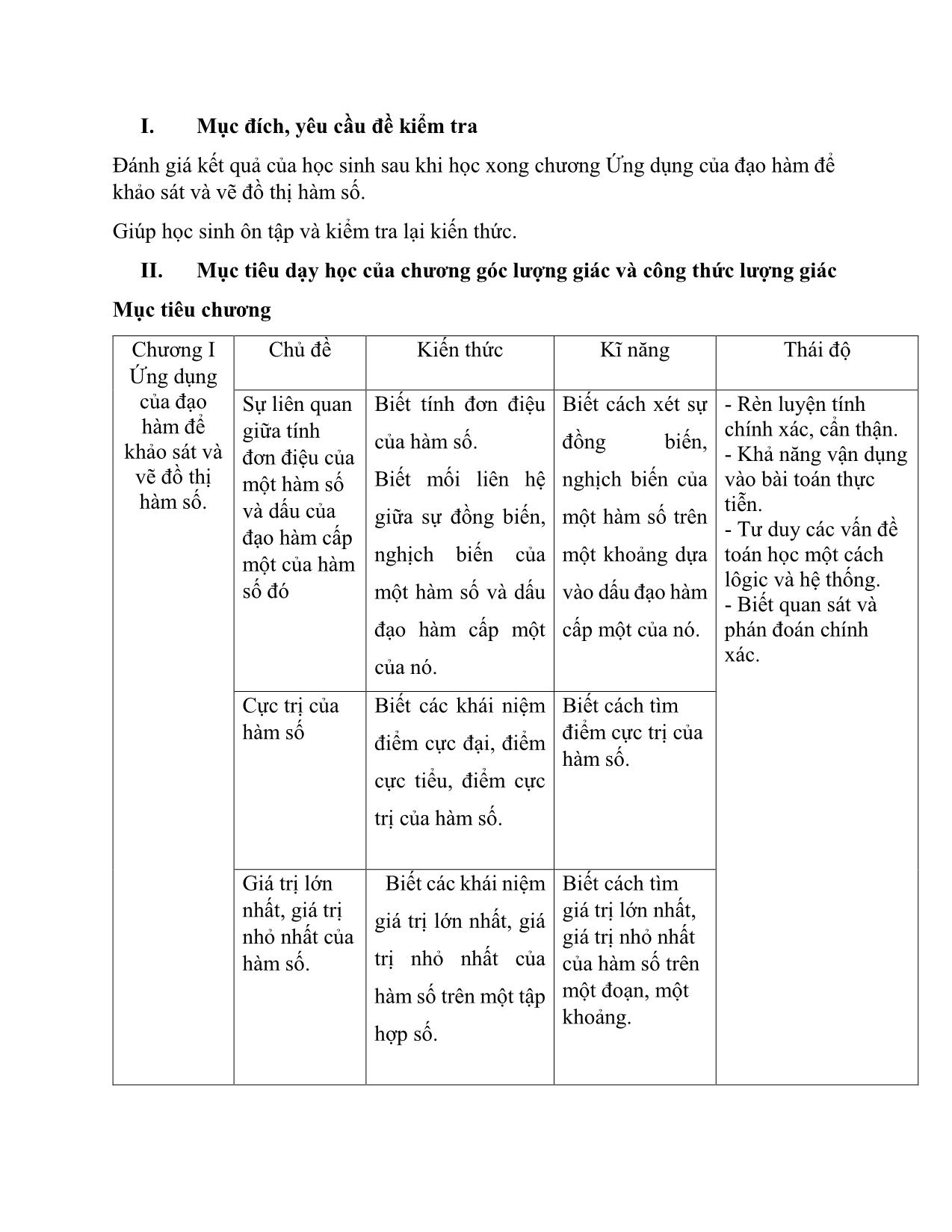
Đề tài Quá trình ra đề kiểm tra một tiết Giải tích 12, Chương I Ứng dụng đạo để khảo sát và vẽ đồ thị hàm số

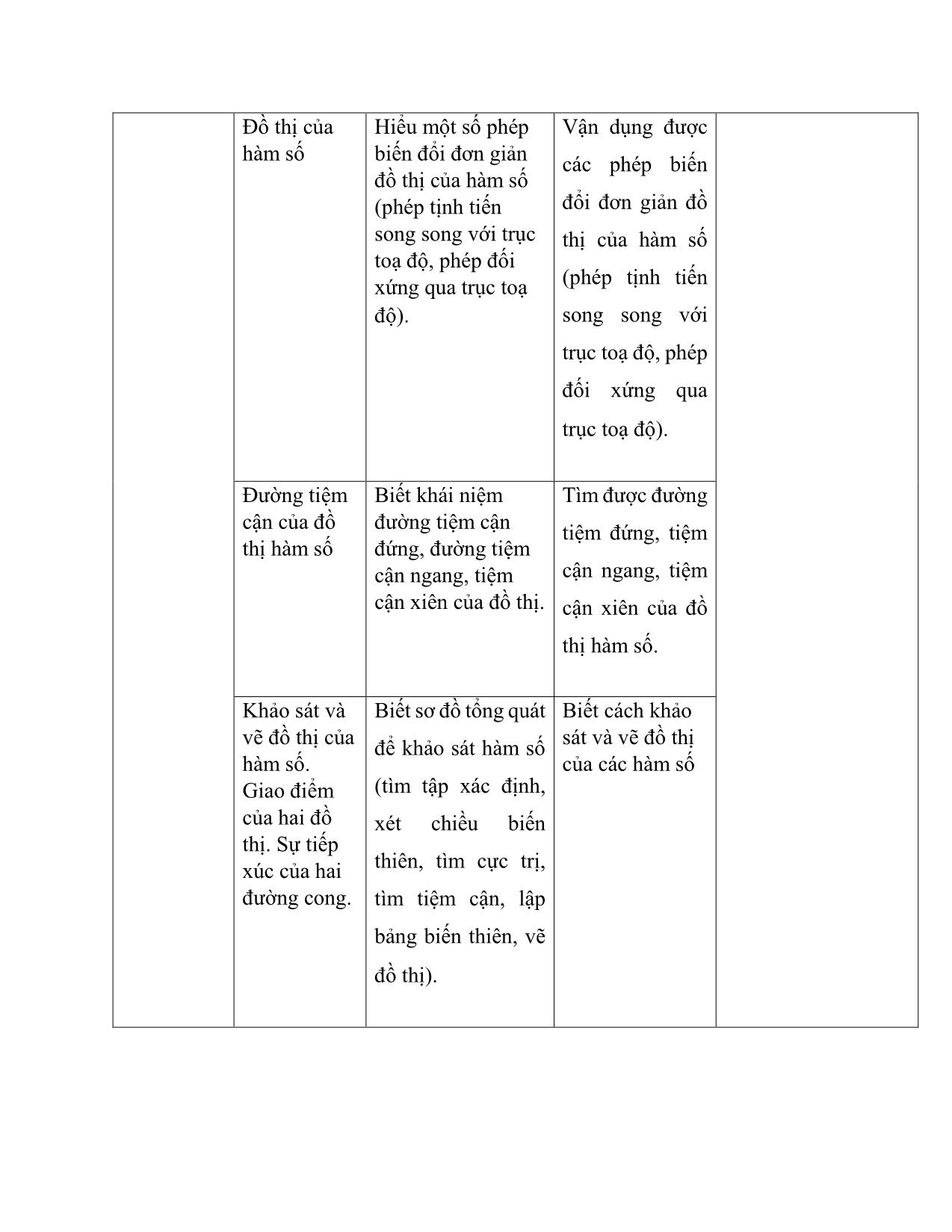
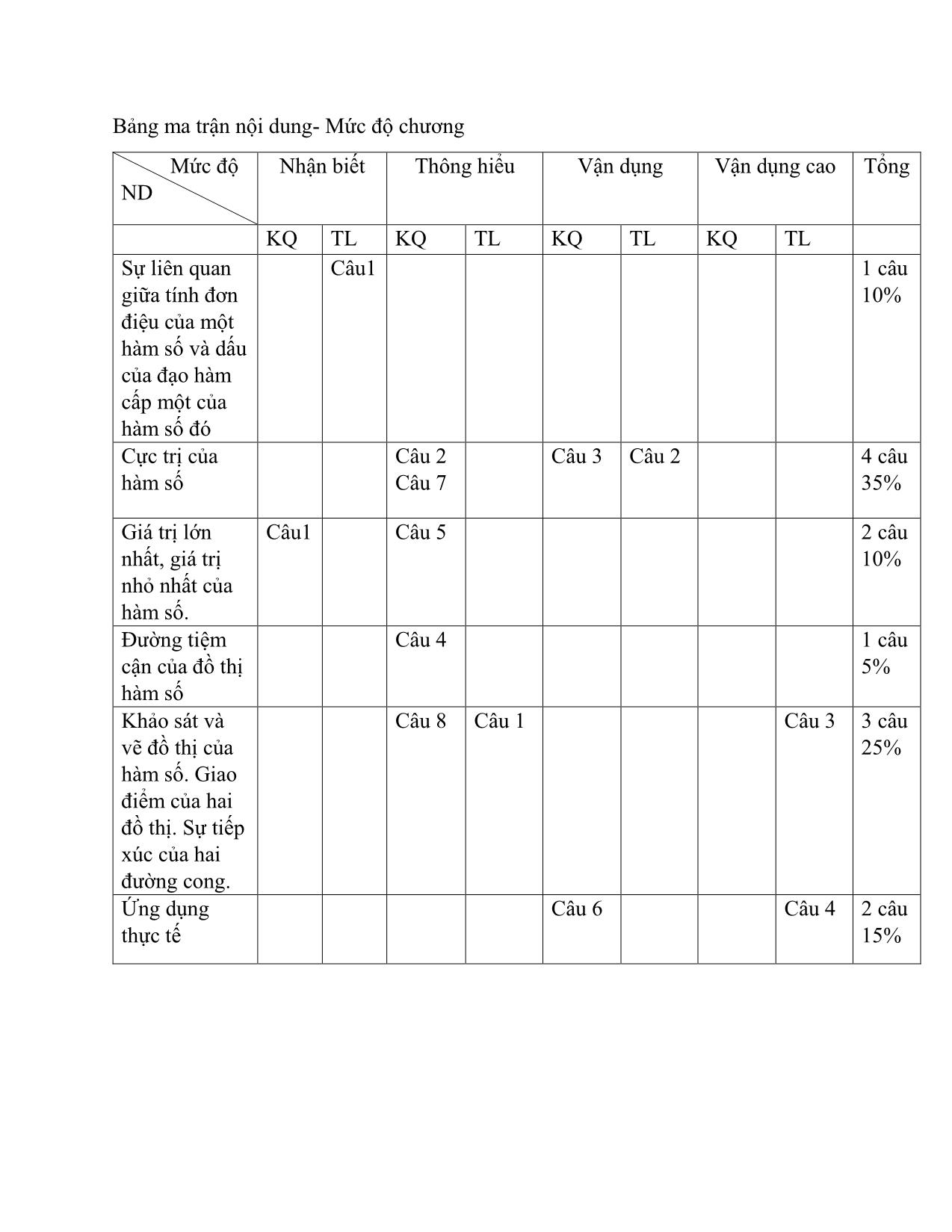
 TRƯỜNG ĐẠI HỌC SƯ PHẠM HUẾ 
 KHOA TOÁN HỌC 
 ĐỀ TÀI: Quá trình ra đề kiểm tra một tiết Giải tích 12, 
 chương I: Ứng dụng đạo để khảo sát và vẽ đồ thị hàm số. 
Học phần: Đánh giá kết quả giáo dục của học sinh. 
GVGD: TS. Nguyễn Đăng Minh Phúc 
Sinh viên: Phan Bá Thiên 
Lớp: Toán 3T 
Mã số SV: 16S1011076 
 Huế,12/2018 
 Mục lục 
Lời mở đầu ................................................................................................................. 3 
 I. Mục đích, yêu cầu đề kiểm tra.......................................................................... 4 
 II. Mục tiêu dạy học của chương góc lượng giác và công thức lượng giác .......... 4 
 III. Đề kiểm tra .................................................................................................... 7 
 IV. Mô tả đề kiểm tra .........................................................................................12 
Tài liệu tham khảo ....................................................................................................13 
 Lời mở đầu 
Kiểm tra, đánh giá là hoạt động không thể thiếu nhằm xác định hiệu quả của việc 
thực hiện mục tiêu dạy học, từ đó định hướng và thúc đẩy giáo viên đổi 
mới phương pháp dạy học, thúc đẩy học sinh đổi mới phương pháp học tập nhằm 
nâng cao chất lượng thực hiện mục tiêu giáo dục. Hoạt động đánh giá còn là để 
phát hiện những mặt tốt, mặt chưa tốt, khó khăn, vướng mắc và xác định nguyên 
nhân để đề ra các giải pháp nâng cao chất lượng dạy và học, hiệu quả giáo dục. 
Việc đánh giá trong giáo dục nói chung và giáo dục toán nói riêng cần phải thực 
hiện thường xuyên và liên tục. Trong giáo dục toán, kiểm tra 45 phút vào mỗi cuối 
chương học giúp giáo viên kiểm tra được kiến thức toán học thuộc vào chương đó 
mà học sinh thu nhận được, vừa gúp học sinh tổng kết được những kiến thức mình 
đã được trong chương vừa học. 
Trong chủ đề này, chúng ta sẽ tìm hiểu cách ra đề kiểm tra 45 phút cho học sinh 
lớp 12 chương Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số dưới hình thức 
trắc nghiệm kết hợp tự luận, từ đó thấy được quy trình ra đề để kiểm tra 45 phút là 
như thế nào để phù hợp với học sinh và mục tiêu dạy học. 
Lần đầu tiên làm đề kiểm tra, chắc chắn không tránh khỏi những sai sót, em rất 
mong nhận được những ý kiến đóng góp chân thành từ thầy và các bạn. 
 I. Mục đích, yêu cầu đề kiểm tra 
Đánh giá kết quả của học sinh sau khi học xong chương Ứng dụng của đạo hàm để 
khảo sát và vẽ đồ thị hàm số. 
Giúp học sinh ôn tập và kiểm tra lại kiến thức. 
 II. Mục tiêu dạy học của chương góc lượng giác và công thức lượng giác 
Mục tiêu chương 
 Chương I Chủ đề Kiến thức Kĩ năng Thái độ 
 Ứng dụng 
 của đạo Sự liên quan Biết tính đơn điệu Biết cách xét sự - Rèn luyện tính 
 hàm để chính xác, cẩn thận. 
 giữa tính của hàm số. đồng biến, 
 khảo sát và đơn điệu của - Khả năng vận dụng 
 vẽ đồ thị một hàm số Biết mối liên hệ nghịch biến của vào bài toán thực 
 hàm số. tiễn. 
 và dấu của giữa sự đồng biến, một hàm số trên 
 đạo hàm cấp - Tư duy các vấn đề 
 một của hàm nghịch biến của một khoảng dựa toán học một cách 
 lôgic và hệ thống. 
 số đó một hàm số và dấu vào dấu đạo hàm 
 - Biết quan sát và 
 đạo hàm cấp một cấp một của nó. phán đoán chính 
 xác. 
 của nó. 
 Cực trị của Biết các khái niệm Biết cách tìm 
 hàm số điểm cực đại, điểm điểm cực trị của 
 hàm số. 
 cực tiểu, điểm cực 
 trị của hàm số. 
 Giá trị lớn Biết các khái niệm Biết cách tìm 
 nhất, giá trị giá trị lớn nhất, giá giá trị lớn nhất, 
 nhỏ nhất của giá trị nhỏ nhất 
 hàm số. trị nhỏ nhất của của hàm số trên 
 hàm số trên một tập một đoạn, một 
 khoảng. 
 hợp số. 
Đồ thị của Hiểu một số phép Vận dụng được 
hàm số biến đổi đơn giản các phép biến 
 đồ thị của hàm số 
 (phép tịnh tiến đổi đơn giản đồ 
 song song với trục thị của hàm số 
 toạ độ, phép đối 
 xứng qua trục toạ (phép tịnh tiến 
 độ). song song với 
 trục toạ độ, phép 
 đối xứng qua 
 trục toạ độ). 
Đường tiệm Biết khái niệm Tìm được đường 
cận của đồ đường tiệm cận tiệm đứng, tiệm 
thị hàm số đứng, đường tiệm 
 cận ngang, tiệm cận ngang, tiệm 
 cận xiên của đồ thị. cận xiên của đồ 
 thị hàm số. 
Khảo sát và Biết sơ đồ tổng quát Biết cách khảo 
vẽ đồ thị của để khảo sát hàm số sát và vẽ đồ thị 
hàm số. của các hàm số 
Giao điểm (tìm tập xác định, 
của hai đồ xét chiều biến 
thị. Sự tiếp 
xúc của hai thiên, tìm cực trị, 
đường cong. tìm tiệm cận, lập 
 bảng biến thiên, vẽ 
 đồ thị). 
Bảng ma trận nội dung- Mức độ chương 
 Mức độ Nhận biết Thông hiểu Vận dụng Vận dụng cao Tổng 
ND 
 KQ TL KQ TL KQ TL KQ TL 
Sự liên quan Câu1 1 câu 
giữa tính đơn 10% 
điệu của một 
hàm số và dấu 
của đạo hàm 
cấp một của 
hàm số đó 
Cực trị của Câu 2 Câu 3 Câu 2 4 câu 
hàm số Câu 7 35% 
Giá trị lớn Câu1 Câu 5 2 câu 
nhất, giá trị 10% 
nhỏ nhất của 
hàm số. 
Đường tiệm Câu 4 1 câu 
cận của đồ thị 5% 
hàm số 
Khảo sát và Câu 8 Câu 1 Câu 3 3 câu 
vẽ đồ thị của 25% 
hàm số. Giao 
điểm của hai 
đồ thị. Sự tiếp 
xúc của hai 
đường cong. 
Ứng dụng Câu 6 Câu 4 2 câu 
thực tế 15% 
 III. Đề kiểm tra 
 A. Trắc nghiệm (4 điểm) 
Câu 1. Cho hàm số y = f(x) xác định trên tập D. Số M được gọi là giá trị lớn nhất 
của hàm số y= f() x trên tập D nếu 
 x D,() f x M
 A. x D,() f x M B. 
 x00 D,() f x = M
 x D,() f x M
 C. x D,() f x M D. 
 x00 D,() f x = M
Câu 2. Cho hàm số y = f(x) xác định, liên tục trên đoạn − 2;2 và có đồ thị là 
đường cong như hình vẽ. Hàm số f(x) đạt cực đại tại điểm nào dưới đây? 
 A. x = 2 B. x = -1 C. x = 1 D. x = - 2 
Câu 3. Hàm số y= x32 −6 x + 9 x + 5 , có giá trị cực đại bằng M; có giá trị cực tiểu bằng 
m. Khi đó Mm−=? 
 A. -4 B. 4 C. 2 D. -2 
 7
Câu 4. Tiệm cận ngang của đồ thị hàm số y = là : 
 x − 2
 A. y = 0 B. x = 2 C. x= 7 D. x = 0 
 x3
Câu 5. Giá trị nhỏ nhất của hàm số y= −3 x2 + 5 x − 1 trên đoạn [0;2] là: 
 3
 4 −1 −28
 A. B. −1 C. D. 
 3 3 3
Câu 6. Trong tất cả các khu vườn hình chữ nhật có cùng diện tích bằng 90m2 , khu 
vườn có chu vi nhỏ nhất bằng: 
 A. 16 10 m B. 10 10 m C. 9 10 m D. 12 10 m 
Câu 7. Số điểm cực trị của hàm số y= − x42 −23 x − là: 
 A. 0 B. 1 C. 2 D. 3 
Câu 8. Đồ thị sau là đồ thị của hàm số nào trong bốn hàm số dưới 
đây 
 -1 0 1
 A. y= x42 +21 x − B. y= − x42 + 2 x 
 42 42
 C. y= x −21 x − D. y=− x2 x -1 
 B. Tự luận 
Câu 1: Cho hàm số y= x32 + 3x − mx − 4 
1.Khảo sát và vẽ đồ thị khi m = 0 
2.Tìm m để hàm số đồng biến trên khoảng (− ;0) . 
Câu 2: Tìm m để hàm số y= − x3 +( m +3) x 2 −( m 2 + 2 m) x − 2 đạt cực đại tại x=2 
 mx+ 2
Câu 3: Cho hàm số y = có đồ thị là (C ) . Tìm m để trên đồ thị (C ) có 2 
 x1− m m
điểm P, Q cách đều 2 điểm A(− 3;4) , B( 3;− 2) và diện tích tứ giác APBQ bằng 24. 
Câu 4. Một đường dây điện được nối từ một nhà máy điện ở A đến một hòn đảo ở 
C như hình vẽ. Khoảng cách từ C đến B là 1 km. Bờ biển chạy thẳng từ A đến B 
với khoảng cách là 4 km. Tổng chi phí lắp đặt cho 1 km dây điện trên biển là 40 
triệu đồng, còn trên đất liền là 20 triệu đồng. Tính tổng chi phí nhỏ nhất để hoàn 
thành công việc trên(làm tròn đến hai chữ số sau dấu phẩy). 
Đáp án 
Phần trắc nghiệm: Mỗi câu 0.5 điểm. 
Câu 1 Câu 2 Câu 3 Câu 4 Câu 5 Câu 6 Câu 7 Câu 8 
B A B A B D B D 
Phần tự luận: 
 Câu Đáp án Điểm 
 1 Chiều biến thiên: 0.5 2 
 Giới hạn của hàm số tại vô cực: 
 lim y= − ; lim y = + 
 xx→− →+ 
 Bảng biến thiên: 
 Ta có: y = 3x2 + 6x = 3x( x + 2) 
 y = 0 3x( x + 2) = 0 x = 0 hoặc x2=− 
 Hàm số đồng biến trên các khoảng (− ;2 − ) và (0;+ ) , 
 nghịch biến trên khoảng (−2 ; 0) . 
 Hàm số đạt cực đại tại điểm x2=− ; giá trị cực đại của hàm 
 số là y(−= 2) 0 
 Hàm số đạt cực tiểu tại điểm x0= ; giá trị cực tiểu của hàm 
 số 
 là y( 0) =− 4 
 Giới hạn của hàm số tại vô cực : 
 lim y= + ; lim y = − . 
 xx→− →+ 
 Bảng biến thiên: 0.5 
 x − −2 0 
 + 
 y' + 0 − 0 − 
 y 0 
 + 
 − −4 
 Đồ thị : 
 Cho x= − 3 y = − 4 ; x = 1 y = 0 
 Hàm số y= x32 + 3x − mx − 4 đồng biến trên khoảng (− ;0) 
 y = 3x2 + 6xm0,x −  ( − ;0) . 
 Xét: gx( ) = 3x2 + 6xm,x − ( − ;0) 
 g ( x) = 6x + 6 g( x) = 0 x = − 1 
 Bảng biến thiên : 
 x − −1 
 0 
 g'(x) − 0 
 + 
 g(x) + 
 −m 
 −3 – m 
 Nhìn vào bảng biến thiên ta thấy: 
 y'gx=( ) = 3x2 + 6xm0,x −  − ( ;0) −− − 3m0 m 3 
 Vậy khi m3 − thì yêu cầu của bài toán được thỏa mãn . 
2 Để hàm số y= − x3 +( m + 3) x 2 − ( m 2 + 2 m ) x − 2 đạt cực đại tại x = 2 2 
 2 thì 
 mmy=0, = 2, ' =−++−+ 3 xmxmmy22 2( 3) ( 2 ); '' =−++ 6 xm 2( 3) 
 y'(2)= 0
 Hàm số đã cho đạt cực đại tại x = 2 
 y''(2) 0
 −12 + 4(m + 3) − m22 − 2 m = 0 m − 2 m = 0
 −12 + 2mm + 6 0 0
 m = 0
 m = 2
 Kết luận: Giá trị m cần tìm là m=0, m=2 
3 Phương trình hoành độ giao điểm của (Cm ) và PQ: 1 1 
 mx+ 2
 =+x1 x2 − mx − 3 = 0, x1 (1) 
 x1−
 PQ cắt (Cm ) tại 2 điểm phân biệt P, Q khi và chỉ khi phương 
 trình (1) có 2 nghiệm phân biệt khác 1 , tức là 
 0
 m2 − 
 m+ 2 0
 Với m2 − , phương trình (1) có 2 nghiệm x,1 x2 . 
 2
 Gọi tọa độ P( x11 ;x+ 1) , Q( x22 ;x+ 1) PQ = 2( x21 − x ) 
 Diện tích tứ giác APBQ bằng 24 =d( A;PQ) .PQ 24 
 2 2
 3 2 2( x21 − x) = 24 (x1 + x 2) − 4x 1 x 2 = 16 (2) 
 Theo định lý Vi – et , ta có: x12+= x m, x12 .x=− 3 
 Thay vào (2) ta được m2 + 12 − 16 = 0 m = − 2 hoặc m2= 
 Đối chiếu điều kiện, ta thấy m2= thỏa mãn bài toán. 
4 0.25 
 Gọi M là điểm trên đoạn AB để lắp đặt đường dây điện ra 0.25 
 biển nối với điểm C . 
 Đặt 
 BMxAM= =− 4 xCM =+−= 1( 4 x)2 17 −+ 8 xxx2 ,  0;4 
 Khi đó tổng chi phí lắp đặt là : y= x.20 + 40 x2 − 8 x + 17 đơn vị 
 là triệu đồng. 
 x − 4 x2 −8 x + 17 + 2( x − 4) 0.5 
 y =20 + 40. = 20. . 
 x22−8 x + 17 x − 8 x + 17
 12− 3
 y =0 x2 − 8 x + 17 = 2( 4 − x) x = 
 2
 Ta có 
 12− 3
 y =80 + 20 3 114,64; y( 0) = 40 17 164,92; y( 4) = 120 
 3
 Tính tổng chi phí nhỏ nhất để hoàn thành công việc trên là 
 114,64. 
 IV. Mô tả đề kiểm tra 
Đề kiểm tra gồm hai phần trắc nghiệm 40% và tự luận 60% các câu hỏi được xếp 
theo 4 mức độ ở bảng mô tả phần trắc nghiệm. Đề kiểm tra giúp học sinh củng cố 
kiến thức và giáo viên dựa vào đó để đánh giá quá trình học tập của học sinh. Do 
yêu cầu của chương nên phần vẽ đồ thị hàm số được vào phần tự luận, nội dung đề 
có 2 câu hỏi thực tế nhằm kiểm tra mức độ vận dụng kiến thức của chương trong 
đời sống. Có 2 câu hỏi vận dụng cao điểm 9,10 các câu còn lại học sinh nắm vững 
kiến thức và có ý thức rèn luyện giải các bài tập trong chương đều có thể làm được. 
Đề ra hi vọng phân loại được học sinh nhằm định hướng và chuẩn bị cho kì thi học 
kì I và thi THPT Quốc gia. 
 Tài liệu tham khảo 
[1] Sách giáo khoa giải tích (Cơ bản), NXB Giáo dục Việt Nam, 2016. 
[2] Sách bài tập giải tich (Cơ bản), NXB Giáo dục Việt Nam, 2016. 
[3] Đánh giá trong giáo dục toán, Trần Vui – Nguyễn Đăng Minh Phúc, 2012. 
[4] Chuẩn kiến thức, kĩ năng Toán lớp 12 (cơ bản)