Bài tập Cấu trúc dữ liệu và giải thuật

n chữ số.
Số nguyên lớn ở đây là số có thể có đến vài trăm chữ số. Để lưu trữ các số nguyên lớn này ta có thể dùng chuỗi (mỗi ký tự của chuỗi là một chữ số) hoặc dùng mảng một chiều (mỗi phần tử của mảng một chiều là một chữ số). Tuy nhiên trong hai phương án này thì phương án dùng mảng một chiều để lưu trữ sẽ có thuật toán tốt hơn.
b.Thực hiện phép trừ hai số nguyên lớn.
c.Thực hiện phép nhân hai số nguyên lớn.
d.Thực hiện phép chia hai số nguyên lớn.
BT1-12.Cho dãy n số nguyên {ai, ở đây giả sử i=1..n} Dãy con liên tiếp là dãy mà thành phần của nó là các thành phần liên tiếp nhau trong {a}, ta gọi tổng của dãy con là tổng tất cả các thành phần của nó. Tìm tổng lớn nhất trong tất cả các tổng của các dãy con của {a}.
Ví dụ nếu n = 7;
4 	–5 	6 	–4 	2 	3 	-7
Thì kết quả tổng là 7.
Phần gợi ý:
BT1.9.
Algorithms1: O(N2)
	float s=1;
for (int i=1;i<=n;i++)
s=s+pow(x,i)/giaithua(i);// giaithua(i) = i!=1.2.3.i 
	Độ phức tạp theo cách này là O(N2), tuy nhiên chương trình không thể thực hiện được khi n lớn; chẳng hạn n =100 - do phép tính giai thừa của n không thể thực hiện..
Algorithms2: O(N2)
float s=1,p;
for (int i=1; i<=n;i++)
{
p=1;
for (int j=1; j<=i;j++)
p=p*x/j;
s=s+p;
}
	Độ phức tạp theo cách này vẫn là là O(N2), tuy nhiên chương trình đã không cần tính giai thừa của n.
Algorithms3: O(N) – độ phức tạp tuyến tính
float s=1,p=1;
for (int i=1;i<=n;i++)
{
	p=p*x/i;
	s=s+p;
}
BT1-11.a.
Nhập m chữ số của số a, lưu vào mảng một chiều a.
Nhập n chữ số của số b, lưu vào mảng một chiều b. 
Giả sử ta có hai số a=97895 và b = 6478
i
0
1
2
3
4
a[i]
9
7
8
9
5
B[i]
6
4
7
8
Lưu ý nếu khi nhập mà không giống hàng bên phải thì kết quả sẽ sai, ta có thể tiến hành nhập hai số a,b theo cách sau để khắc phục tình trạng này:
	Đặt max là số lớn nhất trong hai giá trị m và n.
	Việc nhập hai số a ,b được tiến hành như sau:
	for i=max-m+1;i<=max;i++
	cin>>a[i];
	for i=max-n+1;i<=max;i++
	cin>>b[i];
	Sau đó thực hiện phép cộng như cách thông thường:
	remember=0;
	for (i=max; i >=1;i--)
	{
c[i]=(a[i]+b[i]+remember)%10;
	remember=(a[i]+b[i]+remember)/10;
	}
	c[0]=remember; 
mảng c[i] chính là tổng của hai số a và b.
Lưu ý là giá trị c[0] này chỉ xuất ra khi nó khác 0.
Đoạn chương trình xuất kết quả như sau:
	if (c[0]!=0) cout<<c[0];
for (i=1;i<=max;i++) 
cout<<c[i];
Dữ liệu thử:
m =5; n = 4;
a = 97895, b = 6478
Giá trị của các phần tử của hai mảng a và b là:
a[1] = 9, 	a[2]=7;	a[3]=8;	a[4]=9.	a[5]=5.
b[2] = 6, 	b[3]=4;	b[4]=7;	b[5]=8
BT1-12
Algorithms1: O(N3)
Thuật toán đơn giản nhất có thể viết ngay là: Xét tất cả các cặp số nguyên L và U thỏa mãn 1 £ L £ U £ n; đối với mỗi cặp như vậy ta tính tổng của dãy con a[L..U] và so sánh tổng này với giá trị lớn nhất hiện có:
for (L=1;L<=n;L++)
 for (U=L;U<=n;U++)
 {
sum=0;
 for (int I=L;I<=U;I++)
	sum=sum+a[I];
 maxsofar=max(maxsofar,sum);
 }
Chương trình này tuy dễ hiểu, nhưng nó chạy rất chậm. Thuật toán này có độ phức tạp là O(n3). Các bạn xem nếu n=10000 thì thời gian dành cho thuật toán này là quá lớn.
Algorithms2:O(N2)
Ta có thể cải tiến thuật toán trên để có thuật toán với độ phức tạp là O(n2) bằng cách sử dụng hệ thức :
Tổng a[L..U]= Tổng a[L..U-1]+a[U]
 maxsofar=0;
 for (L=1;L<=n;L++)
 {
sum=0;
 for (U=L;U<=n;U++)
	{
	sum=sum+a[U];
	maxsofar=max(maxsofar,sum);
	}
}
Algorithms3:O(N)
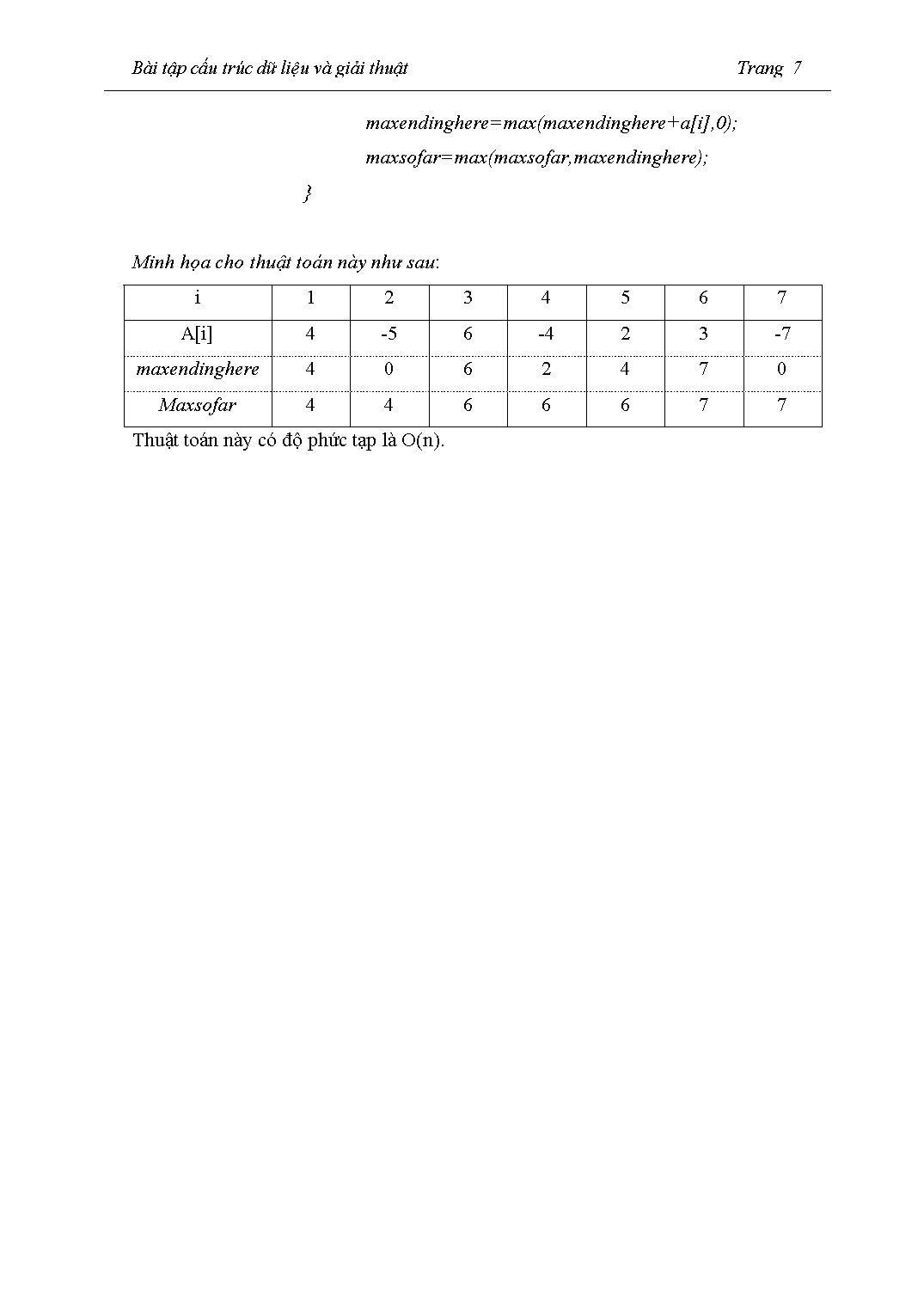
	Tổng lớn nhất trong dãy con a[1..i] là tổng lớn nhất trong dãy con a[1..i-1] - gọi là maxsofar hoặc tổng lớn nhất trong tất cả các tổng của các dãy con kết thúc tại i - gọi là maxendinghere. Chúng ta có nhận xét rằng: Dãy con lớn nhất kết thúc tại i là dãy con lớn nhất kết thúc tại vị trí i-1 được bổ sung thêm phần tử a[i] ở cuối hoặc là dãy con rỗng trong trường hợp tổng của dãy con nhận được là số âm. Ta có thuật toán như sau:
maxsofar=0;
	maxendinghere=0;
	 for (i=1; i<=n;i++)
	 {
	 maxendinghere=max(maxendinghere+a[i],0);
	 maxsofar=max(maxsofar,maxendinghere);
	 }
Minh họa cho thuật toán này như sau:
i
1
2
3
4
5
6
7
A[i]
4
-5
6
-4
2
3
-7
maxendinghere
4
0
6
2
4
7
0
Maxsofar
4
4
6
6
6
7
7
Thuật toán này có độ phức tạp là O(n).
Chương 2
Tìm kiếm & sắp xếp
Viết chương trình hoàn chỉnh cho các bài toán sau đây
BT2-1.Cho dãy số.
84	32	13	64	1	55	48
Hãy mô phỏng sắp xếp tăng dần dãy số trên bằng các thuật toán toán chọn trực tiếp, đổi chỗ trực tiếp, nổi bọt, chèn trực tiếp.
BT2-2.Cho dãy n số nguyên a[0],a[1],,a[n-1] đã được sắp xếp tăng dần và một số nguyên x. 
a.Hãy viết hàm tìm kiếm nhị phân kiểm tra xem x có thuộc dãy số trên hay không ? Nếu tìm thấy trả về giá trị i nhỏ nhất mà a[i] = x, nếu không trả về giá trị -1.
b.Cho biết k số phần tử lớn nhất của dãy.
	Ví dụ với n=12
	9	6	2	7	9	9	6	5	7	9	6	7
	Nếu k=5 thì kết quả là 9, 9, 9, 9, 7
BT2-3.Cho mảng một chiều n phần tử. Sắp xếp các số nguyên tố tăng dần, các số khác giữ nguyên giá trị và vị trí.
BT2-4.Cho ma trận hai chiều m dòng, n cột. Hãy sắp tăng dần các phần tử theo chiều từ trái qua phải và từ trên xuống dưới.
BT2-5.Viết chương trình cho các phương pháp sắp xếp sau:
a.Đổi chỗ trực tiếp
b.Chọn trực tiếp
c.Chèn trực tiếp
d.Nổi bọt.
BT2-6.Cho dãy số.
84	32	13	64	1	55	48
Hãy mô phỏng sắp xếp tăng dần bằng các thuật toán toán Quick Sort, Merge Sort, Heap Sort, Shell Sort qua dãy số trên.
BT2-7.Cho mảng một chiều gồm n phần tử là các số nguyên. Hãy sắp xếp các số chẵn trong mảng theo thứ tự tăng, sắp xếp các số lẻ theo thứ tự giảm dần, các số 0 giữ nguyên vị trí.
BT2-8.Cho hai tập tin văn bản chứa các số nguyên đã được sắp tăng dần. Hãy trộn hai tập tin này để được một tập tin cũng được sắp tăng dần (không dùng mảng).
BT2-9.Cho một tập tin văn bản. Hãy cho biết số lượng của các số nguyên tố, chính phương, hoàn hảo, số Amstrong trong tập tin này.
BT2-10.Hãy vẽ cây phân hoạch đệ qui của thuật toán Quick-Sort trong trường hợp xấu nhất. Từ đó, chứng tỏ rằng chi phí thuật toán Quick-sort trong trường hợp này là O(n2).
BT2-11.Hãy cho biết số phần tử tối thiểu và tối đa trong một heap có chiều cao h ?
BT2-12.a.Viết chương trình cho phương pháp sắp xếp Quick sort.
b.Viết chương trình cho phương pháp sắp xếp cây (heap sort).
c.Viết chương trình cho phương pháp sắp xếp trộn trực tiếp (merge sort).
d.Viết chương trình cho phương pháp sắp xếp với độ dài bước giảm dần (shell sort). 
Chương 3
Cấu trúc danh sách liên kết
Viết chương trình hoàn chỉnh cho các bài toán sau đây
BT3-1.Cho một danh sách liên kết đơn l, mỗi nút là một số nguyên dương.
a.Tìm phần tử lớn nhất danh sách l.
b.Tìm tổng các phần tử của danh sách l.
c.Đếm xem trong danh sách l có bao nhiêu số nguyên tố ? 
d.Đếm xem trong danh sách có bao nhiêu số âm ? bao nhiêu số bằng 0 ? bao nhiêu số dương ?
e.Đếm xem trong danh sách có bao nhiêu số bằng x ?
f.Tìm phần tử dương nhỏ nhất trong danh sách.
BT3-2. Cho một danh sách liên kết đơn l, mỗi nút là một số nguyên dương.
a.Xóa phần tử đầu tiên trong danh sách.
b.Xóa phần tử cuối cùng trong danh sách.
c.Xóa một phần tử được trỏ bởi con trỏ q.
d.Xóa một phần tử ngay trước phần tử được trỏ bởi con trỏ q.
e.Xóa một nút có giá trị k.
f.Xóa tất cả các số có giá trị nguyên tố.
BT3-3. Cho một danh sách liên kết đơn l, mỗi nút là một số nguyên dương.
a.Hãy tạo danh sách l1 chỉ chứa các số nguyên tố từ danh sách l.
b.Tách danh sách l thành 2 danh sách: một danh sách chứa toàn số chẵn, một danh sách chứa toàn số lẻ.
c.Sắp xếp các phần tử của l giảm dần theo phương pháp chọn trực tiếp.
BT3-4.Viết chương trình thực hiện các yêu cầu sau:
a.Khai báo cấu trúc dữ liệu của một danh sách liên kết đơn các tỉnh. Biết rằng thông tin của mỗi tỉnh bao gồm: tên tỉnh, diện tích, dân số
b.Cài đặt các thao tác cơ bản cho danh sách liên kết đơn các tỉnh (thêm, sửa , xóa, duyệt).
c.Tính tổng diện tích của tất cả các tỉnh trong danh sách liên kết
d.Tìm địa chỉ của node chứa tính có diện tích lớn nhất trong danh sách liên kết.
e.Tìm một tỉnh có dân số lớn nhất.
f.Sắp xếp danh sách tăng dần theo diện tích.
BT3-5.Viết chương trình thực hiện các yêu cầu sau:
a.Khai báo cấu trúc dữ liệu của một danh sách liên kết đơn để lưu tọa độ các đỉnh của một đa giác lồi trong mặt phẳng OXY.
b.Tính chu vi của đa giác.
c.Tính diện tích của đa giác.
BT3-6.Cho một danh sách liên kết, mỗi nút chứa một số nguyên.
a.Thêm một phần tử có giá trị x vào đầu danh sách
b.Chỉ giữ lại một giá trị trong số các giá trị giống nhau.
c.Kiểm tra xem danh sách có được sắp xếp tăng dần hay không?
d.Đảo ngược danh sách.
e.Sắp xếp các số chẵn trong danh sách theo thứ tự tăng, sắp xếp các số lẻ theo thứ tự giảm dần, các số 0 giữ nguyên vị trí..
BT3-7.Cộng hai đa thức (mỗi node có 3 thành phần: hệ số khác 0 của một số hạng, số mũ tương ứng và mốc nối tới node tiếp theo).
BT3-8.Ta có 4 lựa chọn: 1. Stack; 2. Queue; 3. List; 4. Cả 3 CTDL này đều không thích hợp. Trong mỗi tình huống sau, hãy cho biết áp dụng lựa chọn nào là thích hợp nhất:
a.Các khách hàng tại quầy bán vé xe lửa lấy số thứ tự để mua vé
b.Một danh sách tên theo thứ tự ABC
c.Các số nguyên cần phải sắp thứ tự
d.Danh sách các món hàng đã bán trong ngày tại quầy thâu ngân trong siêu thị
e.Chương trình có sử dụng kỹ thuật Back-tracking
f.Các máy bay đang chờ đáp xuống phi trường
BT3-9.Tính giá trị của đa thức P(x) với x và các hệ số cho biết trước được tổ chức dưới dạng một danh sách liên kết (mỗi node có 3 thành phần: hệ số khác 0 của một số hạng, số mũ tương ứng và mốc nối tới node tiếp theo).
BT3-10.Hoàn chỉnh các thao tác trên Stack và Queue.
BT3-11.a.Cài đặt thuật toán sắp xếp chèn trực tiếp trên xâu kép
b.Sắp xếp danh sách tăng dần thuật toán Quick sort.
c.Cài đặt thuật toán Mergesort trên xâu kép.
d.Hãy thể hiện thuật toán sắp xếp nổi bọt trên danh sách liên kết kép.
BT3-12.Tính giá trị của một biểu thức dạng chuỗi ký tự bao gồm các chữ số và các phép toán +,-,*,/ , % và dấu đóng mở ngoặc đơn.
Ví dụ: (( 2 + 3 )*2) – 4/2 = 12
Chương 4
Cấu trúc cây
Viết chương trình hoàn chỉnh cho các bài toán sau đây
BT4-1.Cho cây như hình sau. Hãy trả lời các câu hỏi sau:
A
G
C
J
E
F
B
H
I
D
M
N
O
K
L
a.Các nút nào là nút lá ?
b.Các nút nào là nút nhánh ?
c.Cha của nút G là nút nào ?
d.Con của nút C là các nút nào ?
e.Các nút nào là anh em của nút B ?
f.Mức của D, của L là bao nhiêu ?
g.Bậc của B, bậc của D là bao nhiêu ?
h.Bậc của cây này là bao nhiêu ?
i.Chiều cao của cây này là bao nhiêu ?
j.Độ dài từ A đến F, từ A dến G là bao nhiêu ?
k.Có bao nhiêu đường đi từ gốc A có độ dài 3 trên cây này ?
BT4-2.a.Hãy vẽ cây nhị phân tìm kiếm T biết rằng khi duyệt cây T theo thứ tự Node – Left - Right thì được dãy như sau: 9, 4, 1, 3, 8, 6, 5, 7, 10, 14, 12, 13, 16, 19.
-Hãy duyệt cây T trên theo thứ tự left – right – node, left -node-right.
-Liệt kê các nút lá của cây ? các nút nhánh của cây ?
-Hãy vẽ lại cây sau khi xoá nút 10 sao cho T vẫn là cây nhị phân tìm kiếm.
b.Cho cây nhị phân tìm kiếm T gồm 12 số nguyên với phép duyệt LRN cho kết quả như sau: 1,3,2,6,7,5,4,10,9,12,11,8
-Hãy vẽ cây nhị phân tìm kiếm T.
-Duyệt cây T theo thứ tự NLR
-Vẽ lại cây sau khi xoá nút 8.
c.Hãy cây nhị phân tìm kiếm T gồm 11 số nguyên, với thứ tự các nút được cho như sau: 14(gốc), 11, 9, 18, 16, 20, 30, 10, 17, 1, 15
Hãy duyệt cây trên theo các thứ tự node- left-right, left- node-right, left- right- node.
Hãy cho biết chiều cao của cây T.
4
7
2
9
5
1
33
6
BT4-3.Cho cây nhị phân T (nút gốc có giá trị là 4) như hình vẽ bên:
-Cây T có phải là cây nhị phân tìm kiếm không ?
-Hãy duyệt cây T theo các thứ tự node-left-right, left-node-right, left- right- node.
-Cây T có chiều cao bao nhiêu ? 
-Liệt kê các nút lá của cây T.
-Liệt kê các nút nhánh của cây T.
A
B
C
D
E
G
F
H
I
J
BT4-4.Cho cây nhị phân như hình vẽ sau. 
Hãy viết dày các nút được thăm khi 
duyệt cây này theo 
a.thứ tự trước
b.thứ tự giữa 
c.thứ tự sau.
BT4-5.Cho cây nhị phân tìm kiếm T, mỗi nút chứa một số nguyên. Hãy viết các hàm thực hiện các yêu cầu sau:
a.Số nút lá.
b.Số nút có đúng 1 cây con.
c.Viết hàm đếm số nút có bậc bằng 2 trong cây nhị phân (hãy kiểm nghiệm lại rằng số nút lá luôn bằng số nút bậc 2 cộng thêm 1)
d.Số nút có khoá nhỏ hơn x (giả sử T là cây nhị phân tìm kiếm).
e.Số nút có khoá nhỏ hơn x và lớn hơn y (giả sử T là cây nhị phân tìm kiếm)
f.Đếm xem trong cây T có bao nhiêu số chẵn, bao nhiêu số lẻ ?
g.Kiểm tra xem giá trị k có trong cây T không ?
h.Đếm xem trong cây có bao nhiêu nút có giá trị âm? bao nhiêu nút có giá trị dương?
i.Kiểm tra xem giá trị x có trong cây không ?
j.Tìm giá trị lớn nhất, giá trị nhỏ nhất của cây.
k.Tìm phần tử dương nhỏ nhất của cây.
BT4.6.Cho cây nhị phân tìm kiếm T, mỗi nút chứa một số nguyên. Hãy viết các hàm thực hiện các yêu cầu sau:
a.Chiều cao của cây.
b.Tìm độ lệch của cây.
c.Xóa phần tử có giá là x trong cây
d.Xóa các số nguyên tố ra khỏi cây
e.Thêm một phần tử có giá trị x vào trong cây để cây vẫn là cây nhị phân tìm kiếm.
BT4-7.Cho cây nhị phân tìm kiếm T, mỗi nút chứa một số nguyên. Hãy viết các hàm thực hiện các yêu cầu sau:
a.Đếm số lượng nút nằm ở mức thứ k.
b.In ra tất cả các nút ở mức thứ k của cây T
c.In ra tất cả các nút theo thứ tự tầng 0 đến tầng thứ h-1 của cây T( h là chiều cao của cây)
BT4-8.Cho một cây nhị phân biểu diễn 1 biểu thức toán học. Biết rằng gốc của cây là Proot, mỗi nút có thuộc tính key (kiểu chả) , chứa 1 phép tính(+,- , *,/) hay một giá trị nguyên (các nút lá). Hãy viết hàm tính giá trị biểu thức chứa trong cây
BT4-9.Hãy nêu định nghĩa của cấu trúc dữ liệu của cây nhị phân tìm kiếm(CNPTK). Khai báo kiểu CNPTK có tên là TREE mà mỗi phần tử chứa một số nguyên và thực hiện các công việc sau:
a.Xây dựng hàm tìm kiếm phần tử có khóa x trên CNPTK T(giá trị trả về của hàm là con trỏ trỏ đến phần tử tìm được) hoặc bảng NULL, nếu không tìm thấy.
b.Xây dựng hàm đếm số phần tử có khóa lớn hơn k trên CNPTK T.
BT4-10.Viết chương trình quản lý một danh bạ điện thoại đơn giản bao gồm các thông tin: số thuê bao, họ tên chủ thuê bao, địa chỉ. Chương trình cho phép cập nhật: thêm/xoá/ sửa và tìm kiếm thông tin về một số thuê bao nào đó.
BT4-11.Cho một cây nhị phân T, mỗi nút là một số nguyên. Hãy viết các hàm thực hiện các yêu cầu sau:
a.Hãy đếm số nút của cây.
b.Cho biết chiều cao của cây AVL
c.Kiểm tra xem T có phải là cây nhị phân tìm kiếm không ?
d.Kiểm tra xem T có phải là cây cân bằng hoàn toàn không ?
e.Kiểm tra xem T có phải là cây nhị phân cân bằng không ?
f.Thêm một phần tử vào cây AVL
g.Hủy một phần tử trên cây AVL.
BT4-12.Cho cây nhị phân T trong đó thông tin tại mỗi nút trong cây biểu diễn các thành phần thông tin của một độc giả. Biết rằng một độc giả gồm những thành phần: Mã độc giả, tên độc giả, ngày sinh, địa chỉ, ngày lập thẻ.
a.Tìm địa chỉ của độc giả lớn tuổi nhất trong cây.
b.Liệt kê các độc giả trong cây sinh sau năm 1975
c.Đếm số lượng node có đủ 2 cây con có ngày lập thẻ trong ngày 09/07/2009.
d.Tìm kiếm địa chỉ theo mã độc giả.
e.Liệt kê các độc giả trong cây.