Bài giảng Toán rời rạc - Chương: Tô màu đỉnh của đồ thị - Trần Vĩnh Đức

Tô màu đỉnh của đồ thị
 Trần Vĩnh Đức
 HUST
 Ngày 24 tháng 7 năm 2018
 1 / 44
Tài liệu tham khảo
 ▶ Norman L. Biggs, Discrete Mathematics, Oxford University
 Press, 2002.
 2 / 44
Nội dung
 Định nghĩa và ví dụ
 Thuật toán tham lam tô màu đỉnh
 Đồ thị hai phần
 Bài tập
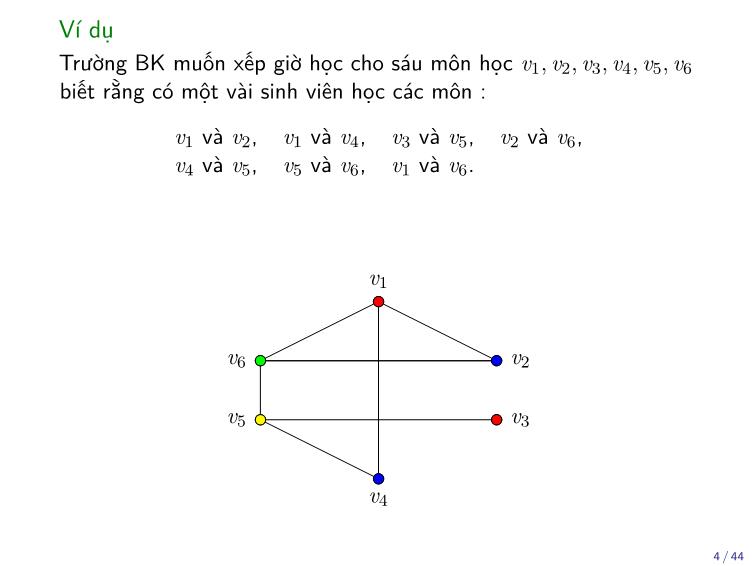
Ví dụ
Trường BK muốn xếp giờ học cho sáu môn học v1, v2, v3, v4, v5, v6
biết rằng có một vài sinh viên học các môn :
 v1 và v2, v1 và v4, v3 và v5, v2 và v6,
 v4 và v5, v5 và v6, v1 và v6.
 v1
 v6 v2
 v5 v3
 v4
 4 / 44
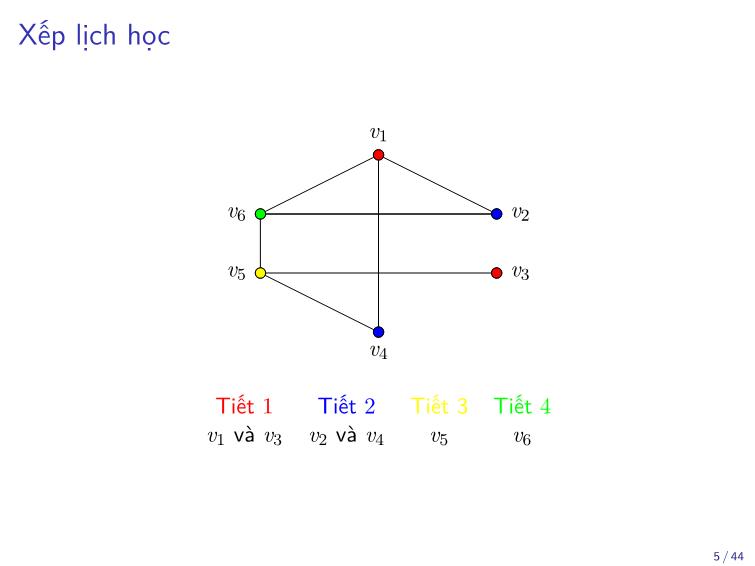
Xếp lịch học
 v1
 v6 v2
 v5 v3
 v4
 Tiết 1 Tiết 2 Tiết 3 Tiết 4
 v1 và v3 v2 và v4 v5 v6
 5 / 44
Xếp lịch học
 ▶ Ta tìm cách phân hoạch tập đỉnh thành 4 phần sao cho không
 phần nào chứa cặp đỉnh kề nhau.
 ▶ Một cách hình thức, đây là một hàm
 c : {v1, v2, v3, v4, v5, v6} −→ {1, 2, 3, 4}
 gán mỗi đỉnh với một giờ học.
 ▶ Không mất tổng quát ta dùng các số nguyên dương cho các
 màu.
 6 / 44
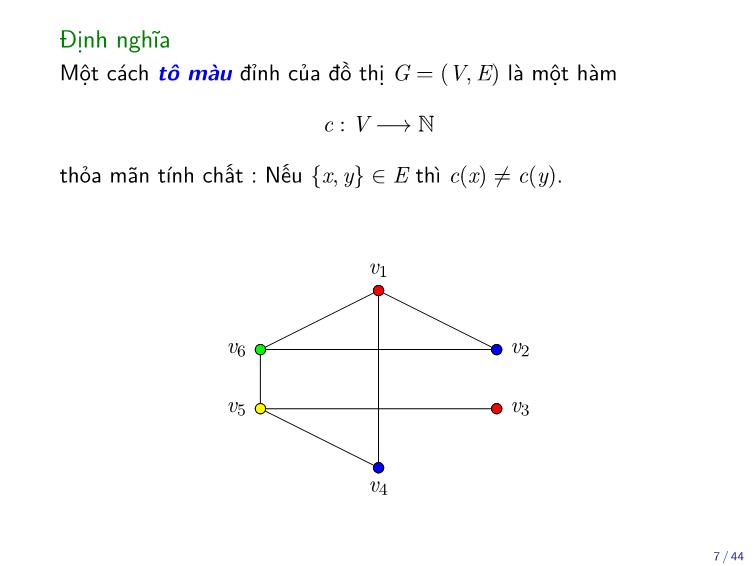
Định nghĩa
Một cách tô màu đỉnh của đồ thị G = (V, E) là một hàm
 c : V −→ N
thỏa mãn tính chất : Nếu {x, y} ∈ E thì c(x) ≠ c(y).
 v1
 v6 v2
 v5 v3
 v4
 7 / 44
 Định nghĩa
 Sắc số của đồ thị G, ký hiệu là χ(G), là số nguyên k nhỏ nhất
 thỏa mãn có một cách tô màu G dùng k màu.
 Nói cách khác, χ(G) = k nếu và chỉ nếu có một cách tô màu c từ
V tới tập {1, 2,..., k}, và k là số nguyên nhỏ nhất thỏa mãn tính
 chất này.
 Ví dụ
 v1
 v6 v2
 Tìm sắc số của đồ thị
 v5 v3
 v4
 8 / 44
Tìm số màu
 Để chứng minh rằng sắc số của một đồ thị là k thì ta phải:
 1. tìm một cách tô màu dùng k màu;
 2. chứng minh rằng không có cách tô màu nào dùng ít hơn k
 màu.
 9 / 44
 Bài tập
 Tìm sắc số của các đồ thị sau:
 (i) đồ thị đầy đủ Kn;
 (ii) đồ thị vòng C2r;
(iii) đồ thị vòng C2r+1;
 10 / 44
Bài tập
Tìm sắc số của các đồ thị sau:
 11 / 44
Bài tập
Hãy mô tả tất cả các đồ thị G có χ(G) = 1.
 12 / 44
Nội dung
 Định nghĩa và ví dụ
 Thuật toán tham lam tô màu đỉnh
 Đồ thị hai phần
 Bài tập
Bài toán
Cho đồ thị G. Hãy tìm χ(G).
là bài toán khó. Người ta chưa biết thuật toán “nhanh” nào để
giải nó, và hầu hết mọi người đều tin rằng không có thuật toán
như vậy.
 14 / 44
Thuật toán tham lam
1. Sắp thứ tự các đỉnh theo thứ tự nào đó: v1, v2, ··· , vn.
2. for i = 1, 2,..., n :
3. Gán màu hợp lệ nhỏ nhất cho vi.
 15 / 44
Bài tập
Dùng thuật toán tham lam để tô màu đồ thị sau:
 v1
 v6 v2
 v5 v3
 v4
 16 / 44
Bài tập
Tìm một cách sắp thứ tự các đỉnh để thuật toán tham lam tô màu
đồ thị sau dùng ít màu nhất có thể.
 17 / 44
Bài tập
Tìm một cách sắp thứ tự các đỉnh để thuật toán tham lam tô màu
đồ thị sau dùng ít màu nhất có thể.
 18 / 44
Mệnh đề
Nếu mọi đỉnh trong G đều có bậc ≤ k, thì thuật toán tham lam
dùng nhiều nhất k + 1 màu.
Thử chứng minh bằng quy nạp theo k
Đặt P(k) = “nếu mọi đỉnh trong G đều có bậc ≤ k thì thuật toán
tham lam dùng nhiều nhất k + 1 màu”
Bước cơ sở : P(0) đúng. Tại sao?
Bước quy nạp : Giả sử P(k) đúng để chứng minh P(k + 1) !!!
 19 / 44
Chứng minh bằng quy nạp theo số đỉnh
 Đặt P(n) = “Đồ thị G với n đỉnh và bậc mọi đỉnh trong G đều
 ≤ k thì thuật toán tham lam dùng nhiều nhất k + 1 màu.”
 Bước cơ sở : P(1) đúng vì G không có cạnh nào.
 Bước quy nạp : Giả sử P(n) đúng để chứng minh P(n + 1).
 ▶ Xét G là đồ thị bất kỳ với n + 1 đỉnh và có bậc lớn nhất ≤ k.
 ▶
 Sắp xếp các đỉnh theo thứ tự nào đó: v1, v2,..., vn, vn+1.
 ▶ ′
 Xóa đỉnh vn+1 khỏi G ta thu được đồ thị G .
 ▶ Đồ thị G′ cũng có bậc lớn nhất ≤ k. Tại sao?
 ▶ Theo quy nạp, thuật toán tham lam tô màu G′ dùng nhiều
 nhất k + 1 màu.
 20 / 44
Chứng minh (tiếp)
 u1
 u2
 v . ≤
 n+1 . vn+1 có ℓ k hàng xóm
 uℓ
 ▶ ′
 Thêm đỉnh vn+1 và các cạnh liên quan vào lại G để được G.
 ▶
 Đỉnh vn+1 có ≤ k hàng xóm. Tại sao?
 ▶ Vậy tồn tại một màu hợp lệ trong {1, 2,..., k + 1} để tô cho
 vn+1.
 ▶ Vậy thuật toán tham lam tô màu G dùng không quá k + 1
 màu. 
 21 / 44
Bài tập
Một đồ thị có độ rộng k − 1 nếu các đỉnh có nó có thể được sắp
xếp thành dãy
 v1, v2, ··· , vn
sao cho mỗi đỉnh vi có cạnh nối với nhiều nhất k − 1 đỉnh đứng
trước nó.
Hãy dùng quy nạp để chứng minh rằng mọi đồ thị với độ rộng nhỏ
hơn hoặc bằng k − 1 đều có thể tô bằng k màu.
 22 / 44
Mệnh đề
Cho G là đồ thị với mọi đỉnh đều có bậc ≤ k. Nếu G liên thông và
không chính quy, vậy thì χ(G) ≤ k.
 Hình: Đồ thị này có độ rộng 2. Tại sao?
 23 / 44
Mệnh đề
Cho G là đồ thị với mọi đỉnh đều có bậc ≤ k. Nếu G liên thông và
không chính quy, vậy thì χ(G) ≤ k.
Ý tưởng chứng minh
Ta tìm một cách sắp thứ tự
 v1, v2, ··· , vn
cho các đỉnh để thuật toán tham lam tô màu cho G dùng không
quá k màu.
 24 / 44
Sắp thứ tự các đỉnh
 ▶
 Chọn một đỉnh trong G có bậc ≤ k − 1. Gán nó là vn.
 ▶
 Liệt kê cho các hàng xóm của vn theo thứ tự là:
 vn−1, vn−2, ··· , vn−r.
 ▶
 Liệt kê các hàng xóm của vn−1 (trừ vn). Có ≤ k − 1 đỉnh.
 ▶
 Liệt kê các hàng xóm của vn−2 chưa được liệt kê. Có ≤ k − 1
 đỉnh.
 ▶ Và cứ thế đến khi mọi đỉnh của G được liệt kê. (do G liên
 thông)
 25 / 44
Ví dụ
 v5
 v4 v6
 v2 v1
 v3
 26 / 44
Khẳng định
Với cách sắp xếp thứ tự đỉnh v1, v2,..., vn như trên, mỗi đỉnh vi
chỉ nối với nhiều nhất k − 1 đỉnh đứng trước nó.
Có nghĩa rằng đồ thị này có độ rộng k − 1.
 27 / 44
Định lý
Nếu G là đồ thị với mọi đỉnh đều có bậc ≤ k, thì
 (i) χ(G) ≤ k + 1;
(ii) nếu G liên thông và không chính quy, thì χ(G) ≤ k.
 28 / 44
Nội dung
 Định nghĩa và ví dụ
 Thuật toán tham lam tô màu đỉnh
 Đồ thị hai phần
 Bài tập
Định nghĩa
Đồ thị G là đồ thị hai phần nếu χ(G) ≤ 2.
 Khi đó tập đỉnh V của G
 được phân hoạch thành hai
 phần
 V = Vđỏ ∪ Vxanh
 30 / 44
Ví dụ
Đồ thị sau có phải đồ thị hai phần không?
 31 / 44
Định lý
G là đồ thị hai phần nếu và chỉ nếu nó không chứa chu trình độ
dài lẻ.
 32 / 44
Chứng minh
 Nếu G có chu trình độ dài lẻ
 
 Mâu thuẫn với tính chất χ(G) ≤ 2.
 33 / 44
Chứng minh (tiếp)
 Ngược lại, giả sử G không có chu trình độ dài lẻ. Ta xây dựng một
 thứ tự cho các đỉnh của G để thuật toán tham lam tô G bằng hai
 màu.
 Sắp thứ tự các đỉnh
 ▶
 Chọn một đỉnh bất kỳ gọi là v1; ta nói rằng v1 có mức 0.
 ▶
 Liệt kê các hàng xóm của v1, gọi chúng là v2, v3,..., vr; ta
 nói rằng các đỉnh này có mức 1.
 ▶
 Liệt kê các hàng xóm của các đỉnh ở mức 1 (trừ v1); ta nói
 rằng các đỉnh này có mức 2.
 ▶ Cứ thế tiếp tục, ta liệt kê ở mức ℓ các đỉnh là hàng xóm của
 mức ℓ − 1, ngoại trừ những đỉnh đã liệt kê ở mức ℓ − 2.
 ▶ Khi không còn đỉnh nào được thêm vào, ta đã sắp thứ tự cho
 cho các đỉnh trong một thành phần liên thông G0 của G. Ta
 tiếp tục như vậy với thành phần liên thông tiếp theo.
 34 / 44
Ví dụ
Đồ thị dưới đây có thể tô bằng hai màu: các đỉnh có mức chẵn
được tô màu đỏ, các đỉnh có mức lẻ được tô màu xanh.
 1 0
 2 1
 3 2
 2 1
 35 / 44
Chứng minh (tiếp)
 ▶ Các đỉnh mức ℓ chỉ nối với đỉnh mức ℓ − 1 hoặc ℓ + 1.
 ▶ Các đỉnh mức ℓ không nối với nhau; ngược lại đồ thị sẽ có
 chu trình độ dài lẻ.
 z
 
 u v
 ▶ Với cách sắp thứ tự các đỉnh như vậy, thuật toán tô màu sẽ
 chỉ dùng hai màu: các đỉnh có mức chẵn được tô màu đỏ, các
 đỉnh có mức lẻ được tô màu xanh.
 36 / 44
Nội dung
 Định nghĩa và ví dụ
 Thuật toán tham lam tô màu đỉnh
 Đồ thị hai phần
 Bài tập
Bài tập
Tìm 3 cách đánh số thứ tự các đỉnh của đồ thị lập phương dưới
đây để thuật toán tham lam dùng 2, 3, và 4 màu.
 38 / 44
Bài tập
Chứng minh rằng với mọi đồ thị G ta luôn có cách sắp thứ tự các
đỉnh để thuật toán tham lam tô màu G dùng đúng χ(G) màu.
[Gợi ý: dùng một cách tô màu dùng χ(G) màu để xác định thứ tự
đỉnh cho thuật toán tham lam.]
 39 / 44
Bài tập
Có sáu trạm phát sóng radio A, B, C, D, E, F với khoảng cách giữa
các trạm (tính theo dặm) được cho bởi bảng sau
 ABCDEF
 A - 85 175 100 50 100
 B 85 - 125 175 100 130
 C 175 125 - 100 200 250
 D 100 175 100 - 210 220
 E 50 100 200 210 - 100
 F 100 130 250 220 100 -
Giả sử những trạm phát ở cách nhau ít hơn 150 dặm phải phát ở
tần số khác nhau. Hãy tìm cách gán tần số cho mỗi trạm để số tần
số là ít nhất.
 40 / 44
Bài tập
Viện CNTT&TT lên lịch bảo vệ khóa luận cho sinh viên K56. Các
giáo sư A, B,..., J sẽ là thành viên của 8 hội đồng bảo vệ dưới
đây:
 Hội đồng 1 : ABCD 5 : AHJ
 2 : ACDE 6 : HIJ
 3 : BDFG 7 : GHJ
 4 : CDFG 8 : EI
Thời gian bảo vệ của mỗi hội đồng là một ngày. Hai hội đồng có
thể bảo vệ cùng ngày nếu không có chung thành viên. Hãy tìm
số ngày ít nhất để tất cả các hội đồng có thể bảo vệ xong. Giải
thích câu trả lời của bạn.
 41 / 44
Số hội đồng bảo vệ
 ▶ Xét đồ thị với tập đỉnh là
 các hội đồng, giữa hai dỉnh 7
 có cạnh nối nếu hai hội 5 6
 đồng có chung thành viên.
 ▶ Bài toán tương đương với
 bài toán tìm số màu ít nhất 2 8
 để tô đồ thị này.
 ▶ Đồ thị này có chứa clique
 {1, 2, 3, 4} có kích thước 4 1 3
 nên số ngày bằng 4 là ít 4
 nhất có thể.
 42 / 44
Bài tập
Ký hiệu ei(G) là số đỉnh của đồ thị G có bậc lớn hơn i. Dùng
thuật toán tham lam để chỉ ra rằng nếu tồn tại i để ei(G) ≤ i + 1
thì χ(G) ≤ i + 1.
 43 / 44
 Bài tập
 Đồ thị Mr (r ≥ 2) đạt được từ đồ thị chu trình C2r bằng cách
 thêm các cạnh nối giữa mỗi cặp đỉnh đối nhau. Chứng minh rằng
 (i) Mr là đồ thị hai phần khi r là số lẻ.
 (ii) χ(Mr) = 3 khi r chẵn và r ≠ 2.
(iii) χ(M2) = 4.
 44 / 44