Bài giảng Toán rời rạc - Chương: Quy hoạch động - Trần Vĩnh Đức
Đường đi ngắn nhất trên DAG
this helps with shortest paths, suppose we want to figure out distances from node S to the
other nodes. For concreteness, let’s focus on node D. The only way to get to it is through its
Figure 6.1 A dag and its linearization (topological ordering).
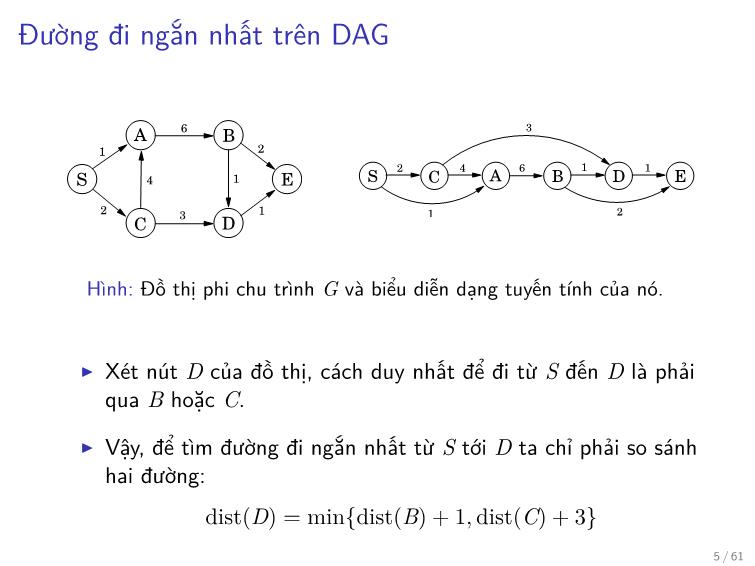
Hình: Đồ thị phi chu trình G và biểu diễn dạng tuyến tính của nó. 169
▶ Xét nút D của đồ thị, cách duy nhất để đi từ S đến D là phải
qua B hoặc C.
▶ Vậy, để tìm đường đi ngắn nhất từ S tới D ta chỉ phải so sánh
hai đường:
dist(D) = minfdist(B) + 1; dist(C) + 3g

Trang 1

Trang 2

Trang 3

Trang 4
Trang 5
Trang 6
Trang 7
Trang 8

Trang 9

Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Toán rời rạc - Chương: Quy hoạch động - Trần Vĩnh Đức", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Toán rời rạc - Chương: Quy hoạch động - Trần Vĩnh Đức

ccordingly.
Here is the Floyd-Warshalldist(i,algorithm—andk, k−1) + distas(k,youj, k−can1)see< ,distit takes(i, j,Ok(−V1)3,) time.
| |
for i = 1 to n:
for j = 1 to n: 49 / 61
dist(i, j, 0) =
∞
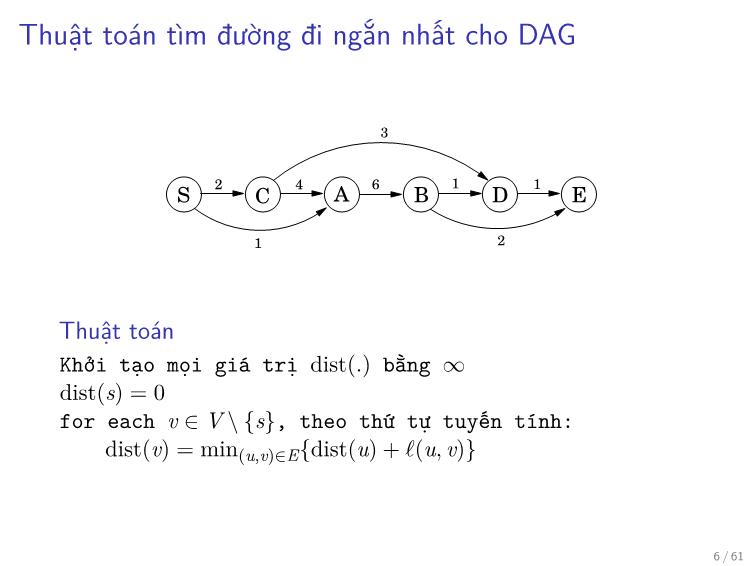
Thuật toán quy hoạch động
for i = 1 to n:
for j = 1 to n:
dist(i, j, 0) = ∞
for all (i, j) ∈ E:
dist(i, j, 0) = ℓ(i, j)
for k = 1 to n:
for i = 1 to n:
for j = 1 to n:
{
dist(i, k, k−1) + dist(k, j, k−1),
dist(i, j, k) = min
dist(i, j, k−1)
50 / 61
186 Algorithms
FigureBài6.8 W toáne want ngườia path bánfrom s hàngto t that duis lịchboth short and has few edges.
A 2 B
1 4
5 1
S 5 T
2 1
C 3 D
▶ Một người bán hàng thích du lịch đang sẵn sàng cho một
6.6 Shortestchuyếnpaths đi bán hàng.
▶ Bắt đầu từ nhà, với chiếc vali trong tay, anh sẽ đi một hành
We started this chapter with a dynamic programming algorithm for the elementary task of
trình trong đó mỗi thành phố cần đến sẽ được thăm đúng
the shortestfindingpath in a dag. toWmoree nowsophisticatedturn shortest-path problems
and see how thesemộttoo lầncan trướcbe accommodated khi quay về nhà.by our powerful algorithmic technique.
▶
Cho khoảng cách dij giữa mỗi cặp thành phố i và j, anh ta
Shortest reliablenênpaths thăm các thành phố theo thứ tự nào để tối ưu tổng
khoảng cách?
Life is complicated, andsuchabstractionsas graphs, edge lengths, and shortest paths rarely
the wholecapturetruth. In a communicationsnetwork, for example, even if edge51 / 61lengths
faithfully reflect transmission delays, there may be other considerations involved in choosing
a path. For instance, each extra edge in the path might be an extra “hop” fraught with uncer-
tainties and dangers of packet loss. In such cases, we would like to avoid paths with too many
edges. Figure 6.8 illustrates this problem with a graph in which the shortest path from S to
T has four edges, while there is another path that is a little longer but uses only two edges. If
four edges translate to prohibitive unreliability, we may have to choose the latter path.
Suppose then that we are given a graph G with lengths on the edges, along with two nodes
s and t and an integer k, and we want the shortest path from s to t that uses at most k edges.
Is there a quick way to adapt Dijkstra’s algorithm to this new task? Not quite: that
algorithm focuses on the length of each shortest path without “remembering” the number of
hops in the path, which is now a crucial piece of information.
In dynamic programming, the trick is to choose subproblems so that all vital information
is remembered and carried forward. In this case, let us define, for each vertex v and each
integer i k, dist(v, i) to be the length of the shortest path from s to v that uses i edges. The
≤
starting values dist(v, 0) are for all vertices except s, for which it is 0. And the general
∞
update equation is, naturally enough,
dist(v, i) = min dist(u, i 1) + ℓ(u, v) .
(u,v) E{ − }
∈
Need we say more?
186 Bài tập Algorithms
Người bán hàng nên thăm các thành phố theo thứ tự nào để tối
Figure 6.8 Wưue w tổngant khoảnga path from cách?s to t that is both short and has few edges.
A 2 B
1 4
5 1
S 5 T
2 1
C 3 D
6.6 Shortest paths
We started this chapter with a dynamic programming algorithm for the elementary task of
the shortestfindingpath in a dag. toWmoree nowsophisticatedturn 52 / 61 shortest-path problems
and see how these too can be accommodated by our powerful algorithmic technique.
Shortest reliable paths
Life is complicated, andsuchabstractionsas graphs, edge lengths, and shortest paths rarely
the wholecapturetruth. In a communicationsnetwork, for example, even if edge lengths
faithfully reflect transmission delays, there may be other considerations involved in choosing
a path. For instance, each extra edge in the path might be an extra “hop” fraught with uncer-
tainties and dangers of packet loss. In such cases, we would like to avoid paths with too many
edges. Figure 6.8 illustrates this problem with a graph in which the shortest path from S to
T has four edges, while there is another path that is a little longer but uses only two edges. If
four edges translate to prohibitive unreliability, we may have to choose the latter path.
Suppose then that we are given a graph G with lengths on the edges, along with two nodes
s and t and an integer k, and we want the shortest path from s to t that uses at most k edges.
Is there a quick way to adapt Dijkstra’s algorithm to this new task? Not quite: that
algorithm focuses on the length of each shortest path without “remembering” the number of
hops in the path, which is now a crucial piece of information.
In dynamic programming, the trick is to choose subproblems so that all vital information
is remembered and carried forward. In this case, let us define, for each vertex v and each
integer i k, dist(v, i) to be the length of the shortest path from s to v that uses i edges. The
≤
starting values dist(v, 0) are for all vertices except s, for which it is 0. And the general
∞
update equation is, naturally enough,
dist(v, i) = min dist(u, i 1) + ℓ(u, v) .
(u,v) E{ − }
∈
Need we say more?
186 Algorithms
Bài toán con
Figure 6.8 We want a path from s to t that is both short and has few edges.
A 2 B
1 4
5 1
S 5 T
2 1
C 3 D
6.6 Shortest pathsVới mỗi tập con các thành phố S = {1, 2,..., n} có
chứa 1, và j ∈ S, ta ký hiệu C(S, j) là độ dài của đường
We started this cđihapter ngắnwith nhấta thămdynamic mỗi đỉnhprogramming của S đúngalgorithm một lần,for bắtthe đầuelementary task of
the shortestfindingpath in a dag. toWmoree nowsophisticatedturn shortest-path problems
and see how thesetừtoo1 vàcan kếtbe thúcaccommodated tại j. by our powerful algorithmic technique.
Shortest reliable paths
53 / 61
Life is complicated, andsuchabstractionsas graphs, edge lengths, and shortest paths rarely
the wholecapturetruth. In a communicationsnetwork, for example, even if edge lengths
faithfully reflect transmission delays, there may be other considerations involved in choosing
a path. For instance, each extra edge in the path might be an extra “hop” fraught with uncer-
tainties and dangers of packet loss. In such cases, we would like to avoid paths with too many
edges. Figure 6.8 illustrates this problem with a graph in which the shortest path from S to
T has four edges, while there is another path that is a little longer but uses only two edges. If
four edges translate to prohibitive unreliability, we may have to choose the latter path.
Suppose then that we are given a graph G with lengths on the edges, along with two nodes
s and t and an integer k, and we want the shortest path from s to t that uses at most k edges.
Is there a quick way to adapt Dijkstra’s algorithm to this new task? Not quite: that
algorithm focuses on the length of each shortest path without “remembering” the number of
hops in the path, which is now a crucial piece of information.
In dynamic programming, the trick is to choose subproblems so that all vital information
is remembered and carried forward. In this case, let us define, for each vertex v and each
integer i k, dist(v, i) to be the length of the shortest path from s to v that uses i edges. The
≤
starting values dist(v, 0) are for all vertices except s, for which it is 0. And the general
∞
update equation is, naturally enough,
dist(v, i) = min dist(u, i 1) + ℓ(u, v) .
(u,v) E{ − }
∈
Need we say more?
Đưa về bài toán nhỏ hơn
▶ Nếu ta bắt đầu tại 1 và kết thúc tại j; ta nên chọn đến đỉnh
nào trước khi đến j?
▶ Đỉnh này sẽ là một đỉnh i ∈ S thỏa mãn: độ dài đường đi
ngắn nhất từ 1 đến i cộng với dij là nhỏ nhất.
C(S, j) = min C(S − {j}, i) + dij
i∈S:i≠ j
▶ Khi |S| > 1, ta ký hiệu C(S, 1) = ∞ vì đường đi không thể
vừa bắt đầu và kết thúc ở 1.
54 / 61
Thuật toán quy hoạch động
C({1}, 1) = 0
for s = 2 to n:
for all tập con S ⊆ {1, 2,..., n} thỏa mãn |S| = s và
1 ∈ S:
C(S, 1) = ∞
for all j ∈ S, j ≠ 1:
C(S, j) = min{C(S − {j}, i) + dij : i ∈ S, i ≠ j}
return minj C({1,..., n}, j) + dj1
Có nhiều nhất 2n · n bài toán con, và mỗi bài mất thời gian tuyến
tính để giải. Độ phức tạp là O(n2 · 2n).
55 / 61
Nội dung
Đường đi ngắn nhất trên DAG
Dãy con tăng dài nhất
Khoảng cách soạn thảo
Bài toán cái túi
Nhân nhiều ma trận
Đường đi ngắn nhất
Tập độc lập trên cây
Tập độc lập
Định nghĩa
S. Dasgupta,MộtC tập.H. P conapadimitriou, các đỉnh Sand⊆ UV.Vlà. V mộtaziranitập độc lập của đồ thị 191
G = (V, E) nếu không có cạnh giữa chúng.
Figure 6.10 The largest independent set in this graph has size 3.
1 2
5 6
3 4
Figure 6.11▶ I{(u1), 5is}thelà mộtsize of tậpthe độclargest lập, nhưngindependent{1, 4,set5} ofkhôngthe subtree phải. rooted at u. Two
cases: either u is in this independent set, or it isn’t.
▶ Tập độc lập lớn nhất là {2, 3, 6}.
r
57 / 61
u
Exercises
6.1. A contiguous subsequence of a list S is a subsequence made up of consecutive elements of S. For
instance, if S is
5, 15, 30, 10, 5, 40, 10,
− −
then 15, 30, 10 is a contiguous subsequence but 5, 15, 40 is not. Give a linear-time algorithm for
−
the following task:
Input: A list of numbers, a1, a2, . . . , an.
Output: The contiguous subsequence of maximum sum (a subsequence of length zero
has sum zero).
For the preceding example, the answer would be 10, 5, 40, 10, with a sum of 55.
−
(Hint: For each j 1, 2, . . . , n , consider contiguous subsequences ending exactly at position j.)
∈ { }
6.2. You are going on a long trip. You start on the road at mile post 0. Along the way there are n
hotels, at mile posts a < a < < a , where each a is measured from the starting point. The
1 2 · · · n i
only places you are allowed to stop are at these hotels, but you can choose which of the hotels
you stop at. You must stop at the final hotel (at distance an), which is your destination.
Tập độc lập trên cây
▶ Bài toán tìm tập độc lập lớn nhất được nhiều người tin rằng
không có thuật toán hiệu quả để giải nó.
▶ Nhưng khi đồ thị là một cây thì bài toán có thể giải trong
thời gian tuyến tính.
Bài toán con
Lấy một nút r bất kỳ làm gốc của cây. Mỗi nút u bây giờ sẽ xác
định một cây con gốc u. Ta xét bài toán con:
I(u) = kích thước tập độc lập lớn nhất của cây con gốc u.
Mục đích của ta là tìm I(r).
58 / 61
S. Dasgupta, C.H. Papadimitriou, and U.V. Vazirani 191
Figure 6.10 The largest independent set in this graph has size 3.
1 2
5 6
3 4
FigureĐưa6.11 vềI bài(u) is toánthe size nhỏof the hơnlargest independent set of the subtree rooted at u. Two
cases: either u is in this independent set, or it isn’t.
r
u
Exercises▶ Giả sử ta đã biết tập độc lập lớn nhất của mọi cây con bắt
đầu từ u; tức là ta đã biết I(w) cho mọi con cháu w của u.
6.1. A contiguous subsequence of a list S is a subsequence made up of consecutive elements of S. For
instance▶ Làm, if S is thế nào để tính I(u)?
5, 15, 30, 10, 5, 40, 10,
▶ Tách thành hai trường hợp:− tập− độc lập hoặc chứa u hoặc nó
then 15, 30, 10 is a contiguous subsequence but 5, 15, 40 is not. Give a linear-time algorithm for
không− chứa u.
the following task:
Input: A a , a list,2. . .ofanumbers., , 1 n 59 / 61
Output: The contiguous subsequence of maximum sum (a subsequenceof length zero
has sum zero).
For the preceding example, the answer would be 10, 5, 40, 10, with a sum of 55.
−
(Hint: For each j 1, 2, . . . , n , consider contiguous subsequences ending exactly at position j.)
∈ { }
6.2. You are going on a long trip. You start on the road at mile post 0. Along the way there are n
hotels, at mile posts a < a < < a , where each a is measured from the starting point. The
1 2 · · · n i
only places you are allowed to stop are at these hotels, but you can choose which of the hotels
you stop at. You must stop at the final hotel (at distance an), which is your destination.
S. Dasgupta, C.H. Papadimitriou, and U.V. Vazirani 191
Figure 6.10 The largest independent set in this graph has size 3.
1 2
5 6
3 4
Figure 6.11 I(u) is the size of the largest independent set of the subtree rooted at u. Two
cases:Đưaeither vều bàiis in toánthis independent nhỏ hơnset, or it isn’t.
r
u
Hai trường hợp: tập độc lập hoặc chứa u hoặc nó không chứa u.
Exercises
6.1. A contiguous subsequence of a list S is a subsequence made up of consecutive elements of S. For
instance, if S is { }
5,∑15, 30, 10, 5, 40, 10, ∑
I(u) = max 1 + − I−(w), I(w)
then 15, 30, 10 is a contiguous subsequence but 5, 15, 40 is not. Give a linear-time algorithm for
−
the following task: các cháu w của u các con w của u
Input: A a , a list,2. . .ofanumbers., , 1 n
60 / 61
Output: The contiguous subsequence of maximum sum (a subsequenceof length zero
has sum zero).
For the preceding example, the answer would be 10, 5, 40, 10, with a sum of 55.
−
(Hint: For each j 1, 2, . . . , n , consider contiguous subsequences ending exactly at position j.)
∈ { }
6.2. You are going on a long trip. You start on the road at mile post 0. Along the way there are n
hotels, at mile posts a < a < < a , where each a is measured from the starting point. The
1 2 · · · n i
only places you are allowed to stop are at these hotels, but you can choose which of the hotels
you stop at. You must stop at the final hotel (at distance an), which is your destination.
S. Dasgupta, C.H. Papadimitriou, and U.V. Vazirani 191
Figure 6.10 The largest independent set in this graph has size 3.
1 2
5 6
3 4
FigureĐộ phức6.11 I(u tạp) is the tínhsize toánof the largest independent set of the subtree rooted at u. Two
cases: either u is in this independent set, or it isn’t.
r
u
ExercisesBài tập
Số cây con chính là số đỉnh. Liệu ta có thể cài đặt thuật toán chạy
6.1. A contiguous subsequence of a list S is a subsequence made up of consecutive elements of S. For
instancetrong, if S is
5, 15|, |30, 10|, |5, 40, 10,
O( V− + E−)?
then 15, 30, 10 is a contiguous subsequence but 5, 15, 40 is not. Give a linear-time algorithm for
−
the following task:
61 / 61
Input: A a , a list,2. . .ofanumbers., , 1 n
Output: The contiguous subsequence of maximum sum (a subsequenceof length zero
has sum zero).
For the preceding example, the answer would be 10, 5, 40, 10, with a sum of 55.
−
(Hint: For each j 1, 2, . . . , n , consider contiguous subsequences ending exactly at position j.)
∈ { }
6.2. You are going on a long trip. You start on the road at mile post 0. Along the way there are n
hotels, at mile posts a < a < < a , where each a is measured from the starting point. The
1 2 · · · n i
only places you are allowed to stop are at these hotels, but you can choose which of the hotels
you stop at. You must stop at the final hotel (at distance an), which is your destination.File đính kèm:
 bai_giang_toan_roi_rac_chuong_quy_hoach_dong_tran_vinh_duc.pdf
bai_giang_toan_roi_rac_chuong_quy_hoach_dong_tran_vinh_duc.pdf

