Bài giảng Toán rời rạc - Chương: Luồng trên mạng - Trần Vĩnh Đức

 Luồng trên mạng
 V0.1
 Trần Vĩnh Đức
 HUST
Ngày 20 tháng 11 năm 2019
 1 / 34
Tài liệu tham khảo
 ▶ S. Dasgupta, C. H. Papadimitriou, and U. V. Vazirani,
 Algorithms, July 18, 2006.
 2 / 34
Nội dung
 Bài toán luồng cực đại trên mạng
 Thuật toán Ford-Fulkerson
 Luồng cực đại và lát cắt cực tiểu
 Tính hiệu quả của thuật toán
 Network-flow algorithms 887

 inflow equals outflow
 at every vertex
        con- (except the source
 and the sink)

-

 Local equilibrium in a fow network
0->1->3->5
0->2->4->5
0->1, 2->4, and 3->5
0 to 51
1->43->5
0->2->3->5






- ptg12441863



-

 Bài toán chuyển dầu
tinyFN.txt standard drawing drawing with capacities drawing with fow fow representation
source
V 0 1 2.0 2.0
6 E 0 2 3.0 1.0
8 1 3 3.0 2.0
0 1 2.0 1 4 1.0 0.0
0 2 3.0 2 3 1.0 0.0
1 3 3.0 2 4 1.0 1.0
1 4 1.0 3 5 2.0 2.0
2 3 1.0 4 5 3.0 1.0
2 4 1.0
3 5 2.0
 flow value
4 5 3.0 associated
 with
 each edge
capacities sink
 Anatomy of a network-fow problem
 4 / 34
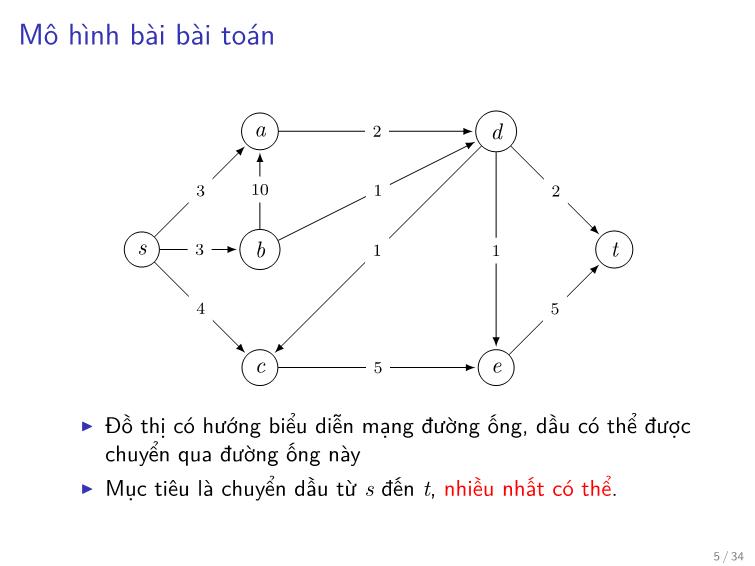
Mô hình bài bài toán
 a 2 d
 3 10 1 2
 s 3 b 1 1 t
 4 5
 c 5 e
 ▶ Đồ thị có hướng biểu diễn mạng đường ống, dầu có thể được
 chuyển qua đường ống này
 ▶ Mục tiêu là chuyển dầu từ s đến t, nhiều nhất có thể.
 5 / 34
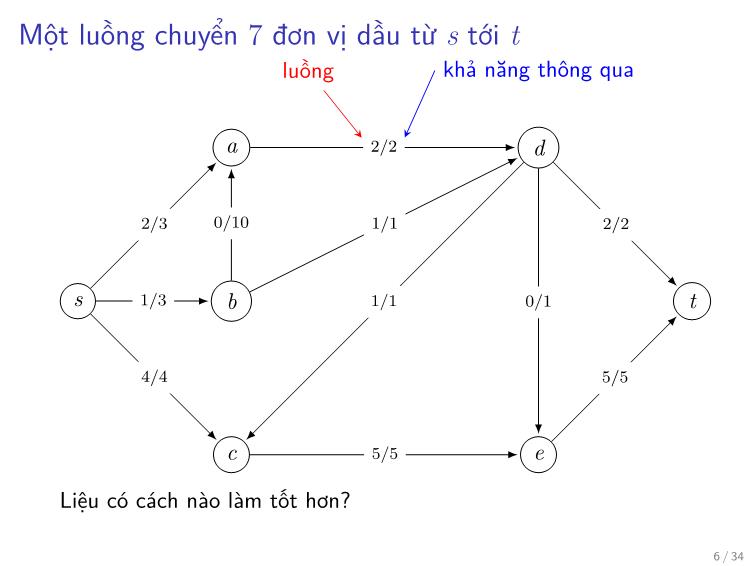
Một luồng chuyển 7 đơn vị dầu từ s tới t
 luồng khả năng thông qua
 a 2/2 d
 2/3 0/10 1/1 2/2
 s 1/3 b 1/1 0/1 t
 4/4 5/5
 c 5/5 e
 Liệu có cách nào làm tốt hơn?
 6 / 34
Mạng
 Định nghĩa
 Một mạng được định nghĩa là bộ G = (V, E, s, t, c), ở đây
 ▶ (V, E) là một đồ thị có hướng;
 ▶ s, t ∈ V, gọi là đỉnh nguồn và đỉnh đích; và
 ▶
 c là một hàm gắn trên mỗi cạnh e của G một giá trị ce > 0
 gọi là khả năng thông qua.
 Bài toán
 Ta muốn chuyển nhiều dầu nhất có thể từ s tới t mà không vượt
 quá khả năng thông qua trên mỗi cạnh.
 7 / 34
Định nghĩa (Luồng)
Một luồng trên mạng G là một hàm
 f : E −→ R+ ∪ {0},
gắn mỗi cạnh e của G với một giá trị số fe, sao cho:
 1. Không vi phạm khả năng thông qua:
 0 ≤ fe ≤ ce với mọi e ∈ E
 2. Với mọi đỉnh u, ngoại trừ s và t, tổng luồng vào u bằng tổng
 luồng ra khỏi u: ∑ ∑
 fwu = fuz.
 (w,u)∈E (u,z)
 Nói cách khác, mạng là bảo toàn (theo luật Kirchhoff).
 8 / 34
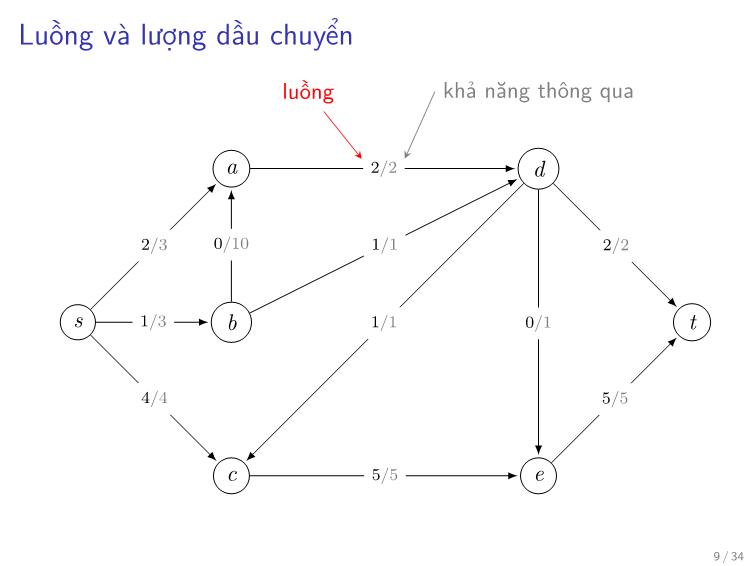
Luồng và lượng dầu chuyển
 luồng khả năng thông qua
 a 2/2 d
 2/3 0/10 1/1 2/2
 s 1/3 b 1/1 0/1 t
 4/4 5/5
 c 5/5 e
 9 / 34
Định nghĩa
Giá trị của luồng là tổng lượng gửi từ s đến t. Theo luật bảo
toàn, size(f) bằng lượng rời khỏi s:
 ∑
 size(f) = fsu.
 (s,u)∈E
 ▶ Mục đích của chúng ta là tìm được luồng có giá trị cực đại.
 ▶ Tương đương, tìm cách gán giá trị
 {fe : e ∈ E}
 thỏa mãn một số ràng buộc.
 ▶ Đây là một bài toán quy hoạch tuyến tính.
 10 / 34
Ví dụ
Bài toán tìm luồng cực đại trong mạng
 a
 1 1
 s 1 t
 1 1
 b
tương đương với bài toán quy hoạch tuyến tính
 max fsa + fsb
 0 ≤ fsa, fsb, fab, fat, fbt ≤ 1
 fsa = fat + fab
 fsb + fab = fbt
 11 / 34
Nội dung
 Bài toán luồng cực đại trên mạng
 Thuật toán Ford-Fulkerson
 Luồng cực đại và lát cắt cực tiểu
 Tính hiệu quả của thuật toán
Thuật toán tham lam
 ▶ Bắt đầu với luồng 0
 ▶ Lặp lại: Chọn một đường đi thích hợp từ s tới t và tăng
 luồng nhiều nhất có thể dọc theo đường này.
 13 / 34
Khởi tạo Tăng luồng
 a a
 0/1 0/1 1/1 1/1
 s 0/1 t s 0/1 t
 0/1 0/1 0/1 0/1
 b b
Tăng luồng Luồng cực đại
 a a
 1/1 1/1 1/1 1/1
 s 0/1 t s 0/1 t
 1/1 1/1 1/1 1/1
 b b
 14 / 34
Khởi tạo Tăng luồng
 a a
 0/1 0/1 1/1 0/1
 s 0/1 t s 1/1 t
 0/1 0/1 0/1 1/1
 b b
Hủy luồng trên cạnh a → b Luồng cực đại
 a a
 1/1 1/1 1/1 1/1
 s 0/1 t s 0/1 t
 1/1 1/1 1/1 1/1
 b b
 15 / 34
Tìm đường tăng luồng
 Tìm cạnh (u, v) có một trong hai kiểu
 ▶
 (u, v) ∈ E và khả năng thông qua cuv vẫn chưa đầy. Khi đó
 fuv có thể tăng thêm nhiều nhất là
 cuv − fuv.
 ▶
 (v, u) ∈ E và có một luồng qua đó, tức là fvu > 0. Khi đó ta
 có thể giảm một phần hoặc toàn bộ fvu.
 16 / 34
Đường tăng luồng
 Cạnh gốc
 Cạnh ngược
 ▶ e = (u, v) ∈ E
 ▶ eR = (v, u)
 ▶ Luồng f
 e ▶
 “Giảm” luồng fe đã gửi
 ▶
 Khả năng ce
 Khả năng thông qua còn lại Ví dụ
 a
 { 1/1 0/1
 c − f nếu e ∈ E s 1/1 t
 cf(e) = e e
 R 0/1 1/1
 fe nếu e ∈ E.
 b
 17 / 34
Đồ thị tăng luồng
 Định nghĩa
 Đồ thị tăng luồng của mạng G với luồng f là đồ thị
 f f
 G = (V, Ef, c ) với
 R
 Ef = {e : fe 0}.
 Ví dụ
 Mạng G với luồng f và đồ thị tăng luồng Gf tương ứng.
 a a
 1/1 0/1 1 1
 s 1/1 t s 1 t
 0/1 1/1 1 1
 b b
 18 / 34
Đường tăng luồng
 Định nghĩa
 ▶ Một đường tăng luồng là một đường đi từ s đến t trong đồ
 thị tăng luồng Gf.
 ▶ Khả năng thông qua của đường tăng luồng P là
 cf(P) = min{cf(e): e ∈ P}
 Augment(f, c, P)
 δ = cf(P)
 foreach cạnh e ∈ P:
 if (e ∈ E) fe = fe + δ
 else f(eR) = f(eR) − δ
 return f
 19 / 34
Thuật toán Ford-Fulkerson
 Ford-Fulkerson (G)
 foreach cạnh e ∈ E: fe = 0
 Gf = đồ thị tăng luồng của G và f
 while (còn đường tăng luồng P trong Gf):
 f = Augment(f, c, P)
 Cập nhật Gf
 return f
 20 / 34
 7. NETWORK FLOW I
 ‣ Ford-Fulkerson demo
 Lecture slides by Kevin Wayne
 Copyright © 2005 Pearson-Addison Wesley
 Copyright © 2013 Kevin Wayne
 Last updated on Sep 8, 2013 6:40 AM
Ford-Fulkerson algorithm demo
 network G flow capacity
 0 / 4
 0 / 10
 0 / 2 0 / 8 0 / 6
 0 / 10 value of flow
 s 0 / 10 0 / 9 0 / 10 t 0
 residual graph Gf
 4
 residual capacity
 10 
 2 8 6
 10 
 s 10 9 10 t
 2
Ford-Fulkerson algorithm demo
network G
 0 / 4
 8
 0 / 10
 —0 / 8
 8 0 / 2 0 / 6
 —0 / 10
 8
 s 0 / 10 0 / 9 —0 / 10 t 0 + 8 = 8
residual graph Gf
 4
 10 
 2 8 6
 10 
 s 10 9 10 t
 3
Ford-Fulkerson algorithm demo
network G
 0 / 4
 0 / 10
 2 —0 / 2 8 / 8 0 / 6
 10
 —8 / 10
 2 2
 s 0 / 10 —0 / 9 —8 / 10 t 8 + 2 = 10
residual graph Gf
 4
 8 10 
 2 8 6
 2
 s 10 9 2 t
 8
 4
Ford-Fulkerson algorithm demo
network G
 0 / 4
 6
 —0 / 10
 2 / 2 8 / 8 6 —0 / 6
 10 / 10
 6 8
 s —0 / 10 —2 / 9 10 / 10 t 10 + 6 = 16
residual graph Gf
 4
 10 
 2 8 6
 10 
 s 10 7 10 t
 2 5
Ford-Fulkerson algorithm demo
network G
 2
 —0 / 4
 8
 —6 / 10
 0 —2 / 2 8 / 8 6 / 6
 10 / 10
 8
 s —6 / 10 8 / 9 10 / 10 t 16 + 2 = 18
residual graph Gf
 4
 6 
 4 
 2 8 6
 10 
 s 4 1 10 t
 6 8 6
Ford-Fulkerson algorithm demo
network G
 3
 —2 / 4
 9
 7
 —8 / 10
 0 / 2 —8 / 8 6 / 6
 10 / 10
 9 9
 s —8 / 10 —8 / 9 10 / 10 t 18 + 1 = 19
 2
residual graph Gf
 2
 8 
 2 
 2 8 6
 10 
 s 2 1 10 t
 8 8 7
 Ford-Fulkerson algorithm demo
 network G
 3 / 4
 9 / 10
 0 / 2 7 / 8 6 / 6
 min cut max flow
 10 / 10
 s 9 / 10 9 / 9 10 / 10 t 19
 3
 residual graph Gf
 1
 9 
 1 
nodes reachable from s 2 7 6
 10 
 1 
 s 1 9 10 t
 9 8
Nội dung
 Bài toán luồng cực đại trên mạng
 Thuật toán Ford-Fulkerson
 Luồng cực đại và lát cắt cực tiểu
 Tính hiệu quả của thuật toán
Phân hoạch L = {s, a, b} và R = {c, d, e, t}
 a 2/2 d
 2/3 0/10 1/1 2/2
 s 1/3 b 1/1 0/1 t
 4/4 5/5
 c 5/5 e
 ▶ Lượng dầu chuyển từ s sang t phải chuyển từ L sang R.
 ▶ Không luồng nào có thể vượt tổng khả năng thông qua của
 các cạnh từ L sang R = 4 + 1 + 2 = 7.
 ▶ Vậy luồng này là tối ưu.
 22 / 34
 
Định nghĩa
 ▶ Một (s, t)-lát cắt (hay ngắn gọn là lát cắt) là một cách phân
 hoạch tập đỉnh thành hai phần L và R sao cho s ∈ L và t ∈ R.
 ▶ Khả năng thông qua của (s, t)-lát cắt là tổng khả năng thông
 qua của các cạnh từ L đến R. Cụ thể,
 ∑
 capacity(L, R) = cuv.
 u∈L, v∈R
Chặn trên cho luồng
Với mỗi luồng f và mỗi lát cắt (L, R), ta luôn có
 size(f) ≤ capacity(L, R).
 23 / 34
Định lý (Max Flow-Min Cut)
Kích thước của luồng cực đại trong mạng bằng với khả năng
thông qua của lát cắt cực tiểu.
Chứng minh.
 ▶ Xét f là luồng tìm được do thuật toán Ford-Fulkerson. Khi đó
 t không đến được từ s trong đồ thị Gf.
 ▶ Xét L là các nút đạt được từ s, và đặt R = V − L. Vậy (L, R)
 là một lát cắt.
 ▶ Ta khẳng định rằng
 size(f) = capacity(L, R).
 ▶ Bởi vì: Mọi cạnh từ L tới R phải đã đầy khả năng thông qua,
 và mọi cạnh từ R tới L phải có luồng bằng 0.
 24 / 34
Định lý (Luồng Nguyên)
Nếu các khả năng thông qua là số nguyên, thì có tồn tại luồng cực
đại nguyên.
Chứng minh.
Thuật toán Ford-Fulkerson kết thúc và luồng cực đại nó tìm được
là luồng nguyên.
 25 / 34
Q&A
Liên quan đến thuật toán Ford-Fulkerson
 ▶ Làm thế nào tính được lát cắt cực tiểu? Dễ thôi, xem chứng
 minh Định lý Max Flow-Min Cut.
 ▶ Làm thế nào để tìm đường tăng luồng? Dùng BFS!
 ▶ Nếu thuật toán kết thúc thì luồng thu được có là luồng cực
 đại? Có chứ. Lát cắt cực tiểu là bằng chứng.
 ▶ Thuật toán có luôn kết thúc? Có, mỗi lần tìm được đường
 tăng luồng là luồng lại tăng lên. Luồng không thể tăng vô hạn.
 26 / 34
Nội dung
 Bài toán luồng cực đại trên mạng
 Thuật toán Ford-Fulkerson
 Luồng cực đại và lát cắt cực tiểu
 Tính hiệu quả của thuật toán
Trường hợp tồi tệ của thuật toán
 Kể cả khi khả năng thông qua là tối ưu, số đường tăng luồng cần
 tìm có thể lớn bằng giá trị của luồng!
 Ví dụ
 Mạng sau có luồng cực đại là 2 × 2100 và thuật toán
 Ford-Fulkerson có thể dùng đến 2 × 2100 đường tăng luồng để tìm
 được luồng cực đại.
 a
 2100 2100
 s 1 t
 2100 2100
 b
 28 / 34
Ví dụ
Khởi tạo và tìm đường tăng luồng đầu tiên
 a
 0/2100 0/2100
 s 0/1 t
 0/2100 0/2100
 b
 29 / 34
Ví dụ
Tìm đường tăng luồng thứ hai
 a
 1/2100 0/2100
 s 1/1 t
 0/2100 1/2100
 b
 30 / 34
Ví dụ
Tìm đường tăng luồng thứ ba
 a
 1/2100 1/2100
 s 0/1 t
 1/2100 1/2100
 b
Tiếp tục 2 × (2100 − 1) lần như vậy, ta được luồng tối ưu.
 31 / 34
Trường hợp tồi tệ của thuật toán
 ▶ Số đường tăng luồng cần tìm có thể lớn bằng giá trị của
 luồng!
 ▶ Tuy nhiên, trường hợp này có thể tránh được nếu lựa chọn
 đường tăng luồng cẩn thận (Ngắn nhất hoặc Đầy nhất).
 Ví dụ
 a
 2100 2100
 s 1 t
 2100 2100
 b
 32 / 34
Lựa chọn đường tăng luồng
 Đường tăng luồng số đường cài đặt
 Đường ngẫu nhiên ≤ mℓ hàng đợi ngẫu nhiên
 Đường DFS ≤ mℓ ngăn xếp (DFS)
 Đường ngắn nhất ≤ 1/2mn hàng đợi (BFS)
 Đường đầy nhất ≤ m ln(mℓ) hàng đợi ưu tiên
 Bẳng: Đồ thị có trọng số với n đỉnh và m cạnh, và các khả năng thông
 qua là số nguyên trong khoảng 1 đến ℓ
 33 / 34
Bài tập
Hãy chạy thuật toán Ford-Fulkerson để tìm luồng cực đại cho
mạng sau. Bạn nên dùng thuật toán BFS để tìm đường tăng luồng.
 a 2 d
 3 10 1 2
 s 3 b 1 1 t
 4 5
 c 5 e
 34 / 34