Bài giảng Toán rời rạc - Chương: Kỹ thuật Hàm sinh - Trần Vĩnh Đức
Bài tập
▶ Ta cần $15 để đóng góp cứu trợ đồng bào vùng bão lụt.
▶ Có 20 sinh viên tham gia đóng góp.
▶ Biết rằng 19 người đầu tiên sẽ góp $1 hoặc không, người
thứ 20 sẽ góp $1 hoặc $5 (hoặc không góp).
▶ Hãy dùng hàm sinh để tính số cách quyên góp $15.

Trang 1

Trang 2

Trang 3
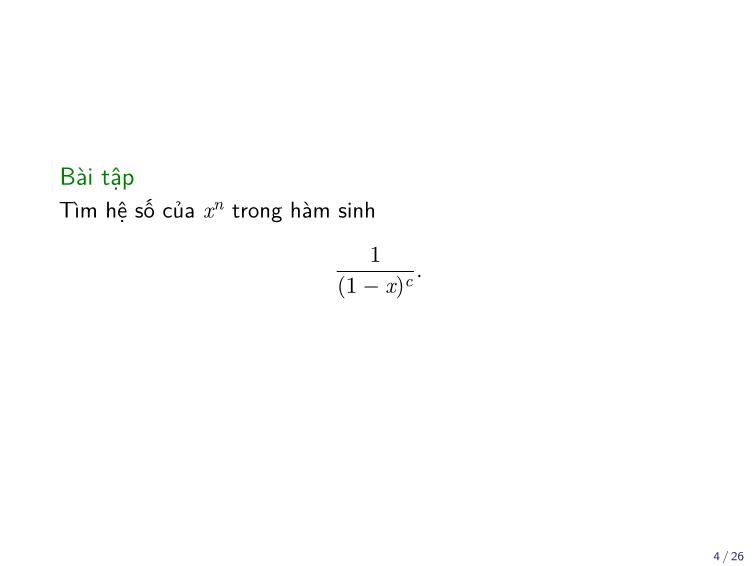
Trang 4

Trang 5

Trang 6

Trang 7

Trang 8

Trang 9

Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Toán rời rạc - Chương: Kỹ thuật Hàm sinh - Trần Vĩnh Đức", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Toán rời rạc - Chương: Kỹ thuật Hàm sinh - Trần Vĩnh Đức

Kỹ thuật Hàm sinh
Trần Vĩnh Đức
HUST
Ngày 24 tháng 7 năm 2018
1 / 26
Nội dung
Tính các hệ số của hàm sinh
Dãy Fibonacci
Định nghĩa
Ta ký hiệu [xn]G(x) là hệ số của xn trong hàm sinh
2
G(x) = g0 + g1x + g2x + ··· .
n
Có nghĩa rằng [x ]G(x) = gn.
3 / 26
Bài tập
Tìm hệ số của xn trong hàm sinh
1
.
(1 − x)c
4 / 26
Lời giải
Ta có
1
= (1 + x + x2 + ··· )c.
(1 − x)c
Hệ số của xn trong hàm sinh trên chính là số nghiệm nguyên
không âm của phương trình
e1 + e2 + ··· + ec = n.
5 / 26
Lời giải (tiếp)
Xét song ánh giữa các nghiệm của phương trình
e1 + e2 + ··· + ec = n
với
”các dãy nhị phân gồm n số 1 và c − 1 số 0”
như sau:
e1 + e2 + ··· + ec = n ⇔ |11{z··· 1} 0 11| {z··· 1} 0 ··· 0 11| {z··· 1}
e1 e2 ec
6 / 26
Lời giải (tiếp)
Theo luật BOOKEEPER thì
”số dãy nhị phân gồm n số 1 và c − 1 số 0”
bằng ( )
n + c − 1 (n + c − 1)!
= .
n n!(c − 1)!
7 / 26
Dãy hệ số tổ hợp
Vậy ta có
⟨ ( ) ( ) ( ) ⟩
c + 1 c + 2 c + 3 1
1, c, , , , ··· ←→ .
2 3 4 (1 − x)c
8 / 26
Bài tập
Tìm hệ số của xn trong hàm sinh
(x2 + x3 + x4 + ··· )5.
Hệ số này chính là số cách chọn n chiếc kẹo từ 5 loại kẹo, mỗi loại
lấy ít nhất hai chiếc.
9 / 26
Bài tập
Tìm hệ số của xn trong hàm sinh
(1 + x)c.
10 / 26
Bài tập
▶ Ta cần $15 để đóng góp cứu trợ đồng bào vùng bão lụt.
▶ Có 20 sinh viên tham gia đóng góp.
▶ Biết rằng 19 người đầu tiên sẽ góp $1 hoặc không, người
thứ 20 sẽ góp $1 hoặc $5 (hoặc không góp).
▶ Hãy dùng hàm sinh để tính số cách quyên góp $15.
11 / 26
Bài tập
Hãy tính số cách để lấy 25 quả bóng giống nhau từ 7 chiếc hộp
biết rằng hộp đầu tiên có không nhiều hơn 10 quả, còn các hộp
khác có số quả tuỳ ý.
12 / 26
Bài tập
Có bao nhiêu cách chọn n quả với các rằng buộc sau?
▶ Số táo phải chẵn.
▶ Số chuối phải chia hết cho 5.
▶ Có nhiều nhất bốn quả cam.
▶ Có nhiều nhất một quả đào.
13 / 26
Ví dụ
Chứng minh đẳng thức sau dùng hàm sinh.
( ) ( ) ( ) ( )
n 2 n 2 n 2 2n
+ + ··· + = .
0 1 n n
14 / 26
Chứng minh.
Hệ số của xn trong hàm sinh F(x) = (1 + x)2n là
( )
2n
.
n
Đặt G(x) = H(x) = (1 + x)n. Vậy hệ số xr trong G(x) = H(x) là
( ) ( )
n n
= .
r n − r
Theo luật tích, hệ số xn trong hàm sinh G(x)H(x) = F(x) là
( )( ) ( )( ) ( )( )
n n n n n n
+ + ··· +
0 n 1 n − 1 n 0
( ) ( ) ( )
n 2 n 2 n 2
= + + ··· +
0 1 n
15 / 26
Nội dung
Tính các hệ số của hàm sinh
Dãy Fibonacci
Dãy Fibonacci
Dãy Fibonacci
⟨0, 1, 1, 2, 3, 5, 8, 13, ···⟩
được định nghĩa bởi
f0 = 0
f1 = 1
fn = fn−1 + fn−2 (với n ≥ 2).
17 / 26
Bài tập
Hãy tìm hàm sinh F(x) cho dãy Fibonacci.
⟨0, 1, f1 + f0, f2 + f1, f3 + f2, ···⟩
18 / 26
Lời giải
⟨ 0, 1, 0, 0, 0, · · · ⟩ ←→ x
⟨ 0, f0, f1, f2, f3, · · · ⟩ ←→ xF(x)
2
+ ⟨ 0, 0, f0, f1, f2, · · · ⟩ ←→ x F(x)
⟨ 0, 1 + f0, f1 + f0, f2 + f1, f3 + f2, ···⟩
Vậy ta có
F(x) = x + xF(x) + x2F(x)
x
= .
1 − x − x2
19 / 26
Bài tập
Hãy viết ra công thức tường minh cho dãy sinh bởi hàm sinh
x
F(x) := .
1 − x − x2
20 / 26
Lời giải
Đầu tiên, ta phân tích mẫu số
2
1 − x − x = (1 − α1x)(1 − α2x).
Ta được
1 √
α = (1 + 5)
1 2
1 √
α = (1 − 5)
2 2
21 / 26
Lời giải (tiếp)
Sau đó, ta tìm A1, A2 thoả mãn
x A1 A2
2 = + .
1 − x − x 1 − α1x 1 − α2x
bằng cách giải hệ phương trình tuyến tính. Ta được
1 1
A1 = = √
α1 − α2 5
−1 1
A2 = = −√
α1 − α2 5
22 / 26
Lời giải (tiếp)
Bây giờ ta đã có
( )
x √1 1 − 1
2 = .
1 − x − x 5 1 − α1x 1 − α2x
Theo công thức hàm sinh ta có
1
2 2 3 3 ···
= 1 + α1x + α1x + α1x +
1 − α1x
1
2 2 3 3 ···
= 1 + α2x + α2x + α2x +
1 − α2x
23 / 26
Lời giải (tiếp)
Vậy thì
( )
1 1 1
F(x) = √ −
5 1 − α1x 1 − α2x
( )
1 2 2 2 2
= √ (1 + α1x + α x + ··· ) − (1 + α2x + α x + ··· )
5 1 2
24 / 26
Lời giải (tiếp)
Cuối cùng ta được công thức lạ cho số Fibonacci thứ n:
n − n
α1 α2
fn = √
((5 ) ( ) )
√ n √ n
1 1 + 5 1 − 5
= √ − .
5 2 2
25 / 26
Phân thức đơn giản
Bổ đề
▶
Xét p(x) là đa thức có bậc nhỏ hơn n với α1, ··· , αn là các
nghiệm khác 0 đôi một phân biệt.
▶
Khi đó tồn tại các hằng số c1, ··· , cn thỏa mãn
p(x) c c
= 1 + ··· + n .
(1 − α1x) ··· (1 − αnx) 1 − α1x 1 − αnx
26 / 26File đính kèm:
 bai_giang_toan_roi_rac_chuong_ky_thuat_ham_sinh_tran_vinh_du.pdf
bai_giang_toan_roi_rac_chuong_ky_thuat_ham_sinh_tran_vinh_du.pdf

