Bài giảng Toán rời rạc - Chương: Ghép cặp trên đồ thị hai phần - Trần Vĩnh Đức

Ghép cặp trên đồ thị hai phần
 Trần Vĩnh Đức
 HUST
 Ngày 24 tháng 7 năm 2018
 1 / 39
Ghép cặp trên đồ thị hai phần
 ▶ Eric Lehman, F Thomson Leighton & Albert R Meyer,
 Mathematics for Computer Science, 2013 (Miễn phí)
 ▶ Albert R Meyer’s slides
 2 / 39
Tìm bạn nhảy
 ▶ Tối thứ bảy, hội sinh viên tổ chức tiệc.
 ▶ Có 300 sinh viên tham gia.
 ▶ Họ không quen hết nhau!
 ▶ Trong 6 người luôn có ba người đôi một quen nhau hoặc ba
 người đôi một lạ nhau!
 3 / 39
Tìm bạn nhảy
 ▶ Tối thứ bảy, hội sinh viên tổ chức tiệc.
 ▶ Có 300 sinh viên tham gia.
 ▶ Họ không quen hết nhau!
 ▶ Nhưng mỗi cô gái quen đúng 50 chàng trai, và mỗi chàng trai
 quen đúng 50 cô gái!
 ▶ Liệu mọi sinh viên có thể nhảy đồng thời sao cho hai người
 nhảy cùng nhau phải biết nhau?
 4 / 39
Nội dung
 Ghép cặp Nam & Nữ
 Định lý Hall
 Làm thế nào để tìm ghép cặp cực đại?
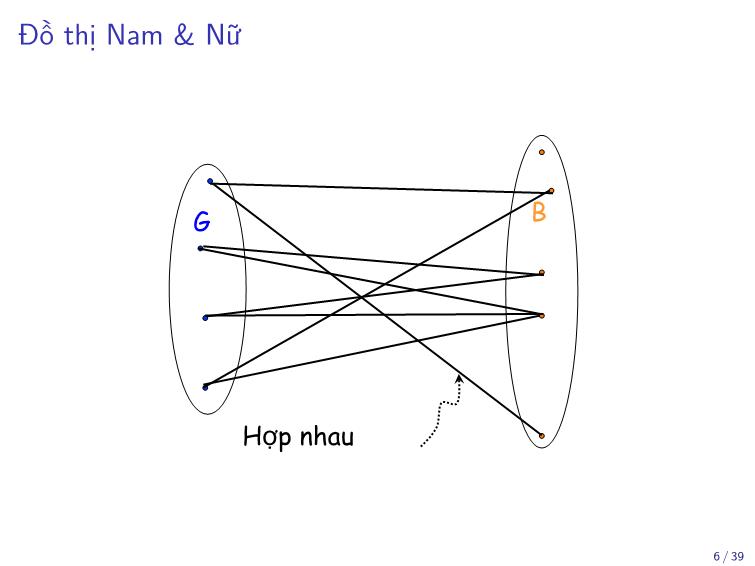
Đồ thị Nam & Nữ
 Nam & Nữ hợp nhau 
 G B 
 Hợp nhau 
 Albert R Meyer. April 3, 2013 bipartite.2 
 6 / 39
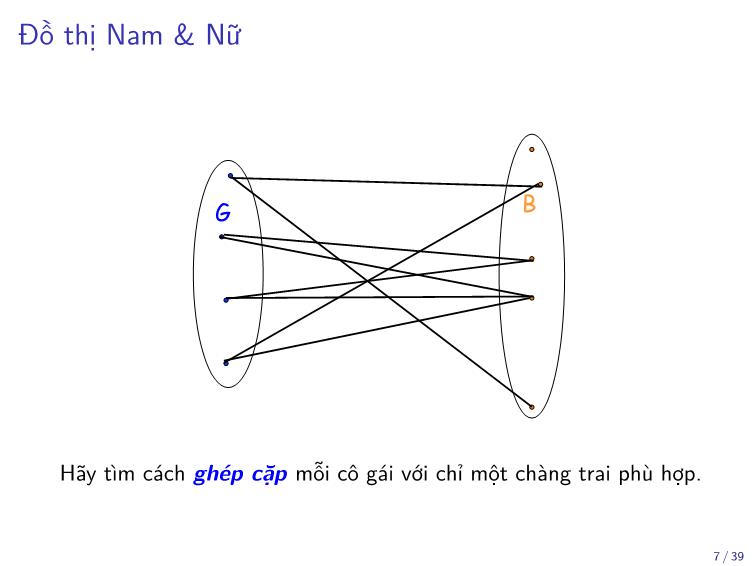
Đồ thị Nam & Nữ
 Compatible Boys & Girls 
 G B 
 Albert R Meyer. April 3, 2013 bipartite.3 
 Hãy tìm cách ghép cặp mỗi cô gái với chỉ một chàng trai phù hợp.
 7 / 39
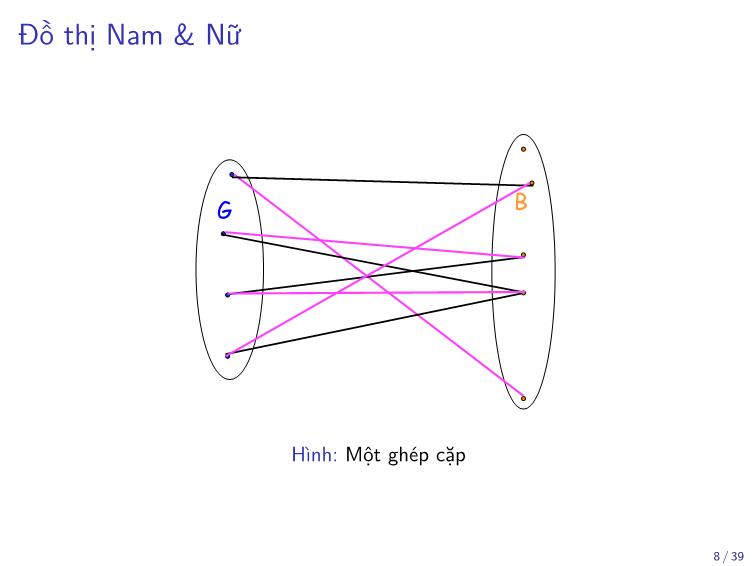
Đồ thị Nam & Nữ
 Compatible Boys & Girls 
 G B 
 Hình:Albert RMột Meyer. April ghép 3, 2013 cặp bipartite.4 
 8 / 39
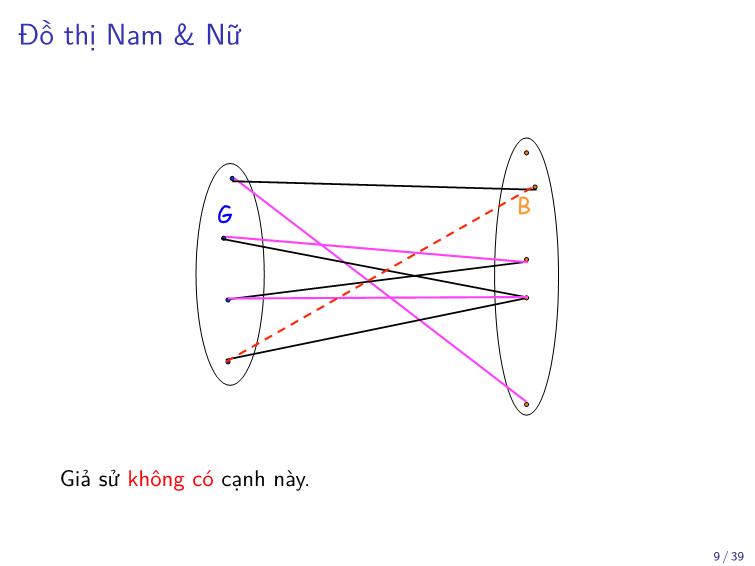
Đồ thị Nam & Nữ
 Compatible Boys & Girls 
 G B 
 suppose this edgeAlbert R Meyer. was April 3, 2013missing bipartite.5 
 Giả sử không có cạnh này.
 9 / 39
Đồ thị Nam & Nữ
 Compatible Boys & Girls 
 G B 
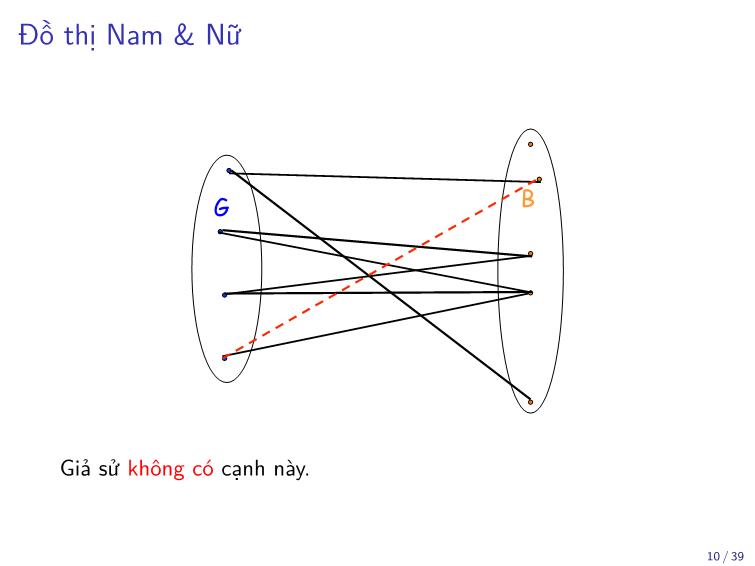
 suppose this edgeAlbert R Meyer. was April 3, 2013missing bipartite.6 
 Giả sử không có cạnh này.
 10 / 39
Đồ thị Nam & Nữ
 Compatible Boys & Girls 
 G B 
 3 
 Albert R Meyer. April 3, 2013 bipartite.7 
 11 / 39
Không đủ số Nam
 NotCompatible enough boysBoys & for Girls these girls! 
 G B 
 3 2 
 3 girls Albert R Meyer.like April 3, 2013 only 2 boysbipartite.8 
 Có 3 cô gái nhưng chỉ có 2 chàng trai phù hợp.
 12 / 39
Không tồn tại cặp ghép cho Nữ
 No match is possible! 
 G B 
 E(S) 
 S3 2 
 Albert R Meyer. April 3, 2013 bipartite.9 
 |S| = 3 > 2 = |E(S)|
 13 / 39
Tắc nghẽn
 No a match bottleneck is possible! 
 G B 
 E(S) 
 S 
 |S| > |E(S)| 
 Albert R Meyer. April 3, 2013 bipartite.10 
 14 / 39
Tắc nghẽn
 ▶ Tắc nghẽn là một tập Nữ S không có đủ số Nam phù hợp.
 E(S) ::= {chàng trai w |
 w kề với ít nhất một cô cái trong S}
 ▶ Tập S là tắc nghẽn
 |S| > |E(S)|
 15 / 39
Bổ đề (Tắc nghẽn)
Nếu tồn tại tắc nghẽn, vậy không tồn tại cặp ghép.
 16 / 39
Định lý (Hall)
Ngược lại, nếu không có tắc nghẽn, vậy có tồn tại cặp ghép.
 17 / 39
114 Matching, marriage and Menger's theorem 
COROLLARY 25.2. Let G = G(V], V2) be a bipartite graph, and for each subset A 
of'V\, let (p(A) be the set of vertices ofVi that are adjacent to at least one vertex of 
A. Then a complete matching from V\ to V2 exists if and only if jAj S l<p(A)/\ for 
each subset A ofV\. 
Proof. The proof of this corollary is a translation into graph terminology of the above 
proof. // 
Exercises 25 
25.1s Suppose that three boys a, b, c know four girls w, x, y, z as in Fig 25.3: 
 boy girls known by boy 
 a w y z 
 b x z 
 c x y 
Fig. 25.3 
 (i) Draw the bipartite graph corresponding to this table of relationships, 
 (ii) Find five different solutions of the corresponding marriage problem, 
 (iii) Check the marriage condition for this problem. 
25.2 A building contractor advertises for a bricklayer, a carpenter, a plumber and a tool-
 maker, and receives five applicants - one for the job of bricklayer, one for carpenter, one 
 for bricklayer and plumber, and two for plumber and toolmaker. 
 Bài(i) tậpDraw the corresponding bipartite graph. 
 (ii) Check whether the marriage condition holds for this problem. 
 Can all of the jobs be filled by qualified people? 
s Tại sao đồ thị dưới đây không có cặp ghép nào phủ tập V1?
25.3 Explain why the graph in Fig. 25.4 has no complete matching from V\ to V 2- When does 
 the marriage condition fail? 
Fig. 25.4 
25.4 (The 'harem problem') Let B be a set of boys, and suppose that each boy in B wishes to 
marry more tha n one of his girl friends. Find a necessary and sufficient condition for the 
 harem problem .t o(Hint have: replaca solution e each boy by several identica18l /copie 39 s of 
 himself, and then use Hall's theorem.) 
Nội dung
 Ghép cặp Nam & Nữ
 Định lý Hall
 Làm thế nào để tìm ghép cặp cực đại?
Đồ thị hai phần H
 Bipartite graph H 
 G B 
 E(H) 
 L(H) R(H) 
 Albert R Meyer. April 3, 2013 Hall.2 
 20 / 39
Ghép cặp hai phía
 Định nghĩa
 Một cặp ghép là một hàm đơn ánh
 m : L(H) −→ R(H)
 thoả mãn: Nếu m(g) = b thì {g, b} là một cạnh của H.
 21 / 39
Định lý (Hall)
Nếu với mọi tập S ⊆ L(H) ta đều có
 |S| ≤ |E(S)|
vậy có tồn tại một cặp ghép.
 22 / 39
Chứng minh định lý Hall
 Bổ đề
 Giả sử không có tắc nghẽn. Hơn nữa, nếu S là một tập những cô
 gái thoả mãn |S| = |E(S)|. Vậy không có tắc nghẽn giữa S và E(S).
 23 / 39
 T Tắc nghẽn 
 s E(S)
 S E(S) 
Vậy S ∪ T là một tắc nghẽn.Albert R Meyer. April 3, 2013 Hall.13 
 24 / 39
Chứng minh định lý Hall
 ▶ Chứng minh bằng quy nạp mạnh theo số Nữ.
 ▶ Nếu chỉ có 1 Nữ. Định lý hiển nhiên đúng.
 ▶ Với số Nữ nhiều hơn 1. Ta xét hai trường hợp.
 25 / 39
Trường hợp 1
 ▶ Có một tập con những cô gái S mà |S| = |E(S)|.
 ▶ Vậy theo bổ đề trước, không có tắc nghẽn trong cả hai đồ thị
 hai phần
 (S, E(S)) và (S, E(S))
 ▶ Theo quy nạp, ta có thể ghép cặp hai đồ thị này riêng biệt. .
 26 / 39
Trường hợp 2
 ▶ Nếu với mọi tập không rỗng những cô gái S ta đều có
 |S| < |E(S)|
 ▶ Chọn lấy một cô gái g. Cô ấy phải hợp với một chàng trai b
 nào đó. Tại sao?
 ▶ Ghép cặp g với b.
 ▶ Loại bỏ g và b.
 ▶ Ta vẫn không có tắc nghẽn đối với các cô gái và chàng trai
 còn lại. Tại sao?
 ▶ Theo quy nạp, ta có thể ghép cặp cho những người còn lại. 
 27 / 39
Kiểm tra tắc nghẽn?
 Mệnh đề
 Nếu mỗi cô gái đều thích ≥ d chàng trai, và mỗi chàng trai đều
 thích ≤ d cô gái, vậy không có tắc nghẽn.
 28 / 39
Chứng minh.
Xét tập các cô gái S và e là số cạnh liên thuộc với S. Ta có
 ∑ ∑
 e = deg(g) ≥ d = d · |S|
 ∈ ∈
 g∑S g S ∑
 e ≤ deg(b) ≤ d = d · |E(S)|
 b∈E(S) b∈E(S)
Vậy ta có
 d · |S| ≤ e ≤ d · |E(S)|.
 Vậy
 |S| ≤ |E(S)|.
 29 / 39
Tìm bạn nhảy
 ▶ Tối thứ bảy, hội sinh viên tổ chức tiệc.
 ▶ Có 300 sinh viên tham gia.
 ▶ Họ không quen hết nhau!
 ▶ Nhưng mỗi cô gái quen đúng 50 chàng trai, và mỗi chàng trai
 quen đúng 50 cô gái!
 ▶ Liệu mọi sinh viên có thể nhảy đồng thời sao cho hai người
 nhảy cùng nhau phải biết nhau?
 30 / 39
Nội dung
 Ghép cặp Nam & Nữ
 Định lý Hall
 Làm thế nào để tìm ghép cặp cực đại?
Đường mở
 Định nghĩa
 Xét đồ thị hai phần G và M là một ghép cặp trong G. Ta nói rằng
 đường đi P là một đường mở (cho M) nếu:
 ▶ P bắt đầu và kết thúc ở hai đỉnh u, v nào đó chưa được ghép
 cặp; và
 ▶ Các cạnh trong P luân phiên thuộc M và không thuộc M.
 32 / 39
 10.4 How to Find a Perfect Matching 173
10.4.1 Show by an example that it may happen that a bipartite graph G has
a perfect matching, but if we are unlucky, the greedy matching M constructed
above is not perfect.
10.4.2 Prove that if G has a perfect matching, then every greedy matching
matches up at least half of the nodes.
So suppose that we have constructed a matching M that is not perfect.
We have to try to increase its size by “backtracking,” i.e., by deleting some
of its edges and replacing them by more edges. But how do we find the
edges we want to replace?
The trick is the following. We look for a path P in G of the following
type: P starts and ends at nodes u and v that are unmatched by M; and
every second edge of P belongs to M (Figure 10.6). Such a path is called
an augmentingTính path. It chất is clear thatcủa an đườngaugmenting pathmởP contains an odd
number of edges, and in fact, the number of its edges not in M is one larger
than the number of its edges in M.
 u v
 ▶ đường mở P chứa một số lẻ
 cạnh.
 ▶ Số cạnh không thuộc M lớn
 hơn 1 so với số cạnh trong M.
 Edges in M Edges in P
 not in M
 33 / 39
 FIGURE 10.6. An augmenting path in a bipartite graph.
Tăng kích thước ghép cặp dùng đường mở
 Hình: Nếu tìm được một đường mở P, ta có thể xóa các cạnh trong M
 và thay bằng các cạnh P không thuộc M.
 34 / 39
Chiến lược tìm ghép cặp cực đại
 1. Bắt đầu với một ghép cặp M bất kỳ (có thể chỉ dùng 1 cạnh).
 2. Tìm một đường mở cho M.
 3. Nếu tìm thấy một đường mở, xây dựng một ghép cặp tốt hơn
 M′.
 4. Nếu không tìm thấy đường mở nào, thì dừng; M là ghép cặp
 cực đại.
 35 / 39
Tại sao chiến lược này đúng?
 Định lý
 Nếu ghép cặp M trong đồ thị hai phần G không phải ghép cặp cực
 đại, thì G chứa một đường mở cho M.
 36 / 39
Chứng minh
 ▶ Xét M∗ là một ghép cặp cực đại;
 ▶ đặt F là tập mọi cạnh thuộc M hoặc M∗, nhưng không thuộc
 cả hai.
 ▶ Tập cạnh F và các đỉnh tạo thành đồ thị với các đỉnh chỉ có
 bậc 1 hoặc 2. Tại sao?
 ▶ Vậy mỗi thành phần liên thông của đồ thị chỉ là đường đi
 hoặc chu trình;
 ▶ và trong mỗi đường đi hoặc chu trình này, các cạnh thuộc M
 luân phiên với các cạnh không thuộc M.
 37 / 39
Chứng minh (tiếp)
 ▶ Vậy thì, trong các chu trình, số cạnh thuộc M bằng với số
 cạnh không thuộc M.
 ▶ Vì |M∗| > |M|, phải có ít nhất một thành phần liên thông là
 đường đi,
 ▶ và đây chính là đường mở.
 38 / 39
9/39 / 39
 10.4 How to Find a Perfect Matching 177
 FIGURE 10.9. A graph for trying out đại. the cực algorithm. cặp ghép là nó minh
 ã ì hpcpccđicocođ h a hnsuv chứng và sau phần hai thị đồ cho cho đại cực cặp ghép tìm Hãy
 10.4.8 Now suppose that we have the weaker condition that every nonempty tập Bài
 subset A on the left has at least A 1 neighbors on the right. Prove that G
 | | −
 contains a matching that matches up all but one node on each side.
 10.4.9 Let G be a bipartite graph with m nodes on both sides. Prove that if
 each node has degree larger than m/2, then it has a perfect matching.
 10.4.10 Does the graph in Figure 10.10 have a perfect matching?
 FIGURE 10.10. A truncated chessboard.
 10.4.11 Draw a graph whose nodes are the subsets of a, b, c , and for which
 { }
 two nodes are adjacent if and only if they are subsets that differ in exactly one
 element.
 (a) What is the number of edges and nodes in this graph? Can you name this
 graph?
 (b) Is this graph connected? Does it have a perfect matching? Does it have a
 Hamilton cycle?