Bài giảng Toán rời rạc - Chương 7. Lý thuyết đồ thị - Bùi Thị Thủy
Lý thuyết đồ thị được khởi đầu từ vài trăm
năm trước (1736 với bài toán 7 cây cầu thành
Konigsberg – Nga, và được gắn với các tên
tuổi lớn như Euler, Gauss, Hamilton.)
Đường một nét Euler, chu trình Hamilton
Tìm đường đi ngắn nhất, Dijkstra
Cây khung nhỏ nhất, Prim, Kruskal
3Định nghĩa đồ thị
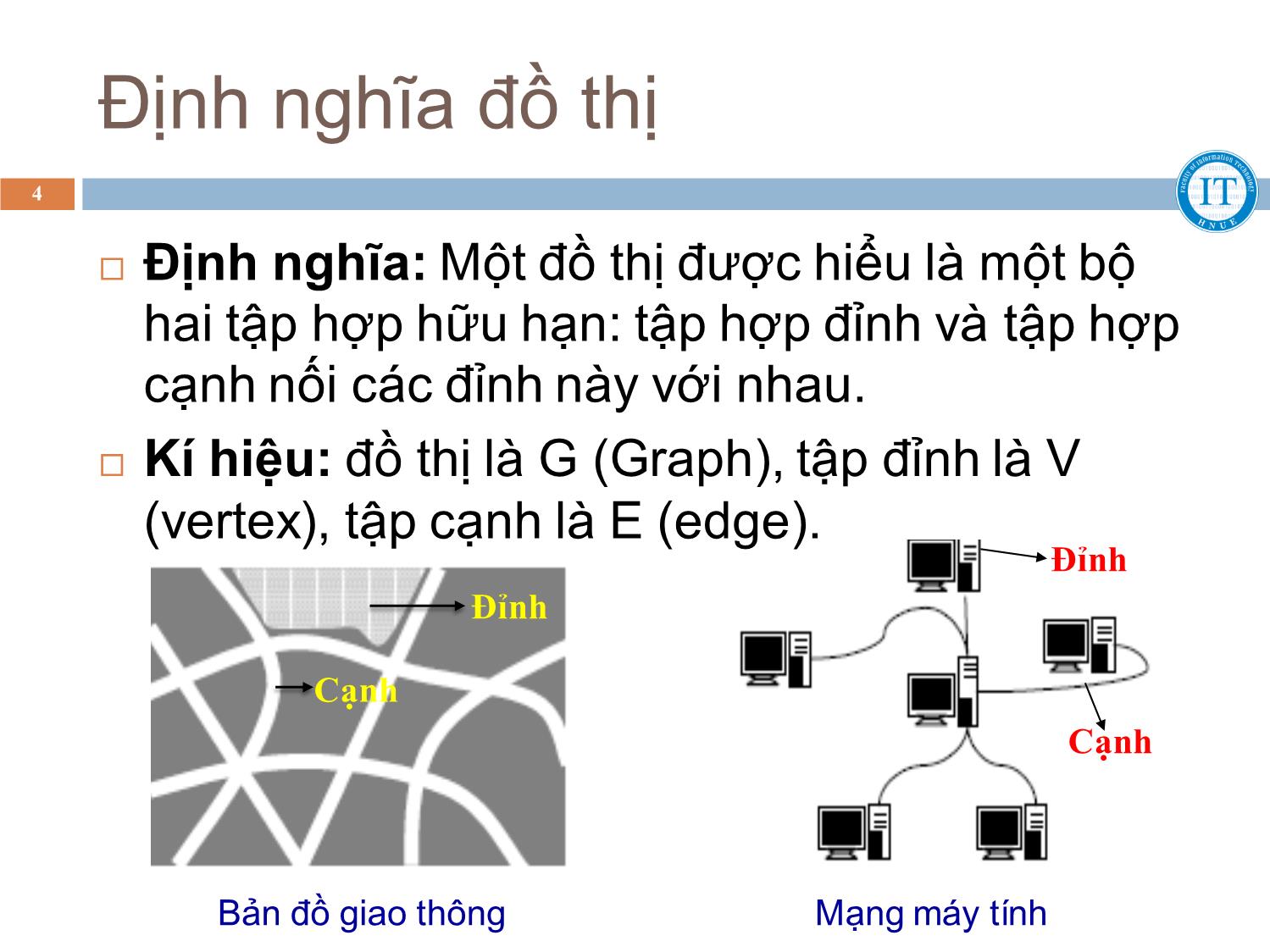
Bản đồ giao thông Mạng máy tính
Định nghĩa: Một đồ thị được hiểu là một bộ
hai tập hợp hữu hạn: tập hợp đỉnh và tập hợp
cạnh nối các đỉnh này với nhau.
Kí hiệu: đồ thị là G (Graph), tập đỉnh là V
(vertex), tập cạnh là E (edge).

Trang 1

Trang 2

Trang 3
Trang 4
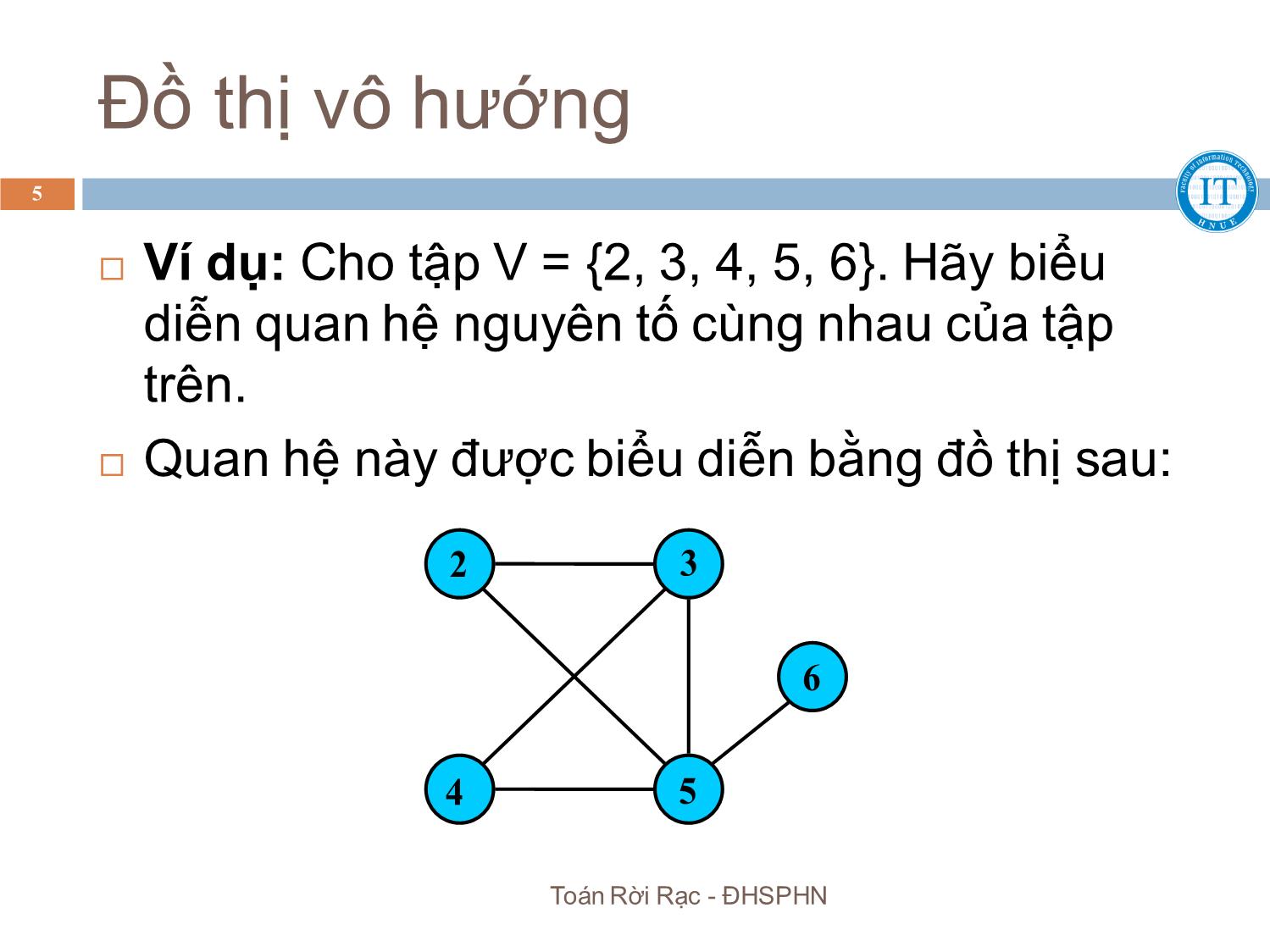
Trang 5

Trang 6
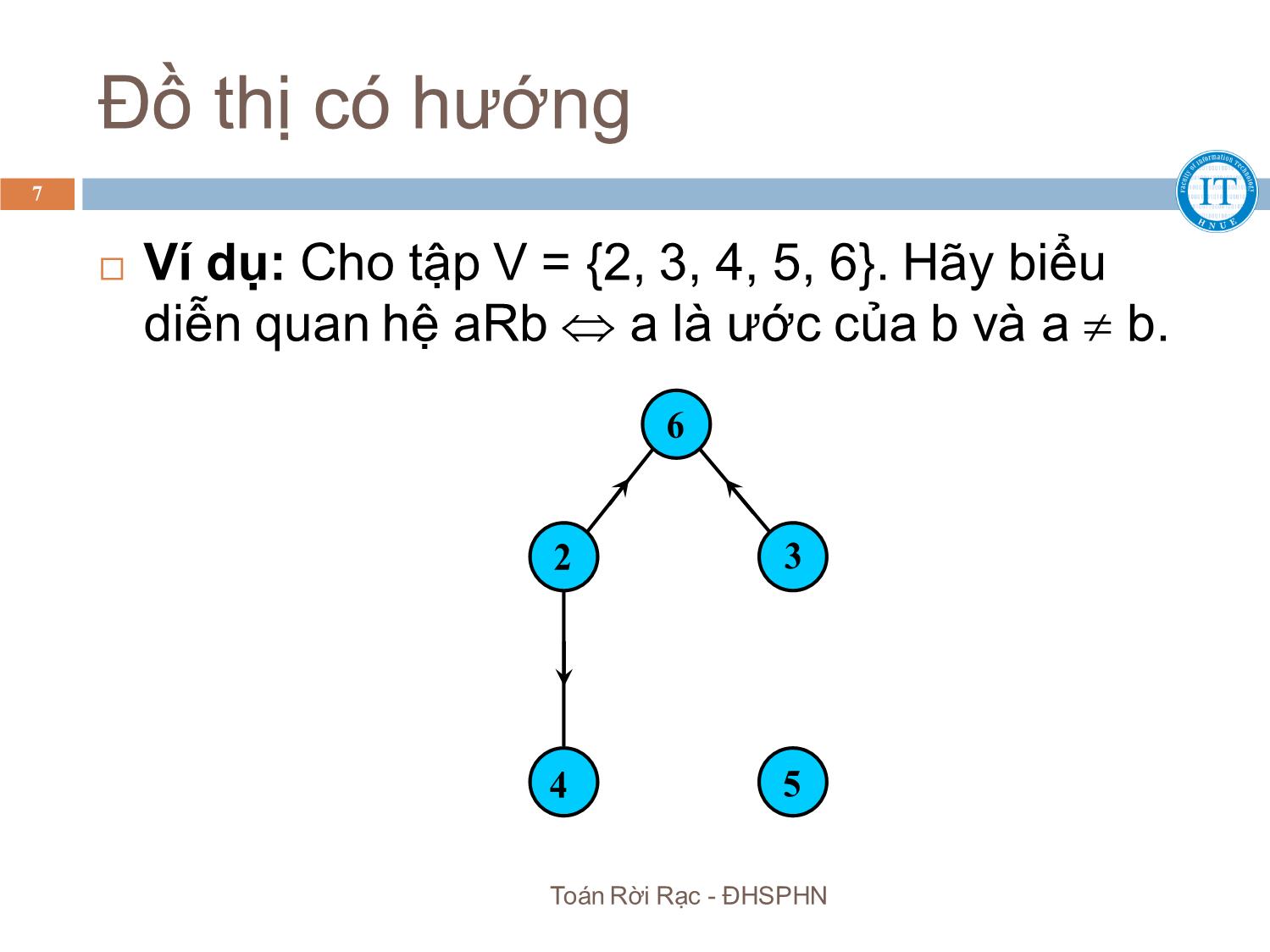
Trang 7

Trang 8

Trang 9

Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Toán rời rạc - Chương 7. Lý thuyết đồ thị - Bùi Thị Thủy", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Toán rời rạc - Chương 7. Lý thuyết đồ thị - Bùi Thị Thủy

u giữa hai đồ thị
70
Để chứng minh hàm f từ tập đỉnh của G lên
tập đỉnh của H là một phép đẳng cấu, ta phải
chỉ ra f bảo tồn các cạnh bằng cách sử dụng
ma trận liền kề.
f là đẳng cấu nếu như ma trận liền kề của G ≡
ma trận liền kề của H.
Toán Rời Rạc - ĐHSPHN
Sự đẳng cấu giữa hai đồ thị
71
Ví dụ: Hai đồ thị G và H như hình bên
G và H cùng có 6 đỉnh, 7 cạnh, 4 đỉnh bậc 2 và 2 đỉnh
bậc 3 thỏa mãn các bất biến là như nhau 1 2
Tìm phép đẳng cấu f: 5
Định nghĩa hàm f: 6
f : {1, 2, 3, 4, 5, 6} → {a, b, c, d, e, f}
4
f(1) = f f(2) = c f(3) = d G 3
f(4) = e f(5) = a f(6) = b a c
Chỉ ra f là một phép đẳng cấu: lập ma trận b
liền kề của G và H
f
e H d
Toán Rời Rạc - ĐHSPHN
Sự đẳng cấu giữa hai đồ thị
72
1 2 a c
b
5
6 f
4 G 3 e H d
1 2 3 4 5 6 f c d e a b
1 0 1 0 1 0 0 f 0 1 0 1 0 0
2 1 0 1 0 0 1 c 1 0 1 0 0 1
3 0 1 0 1 0 0 d 0 1 0 1 0 0
A = AH =
G 4 1 0 1 0 1 0 e 1 0 1 0 1 0
5 0 0 0 1 0 1 a 0 0 0 1 0 1
6 0 1 0 0 1 0 b 0 1 0 0 1 0
AG = AH. Vậy là phép đẳng cấu hay G và H là đẳng cấu.
Luyện tập
73
1. Biểu diễn đồ thị sau bằng ma trận liền kề và
ma trận liên thuộc.
c
2 4
a f
1 e g 6
d h
b 3 5
Toán Rời Rạc - ĐHSPHN
Luyện tập
74
2. Biểu diễn đồ thị sau bằng ma trận trọng số:
G 2 E B
2 2 2
3 2 1 D A
4 1 3
H F C
1
Toán Rời Rạc - ĐHSPHN
Luyện tập
75
3. Hãy xác định xem hai đồ thị sau có đẳng cấu
hay không?
v v
u1 1 2
u8 u 2
v5
v6
u7 u3
v7
v8
u6 u 4
u5 v4 v3
Toán Rời Rạc - ĐHSPHN
76 Đường một nét Euler
Toán Rời Rạc - ĐHSPHN
Đường một nét Euler
77
C
Kneiphof island
A D
B
C
A D
Bài toán 7 cây cầu thành Konigsberg
Toán Rời Rạc - ĐHSPHN B
Đường một nét Euler
78
Khái niệm: Cho một đồ thị vô hướng G = (V,
E) có n đỉnh, m cạnh. Đường một nét Euler
trong G là một dãy chứa tất cả m cạnh của đồ
thị và có dạng P1, e1, P2, e2, , Pm, em, Pm+1
sao cho cạnh ei là cạnh nối hai đỉnh Pi và Pi+1.
Nếu P1 = Pm+1 ta gọi đó là đường một nét
Euler khép kín
Nếu P1 ≠ Pm+1 ta gọi đó là đường một nét
Euler mở
Toán Rời Rạc - ĐHSPHN
Đường một nét Euler
79
Định lý 1: Đồ thị vô hướng và liên thông G =
(V, E) có đường một nét Euler khép kín bậc
của tất cả các đỉnh trong G là số chẵn.
Định lý 2: Điều kiện cần và đủ để một đồ thị
liên thông G có đường một nét Euler mở là số
đỉnh bậc lẻ trong đồ thị là 2.
Đồ thị Euler được ứng dụng trong các bài toán
thực tế như tìm hành trình ngắn nhất cho
người đưa thư, xe thu rác, cảnh sát tuần tra.
Toán Rời Rạc - ĐHSPHN
Đường một nét Euler
80
Ví dụ:
a 1 b
6
2
e G1
5 3
d 4 c
Đồ thị G1 có đường một nét Euler khép kín:
a, b, e, d, c, e, a.
Toán Rời Rạc - ĐHSPHN
Đường một nét Euler
81
Ví dụ:
a 1 b
2
6 5 4
7 3
e
d c
G2
Đồ thị G2 có đường một nét Euler mở:
a, d, c, e, b, c, a, b
Toán Rời Rạc - ĐHSPHN
Đường một nét Euler
82
Ví dụ: a b
e
G3
d c
Đồ thị G3 không có đường một nét Euler
Toán Rời Rạc - ĐHSPHN
Đường một nét Euler
83
Thuật toán tìm đường một nét Euler khép kín:
B1: Chọn đỉnh a làm đỉnh bắt đầu. Xây dựng
đường một nét khép kín con C’.
B2: Loại bỏ các cạnh trong C’ khỏi đồ thị. Loại bỏ
các đỉnh cô lập (nếu có).
B3: Lấy một đỉnh chung của C’ và đồ thị còn lại
để xây dựng đường một nét con tiếp theo C’’. Rồi
ghép vào C’ và quay lại bước 2. Lặp cho đến khi
các cạnh được đưa hết vào C’.
Toán Rời Rạc - ĐHSPHN
Đường một nét Euler
84
Ví dụ:
A B
C D
E F
G G’ G’’
- Chọn A là đỉnh bắt đầu.
- B1: C’ = A, C, E, A
- B2: Thu được đồ thị G’
- B3: Chọn đỉnh A tiếp, C’’ = A, D, B, A C’ = A, C, E, A, D, B, A
- B2: Thu được G’’
- B3: Chọn đỉnh D, C’’ = D, E, F, D C’ = A, C, E, A, D, E, F, D, B, A
Luyện tập
85
Toán Rời Rạc - ĐHSPHN
86 Chu trình Hamilton
Toán Rời Rạc - ĐHSPHN
Chu trình Hamilton
87
Khái niệm: Cho đồ thị G = (V, E). Một chu
trình C được gọi là chu trình Hamilton nếu nó
đi qua tất cả các đỉnh của đồ thị.
Nếu tồn tại đường đi H có tính chất như trên
thì H được gọi là đường đi Hamilton.
Vấn đề tìm chu trình Hamilton trong đồ thị
được nhà toán học Anh là Hamilton nêu ra
năm 1858.
Toán Rời Rạc - ĐHSPHN
Chu trình Hamilton
88
Ví dụ:
a b a b a b
d c d c d c
G1 G2 G3
• G1 không chứa đường đi và chu trình Hamilton
• G2 chứa đường đi Hamilton
• G3 chứa chu trình Hamilton
Toán Rời Rạc - ĐHSPHN
Thuật toán liệt kê chu trình Hamilton
89
Procedure Hamilton(k);
Begin
For y ∈ Ke(X[k-1]) do
If (k =N+1) and (y=v0) then Ghinhan(X[1],. . . , X[n], v0)
Else if Chuaxet[y] then
Begin
X[k] := y;
Chuaxet[y] := False;
Hamilton(k+1);
Chuaxet[y] := True;
End;
End;
Toán Rời Rạc - ĐHSPHN
Thuật toán liệt kê chu trình Hamilton
90
Ví dụ:
A
B D E
CC
Toán Rời Rạc - ĐHSPHN
Luyện tập
91
Toán Rời Rạc - ĐHSPHN
92 Bài toán tìm đường đi ngắn nhất
Toán Rời Rạc - ĐHSPHN
Bài toán thực tế
93
Có 6 điểm du lịch trong một khu sinh thái là a, b,
c, d, e, z. Giữa hai điểm có thể có hoặc không có
đường đi trực tiếp.
Hãy tìm đường đi có khoảng cách ngắn nhất từ điểm
a đến z.
Bài toán được mô hình hoá bằng đồ thị có trọng
số như sau:
Mỗi đỉnh biểu diễn một điểm du lịch.
Hai đỉnh có cạnh nối nếu có đường đi trực tiếp.
Trọng số của cạnh được gán là khoảng cách từ điểm
này sang điểm kia.
Toán Rời Rạc - ĐHSPHN
Bài toán thực tế
94
Đồ thị mô hình bài toán:
5
b c
2 2
a 2 z
3 4
d e
1
Đường đi ngắn nhất là đường đi có tổng trọng
số các cạnh của nó là nhỏ nhất
Toán Rời Rạc - ĐHSPHN
Thuật toán Dijkstra
95
Bài toán: Tìm đường đi ngắn nhất từ đỉnh a
đến z của đồ thị có trọng số liên thông G=(V,E)
Năm 1959, nhà toán học người Hà Lan
E.Dijkstra đề xuất thuật toán Dijkstra để giải
quyết bài toán trên.
Gọi L(v) là độ dài đường đi ngắn nhất từ đỉnh a
đến đỉnh v.
S là tập các đỉnh đã tìm được đường đi ngắn
nhất từ a đến nó.
Toán Rời Rạc - ĐHSPHN
Thuật toán Dijkstra
96
Thuật toán Dijkstra:
Bước 1: L(a) = 0, S = Ø, v V, v a: L(v) =
Bước 2: Nếu z S thì kết thúc.
Bước 3: Chọn v S sao cho L(v) là nhỏ nhất.
Đưa v vào S.
Bước 4: Với mỗi đỉnh x liền kề v và x S thì đặt:
L(x) = min{L(x), L(v) + c(v,x)}
Quay lại bước 2.
Toán Rời Rạc - ĐHSPHN
Ví dụ
97
e
Ví dụ 1: 5
b c
2 2
a 2 z
a c
3 4
d e
1
b
B1: L(a) = 0; S = , L(b) = L(c) = L(d) = L(e) = L(z) =
B3: v = a, S = {a}
B4: L(b) = min{, 2 + 0} = 2, L(d) = min{, 3 + 0} = 3
B3: v = b, S = {a,b}
B4: L(c) = 7, L(e) = 4, L(d) = 3, L(z)=
B3: v = e, S = {a,b,d,e}
Ví dụ
98
e
Ví dụ 1: 5
b c
2 2
a 2 z
a c
3 4
d e
1
b
B4: L(c) = 5, L(z) = 8
B3: v = c, S = {a, b, d, e, c}
B4: L(z) = 7
B3: v = z, S = {a, b, d, e, c, z}
Về bước 2: kết thúc
Ví dụ
99
Ví dụ 2:
5
B C
2 2
2
A 1
Z
3
1 4
D E
Toán Rời Rạc - ĐHSPHN
Ví dụ
100
Ví dụ 2:
L(B) = 2
5
B C
2 2
2
A 1
Z
3
L(A) = 0
1 4
D E
L(D) = 3
Toán Rời Rạc - ĐHSPHN
Ví dụ
101
Ví dụ 2:
L(B) = 2 L(C) = 7
5
B C
2 2
2
A 1
Z
3
L(A) = 0
1 4
D E
L(D) = 3 L(E) = 4
Toán Rời Rạc - ĐHSPHN
Ví dụ
102
Ví dụ 2:
L(B) = 2 L(C) = 7
5
B C
2 2
2
A 1
Z
3
L(A) = 0
1 4
D E
L(D) = 3 L(E) = 4
Toán Rời Rạc - ĐHSPHN
Ví dụ
103
Ví dụ 2:
L(B) = 2 L(C) = 5
5
B C
2 2
2
A 1
Z
3
L(A) = 0
1 4 L(Z) = 8
D E
L(D) = 3 L(E) = 4
Toán Rời Rạc - ĐHSPHN
Ví dụ
104
Ví dụ 2:
L(B) = 2 L(C) = 5
5
B C
2 2
2
A 1
Z
3
L(A) = 0
1 4 L(Z) = 7
D E
L(D) = 3 L(E) = 4
Toán Rời Rạc - ĐHSPHN
Ví dụ
105
L(B) = 2 L(C) = 5
Ví dụ 2: 5
B C
2 2
2
A 1
Z
3
L(A) = 0
1 4 L(Z) = 7
D E
L(D) = 3 L(E) = 4
Đường đi ngắn nhất từ A đến Z được tô màu đỏ, qua các đỉnh:
A – B – E – C – Z, Tổng trọng số 7
Toán Rời Rạc - ĐHSPHN
Ví dụ
106
Netwark
Ví dụ 3: Netwark → CapeMay
20
Trenton
42 Wood Brige
35
30 40
60 Asbury Park
75
55
Atlantic City
Camden
85 45
CapeMay
Toán Rời Rạc - ĐHSPHN
Ví dụ
107 Netwark
Ví dụ 3: 0
20
Trenton
42 20 Wood Brige (Net)
35
30 40
60 Asbury Park
75
55
Atlantic City
Camden
85 45
CapeMay
Toán Rời Rạc - ĐHSPHN
Ví dụ
108 Netwark
Ví dụ 3: 0
20
Trenton (Wood)
42 20
62 Wood Brige (Net)
35
30 40
60 55 Asbury Park (Wood)
75
55
80 Atlantic City
Camden (Wood)
85 45
CapeMay
Toán Rời Rạc - ĐHSPHN
Ví dụ
109 Netwark
Ví dụ 3: 0
20
Trenton (Wood)
42 20
62 Wood Brige (Net)
35
30 40
60 55 Asbury Park (Wood)
75
55
80 130 Atlantic City (Asbury)
Camden (Wood)
85 45
CapeMay
Toán Rời Rạc - ĐHSPHN
Ví dụ
110 Netwark
Ví dụ 3: 0
20
Trenton (Wood)
42 20
62 Wood Brige (Net)
35
30 40
60 55 Asbury Park (Wood)
75
55
80 130 Atlantic City (Asbury)
Camden (Wood)
85 45
CapeMay
Toán Rời Rạc - ĐHSPHN
Ví dụ
111 Netwark
Ví dụ 3: 0
20
Trenton (Wood)
42 20
62 Wood Brige (Net)
35
30 40
60 55 Asbury Park (Wood)
75
55
80 130 Atlantic City (Asbury)
Camden (Wood)
85 45
165 CapeMay (Cam)
Toán Rời Rạc - ĐHSPHN
Ví dụ
112 Netwark
Ví dụ 3: 0
20
Trenton (Wood)
42 20
62 Wood Brige (Net)
35
30 40
60 55 Asbury Park (Wood)
75
55
80 130 Atlantic City (Asbury)
Camden (Wood)
85 45
165 CapeMay (Cam)
Toán Rời Rạc - ĐHSPHN
Ví dụ
113 Netwark
Ví dụ 3: 0
20
Trenton (Wood)
42 20
62 Wood Brige (Net)
35
30 40
60 55 Asbury Park (Wood)
75
55
80 130 Atlantic City (Asbury)
Camden (Wood)
85 45
165 CapeMay (Cam)
Toán Rời Rạc - ĐHSPHN
Ví dụ
114
Netwark
Ví dụ 3 0
20
Trenton (Wood)
42 20
62 Wood Brige (Net)
35
30 40
60 55 Asbury Park (Wood)
75
80 55
130 Atlantic City (Asbury)
Camden (Wood)
85 45
165 CapeMay (Cam)
Vậy đường đi ngắn nhất từ Netwark đến CapeMay có độ dài 165:
Netwark → Wood Brige → Camden → CapeMay
Toán Rời Rạc - ĐHSPHN
Luyện tập
115
1. Tìm đường đi ngắn nhất trên đồ thị cho bởi
hình bên:
a. Từ đỉnh A đến đỉnh H.
b. Từ đỉnh B đến đỉnh F.
Toán Rời Rạc - ĐHSPHN
Luyện tập
116
2. Tự vẽ một đồ thị đơn, vô hướng, các đỉnh liên
thông với nhau gồm 8 đỉnh và 14 cạnh. Tìm
đường đi ngắn nhất từ hai đỉnh tùy ý:
a. Trọng số của mỗi cạnh là 1.
b. Tự đánh trọng số cho các cạnh.
Toán Rời Rạc - ĐHSPHN
117 Cây khung của đồ thị
Toán Rời Rạc - ĐHSPHN
Định nghĩa cây khung
118
Định nghĩa: Cho đồ thị G = (V, E) là một đồ thị vô
hướng liên thông. Một đồ thị con G’ của G được
gọi là cây khung (hay cây bao trùm) của G nếu:
G’ là một cây
G’ chứa tất cả các đỉnh của cây
Ví dụ:
b
b b b
c
c c
a a a c
a
d
d d
e e e e d
G
G G1 G2 3
Xác định cây khung
119
Xác định cây khung là việc xây dựng một cây
chứa tất cả các đỉnh của đồ thị.
Hai thuật toán xác định cây khung là:
Xác định ưu tiên theo chiều rộng
Xác định ưu tiên theo chiều sâu
Toán Rời Rạc - ĐHSPHN
Theo chiều rộng (BFS)
120
Bước 1: Lấy một đỉnh a làm gốc của cây khung.
Bước 2: Ghép các cạnh liên thuộc với gốc. Các đỉnh kề
với gốc trong bước này có mức là 1.
Bước 3: Tiếp tục ghép các cạnh liên thuộc đỉnh mức 1
sao cho không tạo chu trình. Các đỉnh được đưa vào ở
bước này có mức là 2.
Bước 4: Tiếp tục quá trình khi tất cả các đỉnh đã được
ghép vào cây.
Toán Rời Rạc - ĐHSPHN
Theo chiều rộng (BFS)
121
Đỉnh Tập đỉnh chờ Cây khung
B F G
A B(A),C(A), D(A) A
B C(A), D(A), F(B) A, B A D
C D(A), F(B) A, B, C
C E
D F(B), E(D), G(D) A, B, C, D
F E(D), G(D) A, B, C, D, F Cây khung tìm được có
cạnh tô màu đỏ
E G(D) A, B, C, D, F, E
G A, B, C, D, F, E, G
Toán Rời Rạc - ĐHSPHN
Theo chiều sâu (DFS)
122
Bước 1: Lấy một đỉnh a làm gốc của cây khung.
Bước 2: Xây dựng đường đi từ đỉnh này bằng cách
ghép lần lượt các cạnh vào. Mỗi cạnh được ghép vào
nối đỉnh cuối cùng của đường đi và một đỉnh chưa thuộc
đường đi. Thực hiện đến khi không ghép được thêm
cạnh nào nữa.
Bước 3: Nếu đường đi chứa tất cả các đỉnh của đồ thị
thì đó chính là cây khung. Nếu không thì chuyển sang
bước 4.
Bước 4: Quay lui lại đỉnh ngay trước đỉnh cuối cùng của
đường đi và xây dựng đường đi mới bắt đầu từ đỉnh
này. Nếu không được thì lùi tiếp đỉnh nữa.
Toán Rời Rạc - ĐHSPHN
Theo chiều sâu (DFS)
123
Ví dụ:
B F G
A D
C E
Toán Rời Rạc - ĐHSPHN
124 Cây khung nhỏ nhất
Toán Rời Rạc - ĐHSPHN
Cây khung nhỏ nhất
125
Định nghĩa: Cây khung nhỏ nhất trong một
đồ thị liên thông, có trọng số là một cây khung
có tổng trọng số trên các cạnh của nó là nhỏ
nhất.
Thuật toán tìm cây khung nhỏ nhất:
Prim (Robert Prim - 1957)
Kruskal (Joseph Kruskal – 1965)
Toán Rời Rạc - ĐHSPHN
Thuật toán Prim
126
Đồ thị G = (V, E) liên thông, có n đỉnh.
Bước 1: Chọn một cạnh bất kỳ có trọng số nhỏ nhất,
đặt nó vào cây khung.
Bước 2: Lần lượt ghép vào cây các cạnh có trọng số
nhỏ nhất liên thuộc với một đỉnh của cây và không tạo
ra chu trình trong cây.
Bước 3: Thuật toán dừng lại khi (n 1) cạnh được
ghép vào cây.
Toán Rời Rạc - ĐHSPHN
Thuật toán Prim
127
Ví dụ: Bằng thuật toán Prim
A 4 B
3 5
6 C 1
E D
3
2 6
G F
Cạnh đã được chọn Cây khung nhỏ nhất của G
Cạnh đang xét chọn Tổng trọng số là 12
Toán Rời Rạc - ĐHSPHN
Thuật toán Kruskal
128
Đồ thị G = (V, E) liên thông, có n đỉnh.
Bước 1: Chọn một cạnh bất kỳ có trọng số nhỏ nhất,
đặt nó vào cây khung.
Bước 2: Lần lượt ghép vào cây các cạnh có trọng số
nhỏ nhất mà không tạo ra chu trình trong cây.
Bước 3: Thuật toán dừng lại khi (n 1) cạnh được
ghép vào cây.
Toán Rời Rạc - ĐHSPHN
Thuật toán Kruskal
129
Ví dụ: Bằng thuật toán Kruskal
A 4 B
3 5
6 C 1
E D
3
2 6
G F
Cây khung của G
Cạnh đã được chọn
Tổng trọng số 12
Toán Rời Rạc - ĐHSPHN
Luyện tập
130
1. Hãy mô tả các bước xét các đỉnh trong quá
trình tìm đường đi từ đỉnh s tới đỉnh z trong đồ
thị bên
a. Theo chiều rộng
b. Theo chiều sâu.
Toán Rời Rạc - ĐHSPHN
Luyện tập
131
2. Hãy tìm cây khung nhỏ nhất của đồ thị G có
trọng số trong hình bên bằng thuật toán Prim
và thuật toán Kruskal?
Toán Rời Rạc - ĐHSPHN
THANK YOU!
File đính kèm:
 bai_giang_toan_roi_rac_chuong_7_ly_thuyet_do_thi_bui_thi_thu.pdf
bai_giang_toan_roi_rac_chuong_7_ly_thuyet_do_thi_bui_thi_thu.pdf

