Bài giảng Toán rời rạc - Chương 5: Đồ thị - Nguyễn Quỳnh Diệp
NỘI DUNG
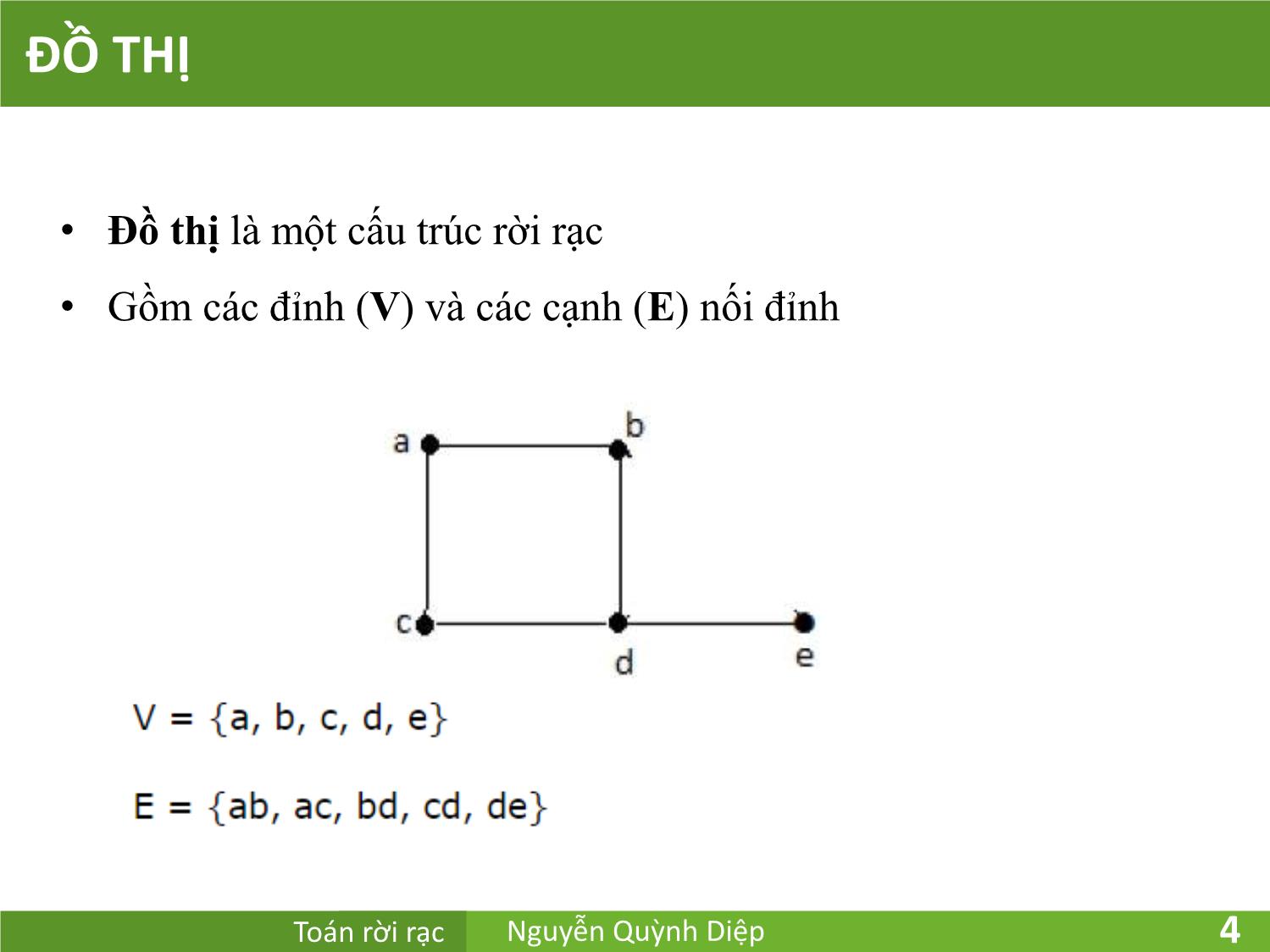
• Các định nghĩa
• Các thuật ngữ về đồ thị
• Biểu diễn đồ thị
• Tính liên thông
• Đường đi Euler và đường đi Hamilton
• Bài toán đường đi ngắn nhất

Trang 1

Trang 2

Trang 3
Trang 4

Trang 5

Trang 6

Trang 7
Trang 8
Trang 9
Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Toán rời rạc - Chương 5: Đồ thị - Nguyễn Quỳnh Diệp", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Toán rời rạc - Chương 5: Đồ thị - Nguyễn Quỳnh Diệp

ỉnh là số các cạnh liên
thuộc với nó, riêng khuyên tại một đỉnh được tính hai lần cho
bậc của nó. Kí hiệu bậc của đỉnh v là deg(v)
Toán rời rạc Nguyễn Quỳnh Diệp 19
ĐỒ THỊ VÔ HƯỚNG
Ví dụ 1: Bậc của các đỉnh trong các đồ thị sau là bao nhiêu?
• Đỉnh bậc 0 gọi là đỉnh cô lập (ví dụ đỉnh g trong G)
• Đỉnh bậc 1 gọi là đỉnh treo (ví dụ đỉnh d trong G, c trong H)
Toán rời rạc Nguyễn Quỳnh Diệp 20
ĐỒ THỊ VÔ HƯỚNG
Định lí 1:
ĐỊNH LÍ BẮT TAY. Cho G = (V, E) là một đồ thị vô hướng.
Khi đó:
|푬| = 풅풆품(풗)
풗∈푽
(Định lý đúng với cả khi đồ thị vô hướng có cạnh bội hoặc khuyên)
Định lí 2:
Một đồ thị vô hướng có một số chẵn các đỉnh bậc lẻ
Toán rời rạc Nguyễn Quỳnh Diệp 21
ĐỒ THỊ CÓ HƯỚNG
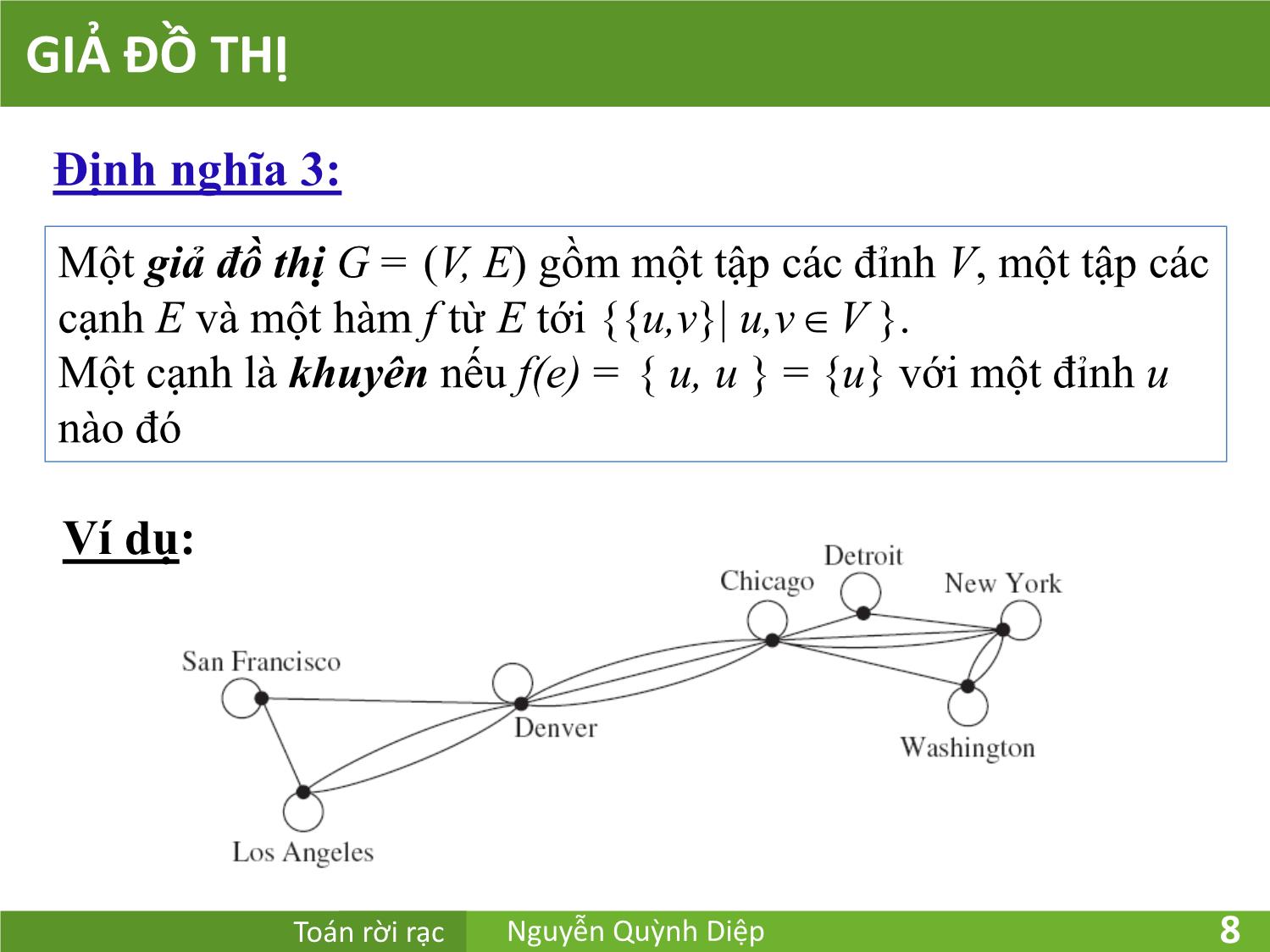
Định nghĩa 3:
Trong đồ thị có hướng G, nếu (u, v) là cạnh của G thì u được
gọi là nối tới v và v được gọi là được nối từ u.
Đỉnh u gọi là đỉnh đầu, đỉnh v gọi là đỉnh cuối của cạnh (u,v).
Đỉnh đầu và đỉnh cuối của khuyên trùng nhau.
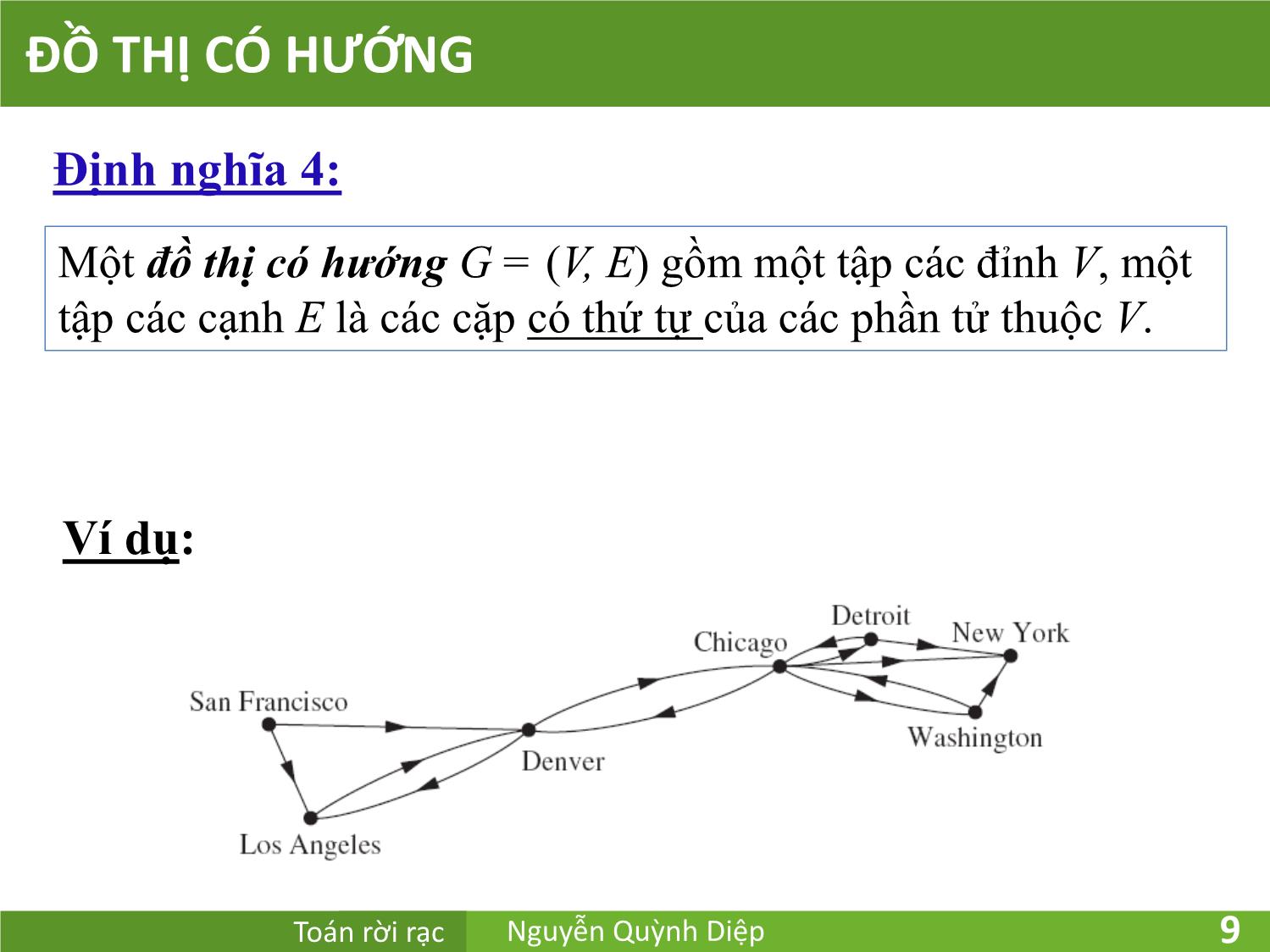
Định nghĩa 4:
Trong đồ thị có hướng bậc-vào của đỉnh v kí hiệu deg (v) là số
các cạnh có đỉnh cuối là v. Bậc-ra của đỉnh v, kí hiệu deg+(v) là
số các cạnh có đỉnh đầu là v.
Toán rời rạc Nguyễn Quỳnh Diệp 22
ĐỒ THỊ CÓ HƯỚNG
Ví dụ 2: Tìm bậc-vào và bậc-ra của mỗi định trong đồ thị sau:
Định lí 3:
Gọi G = (V,E) là một đồ thị có hướng. Khi đó:
풅풆품− 풗 = 풅풆품+ 풗 = |푬|
풗∈푽 풗 ∈푽
Toán rời rạc Nguyễn Quỳnh Diệp 23
MỘT SỐ ĐỒ THỊ ĐẶC BIỆT
Đồ thị đầy đủ n đỉnh:
Kí hiệu Kn
Là đơn đồ thị
Giữa mỗi cặp đỉnh phân biệt chỉ có 1 cạnh nối chúng
Toán rời rạc Nguyễn Quỳnh Diệp 24
MỘT SỐ ĐỒ THỊ ĐẶC BIỆT
Đồ thị vòng n đỉnh:
Kí hiệu Cn , n 3
Có n đỉnh v1, v2, ..., vn
Các cạnh {v1, v2}, {v2, v3},..., {vn-1, vn} và {vn, v1}
Toán rời rạc Nguyễn Quỳnh Diệp 25
MỘT SỐ ĐỒ THỊ ĐẶC BIỆT
Đồ thị hình bánh xe:
Kí hiệu Wn , n 3
Là đồ thị vòng Cn bổ sung thêm 1 đỉnh mà đỉnh này nối
với mọi đỉnh đã có trong Cn tạo thành các cạnh mới
Toán rời rạc Nguyễn Quỳnh Diệp 26
MỘT SỐ ĐỒ THỊ ĐẶC BIỆT
Các khối n chiều:
Ký hiệu Qn
Là đồ thị có 2n đỉnh, mỗi đỉnh là 1 xâu nhị phân độ dài n
Hai đỉnh liền kề nếu các xâu nhị phân biểu diễn chúng chỉ
khác nhau đúng1 bit
Toán rời rạc Nguyễn Quỳnh Diệp 27
ĐỒ THỊ PHÂN ĐÔI
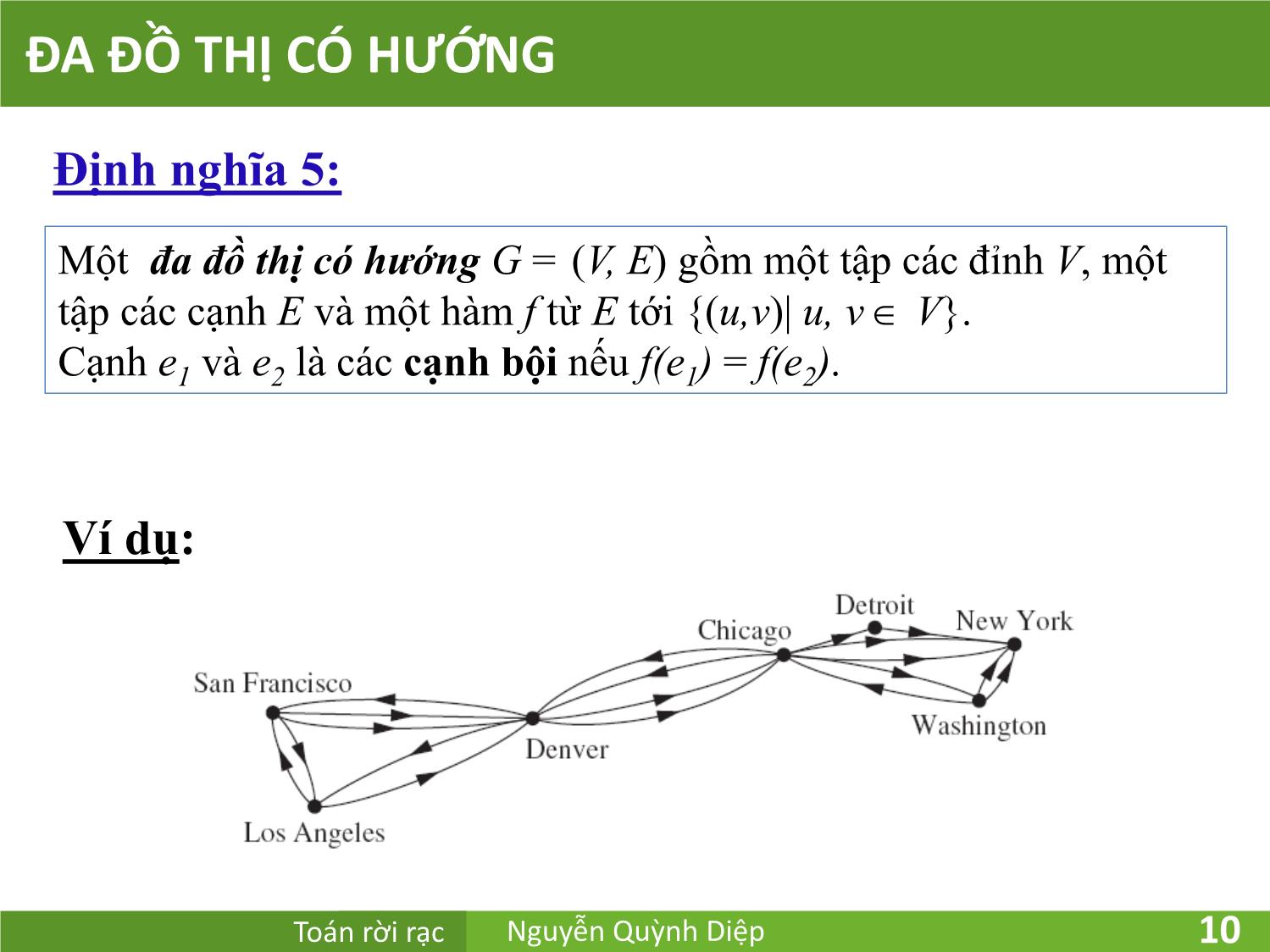
Định nghĩa 5:
G là đồ thị phân đôi nếu G là đơn đồ thị và tập V các đỉnh có thể
phân thành 2 tập con khác rỗng, rời nhau V1 và V2 sao cho mỗi cạnh
của đồ thị nối một đỉnh của V1 với một đỉnh của V2.
Chú ý: G là đồ thị phân đôi thì không nhất thiết mỗi đỉnh của V1
phải nối với tất cả các đỉnh của V2
Toán rời rạc Nguyễn Quỳnh Diệp 28
BÀI TẬP
. Bài 3: Các đồ thị đã cho có là
phân đôi không?
29
Toán rời rạc Nguyễn Quỳnh Diệp 29
ĐỒ THỊ CON
Định nghĩa 6:
Đồ thị con của đồ thị G = (V, E) là đồ thị H = (W, F), trong đó
W V và F E
Toán rời rạc Nguyễn Quỳnh Diệp 30
HỢP CỦA HAI ĐỒ THỊ
Định nghĩa 7:
Hợp của hai đơn đồ thị G1 = (V1, E1) và G2 = (V2, E2) là một đơn
đồ thị có tập các đỉnh là V1 V2 và tập các cạnh E1 E2. Ta kí
hiệu hợp của các đồ thị G1 và G2 là G1 G2.
Toán rời rạc Nguyễn Quỳnh Diệp 31
BÀI TẬP
. Bài 4: Tìm hợp của cặp hai đơn đồ thị sau
32
Toán rời rạc Nguyễn Quỳnh Diệp 32
5.3. BIỂU DIỄN ĐỒ THỊ
Toán rời rạc Nguyễn Quỳnh Diệp 33
BIỂU DIỄN ĐỒ THỊ
Biểu diễn đồ thị
• Danh sách kề
• Ma trận kề
• Ma trận liên thuộc
Toán rời rạc Nguyễn Quỳnh Diệp 34
DANH SÁCH KỀ
Chỉ rõ các đỉnh nối với mỗi đỉnh của đồ thị không có
Danh sách kề của
cạnh bội đơn đồ thị
Đỉnh Các đỉnh kề
Danh sách kề của
đồ thị có hướng
Đỉnh đầu Đỉnh cuối
Toán rời rạc Nguyễn Quỳnh Diệp 35
MA TRẬN KỀ
• Giả sử G = (V, E) là một đơn đồ thị, trong đó |V| = n
• Ma trận kề A = [aij], là ma trận n n trong đó:
풏ế풖 풗풊, 풗풋 풍à ộ풕 ạ풏풉 ủ 푮
풊풋 =
풏ế풖 풌풉ô풏품 ó ạ풏풉 풏ố풊 đỉ풏풉 풗풊 풗ớ풊 đỉ풏풉 풗풋
v1 v2 v3 v4
v1
v2 a23 = 1
v3
v4
Toán rời rạc Nguyễn Quỳnh Diệp 36
MA TRẬN KỀ
• Có n! ma trận kề khác nhau của một đồ thị n đỉnh
• Trường hợp đa đồ thị, giả đồ thị thì phần tử vị trí (i,j) bằng số
cạnh nối các đỉnh ai và aj
• Trường hợp đồ thị có hướng: aij = {vi,vj}, vi : đỉnh đầu, vj: đỉnh
cuối Đỉnh cuối
v1 v2 v3 v4
v1
Đỉnh đầu v2
v
3 a23 = 1
v4
Toán rời rạc Nguyễn Quỳnh Diệp 37
MA TRẬN KỀ
Ví dụ 1: a b c d
a
b
c
d
Ví dụ 2:
a b c d
a
b
c
d
Toán rời rạc Nguyễn Quỳnh Diệp 38
MA TRẬN LIÊN THUỘC
• Giả sử G = (V, E) là một đơn đồ thị vô hướng
• Có tập đỉnh v1, v2,...,vn và tập cạnh e1, e2, ..., em
• Ma trận liên thuộc gồm m cột, n hàng, M = [mij] trong đó:
풏ế풖 풆풋 풏ố풊 풗ớ풊 đỉ풏풉 풗풊
풊풋 =
풏ế풖 풆풋 풌풉ô풏품 풏ố풊 풗ớ풊 đỉ풏풉 풗풊
m23 = 1
• Ma trận liên thuộc có thể biểu diễn các cạnh bội và khuyên
Toán rời rạc Nguyễn Quỳnh Diệp 39
MA TRẬN LIÊN THUỘC
Ví dụ 3:
Toán rời rạc Nguyễn Quỳnh Diệp 40
BÀI TẬP
. Bài 5: Biểu diễn đồ thị sau bằng ma trận kề
. Bài 6: Biểu diễn đồ thị sau bằng ma trận liên thuộc
41
Toán rời rạc Nguyễn Quỳnh Diệp 41
5.4. TÍNH LIÊN THÔNG
Toán rời rạc Nguyễn Quỳnh Diệp 42
ĐƯỜNG ĐI
Định nghĩa 1:
• Đường đi độ dài n từ u tới v, n Z+ của đồ thị vô hướng là
dãy các cạnh e1, e2,..., en sao cho f(e1) = {x0, x1}, f(e2) = {x1,
x2},..., f(en) = {xn-1, xn} với x0 = u và xn = v
• Đường đi gọi là chu trình nếu điểm đầu và điểm cuối của
đường đi trùng nhau.
• Đường đi gọi là đường đi đơn nếu nó không đi qua một
cạnh quá 1 lần
• Chu trình gọi là chu trình đơn nếu nó không đi qua một
cạnh quá 1 lần
Toán rời rạc Nguyễn Quỳnh Diệp 43
ĐƯỜNG ĐI
Ví dụ 1:
• Chỉ ra một đường đi đơn độ dài 4?
• Chỉ ra một đường chu trình độ dài 4?
• Chỉ ra đường đi độ dài 5 không là đường đi đơn?
Toán rời rạc Nguyễn Quỳnh Diệp 44
TÍNH LIÊN THÔNG – ĐỒ THỊ VÔ HƯỚNG
Định nghĩa 3:
• Một đồ thị vô hướng được gọi là liên thông nếu có đường
đi giữa mọi cặp đỉnh phân biệt của đồ thị
G1 G2
Toán rời rạc Nguyễn Quỳnh Diệp 45
TÍNH LIÊN THÔNG – ĐỒ THỊ VÔ HƯỚNG
Định lí 1:
Giữa mọi cặp đỉnh phân biệt của một đồ thị vô hướng liên
thông luôn có đường đi đơn
• Đồ thị KHÔNG liên thông sẽ là hợp của hai hay nhiều đồ thị con
liên thông
• Các đồ thị con liên thông rời nhau gọi là các thành phần liên
thông
• Đỉnh cắt: là đỉnh khi xóa đi tạo ra đồ thị con mới có nhiều thành
phần liên thông hơn đồ thị ban đầu. Xóa đỉnh cắt sẽ tạo ra đồ thị
con KHÔNG liên thông
• Cạnh cắt (cầu): là cạnh nếu bỏ đi sẽ tạo ra một đồ thị có nhiều
thành phần liên thông hơn đồ thị ban đầu
Toán rời rạc Nguyễn Quỳnh Diệp 46
TÍNH LIÊN THÔNG – ĐỒ THỊ VÔ HƯỚNG
Ví dụ 2: Tìm đỉnh cắt và cạnh cắt của đồ thị sau?
Toán rời rạc Nguyễn Quỳnh Diệp 47
TÍNH LIÊN THÔNG – ĐỒ THỊ CÓ HƯỚNG
Định nghĩa 4:
Đồ thị có hướng gọi là liên thông mạnh nếu có đường đi từ a tới b
VÀ từ b tới a với MỌI đỉnh a và b của đồ thị.
Định nghĩa 5:
Đồ thị có hướng gọi là liên thông yếu nếu có đường đi giữa hai
đỉnh bất kì của đồ thị vô hướng nền (có đường đi khi không quan
tâm đến hướng)
Toán rời rạc Nguyễn Quỳnh Diệp 48
BÀI TẬP
. Bài 7: Các đồ thị sau có liên thông không?
49
Toán rời rạc Nguyễn Quỳnh Diệp 49
BÀI TẬP
. Bài 8: Chỉ ra các đồ thị sau đây có là liên thông mạnh không?
có là liên thông yếu không? Tìm các thành phần liên thông
mạnh
50
Toán rời rạc Nguyễn Quỳnh Diệp 50
5.5. ĐƯỜNG ĐI EULER VÀ HAMILTON
Toán rời rạc Nguyễn Quỳnh Diệp 51
ĐƯỜNG ĐI VÀ CHU TRÌNH EULER
Bài toán Königsberg
• Thành phố Königsberg chia thành 4 vùng bởi các nhánh sông
Pregel.
• Người ta đã xây 7 cây cầu để nối 4 vùng
• Hỏi có thể xuất phát tại 1 điểm để đi qua tất cả các cầu, mỗi
chiếc cầu không đi qua nhiều hơn 1 lần rồi trở về điểm xuất
phát?
Toán rời rạc Nguyễn Quỳnh Diệp 52
ĐƯỜNG ĐI VÀ CHU TRÌNH EULER
• Nhắc lại:
• Đường đi là một dãy các cạnh e1, e2,, en
• Đường đi gọi là chu trình nếu điểm đầu và điểm cuối của đường đi trùng
nhau.
• Đường đi đơn là đường đi chỉ đi qua mỗi cạnh không quá 1 lần.
• Chu trình đơn là chu trình chỉ đi qua mỗi cạnh không quá 1 lần
Định nghĩa 1:
• Đường đi Euler trong G là đường đi đơn đi qua tất cả các cạnh
của G.
• Chu trình Euler là chu trình đơn đi qua tất cả các cạnh của đồ
thị G.
Toán rời rạc Nguyễn Quỳnh Diệp 53
ĐƯỜNG ĐI VÀ CHU TRÌNH EULER
Ví dụ 1: Đồ thị nào sau đây có chu trình Euler?
Toán rời rạc Nguyễn Quỳnh Diệp 54
ĐIỀU KIỆN CẦN VÀ ĐỦ CHO CHU TRÌNH EULER
Định lí 1:
Một đa đồ thị liên thông có chu trình Euler nếu và chỉ nếu
mỗi đỉnh của nó đều có bậc chẵn.
Toán rời rạc Nguyễn Quỳnh Diệp 55
CHU TRÌNH EULER
Bài toán Königsberg
• Thành phố Königsberg chia thành 4 vùng bởi các nhánh sông
Pregel.
• Người ta đã xây 7 cây cầu để nối 4 vùng
• Hỏi có thể xuất phát tại 1 điểm để đi qua tất cả các cầu, mỗi
chiếc cầu không đi qua nhiều hơn 1 lần rồi trở về điểm xuất
phát?
Toán rời rạc Nguyễn Quỳnh Diệp 56
XÂY DỰNG CHU TRÌNH EULER
THUẬT TOÁN : Xây dựng chu trình Euler
Procedure Euler (G: đa đồ thị liên thông với tất cả các đỉnh bậc
chẵn)
C := chọn 1 chu trình bất kì
H := G đã xóa đi cạnh của C
while H còn các cạnh
begin
C’ = chu trình trong H có đi qua đỉnh trong C
H := H xóa đi cạnh của C’ và đỉnh treo
C := C cộng thêm C’ chèn vào tại một đỉnh thích hợp
end
{ chu trình C là chu trình Euler}
Toán rời rạc Nguyễn Quỳnh Diệp 57
XÂY DỰNG CHU TRÌNH EULER
Ví dụ 2: Tìm chu trình Euler của đồ thị sau?
Toán rời rạc Nguyễn Quỳnh Diệp 58
XÂY DỰNG CHU TRÌNH EULER
Giải:
• Chọn C = chu trình {a, f, c, b, a}
• H = các cạnh {c,d}, {c, e}, {e, d}
• C’ = chu trình {c, d, e, c}
• H =
• C: = C C’={a, f, c, b, a} { c, d, e, c} =
{a, f, c, d, e, c, b, a}
• Chu trình Euler là {a,f,c,d,e,c,b,a}
Toán rời rạc Nguyễn Quỳnh Diệp 59
ĐƯỜNG ĐI EULER
Định lí 2:
Một đa đồ thị liên thông có đường đi Euler nhưng không có
chu trình Euler nếu và chỉ nếu nó có đúng hai đỉnh bậc lẻ.
Ví dụ 3: Đồ thị nào có đường đi Euler?
Toán rời rạc Nguyễn Quỳnh Diệp 60
ĐA ĐỒ THỊ CÓ HƯỚNG
• Đa đồ thị có hướng có chu trình Euler nếu và chỉ nếu đồ thị là
liên thông yếu đồng thời bậc vào và bậc ra của mỗi đỉnh là
bằng nhau
• Đa đồ thị có hướng không có đỉnh cô lập, có đường đi Euler
nhưng không có chu trình Euler nếu và chỉ nếu đồ thị là liên
thông yếu đồng thời bậc vào và bậc ra của mỗi đỉnh là bằng
nhau, trừ hai đỉnh, một đỉnh có bậc vào lớn hơn bậc ra 1 đơn
vị, đỉnh kia có bậc ra lớn hơn bậc vào 1 đơn vị.
Toán rời rạc Nguyễn Quỳnh Diệp 61
BÀI TẬP
. Bài 8: Xác định các đồ thị sau có chu trình Euler, đường đi Euler?
Nếu có hãy chỉ ra chu trình, đường đi Euler
62
Toán rời rạc Nguyễn Quỳnh Diệp 62
ĐƯỜNG ĐI VÀ CHU TRÌNH HAMILTON
Trò chơi đố vui của William Rowan Hamilton
Toán rời rạc Nguyễn Quỳnh Diệp 63
ĐƯỜNG ĐI VÀ CHU TRÌNH HAMILTON
Trò chơi đố vui của William Rowan Hamilton
Toán rời rạc Nguyễn Quỳnh Diệp 64
ĐƯỜNG ĐI VÀ CHU TRÌNH HAMILTON
Định nghĩa 2:
• Đường đi x0, x1,...,xn trong đồ thị G(V, E) được gọi là đường đi
Hamilton nếu V= {x0, x1,..., xn-1 ,xn } và xi xj, 0 i < j n
• Chu trình x0, x1,...,xn, x0 trong đồ thị G được gọi là chu trình
Hamilton nếu x0, x1,...,xn là đường đi Hamilton.
Ví dụ 1: Đồ thị nào có chu trình Hamilton?
Toán rời rạc Nguyễn Quỳnh Diệp 65
ĐƯỜNG ĐI VÀ CHU TRÌNH HAMILTON
Định lí 3:
ĐỊNH LÍ DIRAC. Giả sử G là một đơn đồ thị liên thông với n
đỉnh, trong đó n 3, G có chu trình Hamilton nếu bậc của mỗi
đỉnh ít nhất bằng n/2.
Định lí 4:
ĐỊNH LÍ ORE. Nếu G là một đơn đồ thị n đỉnh, trong đó n 3,
sao cho deg(u) + deg(v) n với mọi cặp đỉnh không liền kề u và v,
khi đó G có chu trình Hamilton.
Cả hai định lí trên là các điều kiện đủ để trong một đơn đồ
thị liên thông có tồn tại chu trình Hamilton
Toán rời rạc Nguyễn Quỳnh Diệp 66
BÀI TẬP
. Bài 9: Xác định các đồ thị sau có chu trình và đường đi Hamilton?
67
Toán rời rạc Nguyễn Quỳnh Diệp 67
5.6. BÀI TOÁN ĐƯỜNG ĐI NGẮN NHẤT
Toán rời rạc Nguyễn Quỳnh Diệp 68
ĐỒ THỊ CÓ TRỌNG SỐ
Đồ thị có trọng số là đồ thị mà mỗi cạnh của nó được gán một số
(nguyên hoặc thực) gọi là trọng số của cạnh.
2534
KHOẢNG CÁCH
1855 722
957
349 2451
1090
Toán rời rạc Nguyễn Quỳnh Diệp 69
ĐỒ THỊ CÓ TRỌNG SỐ
Ví dụ:
4:05
THỜI GIAN BAY
0:50
2:55 1:50
2:10
2:20
1:15 2:00 3:50
2:45
Toán rời rạc Nguyễn Quỳnh Diệp 70
ĐỒ THỊ CÓ TRỌNG SỐ
Bài toán liên quan tới đồ thị có trọng số:
• Xác định đường đi ngắn nhất giữa hai đỉnh của một mạng
• Tìm đường đi có chi phí rẻ nhất
• Tìm đường đi có thời gian trả lời nhanh nhất cho một cuộc
truyền thông giữa các máy tính
Toán rời rạc Nguyễn Quỳnh Diệp 71
THUẬT TOÁN TÌM ĐƯỜNG ĐI NGẮN NHẤT
• Do E.Dijkstra nhà toán học người Hà Lan đề xuất năm 1959
• Thực hiện tìm độ dài của đi ngắn nhất từ a tới đỉnh thứ nhất, độ
dài của đường đi ngắn nhất tới đỉnh thứ 2... cho tới đỉnh z
Toán rời rạc Nguyễn Quỳnh Diệp 72
THUẬT TOÁN TÌM ĐƯỜNG ĐI NGẮN NHẤT
Ví dụ: Tìm đường đi ngắn nhất từ s đến t
tìm đường đi
ngắn nhất từ s đến t
• Tìm độ dài của đường đi ngắn nhất từ s tới các đỉnh kế tiếp cho
tới khi đạt tới đỉnh t
Toán rời rạc Nguyễn Quỳnh Diệp 73
THUẬT TOÁN TÌM ĐƯỜNG ĐI NGẮN NHẤT
Ví dụ:
Toán rời rạc Nguyễn Quỳnh Diệp 74
THUẬT TOÁN TÌM ĐƯỜNG ĐI NGẮN NHẤT
• Đường đi ngắn nhất là: s b d t
• Độ dài đường đi ngắn nhất là: 6
Toán rời rạc Nguyễn Quỳnh Diệp 75
THUẬT TOÁN TÌM ĐƯỜNG ĐI NGẮN NHẤT
Ví dụ:
Toán rời rạc Nguyễn Quỳnh Diệp 76
THUẬT TOÁN TÌM ĐƯỜNG ĐI NGẮN NHẤT
Toán rời rạc Nguyễn Quỳnh Diệp 77
THUẬT TOÁN TÌM ĐƯỜNG ĐI NGẮN NHẤT
THUẬT TOÁN : Thuật toán Dijkstra
Procedure Dijkstra(G: đa đồ thị liên thông có trọng số dương)
{G có các đỉnh a = v0, v1, v2..., vn = z và trọng số w(vi, vj), với w(vi, vj) = nếu
{vi,vj} không có cạnh trong G}
L(a) := 0
for i :=1 to n L(vi) =
S :=
while z S
begin
u := đỉnh S có nhãn L(u) nhỏ nhất
S := S {u}
for tât cả các đỉnh v không thuộc S
if L(u) + w(u,v) < L(v) then L(v) := L(u) + w(u,v)
end { L(z) = độ dài đường đi ngắn nhất từ a tới z}
Toán rời rạc Nguyễn Quỳnh Diệp 78
Video: Tìm đường đi ngắn nhất từ A đến G
Toán rời rạc Nguyễn Quỳnh Diệp 79
THUẬT TOÁN TÌM ĐƯỜNG ĐI NGẮN NHẤT
Ví dụ: tìm đường đi ngắn nhất từ s đến t
s a b c d t
s ퟒ ∞ ∞ ∞
ma trận trọng số a ퟒ ∞ ∞
W = b ∞
c ∞
d ∞ ∞
t ∞ ∞ ∞
Toán rời rạc Nguyễn Quỳnh Diệp 80
THUẬT TOÁN TÌM ĐƯỜNG ĐI NGẮN NHẤT
u S v S s a b c d t
s, a, b, c, d, t 0
s, s a, b, c, d, t - [4, s] [2, s]*
L(s)=0
b, s, b a, c, d, t - [3, b]* - [10,b] [12,b]
L(b)=2
a, s,b,a c, d, t - - - [8,a]* [12,b]
L(a)=3
c, s, b, a, c d, t - - - - [10,c]* [14,c]
L(c)=8
d, s, b, a, c, d, t - - - - - [13,d]*
L(d)=10
t, s, b, a, c, d, t - - - - - -
L(t)=13
Đường đi ngắn nhất: s b a c d t, độ dài = 13
Toán rời rạc Nguyễn Quỳnh Diệp 81
BÀI TẬP
. Bài 10: Tìm độ dài đường đi ngắn nhất giữa a và z trong đồ thị sau:
82
Toán rời rạc Nguyễn Quỳnh Diệp 82
BÀI TẬP
. Bài 11: Tìm độ dài đường đi ngắn nhất giữa a và z trong đồ thị sau:
b 5 d 5 f
4 7
3
a 2 1 2 z
3 4
c 6 e 5 g
83
Toán rời rạc Nguyễn Quỳnh Diệp 83
84
Nguyễn Quỳnh DiệpFile đính kèm:
 bai_giang_toan_roi_rac_chuong_5_do_thi_nguyen_quynh_diep.pdf
bai_giang_toan_roi_rac_chuong_5_do_thi_nguyen_quynh_diep.pdf

