Bài giảng Toán rời rạc - Chương 5: Đại số Boole & cấu trúc mạch logic - Bùi Thị Thủy

 TOÁN RỜI RẠC 
(DISCRETE MATHEMATICS) 
 Bùi Thị Thủy 
 Đặng Xuân Thọ 
 Support 
2 
  TS. Đặng Xuân Thọ 
  Mobile: 091.2629.383 
  Email: thodx@hnue.edu.vn 
  Website:  
 Toán rời rạc - ĐHSPHN 
 NỘI DUNG 
3 
  Chương 1. Logic mệnh đề 
  Chương 2. Lý thuyết tập hợp 
  Chương 3. Một số công thức tổ hợp 
  Chương 4. Suy luận và kiểm chứng chương trình 
  Chương 5. Đại số Boole và cấu trúc mạch logic 
  Chương 6. Thuật toán 
  Chương 7. Lý thuyết đồ thị 
 Toán Rời Rạc - ĐHSPHN 
 Chương 5. Đại Số Boole & Cấu Trúc 
 Mạch Logic 
4 
  Giúp tính toán các biểu thứ logic trên bảng giá 
 trị chân lý 0 và 1 cho ra đời một ngành toán 
 học mới là đại số Boole. 
  Biểu thức Boole và hàm Boole 
  Xác định biểu thức Boole của hàm Boole 
  Sơ đồ mạch logic 
 Toán Rời Rạc - ĐHSPHN 
5 Biểu thức Boole và hàm Boole 
 Toán Rời Rạc - ĐHSPHN 
 Biểu thức Boole & hàm Boole 
6 
  Định nghĩa. Đại số Boole là một tập hợp B với 3 
 phép toán: phép lấy phần bù (-), phép lấy tổng Boole 
 (+), và phép nhân ( ). Tập hợp B có 2 phần tử đặc 
 biệt là 0 và 1 sao cho các đẳng thức sau thỏa mãn: 
  b.1 = b + 0 = b, b B (luật đồng nhất) 
  b + = 1; b. = 0, b B (luật bù) 
  (x + y) + z = x + (y + z); (x.y).z = x.(y.z) (kết hợp) 
  x + y = y + x; x.y = y.x (giao hoán) 
  x.(y + z) = x.y + x.z; (x.y) + z = (x + z). (y + z) 
 (phân phối) 
 Toán Rời Rạc - ĐHSPHN 
 Biểu thức Boole & hàm Boole 
7 
  Thứ tự thực hiện của các phép tính của đại số 
 Boole như sau: 
 Lấy phần bù > Phép lấy tích > Phép lấy tổng 
  Khi có các dấu ngoặc, thực hiện theo thứ tự 
 thông thường là ngoặc trong cùng được thực 
 hiện trước. 
  Phép lấy phần bù, phép nhân, và phép tổng 
 của đại số Boole tương ứng với các toán tử 
 logic: phần bù, ⋀, và ⋁. 
 Toán Rời Rạc - ĐHSPHN 
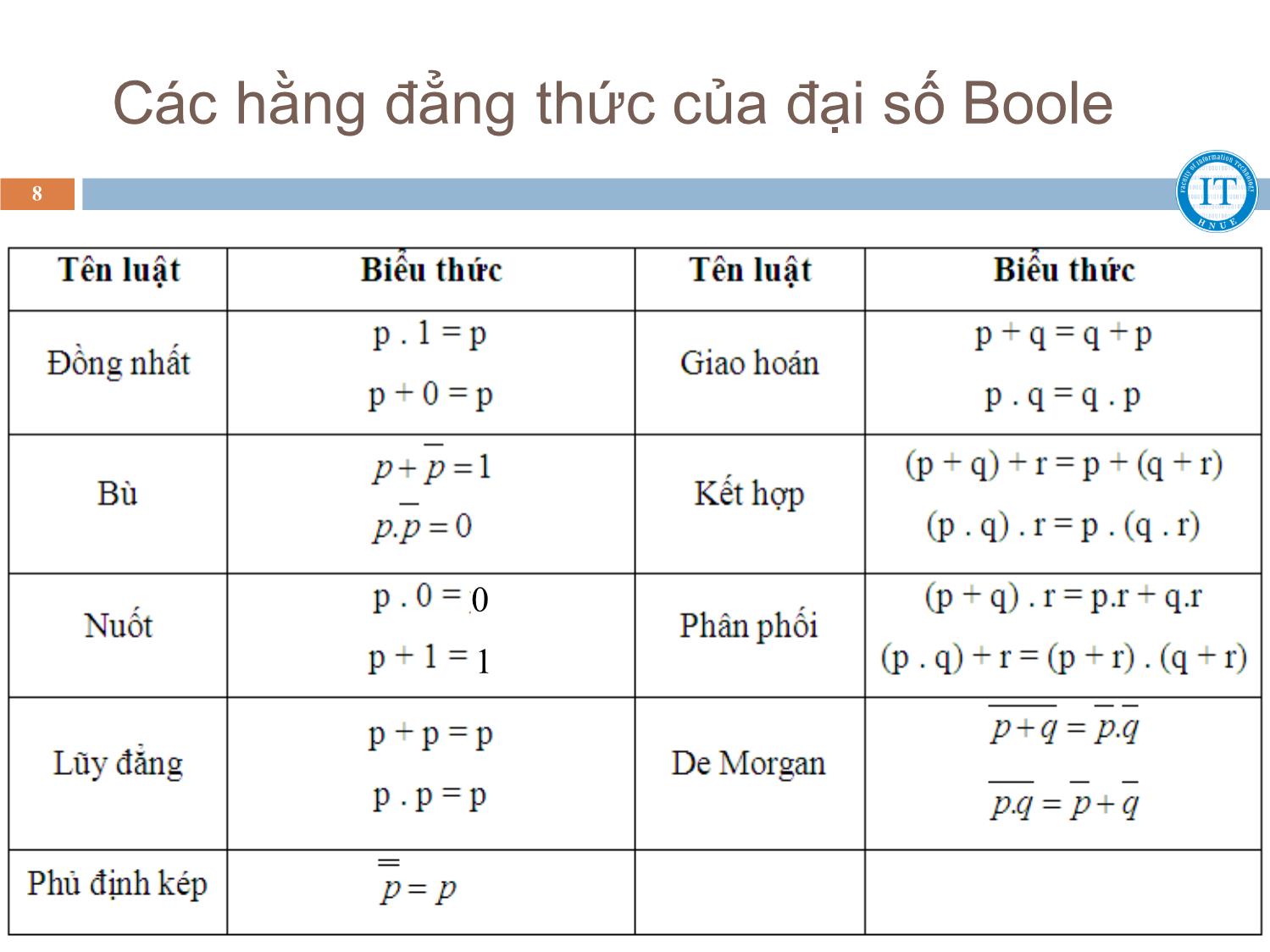
 Các hằng đẳng thức của đại số Boole 
8 
 0 
 1 
 Các hằng đẳng thức của đại số Boole 
9 
 Ví dụ: Tính giá trị của x x(1 y )
 Ta có: 
 x ( x .1 x . y )
 x (.) x x y
 ().x x x y
 1.xy
 1
 Toán Rời Rạc - ĐHSPHN 
 Biểu thức Boole & hàm Boole 
10 
  Một hàm số Boole F với n biến x1, x2, , xn 
 được kí hiệu F(x1, x2, , xn) là một ánh xạ 
 f : {0, 1}n {0, 1} 
  Hàm Boole có thể được mô tả bằng lời hoặc 
 dùng bảng tương tự bảng logic toán. 
  Ví dụ: hàm F(x,y) sau x y F(x,y) 
 1 1 1 
 1 0 0 
 0 1 0 
 0 0 0 
 Toán Rời Rạc - ĐHSPHN 
 Biểu thức boole & hàm boole 
11 
  Hai hàm boole F(x1,x2,,xn) và G(x1,x2,,xn) 
 là hai hàm Boole bằng nhau nếu 
 F(x1, x2, , xn) = G(x1, x2, , xn) 
 cho mọi giá trị của các biến. 
 Toán Rời Rạc - ĐHSPHN 
12 Xác định biểu thức Boole của hàm Boole 
 Toán Rời Rạc - ĐHSPHN 
 Xác định biểu thức Boole của hàm Boole 
13 
  Quy tắc 1: Khai triển các bảng thành 
 các bảng sơ cấp x1 x2 F1(x1,x2) 
 1 1 1 
 x1 x2 F(x1,x2) 1 0 0 
 1 1 1 0 1 0 
 1 0 0 0 0 0 
 0 1 0 x1 x2 F2(x1,x2) 
 0 0 1 1 1 0 
 1 0 0 
 0 1 0 
퐹 1, 2 = 퐹1 1, 2 + 퐹2( 1, 2) 0 0 1 
 Xác định biểu thức Boole của hàm Boole 
14 
  Quy tắc 1 
  Nếu hàm F(x1, x2, , xn) nhận duy nhất giá trị 1 
 tại (a1,a2, ,an) và 0 tại mọi giá trị khác của 
 (x1,x2, , xn) thì ta có: 
 F(x1, x2, , xn) = y1y2yn 
 quy ước: yi = xi nếu ai = 1 
 yi = 푖 nếu ai = 0 
 Toán Rời Rạc - ĐHSPHN 
 Xác định biểu thức Boole của hàm Boole 
 15 
 
 Quy tắc 1 x1 x2 F1(x1,x2) 
  Ví dụ: 1 1 1 
 퐹1 1, 2 = 1 2 1 0 0 
 0 1 0 
 0 0 0 
퐹 1, 2 = 1 2+ 1 2 
 x1 x2 F2(x1,x2) 
 1 1 0 
 1 0 0 
 퐹2 1, 2 = 1 2 
 0 1 0 
 0 0 1 
 Toán Rời Rạc - ĐHSPHN 
 Xác định biểu thức Boole của hàm Boole 
16 
  Quy tắc 2: Khai triển các bảng thành 
 các bảng sơ cấp x1 x2 G1(x1,x2) 
 1 1 1 
 x1 x2 F(x1,x2) 1 0 0 
 1 1 1 0 1 1 
 1 0 0 = × 0 0 1 
 0 1 0 x1 x2 G2(x1,x2) 
 0 0 1 1 1 1 
 1 0 1 
 0 1 0 
퐹 1, 2 = 1 1, 2 × 2( 1, 2) 0 0 1 
 Xác định biểu thức Boole của hàm Boole 
17 
  Quy tắc 2 
  Nếu hàm F(x1, x2, , xn) nhận duy nhất giá trị 0 
 tại (a1,a2, ,an) và 1 tại mọi giá trị khác của 
 (x1,x2, , xn) thì ta có: 
 F(x1, x2, , xn) = y1 + y2 + + yn 
 quy ước: yi = 푖 nếu ai = 1 
 yi = xi nếu ai = 0 
 Toán Rời Rạc - ĐHSPHN 
 Xác định biểu thức Boole của hàm Boole 
 18 
 
 Quy tắc 2 x1 x2 G1(x1,x2) 
  Ví dụ: 1 1 1 
 1 1, 2 = 1 + 2 1 0 0 
 0 1 1 
 0 0 1 
퐹 1, 2 = 
( 1 + 2)( 1 + 2) x1 x2 G2(x1,x2) 
 1 1 1 
 1 0 1 
 2 1, 2 = 1 + 2 
 0 1 0 
 0 0 1 
 Toán Rời Rạc - ĐHSPHN 
 Luyện tập 
19 
  Tìm các hàm chỉ nhận giá trị 1 tại giá trị sau: 
 a) (x, y, z) = (0, 0, 1) 
 b) (x, y, z) = (0, 1, 1) 
 c) (x, y, z) = (0, 1, 0) 
  Tìm các hàm chỉ nhận giá trị 0 tại giá trị sau: 
 a) (x, y, z) = (0, 0, 1) 
 b) (x, y, z) = (0, 1, 1) 
 c) (x, y, z) = (0, 0, 0) 
 Toán Rời Rạc - ĐHSPHN 
20 Sơ đồ mạch logic 
 Toán Rời Rạc - ĐHSPHN 
 Các cổng logic cơ bản 
21 
  Các mạch chúng ta nghiên cứu ở đây không 
 có khả năng nhớ, nghĩa là giá trị của nó chỉ 
 phụ thuộc vào giá trị đầu vào mà không phụ 
 thuộc vào trạng thái của mạch lúc đó. 
  Các mạch như vậy gọi là các mạch tổ hợp. 
  Các phần tử cơ bản của các mạch được gọi là 
 các cổng. 
 Toán Rời Rạc - ĐHSPHN 
 Các cổng logic cơ bản 
22 
 x x
  Cổng NOT 
 x xy 
  Cổng OR 
 y
 xy
  Cổng AND 
 Toán Rời Rạc - ĐHSPHN 
 Tổ hợp các cổng và thiết kế mạch 
23 
  Khi lập tổ hợp các mạch phức hợp, ta sử dụng 
 các cổng cơ bản. 
  Có thể dùng chung đầu vào cho các cổng. 
  Ví dụ: + 
 x xy
 y
 xy xy
 x xy
 Toán Rời Rạc - ĐHSPHN 
 Luyện tập 
24 
  Dựng các mạch có đầu ra là các hàm Boole 
 sau: 
 a) + 
 b) 
 c) + + 
 d) + 
 e) + + + + 
 Toán Rời Rạc - ĐHSPHN 
THANK YOU!