Bài giảng Toán rời rạc - Chương 3: Phép quy nạp và đệ quy - Nguyễn Quỳnh Diệp

 CHƯƠNG 3
 PHÉP QUY NẠP VÀ 
 ĐỆ QUY
 Nguyễn Quỳnh Diệp
 diepnq@tlu.edu.vn
File Bài giảng: goo.gl/Y3cpLF hoặc goo.gl/TYxXQD
 1
 Nguyễn Quỳnh Diệp
NỘI DUNG
 • Quy nạp toán học
 • Đệ quy
 Toán rời rạc Nguyễn Quỳnh Diệp 2
 3.1. QUY NẠP TOÁN HỌC
Toán rời rạc Nguyễn Quỳnh Diệp 3
QUY NẠP TOÁN HỌC
 Các phương pháp chứng minh cơ sở:
 • Chứng minh trực tiếp
 • Chứng minh gián tiếp
 • Chứng minh phản chứng
 • Chứng minh từng trường hợp
 • Chứng minh tương đương
 Toán rời rạc Nguyễn Quỳnh Diệp 4
QUY NẠP TOÁN HỌC
 Chứng minh bằng quy nạp
 • Là kĩ thuật sử dụng để chứng minh các mệnh đề phổ
 quát trên tập các số nguyên dương, x P(x) với x 
 Z+.
 • Bao gồm 2 bước:
 1) Bước cơ sở: chỉ ra mệnh đề P(1) là đúng
 2) Bước quy nạp: Chứng minh mệnh đề kéo theo
 P(k) P(k+1) là đúng với mọi số nguyên
 dương k
 Toán rời rạc Nguyễn Quỳnh Diệp 5
QUY NẠP TOÁN HỌC
Ví dụ 1: Chứng minh tổng n số nguyên dương lẻ đầu tiên là n2
 1 + 3 + 5 + 7 +  + 2푛 − 1 = 푛2
 • Bước cơ sở: P(1) luôn đúng vì 1 = 12
 • Bước quy nạp: giả định P(k) đúng với n= k, tức là:
 1 + 3 + 5 + 7 +  + 2 − 1 = 2
 Ta phải chứng minh P đúng với n=k+1.
 Tức là: P(k+1) = 1 + 3 + 5 + 7 +  + 2 − 1 + 2 + 1 = ( + 1)2
 VT = 2 + 2 + 1 = ( + 1)2=VP
 • Vậy P(n) đúng với mọi n nguyên dương
 Toán rời rạc Nguyễn Quỳnh Diệp 6
QUY NẠP TOÁN HỌC
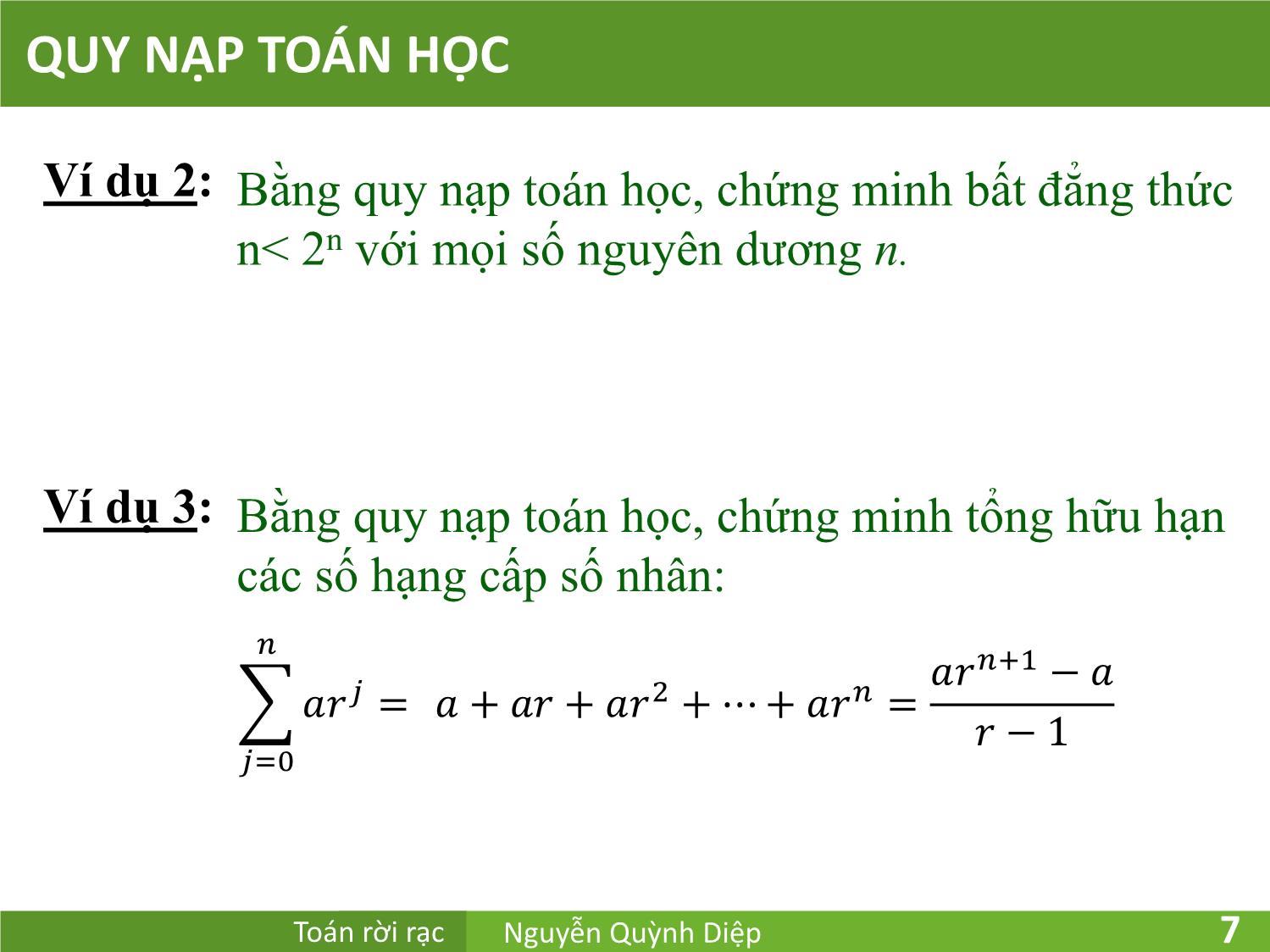
 Ví dụ 2: Bằng quy nạp toán học, chứng minh bất đẳng thức
 n< 2n với mọi số nguyên dương n.
 Ví dụ 3: Bằng quy nạp toán học, chứng minh tổng hữu hạn
 các số hạng cấp số nhân:
 푛
 푛+1 − 
 푗 = + + 2 + ⋯ + 푛 =
 − 1
 푗=0
 Toán rời rạc Nguyễn Quỳnh Diệp 7
BÀI TẬP
 . Bài 1: Tìm công thức tính tổng:
 1 1 1
 + + ⋯ +
 1.2 2.3 푛. (푛 + 1)
 Dùng quy nạp toán học để chứng minh kết quả vừa tìm
 được.
. Bài 2: Chứng tỏ rằng với n là số nguyên dương ta có:
 12 + 22 + 32 +... + n2 = n(n+1)(2n+1)/6 
 9
 Toán rời rạc Nguyễn Quỳnh Diệp
 3.2. ĐỊNH NGHĨA ĐỆ QUY
Toán rời rạc Nguyễn Quỳnh Diệp 10
ĐỆ QUY
 • Phép đệ quy: Định nghĩa đối tượng qua chính nó
 Toán rời rạc Nguyễn Quỳnh Diệp 11
ĐỆ QUY
 Định nghĩa đệ quy
 • Là định nghĩa một dãy, tập hợp bằng cách định nghĩa các 
 số hạng của dãy, tập hợp thông qua các số hạng trước đó
 Các hàm được định nghĩa bằng đệ quy:
 1) Bước cơ sở: cho giá trị của hàm tại 0
 2) Bước đệ quy: Cho quy tắc tính giá trị của nó tại
 một số nguyên n từ các giá trị nhỏ hơn n
 Toán rời rạc Nguyễn Quỳnh Diệp 12
ĐỆ QUY
 Ví dụ: Định nghĩa đệ quy của hàm giai thừa F(n) = n!
 • Bước cơ sở: F(0) = 0! = 1
 • Bước đệ quy: 
 - F(1) = 1*F(0) = 1.1 = 1
 - F(2) = 2*F(1) = 2.1 = 2
 - F(3) = 3*F(2) = 3.2 = 6
 - F(n) = n*F(n-1)
 Toán rời rạc Nguyễn Quỳnh Diệp 13
ĐỆ QUY
 Định nghĩa 1:
 Các số Fibonaci f0, f1, f2... được định nghĩa bởi các
 phương trình: f0=0, f1= 1 và fn = fn-1 + fn-2
 trong đó n= 2, 3, 4,...
 Ví dụ:
 • Tìm các số hạng f2 ,f3 ,f4 ,f5 ,f6 của dãy Fibonacci
 Toán rời rạc Nguyễn Quỳnh Diệp 14
 BÀI TẬP
 . Bài 3: Hãy định nghĩa đệ quy của hàm sau:
 a) an, với n 0, n nguyên
 풏
 b) 풌= 풌
. Bài 4: Hãy cho định nghĩa đệ quy của dãy {an} , n = 1, 
 2,... nếu
 a) an = 6n b) an = 2n + 1
 n
 c) an = 10 d) an = 5
 15
 Toán rời rạc Nguyễn Quỳnh Diệp
CÁC TẬP HỢP ĐƯỢC ĐỊNH NGHĨA ĐỆ QUY
 Giống như định nghĩa bằng đệ quy đối với các hàm, định
 nghĩa đệ quy cho tập hợp cũng gồm 2 phần: bước cơ sở và
 bước đệ quy.
 - Trong bước CƠ SỞ: người ta cho các phần tử xuất phát.
 - Trong bước ĐỆ QUYy: người ta cho quy tắc để tạo ra các
 phần tử mới từ các phần tử đã biết
 Toán rời rạc Nguyễn Quỳnh Diệp 16
CÁC TẬP HỢP ĐƯỢC ĐỊNH NGHĨA ĐỆ QUY
Ví dụ: Cho tập S được định nghĩa như sau:
 • BƯỚC CƠ SỞ: 3 S
 • BƯỚC ĐỆ QUY: Nếu x S và y S thì x + y S
 Hãy chỉ ra các phần tử của tập S sau 3 lần đệ quy
 Toán rời rạc Nguyễn Quỳnh Diệp 17
CÁC THUẬT TOÁN ĐỆ QUY
 Định nghĩa 1:
 Một thuật toán được gọi là đệ quy, nếu nó 
 giải một bài toán bằng cách rút gọn liên tiếp 
 bài toán đó tới giai đoạn của chính bài toán 
 ban đầu nhưng có dữ liệu đầu vào nhỏ hơn
 Toán rời rạc Nguyễn Quỳnh Diệp 20
CÁC THUẬT TOÁN ĐỆ QUY
Ví dụ :
 Tìm thuật toán đệ quy tính giá trị an, với 
 a là số thực khác 0 và n là số nguyên 
 không âm.
 THUẬT TOÁN : Thuật toán đệ quy tính an
 Procedure power(a: số thực khác 0; n: nguyên không âm)
 if n = 0 then 
 power(a, n) := 1
 else power(a,n) := a.power(a, n-1)
 Toán rời rạc Nguyễn Quỳnh Diệp 21
CÁC THUẬT TOÁN ĐỆ QUY
 Ví dụ 1: Biểu diễn thuật toán tính ước chung lớn nhất của 
 hai số a,b như một thủ tục đệ quy.
 Ví dụ 2: Biểu diễn thuật toán tìm kiếm tuyến tính và tìm 
 kiếm nhị phân như một thủ tục đệ quy.
 Toán rời rạc Nguyễn Quỳnh Diệp 22
CÁC THUẬT TOÁN ĐỆ QUY
 Tìm kiếm tuyến tính
 THUẬT TOÁN : Thuật toán đệ quy tìm kiếm tuyến tính
 Procedure search (i, j, x)
 if ai = x then 
 location := i
 else if 푖 = 푗 then 
 location := 0
 else
 search(i+1, j, x)
 Toán rời rạc Nguyễn Quỳnh Diệp 23
CÁC THUẬT TOÁN ĐỆ QUY
 Tìm kiếm nhị phân
 THUẬT TOÁN : Thuật toán đệ quy tìm kiếm nhị phân
 Procedure binary search (i, j, x)
 m := (i+j)/2 
 if x = ai then
 location := m
 else if (퐱 < và i < m ) then 
 binary search(x,i, m-1)
 else if ( x > am và m < j) then
 binary search(x,m+1, j)
 else
 location :=0
 Toán rời rạc Nguyễn Quỳnh Diệp 24
BÀI TẬP
. Bài 4: Xây dựng thuật toán đệ quy tính n!
. Bài 5: Xây dựng thuật toán đệ quy tính các số fibonacci
 25
 Toán rời rạc Nguyễn Quỳnh Diệp
BÀI TẬP
 . Bài 6: Hãy đưa thuật toán đệ quy tìm tổng n số nguyên 
 dương lẻ đầu tiên.
. Bài 7: Số hạng thứ n được định nghĩa như sau: a0 = 1, 
 a1=2 và an= an-1.an-2, với n = 2,3, 4...
 a) Hãy định nghĩa hàm đệ quy để tính an
 b) Xây dựng thuật toán đệ quy để tính an
 26
 Toán rời rạc Nguyễn Quỳnh Diệp
 27
Nguyễn Quỳnh Diệp