Bài giảng Toán rời rạc - Chương 3: Một số công thức tổ hợp - Bùi Thị Thủy

 TOÁN RỜI RẠC 
(DISCRETE MATHEMATICS) 
 Bùi Thị Thủy 
 Đặng Xuân Thọ 
 Support 
2 
  Full name: Đặng Xuân Thọ 
  Mobile: 091.2629.383 
  Email: thodx@hnue.edu.vn 
  Website:  
 Toán Rời Rạc - ĐHSPHN 
 NỘI DUNG 
3 
  Chương 1. Logic mệnh đề 
  Chương 2. Lý thuyết tập hợp 
  Chương 3. Một số công thức tổ hợp 
  Chương 4. Suy luận và kiểm chứng chương trình 
  Chương 5. Đại số Boole và cấu trúc mạch logic 
  Chương 6. Thuật toán 
  Chương 7. Lý thuyết đồ thị 
 Toán Rời Rạc - ĐHSPHN 
 Chương 3. Một số công thức tổ hợp 
4 
  “Đánh giá số điện thoại nhiều nhất có thể có 
 trong Hà Nội.” 
  “Xác định số mật khẩu, mỗi mật khẩu gồm 
 sáu, bảy, hoặc tám ký tự; mỗi ký tự có thể chữ 
 hoặc số; mỗi mật khẩu chứa ít nhất một chữ.” 
  Một số công thức tổ hợp 
  Chỉnh hợp 
  Hoán vị 
  Hoán vị trên đường tròn 
   
 Toán Rời Rạc - ĐHSPHN 
5 Cơ sở của phép đếm 
 Toán Rời Rạc - ĐHSPHN 
 Cơ sở của phép đếm 
6 
  Phần này chúng ta chỉ giải quyết xác định lực 
 lượng của tập hợp hữu hạn. 
  Nếu tập hợp A là tập hợp hữu hạn, thì lực 
 lượng của nó là số lượng phần tử của nó, ký 
 hiệu là . 
  Định lý: Nếu Ai (i=1,2,..n) là một phân hoạch 
 푛
 của tập hợp A thì ta có 푖=1 푖 = . 
 Toán Rời Rạc - ĐHSPHN 
 Số phần tử của tích Đêcac 
7 
  Ví dụ: Cho tập hợp A={a,b}. Tìm tất cả các 
 dãy ký tự có ba phần tử được tạo thành từ A? 
  aaa, aab, bbb, bba, abb, baa, aba, bab 
  Định lý: cho trước các tập hợp hữu hạn Ai 
 (i=1,..,k) trong đó tập hợp Ai có đúng ni phần 
 tử. Khi đó tích Đêcac A1 x A2 x  x Ak có đúng 
 n1n2nk phần tử. Nghĩa là: 
 1 × 2 × ⋯ × = 1 × 2 × 
 푛 푛 
  Đặc biệt ta có: = 
 Toán Rời Rạc - ĐHSPHN 
 Số phần tử của tích Đêcac 
8 
  Ví dụ: Có bao nhiêu số tự nhiên có chín chữ 
 số mà trong biểu diễn thập phân của nó không 
 có mặt chữ số nào trong tập hợp {0,3,7,9}? 
  Mỗi số tự nhiên có chín chữ số không được viết 
 bởi các chữ số {0,3,7,9} là một dãy chín kí tự có 
 lặp của tập hợp {1,2,4,5,6,8}. 
 69 
 Toán Rời Rạc - ĐHSPHN 
9 Hai nguyên lý cơ bản 
 Toán Rời Rạc - ĐHSPHN 
 Cơ sở của phép đếm (1/2) 
10 
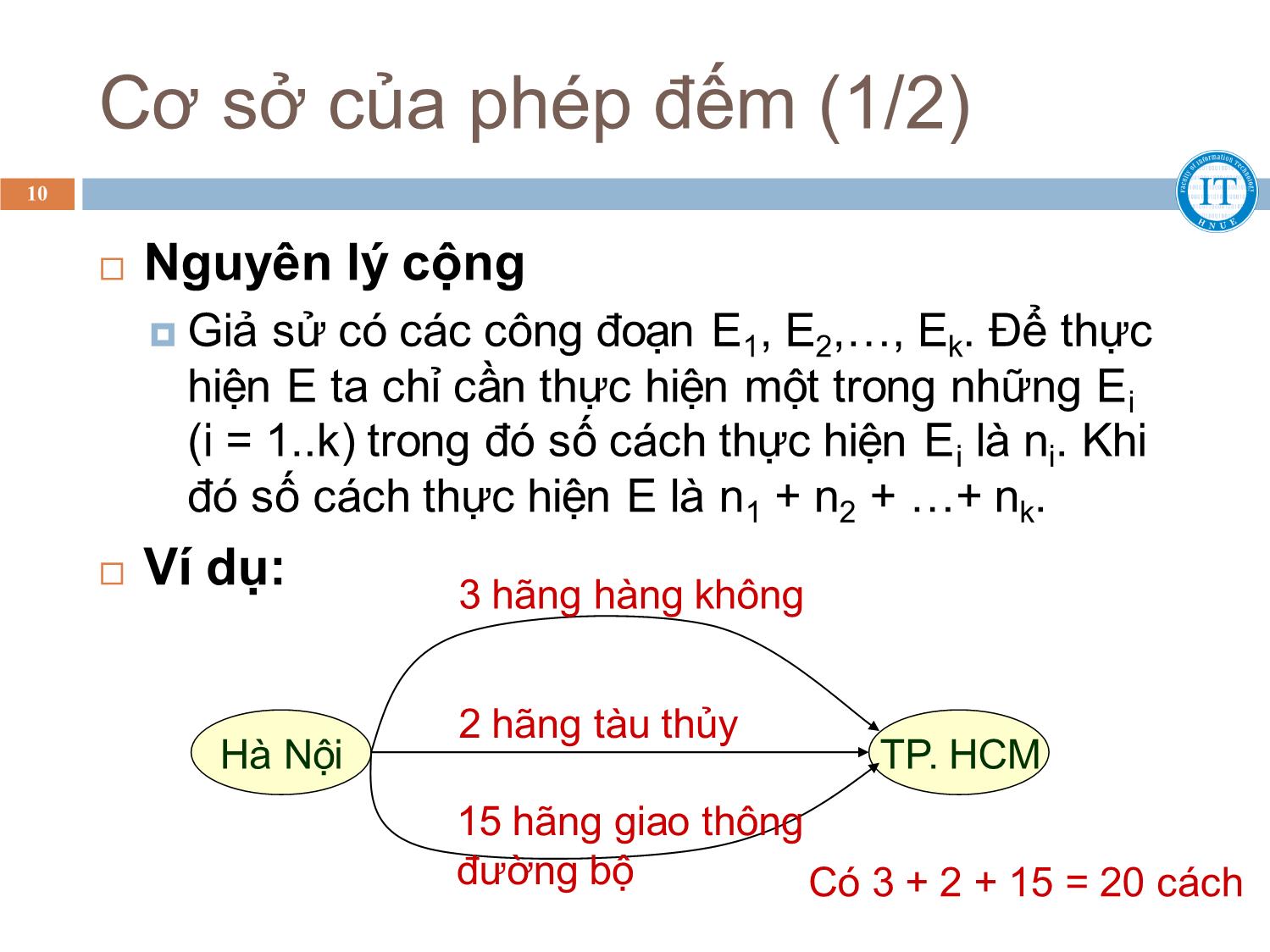
  Nguyên lý cộng 
  Giả sử có các công đoạn E1, E2,, Ek. Để thực 
 hiện E ta chỉ cần thực hiện một trong những Ei 
 (i = 1..k) trong đó số cách thực hiện Ei là ni. Khi 
 đó số cách thực hiện E là n1 + n2 + + nk. 
  Ví dụ: 
 3 hãng hàng không 
 2 hãng tàu thủy 
 Hà Nội TP. HCM 
 15 hãng giao thông 
 đường bộ Có 3 + 2 + 15 = 20 cách 
 Cơ sở của phép đếm (2/2) 
11 
  Nguyên lý nhân 
  Giả sử có công đoạn E được thực hiện lần lượt 
 qua các công đoạn E1, E2, , Ek trong đó số cách 
 thực hiện Ei là ni (i = 1, k). Khi đó số cách thực 
 hiện E là n1 x n2 x  x nk 
  Ví dụ: 
 8 cách 4 cách 
 Hà Nội Đà Nẵng TP. HCM 
 Có 8 * 4 = 32 cách 
 Toán Rời Rạc - ĐHSPHN 
12 Một Số Công Thức Tổ Hợp 
 Toán Rời Rạc - ĐHSPHN 
 Hoán vị 
13 
  Khái niệm. Hoán vị của một tập các đối tượng 
 khác nhau là một cách sắp xếp có thứ tự các 
 đối tượng này. 
  Bài toán. Cho tập A có n phần tử. Hãy tính số 
 các hoán vị khác nhau của tập A. 
  Ví dụ: cho A={a,b,c,d} tìm tất cả các hoán vị có thể có 
 của tập hợp A? 
  Định lý. Số các hoán vị khác nhau của một 
 tập n phần tử là Pn = n! 
 Toán Rời Rạc - ĐHSPHN 
 Hoán vị 
14 
  Ví dụ: Hãy tính số các số sau: 
  Có năm chữ số được viết bởi đúng 5 chữ số 1, 2, 
 3, 4 và 5? 
  Có năm chữ số được viết bởi đúng 5 chữ số 1, 2, 
 3, 4 và 5 trong đó ba chữ số đầu là ba chữ số lẻ, 
 hai chữ số sau là hai chữ số chẵn? 
 Toán Rời Rạc - ĐHSPHN 
 Hoán vị trên đường tròn 
15 
  Ví dụ: Cho tập hợp A = {a,b,c,d}. Tìm tất cả 
 các hoán vị khác nhau của các phần tử của A 
 trên đường tròn? 
 Toán Rời Rạc - ĐHSPHN 
 Hoán vị trên đường tròn 
16 
  Bài toán: Tính số các hoán vị khác nhau của 
 một tập hợp A gồm n phần tử nằm trên một 
 đường tròn? 
  Định lý: Số các hoán vị tròn khác nhau của 
 tập hợp A có n phần tử là Qn = (n – 1)! 
 Toán Rời Rạc - ĐHSPHN 
 Chỉnh hợp 
17 
  Bài toán: Cho tập A có n phần tử và số k≤n 
 (k N). Mỗi dãy độ dài k được xếp bởi các 
 phần tử của tập A trong đó mỗi phần tử có 
 mặt không quá một lần được gọi là một dãy 
 k phần tử không lặp của A. 
  Tính số các dãy đó? 
 Toán Rời Rạc - ĐHSPHN 
 Chỉnh hợp 
18 
  Định lý: Cho trước tập A có n phần tử và một 
 số tự nhiên k ≤ n. Số các dãy k phần tử không 
 lặp của A là: 
  Ví dụ: có bao nhiêu số có 4 chữ số mà trong 
 biểu diễn thập phân của nó không có 2 chữ số 
 nào giống nhau và không có mặt chữ số 
 chẵn? 
 Toán Rời Rạc - ĐHSPHN 
 Chỉnh hợp lặp 
19 
  Cho tập A có n phần tử. Khi đó số dãy gồm k 
 phần tử có lặp thuộc tập A là nk và được gọi là 
 chỉnh hợp lặp chập k của n phần tử. 
  Ví dụ: có bao nhiêu số tự nhiên có 9 chữ số 
 mà trong biểu diễn thập phân của nó không có 
 mặt chữ số nào trong tập hợp {0,1,2,3,4,5}? 
 Toán Rời Rạc - ĐHSPHN 
 Chỉnh hợp với tần số lặp cho trước 
20 
  Định lý: Cho trước một tập hợp A có n phần 
 tử. Số các dãy k phần tử có lặp (k1+k2++kn) 
 và (k=k1++kn) là: 
 k!
 P( k12 , k ,..., kn ) 
 k12! k !... kn !
  Ví dụ: Tính các số tự nhiên có 7 chữ số, trong 
 đó có 3 chữ số 1, 2 chữ số 2 và 2 chữ số 3. 
 Toán Rời Rạc - ĐHSPHN 
 Tổ hợp 
21 
  Tổ hợp chập k của n phần tử là số các tập 
 hợp con k phần tử của một tập n phần tử cho 
 trước (không có thứ tự). 
  Ví dụ: Cho tập hợp A={a,b,c,d}. Tìm tất cả các 
 tập hợp hai phần tử của A? 
  {a,b}; {a,c}; {a,d}; {b,c}; {b,d}; {c,d} 
  Định lý. Số tập hợp con k phần tử của một tập 
 A có n phần tử cho trước là: 
 Toán Rời Rạc - ĐHSPHN 
 Tổ hợp 
22 
  Ví dụ 1. Có bao nhiêu cách tuyển 5 trong số 
 10 cầu thủ của một đội bóng để đi thi đấu tại 
 một trường khác? 
  Ví dụ 2. Trong 10 cầu thủ trên, có 3 cầu thủ 
 nữ. Hỏi có bao nhiêu cách chọn 5 cầu thủ đi 
 thi đấu trong đó có 2 cầu thủ nữ. 
 Toán Rời Rạc - ĐHSPHN 
 Luyện tập 
23 
 1. Có bao nhiêu số tự nhiên có 5 chữ số đôi một 
 khác nhau? 
 2. Có bao nhiêu máy điện thoại có 6 chữ số? 
 Và trường hợp 6 chữ số đôi một khác nhau? 
 3. Cho A={1,2,3,4,5,6,7}. Có bao nhiêu số tự 
 nhiên có 5 chữ số lấy từ A sao cho: 
  Có chữ số đầu là 3 
  Không tận cùng bằng chữ số 4 
  Cứ 2 chữ số kề nhau là khác nhau 
  Không bắt đầu bằng 123 
 Luyện tập 
24 
 4. Một lớp học có 40 học sinh với 25 nam và 15 
 nữ. Có mấy cách chọn 4 học sinh sao cho: 
 a. Chọn nam, nữ tùy ý 
 b. Chọn 2 nam và 2 nữ 
 c. Tính xác suất để chọn ít nhất một nữ 
 5. Tìm số đường chéo của đa giác lồi có n cạnh. 
 (Đa giác lồi là đa giác có tính chất kéo dài bất kỳ cạnh 
 nào đều không cắt đa giác. Khi đó 2 đỉnh bất kỳ nối 
 lại, được hoặc cạnh hoặc đường chéo.) 
 Toán Rời Rạc - ĐHSPHN 
 Luyện tập 
25 
 6. Từ tập A = {0,1,2,3,4,5} lập được bao nhiêu số tự 
 nhiên có 8 chữ số sao cho: 
 - chữ số 2 có mặt 3 lần 
 - mỗi chữ số còn lại có mặt 1 lần 
 7. Xét tam giác có đỉnh lấy từ một đa giác lồi có 20 
 cạnh. 
 a. Có bao nhiêu tam giác nói trên? 
 b. Tính xác suất để chọn được tam giác có đúng 1 cạnh 
 chung với đa giác? 
 c. Có bao nhiêu tam giác có đúng 2 cạnh chung với đa giác? 
 d. Tính xác suất để chọn được tam giác không có cạnh 
 chung với đa giác? 
 Toán Rời Rạc - ĐHSPHN 
26 Khai triển lũy thừa của đa thức 
 Toán Rời Rạc - ĐHSPHN 
 Hệ số tam giác Pascal 
27 
 (a+b)2 = a2 + 2ab + b2 
 (a+b)3 = a3 + 3a2b + 3ab2 + b3 
 (a+b)4 = a4 + 4a3b + 6a2b2 + 4ab3 + b4 
 1 2 1 
 1 3 3 1 
 1 4 6 4 1 
 Toán Rời Rạc - ĐHSPHN 
 Nhị thức Newton 
28 
  Định lý. Cho mỗi số tự nhiên n 1 ta có: 
 n
 n k n k k
 a b Cn a b
 k 0
 0 n 1 n-1 2 2 n-2 n-1 n-1 n n
 = C nb + C nab + C na b +  + C na b + C na
 Toán Rời Rạc - ĐHSPHN 
 Nhị thức Newton 
29 
  Tính chất: 
 k n k
 1.CCnn 
 k k k 1
 2.CCCn n 11 n
 k k 1 k 1 k 1
 3.CCCCn n 12 n ... n k
 Toán Rời Rạc - ĐHSPHN 
 Ví dụ 
30 
 0 1 n
  Ví dụ 1: Tính A = C n + C n +  + C n 
 n n
 n k k n k k k
 x 1 Cn x 1 Cn x
 k 0 k 0
 0 1 2 2 n-1 n-1 n n
 = C n + C nx + C nx +  + C nx + C nx 
 n 0 1 n
 Chọn x=1 thì: 2 = C n + C n +  + C n 
 Toán Rời Rạc - ĐHSPHN 
 Luyện tập 
31 
 0 2 2n 1 3 2n-1
 8. CM: C 2n+C 2n+..+C 2n=C 2n+C 2n+..+C 2n 
 2n 2n
 2n k k 2n k k k
 x 1 C2n x 1 C2n x
 k 0 k 0
 Với x = -1 thì: 
 0 1 2 3 2n-1 2n
 0 = C 2n - C 2n + C 2n – C 2n+-C 2n+C 2n 
 0 2 2n 1 3 2n-1
 C 2n+C 2n++C 2n = C 2n+C 2n++C 2n 
 Toán Rời Rạc - ĐHSPHN 
 Luyện tập 
32 
 9. Khai triển đa thức: 
 P(x)=(x+1)10 + (x+1)11 + (x+1)12 + (x+1)13 + (x+1)14 
 2 14
 ra dạng: P(x) = a0 + a1x + a2x +  + a14x . 
 tính a10? 
 Toán Rời Rạc - ĐHSPHN 
 Khai triển lũy thừa của đa thức 
33 
  Định lý. Cho m, n là 2 số nguyên dương. Khi 
 đó ta có: 
 n n! kk12 km
 (x1 x 2 ... xmm )  x 1 x 2 ... x
 k12 k ... km n k12! k !... km !
 tổng được lấy trên tất cả các bộ m số tự nhiên 
 (k1,k2,,km) sao cho k1 + k2 ++ km = n. 
 Toán Rời Rạc - ĐHSPHN 
 Ví dụ 
34 
 3 3! k k k
 x x x x 1 x 2 x 3
 1 2 3  k !k !k ! 1 2 3
 k1 k2 k3 3 1 2 3
 Tất cả các bộ (k1,k2,k3) sao cho k1+k2+k3=3 là: 
 (3,0,0), (2,1,0), (2,0,1), (1,2,0), (1,0,2), (1,1,1), 
 (0,3,0), (0,2,1), (0,1,2), (0,0,3). 
 Toán Rời Rạc - ĐHSPHN 
35 Công thức Tổ hợp trong tập hợp 
 Toán Rời Rạc - ĐHSPHN 
 Số phần tử của một hợp các tập hợp 
36 
  Ví dụ: Bài kiểm tra Toán có 2 câu hỏi. Cả lớp 
 có 30 em làm được câu thứ nhất, 20 em làm 
 được câu thứ hai, và chỉ có 10 em làm được 
 cả hai câu. Tìm số học sinh cả lớp? 
  A tập hợp học sinh giải được câu thứ nhất 
  B tập hợp học sinh giải được câu thứ hai 
  A∩B là tập hợp học sinh giải được cả hai câu 
 |A∪B| = |A| + |B| - |A∩B| = 30+20–10 = 40 em 
 Toán Rời Rạc - ĐHSPHN 
 Số phần tử của một hợp các tập hợp 
37 
 |A∪B| = |A| + |B| - |A∩B| 
 |A∪B∪C| = |A|+|B|+|C|-|A∩B|-|B∩C|-|C∩A|+|A∩B∩C| 
 Định lý: cho trước các tập hợp A1,A2,..An. Khi đó: 
 n+1
 |A1∪A2∪ ⋯An|= |Ai|- |Ai∩Bj|++(-1) |A1∩A2∩ ⋯An| 
 Toán Rời Rạc - ĐHSPHN 
 Luyện tập 
38 
 10. Trong một kỳ thi học sinh giỏi Toán, Lý, Hóa. 
 Biết rằng có 20 em thi Toán, 14 em thi Lý, 6 em 
 thi cả Toán và Lý, 5 em thi cả Lý và Hóa, 2 em 
 thi cả Toán và Hóa, và có 1 em tham gia cả 3 
 môn. Hỏi có bao nhiêu em? 
 11. Tính số các mật khẩu tạo được bằng cách 
 hoán vị các chữ cái của từ “TINHOCTRE” sao 
 cho không có hai chữ cái nào giống nhau đứng 
 cạnh nhau? 
 Toán Rời Rạc - ĐHSPHN 
THANK YOU!