Bài giảng Toán rời rạc - Chương 1: Logic mệnh đề - Bùi Thị Thủy
Thế nào là một mệnh đề?
Các toán tử logic?
Và, hoặc, hội, tuyển, kéo theo
Phân tích mệnh đề logic phức hợp
“Bạn không được đi xe máy, nếu bạn dưới 16 tuổi
trừ phi đó là xe phân khối nhỏ hoặc khi bạn có
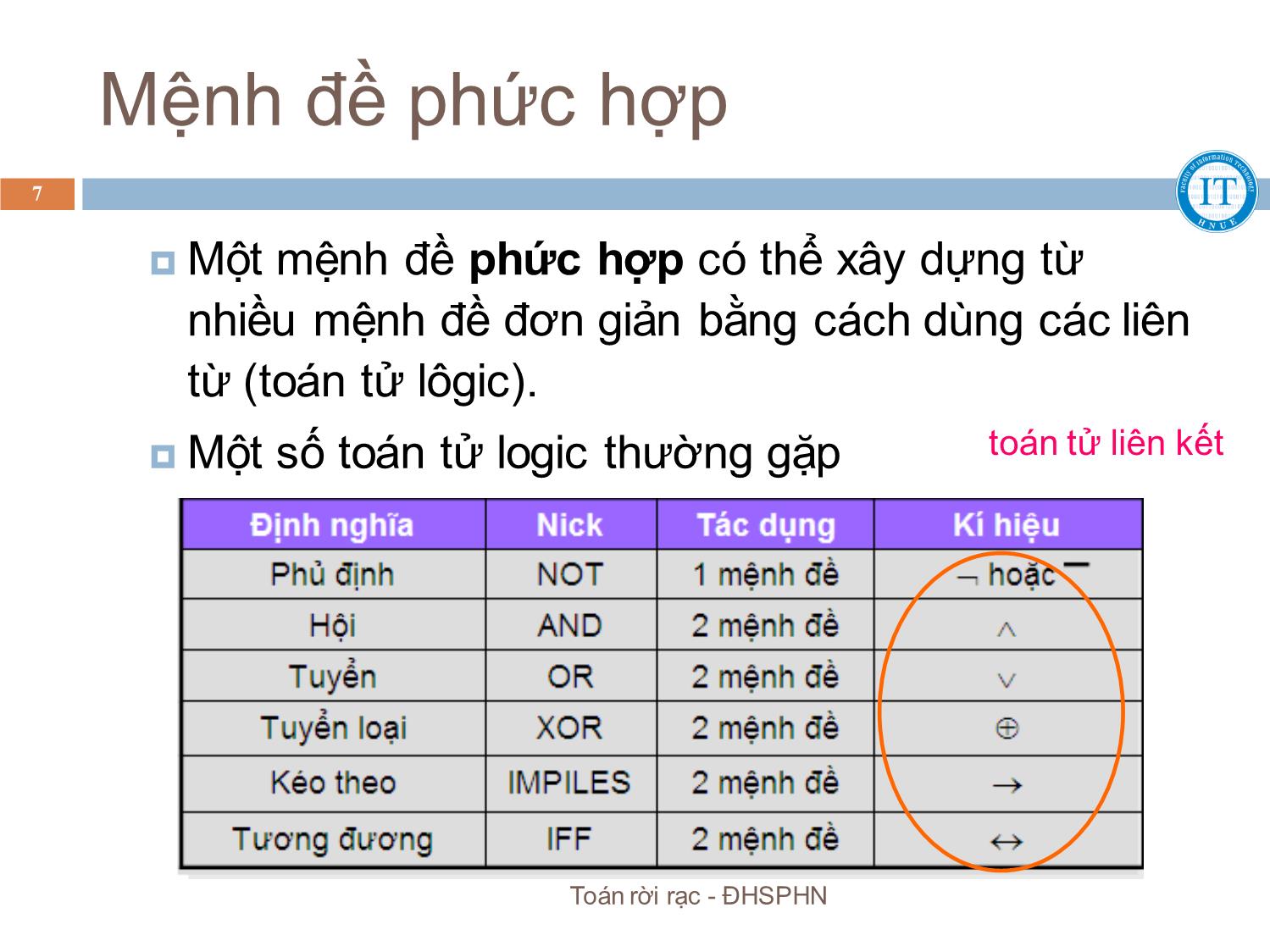
giấy phép đặc biệt.”
Các phép toán logic với các bit?
Bit? Phép toán bit OR, AND, XOR?

Trang 1

Trang 2

Trang 3

Trang 4

Trang 5

Trang 6
Trang 7

Trang 8
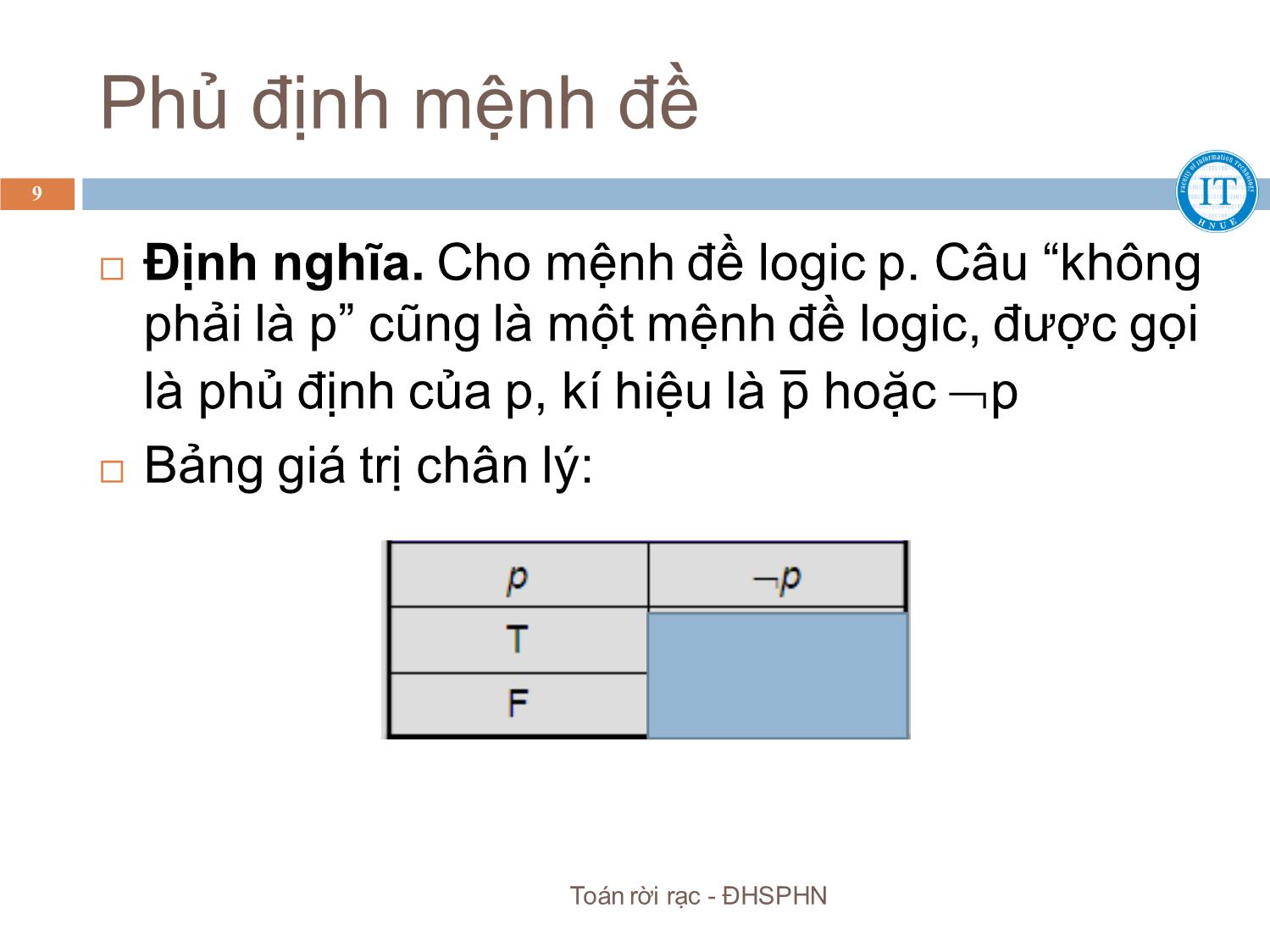
Trang 9
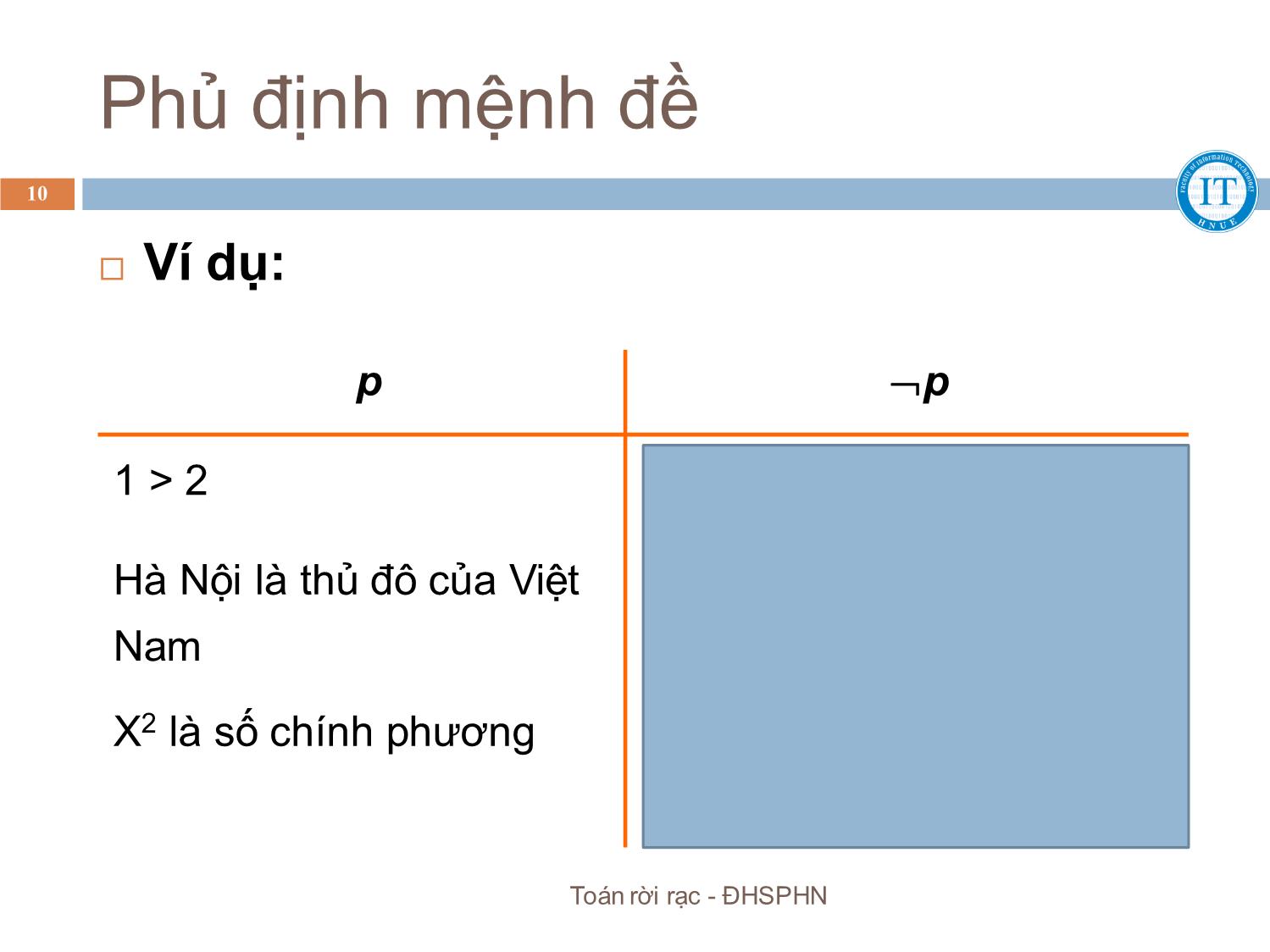
Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Toán rời rạc - Chương 1: Logic mệnh đề - Bùi Thị Thủy", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Toán rời rạc - Chương 1: Logic mệnh đề - Bùi Thị Thủy

TOÁN RỜI RẠC (DISCRETE MATHEMATICS) Bùi Thị Thủy Đặng Xuân Thọ Support 2 TS. Đặng Xuân Thọ Mobile: 091.2629.383 Email: thodx@hnue.edu.vn Website: Toán rời rạc - ĐHSPHN NỘI DUNG 3 Chương 1. Logic mệnh đề Chương 2. Lý thuyết tập hợp Chương 3. Một số công thức tổ hợp Chương 4. Suy luận và kiểm chứng chương trình Chương 5. Đại số Boole và cấu trúc mạch logic Chương 6. Thuật toán Chương 7. Lý thuyết đồ thị Toán rời rạc - ĐHSPHN Chương 1. Logic mệnh đề 4 Thế nào là một mệnh đề? Các toán tử logic? Và, hoặc, hội, tuyển, kéo theo Phân tích mệnh đề logic phức hợp “Bạn không được đi xe máy, nếu bạn dưới 16 tuổi trừ phi đó là xe phân khối nhỏ hoặc khi bạn có giấy phép đặc biệt.” Các phép toán logic với các bit? Bit? Phép toán bit OR, AND, XOR? Toán rời rạc - ĐHSPHN Mệnh đề logic 5 Định nghĩa. Một mệnh đề (logic) (p, q, r, s,) là một khẳng định mà nội dung của nó là đúng hoặc là sai, chứ không thể vừa đúng vừa sai. Ví dụ: Một với một là hai Mệnh đề Hai thêm hai là bốn Mệnh đề Bốn với một là năm Mệnh đề Năm ngón tay sạch đều Không là mệnh đề Toán rời rạc - ĐHSPHN Mệnh đề logic 6 Giá trị chân lý của một mệnh đề Một mệnh đề logic được gán giá trị T (true) nếu nó đúng hoặc F (false) nếu nó sai Các giá trị T, F được gọi là giá trị chân lý của mệnh đề đã cho Bảng giá trị chân lý: p: “Hà Nội là thủ đô của VN” p q q: “Tổng các góc của một T F tam giác bằng 100o” Toán rời rạc - ĐHSPHN Mệnh đề phức hợp 7 Một mệnh đề phức hợp có thể xây dựng từ nhiều mệnh đề đơn giản bằng cách dùng các liên từ (toán tử lôgic). Một số toán tử logic thường gặp toán tử liên kết Toán rời rạc - ĐHSPHN Mệnh đề phức hợp 8 Ví dụ: Nếu x là số nguyên, thì x2 cũng là số nguyên. Trời vừa nắng, vừa mưa. Để được đi du học, hoặc là bạn phải giỏi hoặc là bạn phải có tiền tự túc. Bạn không được đi xe máy nếu bạn dưới 16 tuổi trừ phi đó là xe phân khối nhỏ hoặc khi bạn có giấy phép đặc biệt. Toán rời rạc - ĐHSPHN Phủ định mệnh đề 9 Định nghĩa. Cho mệnh đề logic p. Câu “không phải là p” cũng là một mệnh đề logic, được gọi là phủ định của p, kí hiệu là p hoặc p Bảng giá trị chân lý: Toán rời rạc - ĐHSPHN Phủ định mệnh đề 10 Ví dụ: p p 1 > 2 1 ≤ 2 Hà Nội là thủ đô của Việt Hà Nội không là thủ đô Nam của Việt Nam X2 là số chính phương X2 không là số chính phương Toán rời rạc - ĐHSPHN 11 Các toán tử logic Toán rời rạc - ĐHSPHN Phép hội 12 Định nghĩa. Cho trước hai mệnh đề logic p, q. Câu nói “p và q” cũng là một mệnh đề logic, được gọi là hội của p và q, kí hiệu p q. p q chỉ đúng khi cả p và q đều đúng và sai trong các trường hợp còn lại. Toán rời rạc - ĐHSPHN Phép hội 13 Ví dụ: p: “Bác Hồ sinh ngày 19/5”; q: “Bác Hồ quê ở Nghệ An”. p q: “Bác Hồ sinh ngày 19/5 và Bác Hồ quê ở Nghệ An”. p q: “Bác Hồ sinh ngày 19/5 và Bác Hồ quê không ở Nghệ An”. p q: “Bác Hồ không sinh ngày 19/5 và Bác Hồ quê ở Nghệ An”. Toán rời rạc - ĐHSPHN Phép tuyển 14 Định nghĩa. Cho trước hai mệnh đề logic p, q. Câu nói “p hoặc q” cũng là một mệnh đề logic, được gọi là tuyển của p và q, Kí hiệu: p q. p q chỉ sai khi cả p và q đều sai và đúng trong các trường hợp còn lại. Toán rời rạc - ĐHSPHN Phép tuyển 15 Ví dụ: p: “Hồ Xuân Hương sinh ngày 3/5”; q: “Hồ Xuân Hương sinh ngày 9/5”; thì p v q là: “Hồ Xuân Hương sinh ngày 3/5 hoặc vào ngày 9/5”; Toán rời rạc - ĐHSPHN Phép tuyển có loại 16 Định nghĩa. Cho trước hai mệnh đề logic p, q. Câu nói “hoặc p hoặc q” cũng là một mệnh đề logic, được gọi là tuyển có loại của p và q, Kí hiệu: p q. p q đúng khi một trong hai p hoặc q đúng và sai trong trường hợp còn lại. Toán rời rạc - ĐHSPHN Phép tuyển có loại 17 Ví dụ: p: “Hồ Xuân Hương sinh ngày 3/5”; q: “Hồ Xuân Hương sinh ngày 9/5”; thì p q là: “Hồ Xuân Hương hoặc sinh ngày 3/5 hoặc vào ngày 9/5”; Có nghĩa rõ ràng là Hồ Xuân Hương chỉ có thể sinh vào một trong hai ngày 3/5 hoặc 9/5. Toán rời rạc - ĐHSPHN Phép kéo theo 18 Định nghĩa. Cho trước hai mệnh đề logic p, q. Câu nói “nếu có p thì có q” cũng là một mệnh đề logic, được gọi là phép kéo theo của p và q, kí hiệu p q. p q chỉ sai nếu p đúng, q sai và đúng trong các trường hợp còn lại. Toán rời rạc - ĐHSPHN Phép kéo theo 19 Ví dụ: p: “Tam giác ABC vuông tại đỉnh A”; q: “BC2 = CA2 + AB2” p q: “Tam giác ABC vuông tại đỉnh A thì BC2 = CA2 + AB2” Toán rời rạc - ĐHSPHN Phép tương đương 20 Định nghĩa. Cho trước hai mệnh đề logic p, q. Câu nói “p tương đương với q” cũng là một mệnh đề logic, kí hiệu p q. Mệnh đề p q chỉ đúng khi p và q cùng đúng hoặc cùng sai. Toán rời rạc - ĐHSPHN Phép tương đương 21 Ví dụ: p: “Tam giác ABC là tam giác đều”; q: “Tam giác ABC có 3 cạnh bằng nhau” p q: “Tam giác ABC đều khi và chỉ khi tam giác ABC có ba cạnh bằng nhau”. Toán rời rạc - ĐHSPHN Thứ tự ưu tiên 22 Quy tắc: Trong một mệnh đề phức hợp gồm nhiều toán tử lôgic, để chỉ định thứ tự thực hiện các toán tử lôgic ta dùng các dấu ngoặc. Khi không có dấu ngoặc thì thứ tự ưu tiên được thể hiện như sau: → thứ tự ưu tiên Toán rời rạc - ĐHSPHN Dịch câu 23 Xác định các toán tử logic (các liên từ) Xác định các mệnh đề thành phần Ví dụ: “Bạn không được đi xe máy nếu bạn dưới 16 tuổi trừ phi đó là xe phân khối nhỏ hoặc khi bạn có giấy phép đặc biệt” Các mệnh đề: Bạn được đi xe máy (p) Xe máy có phân khối nhỏ (r) Bạn dưới 16 tuổi (q) Bạn có giấy phép đặc biệt (s) (q (r s)) p Toán rời rạc - ĐHSPHN 24 Biểu thức logic & sự bằng nhau Toán rời rạc - ĐHSPHN Biểu thức logic 25 Định nghĩa. Một biểu thức logic là một biểu thức được tạo thành từ các biến logic cho trước bằng cách áp dụng các toán tử logic và dấu ngoặc “(”, “)” một cách hình thức. Ví dụ: ((p q) r) p (q (r s)) p Toán rời rạc - ĐHSPHN Tương đương logic 26 Định nghĩa. Một biểu thức logic luôn có giá trị chân lý T (F) với bất cứ giá trị chân lý nào của các mệnh đề thành phần được gọi là hằng đúng T (hằng sai F). Biểu thức logic không phải hằng đúng hoặc hằng sai gọi là tiếp liên. Hằng đúng Hằng sai Tương đương logic 27 Định nghĩa. Các mệnh đề logic p và q được gọi là tương đương logic nếu biểu thức logic pq là mệnh đề logic hằng đúng. Khi đó p, q gọi là 2 mệnh đề logic tương đương (bằng nhau), kí hiệu p q. Giống nhau Tương đương logic 28 Tính chất: Phản xạ: với p, ta luôn có p p Đối xứng: Nếu p q thì q p Bắc cầu: Nếu p q, q r thì p r Khử kéo theo: (p q) (p q) (chứng minh) Ví dụ: CMR (p q) (p q) là hằng đúng? Toán rời rạc - ĐHSPHN Các đẳng thức cơ bản 29 Cho p, q, r là các mệnh đề Tương đương logic 30 Ví dụ: Cho mệnh đề p,q. Chứng minh: (p(pq)) pq Sử dụng các tương đương logic cơ bản, ta có: (p (p q ) p (p q ) (De Morgan) p [(p) q ] (De Morgan) p [p q ] (phủ định kép) (p p) (p q) (phân phối) F (p q) (phủ định) (p q) F (giao hoán) p q (đồng nhất) 31 Các phép toán logic với các bit Toán rời rạc - ĐHSPHN Phép toán bit OR, AND, XOR, NOT 32 Một bit có hai trạng thái thường kí hiệu là 0, 1 Bit dùng để biểu diễn các giá trị chân lý: 0 tương ứng F 1 tương ứng T Biến Boole: có giá trị là 1 (T) hoặc 0 (F) Các toán tử , , , tương ứng với các phép toán OR, AND, XOR, NOT Toán rời rạc - ĐHSPHN Phép toán bit OR, AND, XOR, NOT 33 Bảng tính OR AND XOR 0 1 0 1 0 1 0 0 1 0 0 0 0 0 1 1 1 1 1 0 1 1 1 0 Toán rời rạc - ĐHSPHN Phép toán bit OR, AND, XOR, NOT 34 Định nghĩa. Một xâu bit là một dãy gồm không hoặc nhiều bit. Độ dài xâu bit là số các bit trong xâu đó. Các phép toán OR – bit, AND – bit, XOR – bit thực hiện trên 2 xâu bit có cùng độ dài: thực hiện các phép toán OR, AND, XOR tại các bit tương ứng trong 2 xâu. Toán rời rạc - ĐHSPHN Phép toán bit OR, AND, XOR, NOT 35 Ví dụ: 1001 0111 = 1111 1001 0111 = 0001 1001 0111 = 1110 Toán rời rạc - ĐHSPHN THANK YOU!
File đính kèm:
 bai_giang_toan_roi_rac_chuong_1_logic_menh_de_bui_thi_thuy.pdf
bai_giang_toan_roi_rac_chuong_1_logic_menh_de_bui_thi_thuy.pdf

