Bài giảng Tập mờ-thô và ứng dụng trong khai phá dữ liệu - Hà Quang Thụy

u6, u7, u8, u5} RX2 = {u1, u4, u5, u8, u7, u6} 9
Không gian xấp xỉ
 ⚫ Khái niệm
 ▪ Cho với U: tập đối tượng, R: quan hệ tương đương trên U
 ▪ XU: cặp tập xấp xỉ X, “tập thô”
 ▪ được gọi là không gian xấp xỉ.
 ▪ Độ chính xác R(X)=|RX|/|RX|=card(RX)/card(RX)
 ⚫ Tính chất tập xấp xỉ
 ▪ RX  X  RX
 ▪ R()= = R() RU= U= RU
 ▪ X  Y RX  RY và RX  RY
 ▪ R(XY)= RXRY R(XY)=RXRY
 ▪ R(XY)  RXRY R(XY)RXRY
 ▪ R(U\X) = U\ RX R(-X) = - RX
 ▪ R(RX)= R(RX)=RX R(RX)=R(RX)=RX
 ⚫ Bốn “kiểu” tập thô (không xét R(X)=1: X rõ)
 ▪ RX  và RX U “thô” xác định 0< R(X)<1
 ▪ RX= và RX U “thô” không xác định dưới R(X)=0
 ▪ RX  và RX =U “thô” không xác định trên 0< R(X)<1
 ▪ RX= và RX =U “thô” không xác định hoàn toàn (X)=0
 R 10
Xấp xỉ theo quan hệ hai ngôi bất kỳ
 ⚫ Khái niệm
 ▪ Cho với U: tập đối tượng, R: quan hệ hai ngôi trên U
 ▪ “rừng” Ru (Ru-forests): u U: Ru = {v| v U và (v,u) R}
 ▪ R tương đương u1, u2 U: Ru1Ru2 | Ru1Ru2=
 ▪ R tương đương: U=U1+U2++Uk “phân hoạch” U
 ▪ R không tương đương: U=(u U)Uy “phủ” U
 ⚫ Tập xấp xỉ dưới (ba khả năng)
 ▪ Cho X  U
 ▪ u U: u thuộc RX khi-chỉ khi (chọn một khả năng định nghĩa)
 ▪ Mọi rừng chứa u đều nằm trong X
 ▪ Ít nhất một rừng chứa u nằm trong X
 ▪ Rừng Ru nằm trong X
 ⚫ Tập xấp xỉ trên (ba khả năng)
 ▪ Cho X  U. u U: u thuộc RX khi-chỉ khi
 ▪ Mọi rừng chứa u có giao khác rỗng với X
 ▪ Ít nhất một rừng chứa u có giao khác rỗng với X
 ▪ Rừng Ru có giao khác rỗng với X
 [Cornelis08] Chris Cornelis, Martine De Cock, Anna Maria Radzikowska. Fuzzy
 Rough Sets: from Theory into Practice. Handbook of Granular 11
 Computing, 2008
Định nghĩa hình thức
 ⚫ Cho trước
 ▪ Cho với U: tập đối tượng, R: quan hệ hai ngôi trên U
 ▪ Cho X  U
 ⚫ Tập xấp xỉ dưới chặt, lỏng, thường
 ▪ Chặt: u U: u RX (v U: u Rv → Rv  X}
 ▪ Lỏng: u U: u RX (v U: u Rv  Rv  X}
 ▪ Thường: u U: u RX Ru  X
 ⚫ Tập xấp xỉ trên chặt, lỏng, thường
 ▪ Chặt: u U: u RX (v U: u Rv → RvX }
 ▪ Lỏng: u U: u RX (v U: u Rv  RvX }
 ▪ Thường: u U: u RX Ru  X 
 ⚫ Ví dụ
 ▪ Cho như bảng bên, X={x1,x3}
 ▪ RX = {x3} RX = {x1,x2, x3}
 ▪ RX = {x1,x3} RX = {x1,x3}
 ▪ RX =  RX = U
 12
Bảng quyết định
⚫ Khái niệm
 ▪ Bảng quyết định: Hệ thông tin đặc biệt
 ▪ DT=, ConDec=. Thuộc tính điều kiện Con và
 thuộc tính quyết định Dec. Ví dụ, thuộc tính Walk hoặc Flu.
 ▪ Tập thuộc tính quyết định Dec có thể có nhiều thuộc tính quyết định
 ▪ Quan hệ Con → Dec Luật phân lớp ?
 13
Miền dương của tập thuộc tính
 ⚫ Miền dương của tập thuộc tính điều kiện
 ▪ Cho bảng quyết định DT=
 ▪ BC: vùng B dương của D: PosB(D):hợp mọi tập sơ cấp theo
 quan hệ B nằm trong tập sơ cấp quan hệ D. PosB(D)=
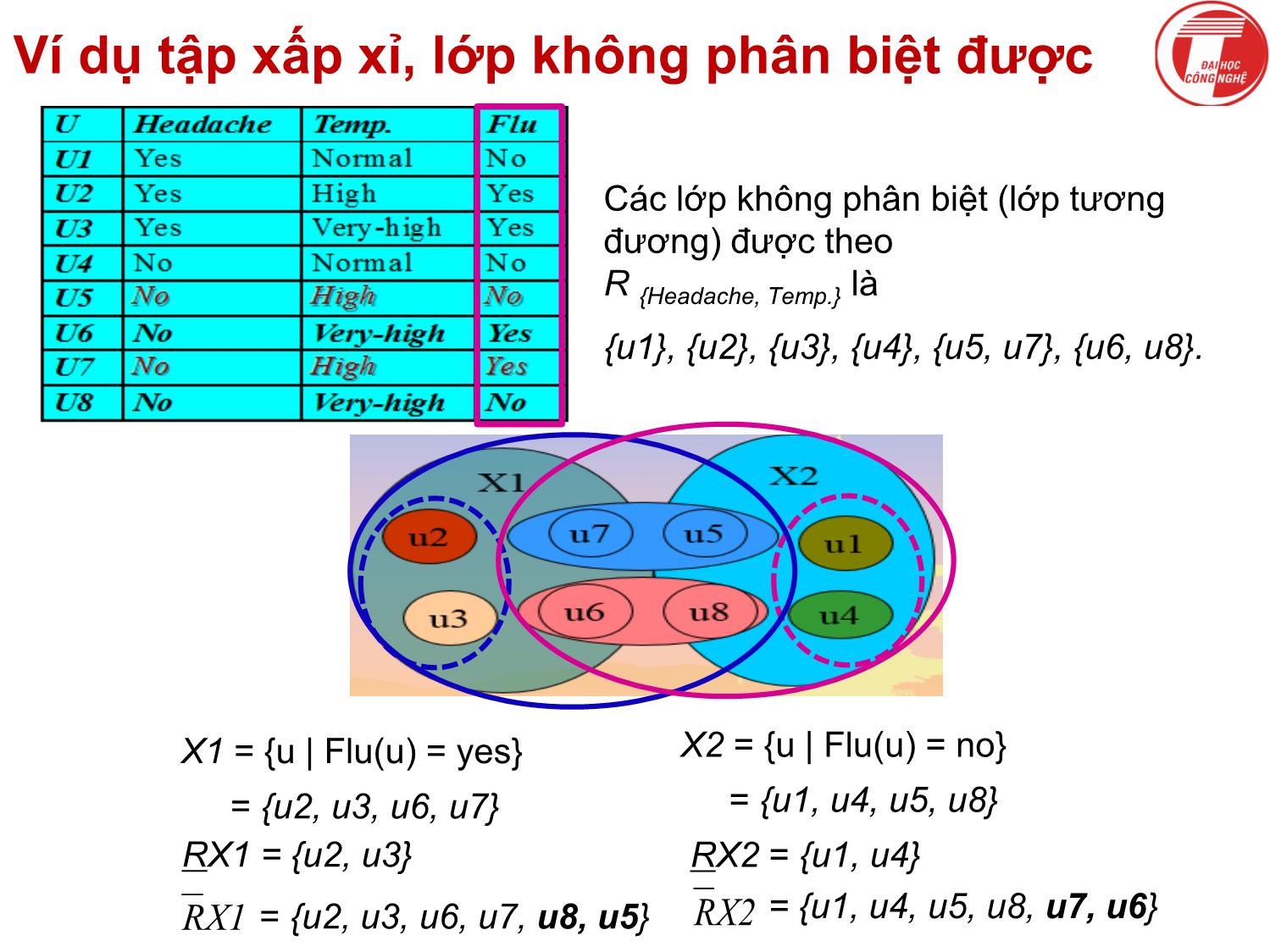
 ▪ Ví dụ, D=Flu có hai tập sơ cấp {u1,u4,u5,u8}, {u2,u3, u6, u7}
 ▪ B={Headache, Temp.} có các tập sơ cấp {u1}, {u2}, {u3}, {u4},
 {u5,u7}, {u6,u8} như vậy PosB(D) = {u1,u2,u3,u4}.
 ▪ PosHeadache(D)=; PosTemp.(D)=
 14
Hệ thông tin đa trị
 ⚫ Định nghĩa
 ▪ S=; U, A, V có ý nghĩa như trong hệ thông tin “đơn
 trị” ngoại trừ hàm thông tin: :U A →2V.
 ▪ Chủ đề thời sự
 ⚫ Ví dụ
 ▪ Ví dụ, Anh (E), Pháp (F), Trung Quốc (H), Nga (R), Nhật Bản
 (J), Hàn quốc (K), v.v.}
 ▪ Thuộc tính kỹ năng ngoại ngữ (nghe R, nói S, đọc R, viết W).
 Mỗi kỹ năng liên quan tới một số ngoại ngữ.
 15
Quan hệ dung sai trong hệ thông tin đa trị
 ⚫ Định nghĩa
 ▪ Hệ thông tin đa trị S=<U, A, V, }
 ▪ B A: định nghĩa quan hệ dung sai/thứ lỗi TB:
 TuB =  vUUbB ( ,,)  b ub  v ( ) ( ) 
 ▪ TB đáp ứng tính phản xạ, tính giao hoán (đối xứng)
 ▪ Lớp dung sai TB(u) = {v U: (u,v) TB}
 ⚫ Một vài tính chất
 ▪ Ký hiệu U/TB = {TB(u)| u U} tập các lớp dung sai do TB. Khi
 đó, U/TB tạo nên một “phủ” của U.
 ▪  BC A → TC  TB .
 ⚫ Tập xấp xỉ theo quan hệ dung sai
 ▪ Tương tự xây dựng TB, TB
 16
Ứng dụng tập thô trong khai phá dữ liệu
 ⚫ Giới thiệu
 ▪ Nhiều ứng dụng của tập thô trong khai phá dữ liệu
 ▪ Hai ứng dụng điển hình là tìm kiếm rút gọn (reducts, lựa chọn)
 thuộc tính và tìm kiếm các luật quyết định (decision rules)
 ⚫ Một số ký hiệu
 ▪ Cho hệ thông tin S=(U, RA) với A là tập thuộc tính
 ▪ Gọi P(A) là tập tất cả các tập con của A
 +
 ▪ Ứng với S, xây dựng hàm đánh giá S: P(A) →R đáp ứng hai
 điều kiện:
 ❖ (i) BA: S(B) được tính dựa vào hàm thông tin trên tập
 B là INF(B)
 ❖ (ii) S là một hàm đơn điệu: B CA: S(B) S(C)
 17
Không gian xấp xỉ mờ
 ⚫ Khái niệm
 ▪ U: tập đối tượng khác rỗng
 ▪ R: QH tương đương không gian xấp xỉ
 ▪ X(u) = 1 (v U) (R(u,v) = 1→X(v) = 1)
 ▪ X(u) = 1 (v U) (R(u,v) = 1  X(v) = 1)
 ▪ R: QH tương tự không gian xấp xỉ mờ
 18
2. Tập mờ
 ⚫ Ý nghĩa của tập mờ
 ▪ Biểu diễn một tính chất của các đối tượng mà nhận thức về tính
 chất đó ở mỗi đối tượng là “mờ” (không rõ ràng). Con người
 có đánh giá khác nhau về tính chất đó trong mỗi đối tượng
 ▪ Tính chất “trẻ”-”già”, “xinh”, ”đẹp” v.v. của một người
 ▪ “Tập mờ” thực chất không là một tập “thông thường”
 ⚫ Định nghĩa tập mờ
 ▪ Cho U={đối tượng} . XU : hàm đặc trưng X: U→{0,1}
 ▪ Tập mờ (fuzzy set) X với X: U→[0,1], X cũng “hàm mờ”
 ▪ Nhắt cắt  ( [0,1]) của tập mờ X= {u U: X(u) } là một tập rõ
 ▪ “Lực lượng” tập mờ X (X): |X|=card (X) = u UX(u)
 ▪ X, Y là hai tập mờ: XY u U: X(u) X(u)
 ▪ X tập mờ: tập bù của X (X), u U: X(u)= 1 - X(u)
 ⚫ Xuất xứ
 ▪ A. Zadeh, 1965.
 ▪ https://www2.eecs.berkeley.edu/Faculty/Homepages/zadeh.html
 1921- 19
Toán tử trên tập mờ
 ⚫ Phép toán logic liên quan tập mờ
 ▪ XY, XY? : tương ứng toán tử logic giao , hợp . Kéo theo →
 ▪ Chuẩn t (triangular “tam giác”, t-norm) T, cộng chuẩn t (t-conorm)
 S: [0,1] [0,1]→[0,1]
 ❖ T và S tăng theo hai đối số: u,v,u1,v1 [0,1], u u1,
 v v1→T(u,v) T(u1,v1), S(u,v) S(u1,v1).
 ❖ T và S giao hoán (commutative): T(u,v)= T(v,u), S(u,v)= S(v,u)
 ❖ T và S kết hợp (associative): T(u1+u2,v)= T(u1,v)+T(u2,v),
 T(u,v1+v2)= T(u,v1)+T(u,v2). Tương tự với S
 ❖ T/S thỏa điều kiện biên “1”/“0”: u [0,1]: T(u,1)=S(u,0)=u
 ▪ Nghịch đảo (negator) I: [0,1]→[0,1]: giảm, N(1)=0, N(0)=1, 1-x
 ▪ Kéo theo I: [0,1] [0,1]→[0,1]:
 ❖ I giảm theo đối số thứ nhất và tăng theo đối số thứ hai
 ❖ I thỏa các điều kiện biên: I(1,0)=0, I(1,1)=I(1,0)=I(0,0)=1
 20
Toán tử trên tập mờ
 ⚫ Một số chuẩn điển hình
 ▪ Chuẩn-t: min (u,v), tích u*v, chuẩn t Lukasewic max (0, u+v-1).
 min (u,v) là chuẩn t lớn nhất. Định nghĩa giao của hai tập mờ
 ▪ Cộng chuẩn-t: max (u,v), tổng xác xuất u+v-u*v, cộng chuẩn t
 Lukasewic min (1, u+v). max (u,v) là cộng chuẩn-t nhỏ nhất. Định
 nghĩa hợp của hai tập mờ
 ▪ Kéo theo Lukasewic: min (1, 1-x+y)
 21
Quan hệ dung sai (thứ lỗi)
 ⚫ Quan hệ mờ
 ▪ U, V hai tập bất kỳ
 ▪ Quan hệ mờ của U và V là hàm mờ trên U V : U V→[0,1]
 ▪ Quan hệ mờ hai ngôi trên U là hàm mờ trên U U : U U→[0,1]
 ⚫ Quan hệ dung sai và quan hệ tương tự
 ▪ Quan hệ dung sai (tolerance relation)
 ❖ Quan hệ mờ hai ngôi trên U
 ❖ Phản xạ (reflexive): u U: R(u,u)= 1
 ❖ Đối xứng (symmetric): u, v U: R(u,v)= R(v,u)
 ▪ Quan hệ tương tự (similary relation):
 ❖ R là quan hệ dung sai: phản xạ, đối xứng và
 Bắc cầu sup-min: R(u,v) supx Umin (R(u,x), R(x,v))
 ❖ u U: tập mờ “lớp tương tự mờ” [u]R: y U thì [u]R(y)=R(u,y)
 ❖ Cho R: QH tương tư,̣ T: t-chuẩn trên U 
 R(u,v) = supx UT(R(u,x), R(x,v))
 ▪ Ví dụ: xác định quan hệ tương tự giữa các vector, các văn bản 
 ▪ Quan hệ tương tự nền tảng cho Phân cụm, Phân lớp k-NN và
 nhiều bài toán liên quan khác
 22
Tập mờ: nghiên cứu và một vài chủ đề
 ⚫  :
 ▪ 39000+ bài báo ~ "fuzzy set"
 ▪ 16240+ bài báo ~ "fuzzy system"
 ▪ 1190+ bài báo ~ "fuzzy classifier“
 ▪ 6100+ bài báo ~ "fuzzy classifier“
 ▪ 940+ bài báo ~ "fuzzy pattern“
 ▪ 290+ bài báo ~ "fuzzy association rule"
 ⚫ Biến ngôn ngữ
 ▪ Biến ngôn ngữ: linguistic variable
 ▪ “Biến”: giá trị là các từ/câu trong ngôn ngữ tự nhiên hoặc nhân tạo
 ▪ Bộ năm (X, T(X), U, G, M). X là tên biến “tuổi”,
 ▪ T(X) là tập “term - số hạng” giá trị ngôn ngữ “trẻ”, “già”, “trung
 niên”, “măng tơ” ,
 ▪ U là tập diễn ngôn,
 ▪ G là tập quy tắc cú pháp sinh ra các giá trị ngôn ngữ
 ▪ M: tập quy tắc ngữ nghĩa: mỗi giá trị ngôn ngữ → ngữ nghĩa M(X)
 là tập mờ của U, “khả năng tương thích”
 ▪ Đại số gia tử: Trường hợp riêng của biến ngôn ngữ và tính toán từ
 Zadeh.The Concept of a Linguistic Variable and its Applications. Approximate 23
 Reasonin I,II, III. 1975
Tính toán từ và tập mờ cấp k
 ⚫ Tính toán từ và
 ▪ Tính toán từ (computing with word: CWW): Sử dụng từ: (i) là cần
 thiết (không biết số lượng ), (ii) Là có ích (số đã biết, thứ lỗi do
 thiếu chính xác, lời nói là đủ tốt), (iii) Tiện lợi (Tổng hợp bằng từ)
 ⚫ Tập mờ cấp k
 ▪ Biến ngôn ngữ: linguistic variable. Bộ năm (X, T, U, G, M) với X là
 tên biến “tuổi”, T là tập giá trị ngôn ngữ “trẻ”, “già”, “trung niên”,
 “măng tơ” , U là tập diễn ngôn, G là tập quy tắc cú pháp, M là
 tập quy tắc ngữ nghĩa
 ▪ Tập mờ cấp k. Tập mờ cấp 2 (2-type fuzzy set): U tập nền, F={tập
 mờ cấp 1 trên U}, X tập mờ trên F được gọi là tập mờ kiểu 2 trên
 U. U ~ Fo, F ~ F1. Fk+1 là tập mờ trên Fk.
 24
Tập mờ: ứng dụng
 ⚫ Giới thiệu chung
 ▪ Biểu diễn và lập luận tri thức
 ▪ Miền ứng dụng điển hình: Hệ chuyên gia, Hệ thống điều khiển, hệ
 thống y tế 
 ⚫ Hệ thống mờ: Ứng dụng điển hình
 ▪ Rất nhiều trong công nghiệp: Người máy, Máy giặt,
 ▪ Luật IF-THEN và suy luận mờ: từ chuyên gia / công cụ hỗ trợ
 ▪ Mờ hóa và giải mờ
 25
Luật mờ trong tài chính
 ◼ Trend Rule
 IF DAX = decreasing AND US-$ = decreasing
 THEN DAX prediction = decrease
 WITH high certainty
 ◼ Turning Point Rule
 IF DAX = decreasing AND US-$ = increasing
 THEN DAX prediction = increase
 WITH low certainty
 ◼ Delay Rule
 IF DAX = stable AND US-$ = decreasing
 THEN DAX prediction = decrease
 WITH very high certainty
 ◼ In general
 IF x1 is m1 AND x2 is m2
 THEN y = h
 WITH weight k 
 Prof. Dr. Rudolf Kruse. Fuzzy Systems. Otto-von-Guericke University of Magdeburg. 
 DAX: German stock index. 26
Thuật toán phân cụm mờ FCM
 ⚫ Mô tả
 n
 ▪ Y={y1, y2, , yN}  R : tập dữ liệu
 ▪ c: số lượng cụm trong Y, 2 c<n.
 ▪ m: trọng số mũ. 1 m<
 ▪ U: một ma trận c n phân cụm mờ Y; U Mfc={Uc n|uik [0,1]}
 ▪ V=(v1, v2, vc): vector các trọng tâm (đại diện)
 ▪ vi= (vi1, vi2, , vin) trọng tâm của cụm thứ I
 n
 ▪ A: ma trận xác định dương n n, cảm sinh chuẩn ||.||A trên R :
 ⚫ Thuật toán FCM (fuzzy c-means)
 ▪ Nội dung (LMAX: nguyên, >0;  >0 đủ nhỏ; lỗi )
 (o) (o)
 1) Cố định c, m, A, ||.||A. Chọn một ma trận U = {uij } c n khởi đầu.
 Chạy thuật toán các bước 0, 1, , LMAX
 (k) m (k) m
 2) Tính toán hàm mờ trọng tâm vi=j=1,N(uij ) yj/j=1,N(uij ) , i=1,c
 (k+1) 2/(m-1) -1
 3) Tính toán lại ma trận: uil = (j=1,c (dil/djl) ) , 1 i c, 1 l N
 (k+1) (k)
 4) Kiểm tra hội tụ (so sánh ma trận chuẩn A): Nếu ||U - U ||A  thì
 dừng; ngược lại, U(k) U(k+1) và quay lại (2)
 ▪ U ma trận c n kết quả chính là phân cụm mờ Y cần tìm
 27
Một số vấn đề liên quan FCM
 ⚫ Câu hỏi
 ▪ Ý nghĩa của m và A ?
 ▪ Xác định giá trị của m và A ?
 ⚫ Ý nghĩa của m và A
 ▪ Biến m điều khiển bình phương lỗi, m→1 khó khan trong giảm thiểu
 lỗi, tăng m →  lại làm suy thoái độ mờ của phân cụm.
 ▪ A điều khiển hình dạng cụm “tối ưu giả định” trong y.
 ⚫ Xác đinh giá trị m
 ▪ Không có phương pháp chọn m tối ưu
 ▪ Kinh nghiệm [1.5, 3.0] cho kết quả tốt
 ⚫ Xác đinh giá trị A
 ▪ Ba chuẩn phổ biến nhất
 ▪ Với cy, Cy được xác định theo công thức
 ▪ Đặt ai là các giá trị riêng của Cy. Dy là ma trận đườn chéo {dii=ai}
 ▪ Chuẩn Ơ-cơ-lit: A=I ma trận đơn vị
 -1
 ▪ Chuẩn đường chéo: A= (Dy) .
 -1
 ▪ Chuẩn Mahalanobis: A= (Cy) .
 28
Tập mờ trong khai phá luật kết hợp
 ⚫ Mở hóa giá trị định lượng
 ▪ Khai phá luật kết hợp giao dịch, giá trị
 mục {0,1}
 ▪ Mục giá trị định lượng: giá trị thực
 ▪ Giải pháp rời rạc hóa
 ❖ Tăng số mục
 ❖ phình CSDL
 ❖ Hiện tượng gãy tại các biên rời rạc
 ▪ Khắc phục ba hạn chế này: khai phá
 luật kết hợp mờ
 ⚫ Mờ hóa giá trị định lượng
 ▪ CSDL định lượng D  U A, U tập đối
 tượng, A tập thuộc tính.
 ▪ Mọi loại giá trị định lượng ba giá trị
 mờ là “thấp”, “trung bình”, “cao”. Mỗi
 thuộc tính “mờ” ngưỡng cho từng
 thuộc tính → giá trị {0,1}
 ▪ Mờ hóa toàn cục (hình vẽ); mờ hóa
 cục bộ: mờ hóa cho từng thuộc tính 29
Khai phá luật kết hợp mờ
 ⚫ Một số nghiên cứu gần đây
 ▪ Tzung-Pei Hong và cộng sự
 ▪ Xem danh sách phía dưới
 Tzung-Pei Hong, Guo-Cheng Lan, Yi-Hsin Lin, and Shing-Tai Pan. An Effective Gradual
 Data-ReductionStrategy for Fuzzy Itemset Mining. International Journal of Fuzzy
 Systems, Vol. 15, No. 2, June 2013.
 Chun-Hao Chen, Guo-Cheng Lan, Tzung-Pei Hong, Shih-Bin Lin. Mining fuzzy temporal
 association rules by item lifespans. Appl. Soft Comput. 41: 265-274 (2016)
 Jerry Chun-Wei Lin, Xianbiao Lv, Philippe Fournier-Viger, Tsu-Yang Wu, Tzung-Pei Hong.
 Efficient Mining of Fuzzy Frequent Itemsets with Type-2 Membership Functions.
 ACIIDS (2) 2016: 191-200
 30
3. Tập mờ-thô
 ⚫ Giới thiệu
 ▪ Một tập X, một QH tương đương R, một phép toán “thuộc” Tập thô:
 cặp tập xấp xỉ trên-dưới
 ▪ Một tập mờ X, một QH hai ngôi mờ R, phép toán kéo theo mờ Tập
 mờ-thô: cặp tập xấp xỉ mờ trên-dưới
 ⚫ Một cách xây dựng tập mờ -thô
 ▪ Theo tiếp cận trên và cách chọn các phép toán giao và kéo theo
 ▪ RX:u RX [u]X y U:(y,u) R→y X y U:→((y,u) R, y X)
 ▪ Q/mờ R, tập mờ X, kéo theo mờ T: u RX y U: T(R(y,u), X(y))
 Anna Maria Radzikowska, Etienne E. Kerre. A comparative study of fuzzy 
 rough sets. Fuzzy Sets and Systems 126(2): 137-155 (2002)
 31
Ứng dụng tập mờ-thô trong học máy
 Sarah Vluymans, Lynn D'eer, Yvan Saeys, Chris Cornelis. Applications of Fuzzy
 Rough Set Theory in Machine Learning: a Survey. Fundam. Inform. 142(1-4): 53-3286
 (2015)