Bài giảng Phương pháp tính - Chương 4: Phương pháp tiếp tuyến giải phương trình f(x)=0 - Hà Thị Ngọc Yến
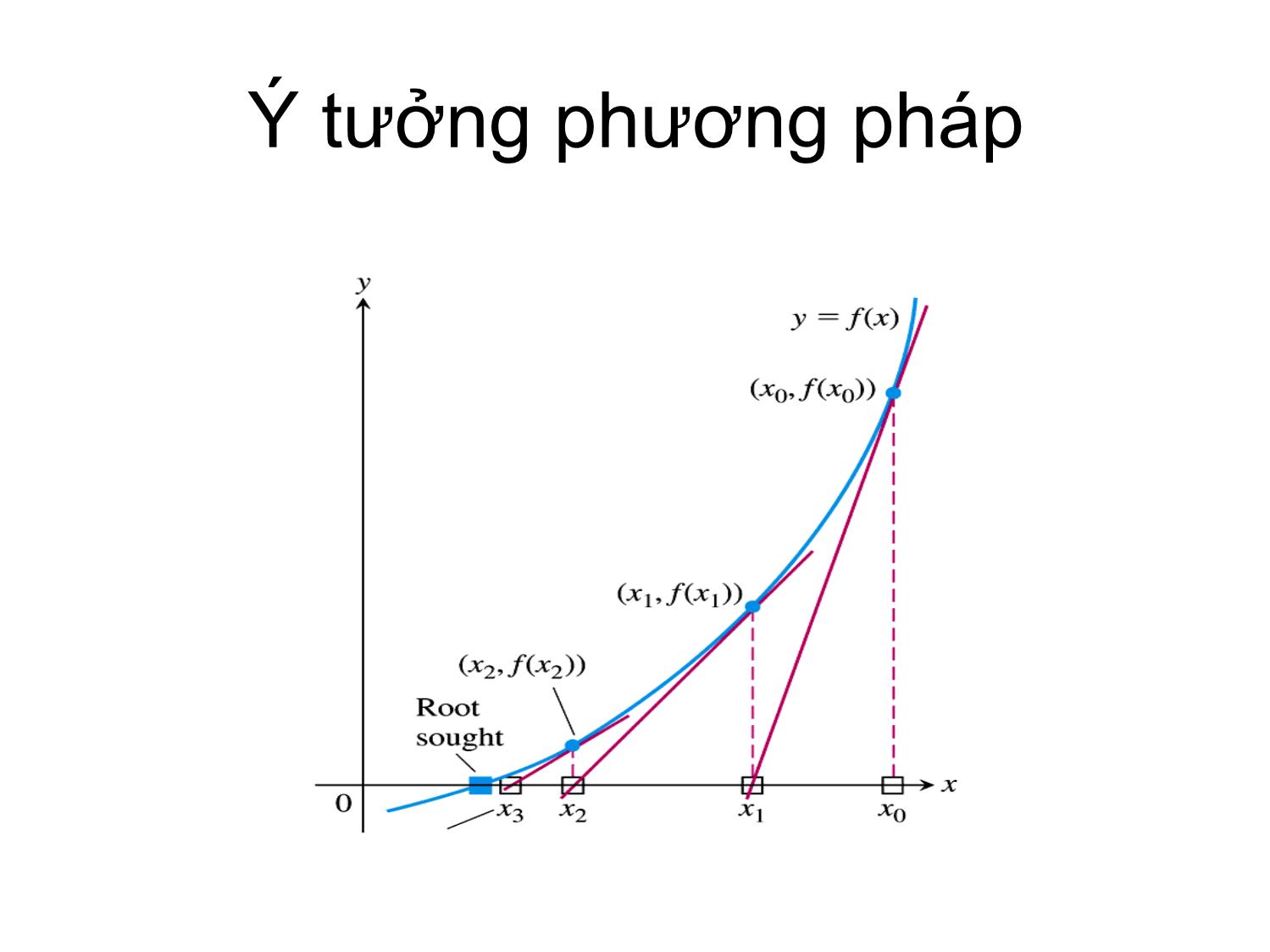
Ý tưởng phương pháp
• Thay thế đường cong trên
[a,b] bằng TIẾP TUYẾN
• Tìm giao điểm của dây cung với trục
hoành thay cho giao điểm đường cong với
trục hoành
y f x Xây dựng công thức
Xét phương trình và k.c.l nghiệm (a,b).
Gọi là điểm Fourie nếu
Chọn điểm Fourie là điểm ban đầu, tức là
Chọn và đặt
Gọi là tiếp tuyến với đồ thị hàm số tại

Trang 1
Trang 2

Trang 3

Trang 4
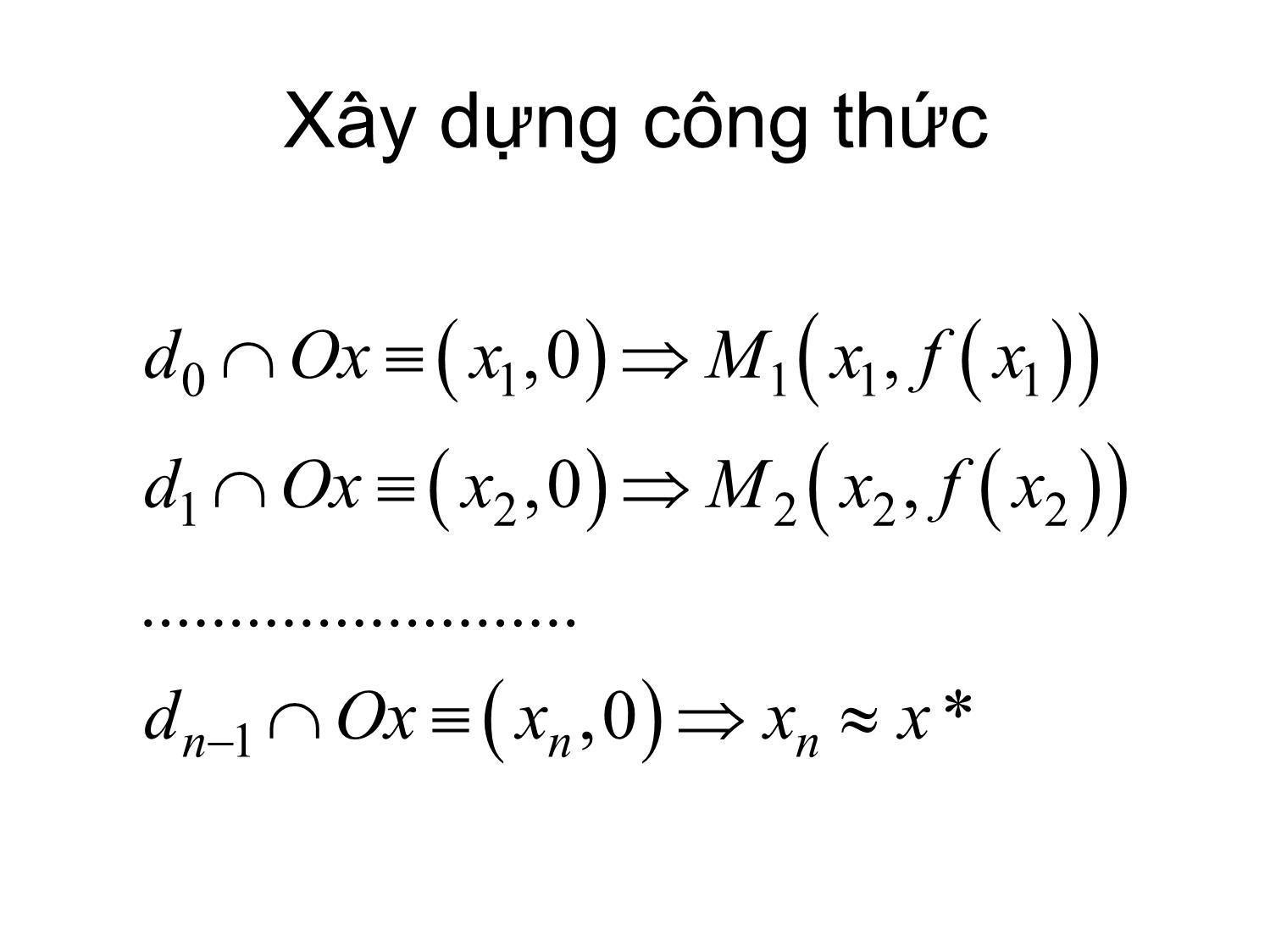
Trang 5

Trang 6

Trang 7
Trang 8
Trang 9

Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Phương pháp tính - Chương 4: Phương pháp tiếp tuyến giải phương trình f(x)=0 - Hà Thị Ngọc Yến", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Phương pháp tính - Chương 4: Phương pháp tiếp tuyến giải phương trình f(x)=0 - Hà Thị Ngọc Yến

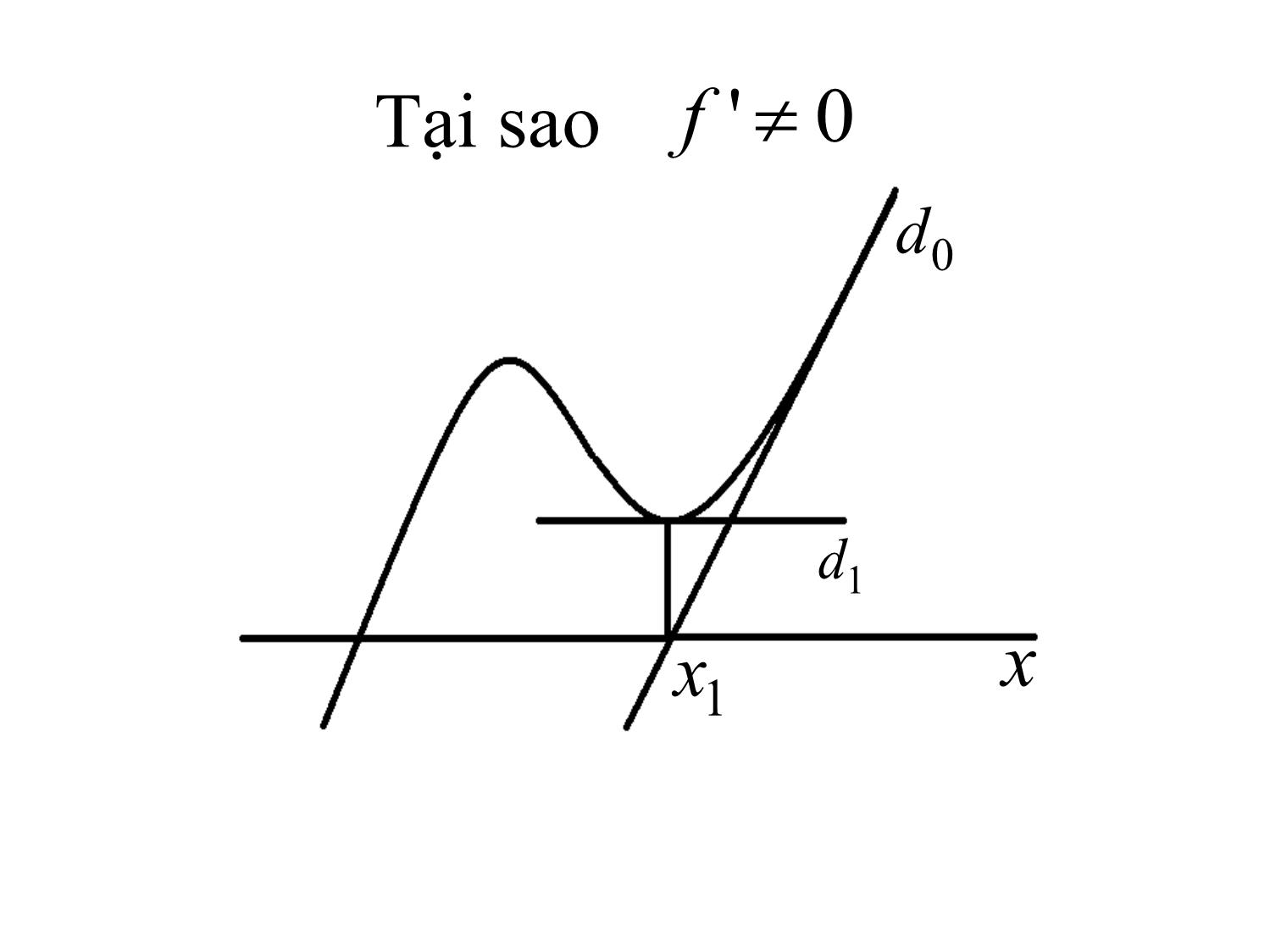
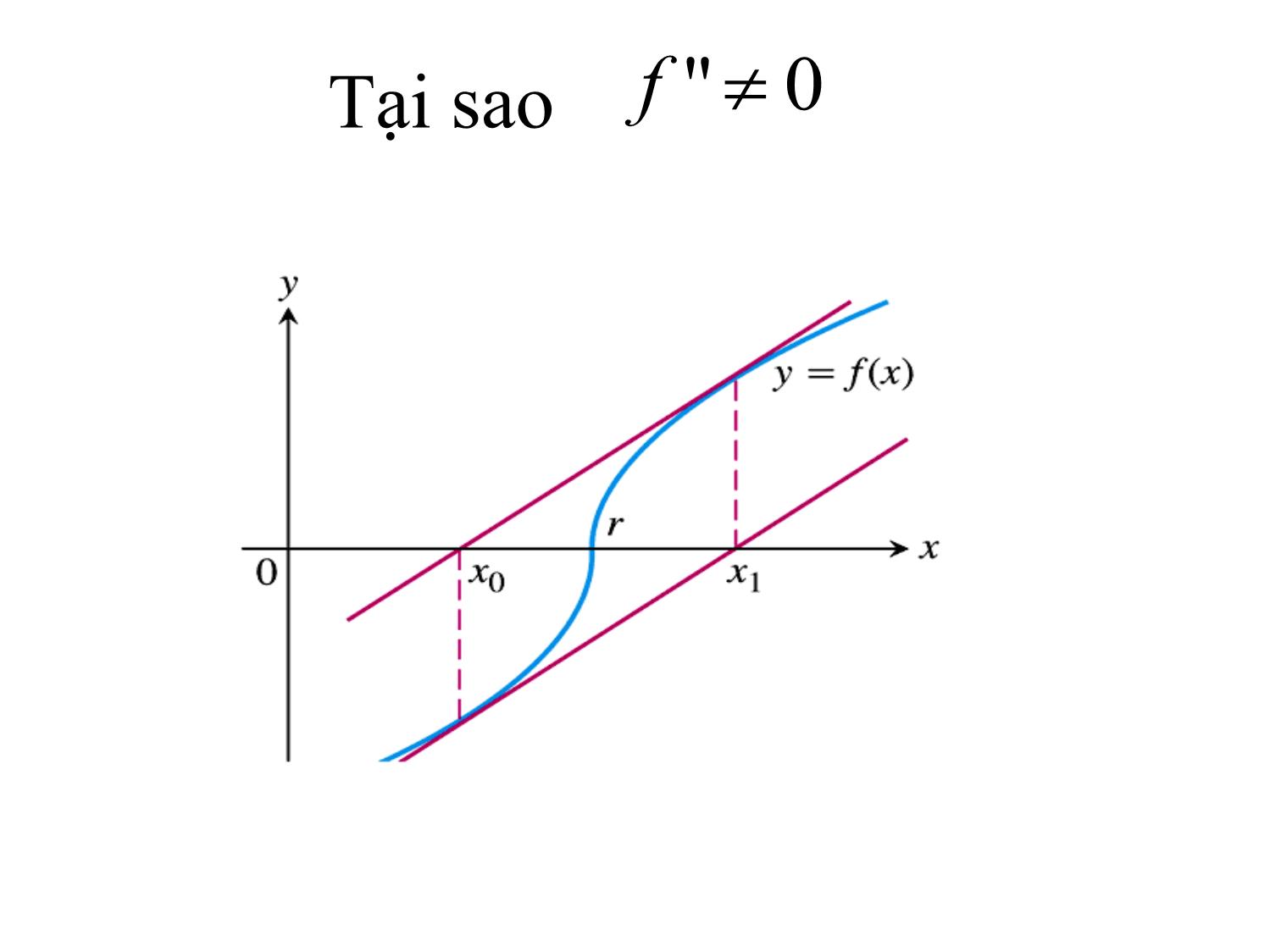
PHƯƠNG PHÁP TIẾP TUYẾN GIẢI PT f(x)=0 Hà Thị Ngọc Yến Hà nội, 9/2018 Ý tưởng phương pháp Ý tưởng phương pháp • Thay thế đường cong y f x trên [a,b] bằng TIẾP TUYẾN • Tìm giao điểm của dây cung với trục hoành thay cho giao điểm đường cong với trục hoành Xây dựng công thức Xét phương trình fx 0 và k.c.l nghiệm (a,b). Gọi M x , f x là điểm Fourie nếu f x f" x 0. Chọn điểm Fourie là điểm ban đầu, tức là Chọn x 0 : f x 0 f " x 0 0 và đặt M0 x 0,. f x 0 Gọi d k là tiếp tuyến với đồ thị hàm số tại M k . Xây dựng công thức dOxxMxfx01111 ,0, dOxxMxfx12222 ,0, ......................... dOxxxxnnn 1 ,0* Xây dựng công thức • Phương trình đường thẳng dk : y f'* xk x x k f x k • Vì dkk Ox x 1,0 nên ta có fx k xxkk 1 ** fx' k Sự hội tụ của phương pháp Điều kiện hội tụ: • (a,b) là khoảng cách ly nghiệm • ff', '' liên tục, xác định dấu không đổi trên [a,b] • Chọn đúng x0: f x 0 f " x 0 0. Tại sao f '0 d0 y d1 x1 x x Tại sao f "0 Định lý về sự hội tụ Với các điều kiện đã nêu trên dãy lặp (**) hội tụ đến nghiệm đúng của phương trình theo đánh giá sau fx n xxn *1 m1 M 2 2 xn x*2 x n x n 1 2m1 m12 minx a,, b f ' x ; M max x a b f " x CM Định lý về sự hội tụ • Các bước chứng minh: ➢ Dãy xn đơn điệu và bị chặn. ➢ Giới hạn của dãy là nghiệm của phương trình. ➢ Chứng minh các công thức sai số CM Định lý về sự hội tụ • Dãy xn đơn điệu : Trường hợp 1: f' x 0; f " x 0 x a ; b Xét điểm M t,,; f t t a b bất kỳ. Khi đó f x ht x 0 x a ; b , x x0 ht x :' f t x t f t CM Định lý về sự hội tụ • Ta có f" x 0 x a ; b f x0 0 • Mặt khác h x:' f x x x f x x0 0 0 0 h x 0 f x h x xx00 1 0 0 a x x,0 f x h x 1 0 1 x0 1 • Lý luận tương tự x1: f x 1 0 a x 2 x 1 , f x 2 0 CM Định lý về sự hội tụ • Giới hạn của dãy là nghiệm của phương trình • Gọi fx n 1 : limxxnn lim 1 nn fx' n 1 f f 0. f ' CT sai số mục tiêu • Ta có f xn f x n f f' c x n fx n fx n xn f' c m1 CT sai số theo hai xấp xỉ liên tiếp • Ta có: fc" 2 f x h x x x n xn 1 n2! n n 1 fc" 2 f' c x x x 11n2! n n M 2 2 xn x n x n 1 2m1 Thuật toán • Input: f,,, a b • Bước 1: Kiểm tra điều kiện ff', " xác định dấu không đổi trên, ab ; gán biến dấu cho dấu của f ". (Có thể làm thủ tục riêng cho bước này) • Bước 2: Chọn xa0 nếu f a .0 sign trái lại chọn xb0 . Thuật toán • Bước 3: Tính m1 (có thể làm gói riêng) • Bước 4: Tính fx 0 xx10 fx' 0 • Bước 5: Kiểm tra fx 1 m1 nếu thỏa mãn thì dừng, nếu không quay lại B4
File đính kèm:
 bai_giang_phuong_phap_tinh_chuong_4_phuong_phap_tiep_tuyen_g.pdf
bai_giang_phuong_phap_tinh_chuong_4_phuong_phap_tiep_tuyen_g.pdf

