Bài giảng Phương pháp tính - Chương 12: Các phương pháp Runge – Kutta hiện giải bài toán Cauchy cho phương trình vi phân thường - Hà Thị Ngọc Yến
R-K làm gì?
• Tính tích phân trong phương trình tích
phân qua s nấc trung gian
• Đảm bảo việc tính thông qua các nấc
trung gian có hiệu quả giống như khai
triển Taylor hàm y(x) đến bậc cao

Trang 1

Trang 2

Trang 3

Trang 4

Trang 5
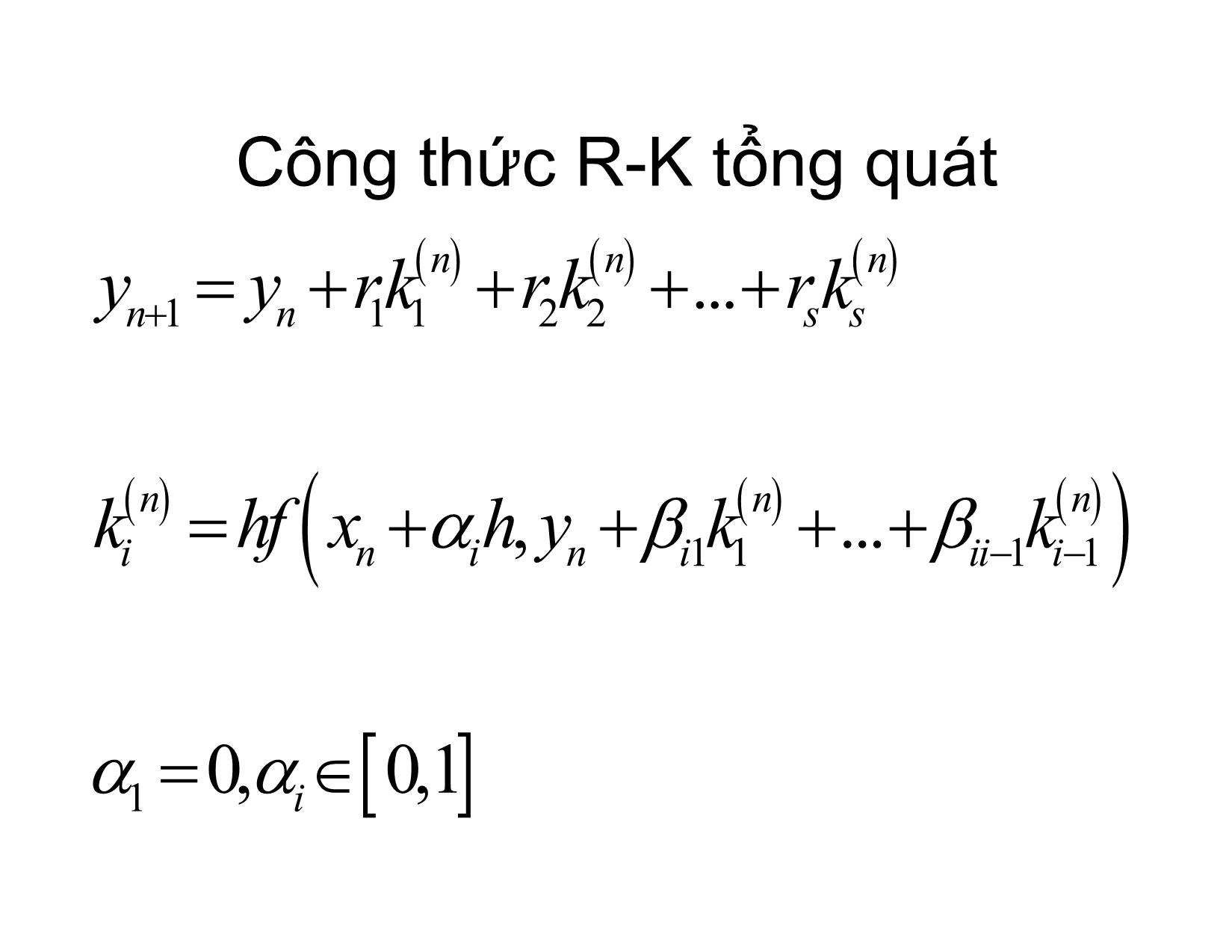
Trang 6
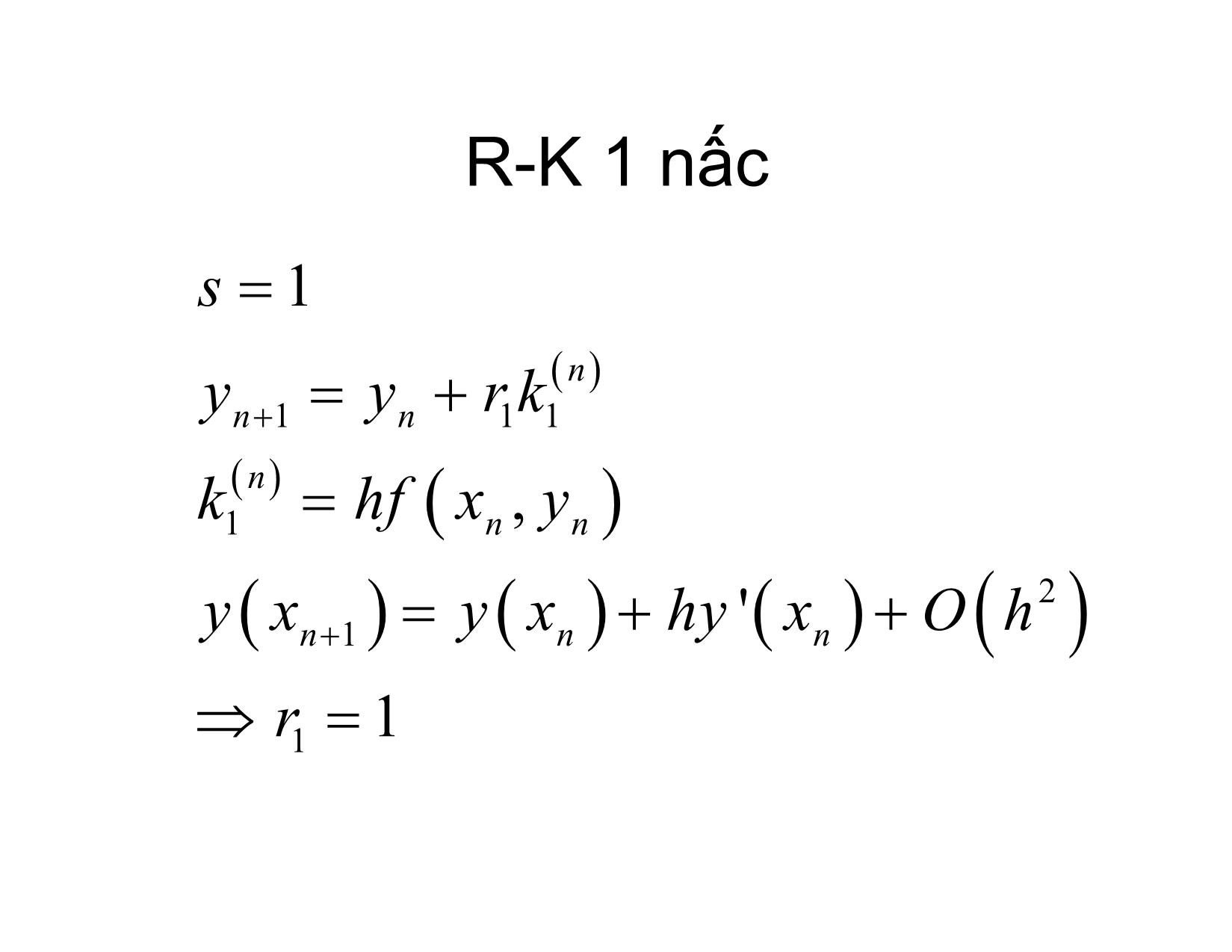
Trang 7

Trang 8
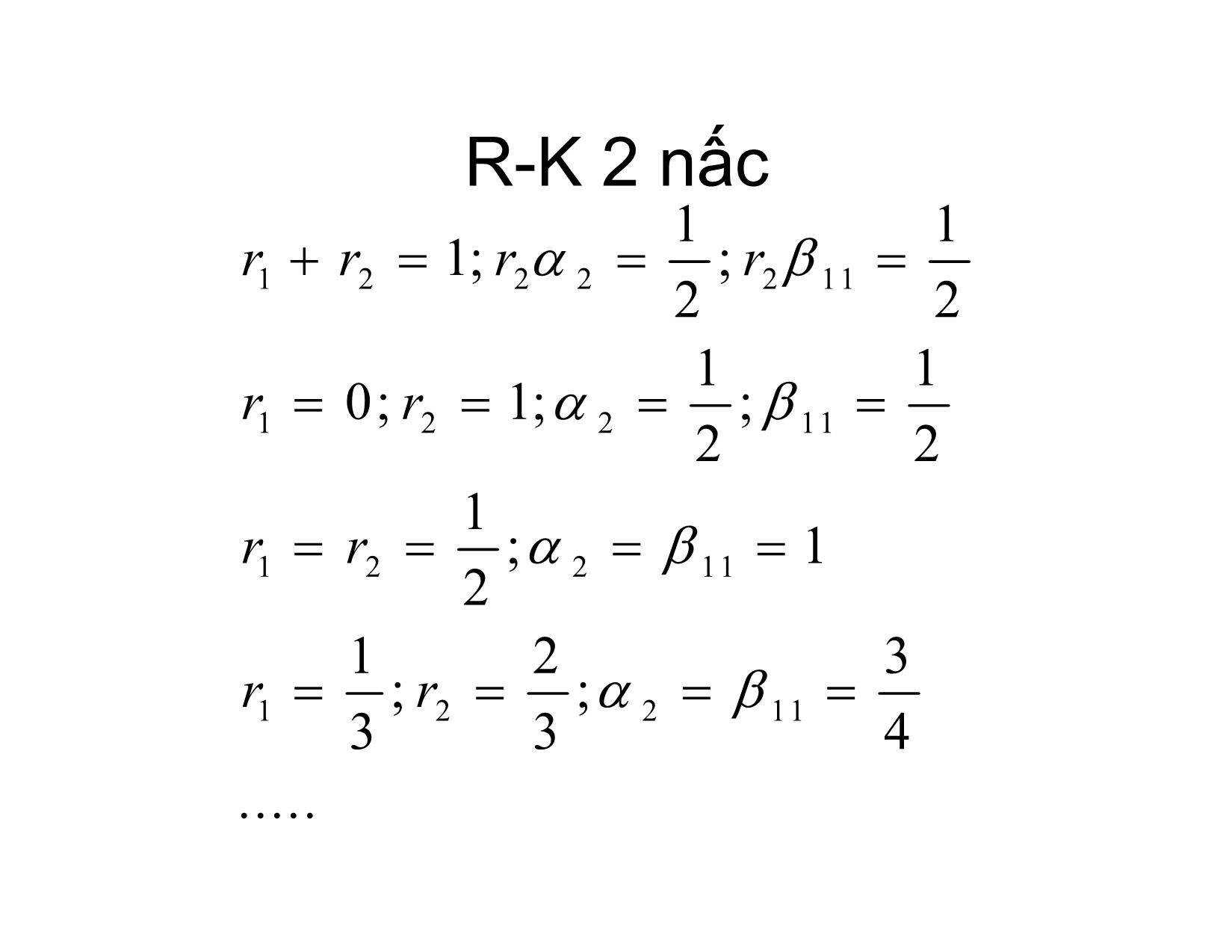
Trang 9
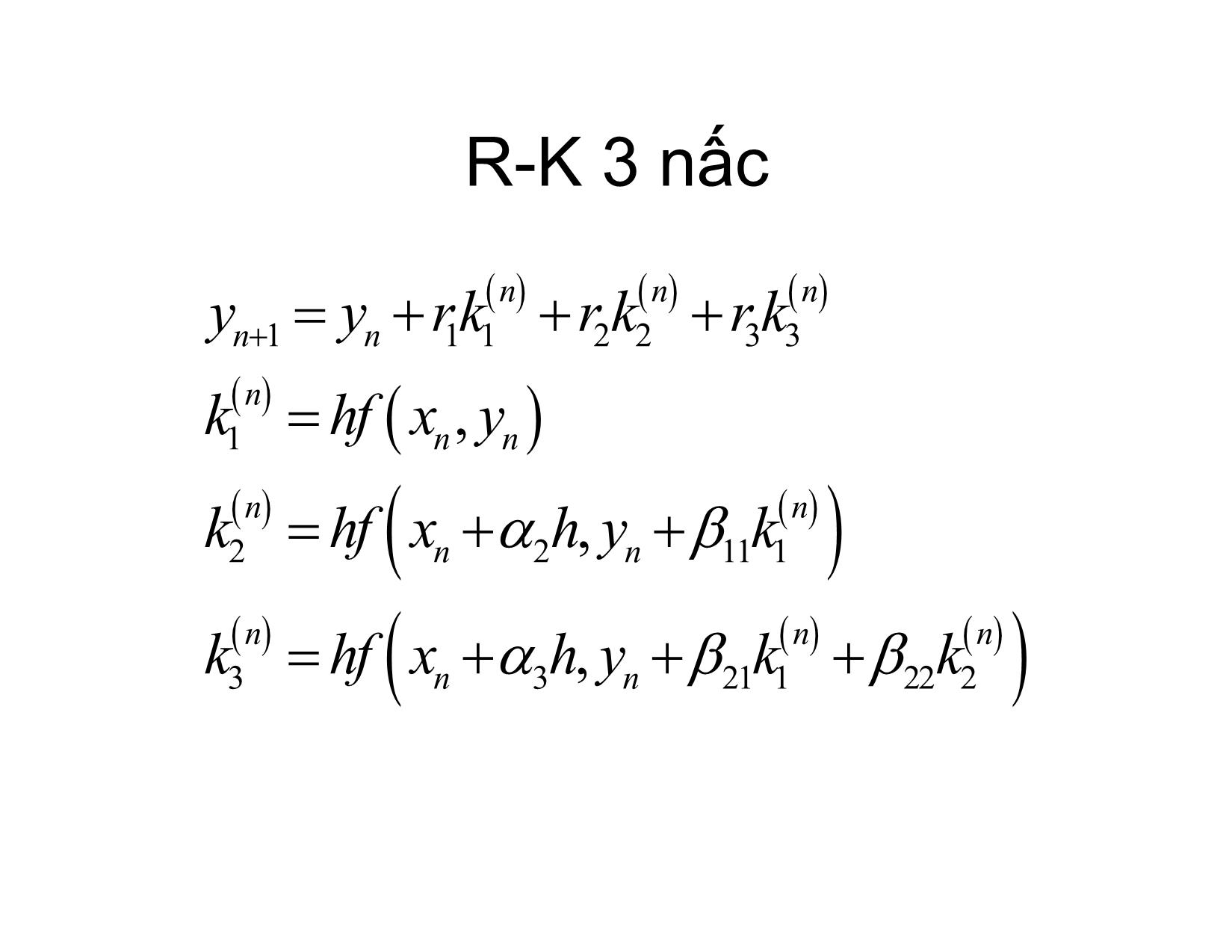
Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Phương pháp tính - Chương 12: Các phương pháp Runge – Kutta hiện giải bài toán Cauchy cho phương trình vi phân thường - Hà Thị Ngọc Yến", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Phương pháp tính - Chương 12: Các phương pháp Runge – Kutta hiện giải bài toán Cauchy cho phương trình vi phân thường - Hà Thị Ngọc Yến

Các pp Runge – Kutta hiện giải bài toán Cauchy cho phương trình vi phân thường Bài toán Cauchy yf'(,), x y xI xX0 ,, 1 k yCIR , yx() y 00 Phương trình tích phân x yx yx ftyt, dt 0 x0 xk 1 yx yx ftyt, dt kk 1 xk • Euler forward (hiện) yyhfxynn 1 (, nn ) • Euler backward (ẩn) yyhfxynn 111 nn, • Công thức hình thang h yynn 111 fxyfxy nnnn,, 2 R-K làm gì? • Tính tích phân trong phương trình tích phân qua s nấc trung gian • Đảmbảoviệc tính thông qua các nấc trung gian có hiệuquả giống như khai triển Taylor hàm y(x) đếnbậccao Công thứcR-K tổng quát nn n yyrkrkrknn 11122 ... ss nnn khfxhykininiiii , 11 ... 1 k 1 1 0,i 0,1 R-K 1 nấc s 1 n yyrknn 111 n khfxy1 nn, 2 yx nnn 1 yx hyx' Oh r1 1 R-K 2 nấc s 2 nn yyrkrknn 11122 n khfxyhf1 nn, n nn khfxhyk22111 nn , khfhfkfOh nn ''2 () 22,111, nxnyn 2 h '' 3 yx yx hf f f. f Oh nnnxnynn 1,,2 R-K 2 nấc 11 rr 1; r ; r 12 2222 211 11 rr 0; 1; ; 12 222 11 1 rr ;1 122 2 11 12 3 rr ;; 1233 211 4 ..... R-K 3 nấc nnn yyrkrkrknn 1112233 n khfxy1 nn, nn khfxhyk22111 nn , nnn khfxhyk33211222 nn , k R-K 3 nấc '' fhfhffnxnnyn 2, 11, n 22 kh2 hh2" 2 '' 2 2'' 3 2,fhxn 221, ff n xy 11, ffOh n yn 22 2 ''2'' nn h fhfknxn 3, 211 222 kf ynxx , 3 f n 2 kh3 2 hk nn kf '' k nn k fOh '' 3 3 21 1 22 2xy 21 1 22 2 yy h2 yx yx hf f'' f. f n 1 nn2 xnyn, n 3 h '' '' '' 2 ' ' '2 4 fffffffffOhxx xy n yy n y x y n 6 rrr123 1 1 rr 22 33 2 1 rr 2 11 3 21 22 2 111 rr 22 22622 33 1 rr 2 2 21 3 3 21 22 6 2221 rr2 11 3 21 22 6 1 22 2 6 1 11 22 6 R-K3 thường dùng 121 1 1 rr ;;; r ;1;; 1;2 123636 2 2 3112122 2 1 yy k nnn 4 kk nn 11236 n khfxy1 nn, nn 11 khfxhyk21 nn, 22 nnn khfxhykk312 nn,2 R-K3 thường dùng (Heun) 1312 rrr ;0;; ; ; 0 1234433 21132221 1 yy k nn 3 k nn 1134 n khfxy1 nn, nn 11 khfxhyk21 nn, 33 nn 22 khfxhyk32 nn, 33 R-K 4 thường dùng 1 yy kkkk nnnn22 nn 112346 n khfxy1 nn, nn 11 khfxhyk21 nn, 22 nn 11 khfxhyk32 nn, 22 nn khfxhyk43 nn, Bậc cao nhấtcủa các công thức R_K s nấc s 1 2 3 4 5 6 7 8 9 p 1 2 3 4 4 5 6 6 7 Ví dụ mô hình hệ thú mồi n xrn'1 ap K p' p anp
File đính kèm:
 bai_giang_phuong_phap_tinh_chuong_12_cac_phuong_phap_runge_k.pdf
bai_giang_phuong_phap_tinh_chuong_12_cac_phuong_phap_runge_k.pdf

