Bài giảng Mạng và hệ thống thông tin - Chương 1: Mở đầu về thuật toán và độ phức tạp - Nguyễn Văn Hạnh
Nội dung
1. Thuật toán và độ phức tạp
2. Đánh giá độ phức tạp thuật toán như thế nào?
3. Dùng O(f(n)) để đánh giá độ phức tạp của thuật toán
4. Các quy tắc để đánh giá độ phức tạp thuật toán
5. Các thuật toán cơ bản và độ phức tạp

Trang 1

Trang 2

Trang 3

Trang 4

Trang 5

Trang 6

Trang 7

Trang 8

Trang 9
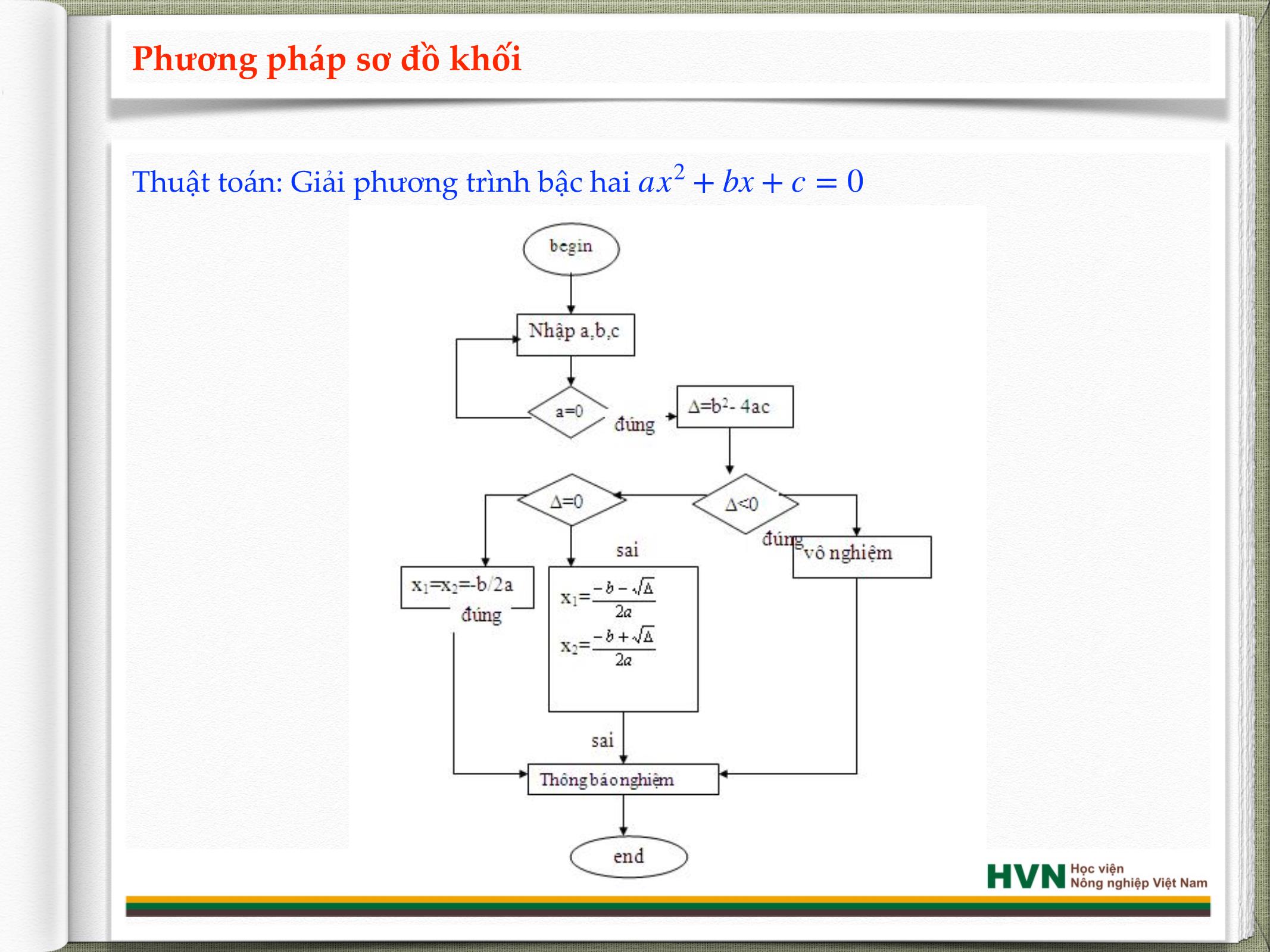
Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Mạng và hệ thống thông tin - Chương 1: Mở đầu về thuật toán và độ phức tạp - Nguyễn Văn Hạnh", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Mạng và hệ thống thông tin - Chương 1: Mở đầu về thuật toán và độ phức tạp - Nguyễn Văn Hạnh

Chương 1 Mở đầu về thuật toán và độ phức tạp Nguyễn Văn Hạnh Bộ môn Mạng và hệ thống thông tin Email: nvhanh@vnua.edu.vn Webpage: Nội dung 1. Thuật toán và độ phức tạp 2. Đánh giá độ phức tạp thuật toán như thế nào? 3. Dùng O(f(n)) để đánh giá độ phức tạp của thuật toán 4. Các quy tắc để đánh giá độ phức tạp thuật toán 5. Các thuật toán cơ bản và độ phức tạp Định nghĩa thuật toán • Thuật toán: là một dãy hữu hạn các bước, mỗi bước mô tả chính xác các phép toán, hoặc hành động cần thực hiện để cho ta lời giải của bài toán. • Ví dụ Thuật toán Euclid: Tìm UCLN của hai số nguyên dương. 1. Input: m, n là 2 số nguyên dương 2. Output: g (UCLN của m và n) 3. Phương pháp: Bước 1: Tìm r, phân dư của phép chia m cho n. Bước 2: Nếu r = 0, thì g := n (gán giá trị của n cho g) và dừng lại. Ngược lại (r ≠ 0), thì m := n; n := r và quay lại bước 1. Các yêu cầu về thuật toán 1. Input: là các giá trị cần đưa vào khi thuật toán bắt đầu làm việc. Ví dụ trong thuật toán Euclid, input là 2 số nguyên dương m, n . 2. Output: là các giá trị có quan hệ hoàn toàn xác định với các dữ liệu input, và là kết quả của sự thực hiện thuật toán. Ví dụ trong thuật toán Euclid, output là UCLN g . 3. Tính xác định: Ở mỗi bước, các thao tác phải rõ ràng, không gây nên sự nhập nhằng. Thuật toán cần được mô tả trong các ngôn ngữ lập trình: các mệnh đề được tạo theo các quy tắc cú pháp nghiêm ngặt và chỉ có một nghĩa duy nhất. 4. Tính khả thi: các phép toán có thể được thực hiện trực tiếp. 5. Tính dừng: thuật toán phải dừng sau một số hữu hạn bước thực hiện. Vấn đề giải được và không giải được 1. Vấn đề giải được: là vấn đề có thuật toán giải. Ví dụ, tìm nghiệm của hệ phương trình tuyến tính là vấn đề giải được. 2. Vấn đề không giải được: là vấn đề không tồn tại thuật toán giải. Ví dụ, thuật toán chắc thắng cho người thứ 2 của cờ ca rô; thuật toán xác định xem một máy Turing có dừng lại sau n bước hay không. Các vấn đề liên quan đến thuật toán 1. Thiết kế thuật toán: một số kỹ thuật thiết kế thuật toán: • Phương pháp chia để trị (divide-and-conque) • Phương pháp tham lam (greedy method) • Phương pháp quy hoạch động 2. Tính đúng đắn của thuật toán: khi thuật toán được thực hiện sẽ cho kết quả đúng với mọi dữ liệu vào hợp lệ. 3. Phân tích thuật toán: với một bài toán có một số thuật giải → cần phân tích, đánh giá độ phức tạp của thuật toán để lựa chọn thuật toán nào. Đánh giá hiệu quả của thuật toán Hai tiêu chuẩn để lựa chọn thuật toán: Thuật toán đơn giản, dễ hiểu, dễ cài đặt (dễ viết chương trình) Thuật toán sử dụng tiết kiệm nhất các nguồn tài nguyên của máy tính, chạy nhanh nhất có thể được: tính hiệu quả của thuật toán: • Dung lượng không gian nhớ cần thiết để lưu các dữ liệu vào, các kết quả tính toán trung gian và kết quả của thuật toán. • Thời gian để thực hiện thuật toán: một thuật toán hiệu quả nếu có thời gian chạy ít hơn so với các thuật toán khác. Biểu diễn thuật toán Phương pháp biểu diễn thuật toán: • Phương pháp liệt kê từng bước • Phương pháp sơ đồ khối • Ngôn ngữ lập trình Phương pháp liệt kê từng bước Thuật toán: Giải phương trình bậc hai ax2 + bx + c = 0 • Bước 1: Xác định các hệ số a, b, c • Bước 2: Kiểm tra các hệ số a, b, c có khác 0 hay không? Nếu a = 0 quay lại thực hiện bước 1. • Bước 3: Tính Δ = b2 − 4ac • Bước 4: Nếu Δ < 0 thông báo PT vô nghiệm và chuyển sang bước 8 −b • Bước 5: Nếu Δ = 0, tính x = x = và chuyển sang bước 7 1 2 2a −b ∓ Δ • Bước 6: Tính x = và chuyển sang bước 7 1,2 2a • Bước 7: Thông báo các nghiệm x1, x2 • Bước 8: Kết thúc thuật toán Phương pháp sơ đồ khối Thuật toán: Giải phương trình bậc hai ax2 + bx + c = 0 Ngôn ngữ lập trình Python Thuật toán: Giải phương trình bậc hai ax2 + bx + c = 0 Độ phức tạp của thuật toán Tại sao lại cần thuật toán có hiệu quả? • Đối với một vấn đề có thể có nhiều thuật toán giải, trong số đó có thể thuật toán này hiệu quả hơn thuật toán kia (chạy nhanh hơn). Đánh giá thời gian thực hiện thuật toán như thế nào? 1. Phương pháp thử nghiệm: viết chương trình và cho chạy chương trình với các dữ liệu vào khác nhau trên một máy tính nào đó. Thời gian chạy chương trình phụ thuộc vào các nhân tố: • Các dữ liệu vào • Chương trình dịch để chuyển chương trình thành mã máy • Tốc độ thực hiện các phép toán của máy tính được sử dụng → không thể biểu diễn chính xác thời gian chạy là bao nhiêu đơn vị thời gian chuẩn. Độ phức tạp của thuật toán Đánh giá thời gian thực hiện thuật toán như thế nào? 2. Phương pháp lý thuyết: • Ta sẽ coi thời gian thực hiện thuật toán như là hàm số của cỡ dữ liệu vào. • Cỡ của dữ liệu vào là một tham số đặc trưng cho dữ liệu vào, có ảnh hưởng quyết định đến thời gian thực hiện chương trình. Thông thường cỡ của dữ liệu vào là một số nguyên dương n. • Ta sẽ sử dụng hàm số T(n), trong đó n là cỡ dữ liệu vào, để biểu diễn thời gian thực hiện một thuật toán. • Thời gian thực hiện T(n) là số phép toán sơ cấp cần phải tiến hành khi thực hiện thuật toán. Ví dụ các phép toán số học +, − , * , / và các phép toán so sánh = , , ≤ , ≥ là các phép toán sơ cấp. Độ phức tạp của thuật toán Ví dụ: xét bài toán xác định một đối tượng a có trong danh sách n phần tử (a1, a2, , an). • So sánh a với từng phần tử có trong danh sách đi từ đầu tới cuối danh sách • Khi gặp phần tử ai đầu tiên thoả mãn ai = a thì dừng lại • Hoặc khi đến cuối danh sách mà không gặp ai nào bằng a thì trong trường hợp này a không có trong danh sách. • Các dữ liệu vào là a và danh sách (a1, a2, , an). Cỡ của dữ liệu vào là n . • Nếu xem thời gian thực hiện T(n) là số các phép so sánh, ta có T(n) ≤ n. • T(n) = n là độ phức tạp của thuật toán trong trường hợp xấu nhất. • Độ phức tạp trung bình của thuật toán là thời gian trung bình Ttb(n) trên tất cả các dữ liệu vào cỡ n . Dùng O(f(n)) để đánh giá độ phức tạp của thuật toán Định nghĩa • Giả sử n là số nguyên dương. T(n) và f(n) là các hàm thực không âm. Ta viết T(n) = O(f(n)) nếu và chỉ nếu tồn tại các hằng số dương c, n0 sao cho T(n) ≤ cf(n), với mọi n ≥ n0. • Nếu một thuật toán có độ phức tạp T(n) = O(f(n)), ta nói thuật toán có độ phức tạp cấp f(n). Ví dụ: Giả sử T(n) = 3n2 + 4n + 5. Ta có T(n) ≤ 3n2 + 4n2 + 5n2 = 12n2, với mọi n ≥ 1. Vậy T(n) = O(n2): thuật toán có độ phức tạp cấp n2 Dùng O(f(n)) để đánh giá độ phức tạp của thuật toán Tính chất • Nếu T(n) = O(f(n)) và f(n) = O(g(n)) thì T(n) = O(g(n)). • Thật vậy, T(n) = O(f(n)) và f(n) = O(g(n)) nên tồn tại c1, c2, n1, n2 để T(n) ≤ c1 f(n) với mọi n ≥ n1 và f(n) ≤ c2g(n) với mọi n ≥ n2. • Khi đó T(n) ≤ c1c2g(n) với mọi n ≥ n0 = max(n1, n2). Nên ta có T(n) = O(g(n)). • Khi biểu diễn cấp của độ phức tạp thuật toán bởi hàm f(n), ta sẽ chọn f(n) là hàm nhỏ nhất, đơn giản nhất có thể sao cho T(n) = O(f(n)). Dùng O(f(n)) để đánh giá độ phức tạp của thuật toán Danh sách sắp xếp theo thứ tự tăng dần của độ phức tạp thuật toán Dùng O(f(n)) để đánh giá độ phức tạp của thuật toán Ví dụ: 2 • Thuật toán A có độ phức tạp TA(n) = O(n ), thuật toán B có độ phức tạp TB(n) = O(nlogn). • Với n = 1024, thuật toán A cần 1048576 phép toán sơ cấp, còn thuật toán B cần 10240 phép toán sơ cấp. • Nếu cần 1 micro-giây cho một phép toán sơ cấp thì thuật toán A cần khoảng 1,05 giây, thuật toán B cần khoảng 0,01 giây. • Với n = 1024x2 = 2048 thì thuật toán A cần khoảng 4,2 giây, thuật toán B cần khoảng 0,02 giây. • Với n càng lớn thì thuật toán A càng đòi hỏi thời gian thực hiện nhiều hơn rất nhiều so với thuật toán B. Các quy tắc để đánh giá độ phức tạp của thuật toán Quy tắc tổng: Nếu T1(n) = O( f1(n)) và T2(n) = O( f2(n)) thì T1(n) + T2(n) = O(max( f1(n), f2(n))) • Áp dụng: Giả một thuật toán được phân thành 3 phần với độ phức tạp của 2 từng phần lần lượt là T1(n) = O(1); T2(n) = O(n ) và T3(n) = O(n). Khi đó độ phức tạp của thuật toán là: 2 2 T(n) = T1(n) + T2(n) + T3(n) = O(max(1,n , n)) = O(n ) Quy tắc để đánh giá độ phức tạp của các câu lệnh đơn, khối 1. Câu lệnh (đơn): các phép gán, đọc, viết, goto có độ phức tạp O(1). 2. Lệnh hợp thành (hoặc khối): S1, S2, , Sn là câu lệnh thì Begin S1, S2, , Sn End gọi là lệnh hợp thành: Độ phức tạp được xác định bằng luật tổng. Quy tắc để đánh giá độ phức tạp của câu lệnh If 3. Lệnh If: S1, S2 là các câu lệnh có độ phức tạp O( f1(n)), O( f2(n)), E là biểu thức logic: If E then S1 và If E then S1 else S2 gọi là lệnh If và có độ phức tạp là O(max( f1(n), f2(n))) Quy tắc để đánh giá độ phức tạp của câu lệnh Case 4. Lệnh Case: S1, , Sk là các câu lệnh có độ phức tạp O( f1(n)), , O( fk(n)), E là biểu thức có kiểu thứ tự đếm được và v1, , vk là các giá trị có cùng kiểu với E: Case E of v1 : S1; vk : Sk; End gọi là lệnh Case và có độ phức tạp là O(max( f1(n), , fk(n))) Quy tắc để đánh giá độ phức tạp của câu lệnh While 5. Lệnh While: Nếu S là các câu lệnh có độ phức tạp O( f(n)), E là biểu thức logic: While E do S gọi là lệnh While. Nếu g(n) là số tối đa các lần thực hiện lệnh S khi thực hiện lệnh While thì độ phức tạp của lệnh While là O( f(n)g(n)). Quy tắc để đánh giá độ phức tạp của câu lệnh Repeat 6. Lệnh Repeat: Nếu S là các câu lệnh có độ phức tạp O( f(n)), E là biểu thức logic: Repeat S Until E gọi là lệnh Repeat. Nếu g(n) là số tối đa các lần lặp thì độ phức tạp của lệnh Repeat là O( f(n)g(n)). Quy tắc để đánh giá độ phức tạp của câu lệnh For 7. Lệnh For: Nếu S là các câu lệnh có độ phức tạp O( f(n)), E1, E2 là biểu thức cùng một kiểu thứ tự đếm được thì: For i := E1 to E2 do S hoặc For i := E2 downto E1 do S gọi là lệnh For. Nếu g(n) là số tối đa các lần lặp thì độ phức tạp của lệnh For là O( f(n)g(n)). Quy tắc để đánh giá độ phức tạp của hàm đệ quy 8. Hàm đệ quy: Giả sử độ phức tạp của hàm đệ quy là T(n) với n là cỡ dữ liệu vào. • Khi đó độ phức tạp của các lời gọi đệ quy thủ tục là T(m); với m < n. • Đánh giá độ phức tạp T(n0), với n0 là cỡ dữ liệu vào nhỏ nhất có thể được. • Đánh giá thân của hàm để nhận được quan hệ đệ quy như sau T(n) = F(T(n1), T(n2), , T(nk)) với n1, n2, , nk < n • Giải phương trình đệ quy này ta sẽ nhận được sự đánh giá của T(n). Ví dụ đánh giá độ phức tạp của hàm đệ quy Ví dụ: Đánh giá độ phức tạp của hàm đệ quy để tính n! Function fact(n); Begin If n ≤ 1 then fact := 1 Else fact := n*fact(n-1); End; • Độ phức tạp là T(n) với n là cỡ dữ liệu vào. • Với n = 1: T(1) = O(1) vì chỉ thực hiện lệnh gán fact := 1 • Với n > 1: T(n) sẽ là O(1) để thực hiện phép gán (:=) và phép nhân (*) cộng với T(n-1) là độ phức tạp của lời gọi đệ quy fact(n-1). Nên ta có: T(1) = C1; T(n) = C2 + T(n-1); Ví dụ đánh giá độ phức tạp của hàm đệ quy Ví dụ: Đánh giá độ phức tạp của hàm đệ quy để tính n! Function fact(n); Begin If n ≤ 1 then fact := 1 Else fact := n*fact(n-1); End; • Khi đó T(n) = C2 + T(n-1) = C2 + C2 + T(n-2) = C2 + C2 + C2 + T(n-3) = = (n-1)C2 + T(1) = (n-1)C2 + C1 • Vậy T(n) = O(n) Ví dụ xác định độ phức tạp của thuật toán Ví dụ: Xác định độ phức tạp của thuật toán tính dãy số Fibonacci Công thức truy hồi của dãy Fibonacci là: Bài toán áp dụng: Một đôi thỏ (gồm một thỏ đực và một thỏ cái) cứ mỗi tháng đẻ được một đôi thỏ con (cũng gồm một thỏ đực và thỏ cái); một đôi thỏ con, khi tròn 2 tháng tuổi, sau mỗi tháng đẻ ra một đôi thỏ con, và quá trình sinh nở cứ thế tiếp diễn. Hỏi sau n tháng có bao nhiêu đôi thỏ, nếu đầu năm (tháng Giêng) có một đôi thỏ sơ sinh? Ví dụ xác định độ phức tạp của thuật toán Ví dụ: Xác định độ phức tạp của thuật toán tính dãy số Fibonacci Function Fibo(n: integer): integer; Var i, j, k: integer; Begin i := 1; j :=0; For k := 1 to n do Begin j := i + j; i := j - i; End; Fibo := j; End; Độ phức tạp của thuật toán trên là O(n). Ví dụ so sánh độ phức tạp của 2 thuật toán Ví dụ: Xét bài toán tính giá trị của đa thức n n−1 P(x) = anx + an−1x + + a1x + a0 tại x = x0 Thuật toán 1: Bước 1. Tính giá trị của từng hạng tử: với i = 1 đến n tính i aix0 n Bước 2. Tính i P(x0) = ∑ aix0 + a0 i=1 Thuật toán 2: Ta viết n−1 n−2 P(x) = (anx + an−1x + + a1)x + a0 = . . . = ((anx + an−1)x)x + a0 Bước 1. Gán P := an Bước 2. Với i = 1 đến n: gán P = Px0 + an−i Bước 3. Gán kết quả P(x0) = P Độ phức tạp của thuật toán 1 Thuật toán 1: Bước 1. Tính giá trị của từng hạng tử: với i = 1 đến n tính i aix0 i = 1 : ta phải thực hiện 1 phép nhân: a1 . x0 ta phải thực hiện 2 phép nhân 2 i = 2 : a2x0 = a2 . x0 . x0 ta thực hiện n phép nhân: n i = n : anx0 = an . x0x0 n(n + 1) Vậy bước 1 ta phải thực hiện 1 + 2 + + n = phép nhân. 2 n Bước 2. Tính i : ta thực hiện phép cộng. P(x0) = ∑ aix0 + a0 n i=1 n(n + 1) n(n + 3) Vậy thuật toán 1 cần + n = phép tính nên độ phức tạp của thuật 2 2 toán 1 là O(n2) . Độ phức tạp của thuật toán 2 Thuật toán 2: Bước 1. Gán P := an : ta thực hiện một phép toán Bước 2. Với i = 1 đến n: gán P = Px0 + an−i : ta phải thực hiện n lần, mỗi lần cần thực hiện 3 phép toán là 1 phép nhân và một phép cộng và 1 phép gán nên bước 2 cần thực hiện 3n phép toán. Bước 3. Gán kết quả P(x0) = P: ta thực hiện 1 phép toán Vậy thuật toán 2 cần thức hiện 3n + 2 phép toán nên độ phức tạp của thuật toán 2 là O(n) . Kết luận: Thời gian thực hiện thuật toán 2 ít hơn thời gian thực hiện thuật toán 1. Bài tập về nhà Hãy xây dựng và đánh giá độ phức tạp của các thuật toán sau: 1. Thuật toán tìm phần tử lớn nhất của một dãy hữu hạn số thực 2. Thuật toán tìm phần tử bé nhất của một tập con của tập hợp các số tự nhiên 3. Thuật toán xếp lại một dãy theo thứ tự tăng dần 4. Thuật toán tìm một dãy các số liên tiếp nhau (dài nhất có thể) có tổng dương trong một dãy số thực cho trước. The end of chapter 1
File đính kèm:
 bai_giang_mang_va_he_thong_thong_tin_chuong_1_mo_dau_ve_thua.pdf
bai_giang_mang_va_he_thong_thong_tin_chuong_1_mo_dau_ve_thua.pdf

