Bài giảng Kiến trúc máy tính - Tuần 9: Phép toán số học trên máy tính (Tiếp theo)
Định nghĩa:
Biểu diễn số thực:
Scientific notation: Một số thực được gọi là “scientific notation” khi bên trái dấu chấm có đúng 1 chữ số.
Normalized number: Một số thực được gọi là “Normalized number” (dạng chuẩn) khi số này được viết trong “scientific notation” và chữ số bên trái dấu chấm không phải là 0.
Ví dụ: 1.0ten x 10-9: số thực chuẩn
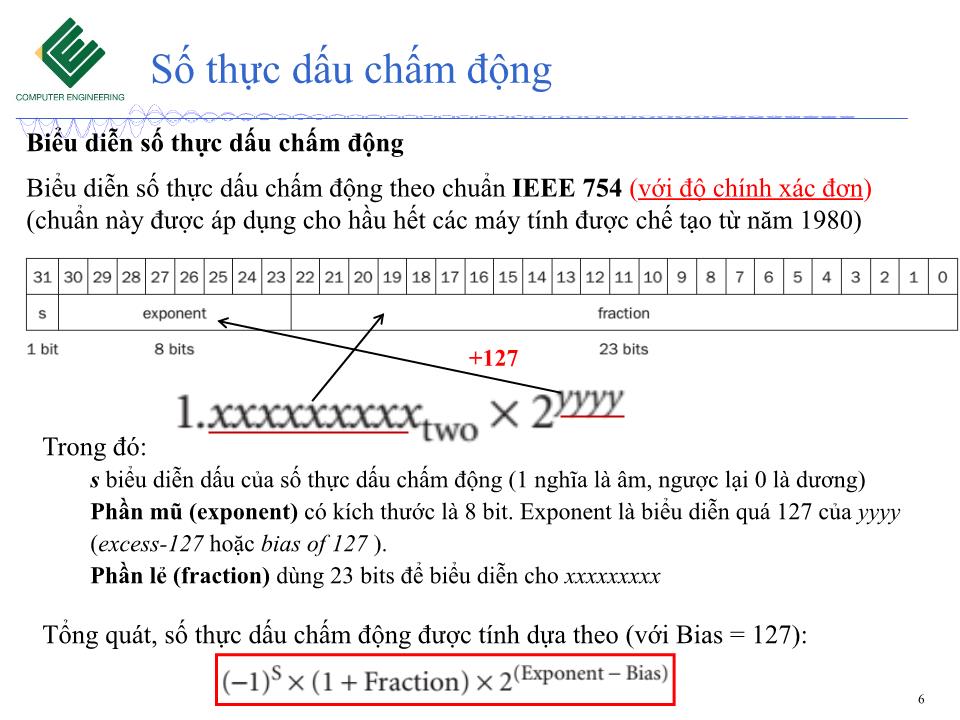
0.1ten x 10-8: không phải số thực chuẩn
10.0ten x 10-10: không phải số thực chuẩn

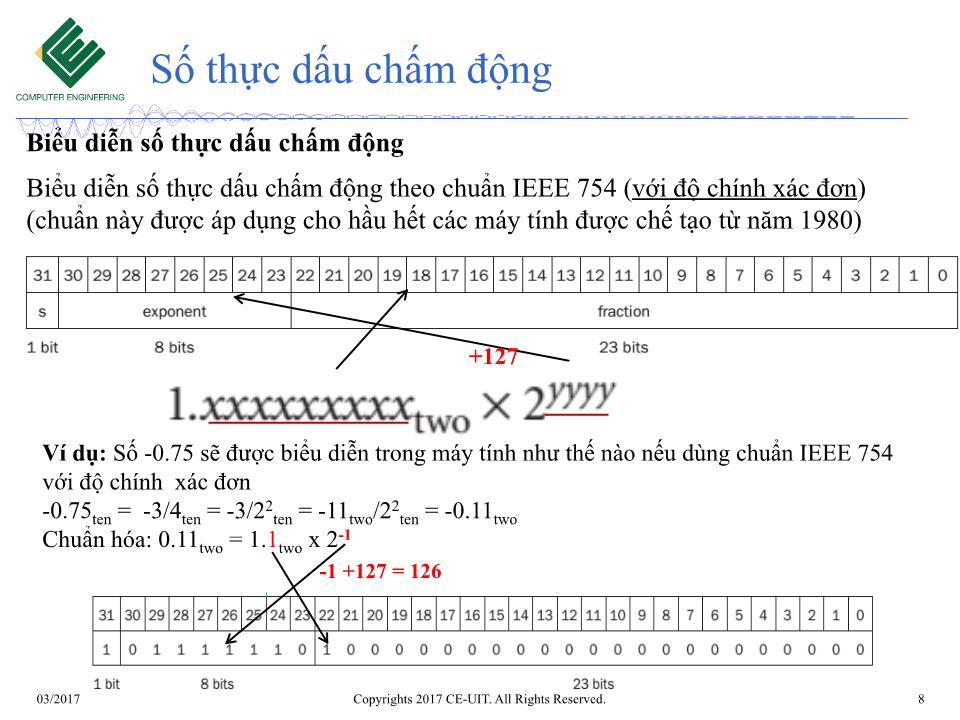
Trang 1

Trang 2

Trang 3

Trang 4

Trang 5
Trang 6

Trang 7
Trang 8

Trang 9

Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Kiến trúc máy tính - Tuần 9: Phép toán số học trên máy tính (Tiếp theo)", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Kiến trúc máy tính - Tuần 9: Phép toán số học trên máy tính (Tiếp theo)

Tuần 9 PHÉP TOÁN SỐ HỌC TRÊN MÁY TÍNH (Tiếp theo) 03/2017 Copyrights 2017 CE-UIT. All Rights Reserved. 1 KIẾN TRÚC MÁY TÍNH PHÉP TOÁN SỐ HỌC TRÊN MÁY TÍNH 2 Mục tiêu: Hiểu các phép toán số học trên số nguyên và số thực dấu chấm động trong máy tính. Với số nguyên: Hiểu các phép toán cộng, trừ, nhân và chia Cách thiết kế mạch nhân và chia Với số thực dấu chấm động: Hiểu các phép toán cộng, trừ và nhân Cách thiết kế mạch nhân 03/2017 Copyrights 2017 CE-UIT. All Rights Reserved. Slide được dịch và các hình được lấy từ sách tham khảo: Computer Organization and Design: The Hardware/Software Interface , Patterson, D. A., and J. L. Hennessy, Morgan Kaufman, Revised Fourth Edition, 2011 . PHÉP TOÁN SỐ HỌC TRÊN MÁY TÍNH Giới thiệu Phép cộng & P hép trừ Phép nhân Phép chia Số thực dấu chấm động 3 03/2017 Copyrights 2017 CE-UIT. All Rights Reserved. Số thực dấu chấm động Định nghĩa: 4 Biểu diễn số thực: Scientific notation: Một số thực được gọi là “scientific notation” khi bên trái dấu chấm có đúng 1 chữ số. Normalized number: Một số thực được gọi là “ Normalized number ” (dạng chuẩn) khi số này được viết trong “scientific notation” và chữ số bên trái dấu chấm không phải là 0. Ví dụ: 1.0 ten x 10 -9 : số thực chuẩn 0.1 ten x 10 -8 : không phải số thực chuẩn 10.0 ten x 10 -10 : không phải số thực chuẩn 03/2017 Copyrights 2017 CE-UIT. All Rights Reserved. Số thực dấu chấm động Định nghĩa: 5 Trong máy tính, các số nhị phân phải được đưa về dạng chuẩn như sau : 03/2017 Copyrights 2017 CE-UIT. All Rights Reserved. Số thực dấu chấm động Biểu diễn số thực dấu chấm động Biểu diễn số thực dấu chấm động theo chuẩn IEEE 754 ( với độ chính xác đơn ) (chuẩn này được áp dụng cho hầu hết các máy tính được chế tạo từ năm 1980) 6 Trong đó: s biểu diễn dấu của số thực dấu chấm động (1 nghĩa là âm, ngược lại 0 là dương) Phần mũ (exponent) có kích thước là 8 bit. Exponent là biểu diễn quá 127 của yyyy ( excess-127 hoặc bias of 127 ). Phần lẻ (fraction) dùng 23 bits để biểu diễn cho xxxxxxxxx Tổng quát, số thực dấu chấm động được tính dựa theo (với Bias = 127): +127 Số thực dấu chấm động Biểu diễn số thực dấu chấm động Biểu diễn số thực dấu chấm động theo chuẩn IEEE 754 ( với độ chính xác đơn ) (chuẩn này được áp dụng cho hầu hết các máy tính được chế tạo từ năm 1980) 7 Tổng quát, số thực dấu chấm động được tính dựa theo: Hoặc: ( với s1, s2, s3 là các bit lần lượt từ trái sang phải của fraction) +127 03/2017 Copyrights 2017 CE-UIT. All Rights Reserved. Số thực dấu chấm động Biểu diễn số thực dấu chấm động Biểu diễn số thực dấu chấm động theo chuẩn IEEE 754 ( với độ chính xác đơn ) (chuẩn này được áp dụng cho hầu hết các máy tính được chế tạo từ năm 1980) 8 +127 Ví dụ: Số -0.75 sẽ được biểu diễn trong máy tính như thế nào nếu dùng chuẩn IEEE 754 với độ chính xác đơn -0.75 ten = -3/4 ten = -3/2 2 ten = -11 two /2 2 ten = -0.11 two Chuẩn hóa: 0.11 two = 1. 1 two x 2 -1 -1 +127 = 126 03/2017 Copyrights 2017 CE-UIT. All Rights Reserved. Số thực dấu chấm động Ví dụ: Cho biểu diễn số dấu chấm động với độ chính xác đơn như hình sau, hỏi số tương ứng với biểu diễn này trong hệ thập phân là bao nhiêu? 9 Trả lời: b it dấu s là 1 e xponent chứa 129 Số tương ứng : (−1) s × (1+ fraction) × 2 (exponent – 127) = (−1) 1 × (1+ 0.01) × 2 (129 – 127) = (−1.01 × 2 2 ) two = −5.0 ten 03/2017 Copyrights 2017 CE-UIT. All Rights Reserved. Số thực dấu chấm động Biểu diễn số thực dấu chấm động Tràn trên (Overflow): trường hợp này xảy ra khi kích thước của số mũ lớn hơn kích thước giới hạn trên (số mũ dương). Tràn dưới (Underflow): trường hợp này xảy ra khi kích thước của số mũ nhỏ hơn kích thước giới hạn dưới (số mũ âm). Nhằm hạn chế việc tràn trên hoặc tràn dưới về số mũ, IEEE 754 giới thiệu thêm một cách biểu diễn số thực dấu chấm động, vơí trường exponent mở rộng lên tới 11 bits. Cách biểu diễn này gọi là IEEE 754 với độ chính xác kép Độ chính xác đơn (Single precision): một số thực dấu chấm động được biểu diễn ở dạng 32 bit . Độ chính xác kép (Double precision): một số thực dấu chấm động được biểu diễn ở dạng 64 bit. Chú ý: Trong lập trình ngôn ngữ C, các số thực dạng float sẽ được định dạng theo kiểu độ chính xác đơn, còn các số dạng double sẽ được định dạng theo kiểu độ chính xác kép 10 03/2017 Copyrights 2017 CE-UIT. All Rights Reserved. Số thực dấu chấm động Biểu diễn số thực dấu chấm động Biểu diễn số thực dấu chấm động theo chuẩn IEEE 754 ( với độ chính xác kép ) 11 Trong đó: s biểu diễn dấu của số thực dấu chấm động (1 nghĩa là âm, ngược lại 0 là dương) Phần mũ (exponent) có kích thước là 11 bits. Exponent là biểu diễn quá 1023 của yyyy ( excess-1023 hoặc bias of 1023 ). Phần lẻ (fraction) dùng 52 bits để biểu diễn Tổng quát, số thực dấu chấm động được tính dựa theo (với Bias = 1023): Số thực dấu chấm động Biểu diễn số thực dấu chấm động Biểu diễn số thực dấu chấm động theo chuẩn IEEE 754 ( với độ chính xác kép ) 12 Ví dụ: Số -0.75 sẽ được biểu diễn trong máy tính như thế nào nếu dùng chuẩn IEEE 754 với độ chính xác kép -0.75 ten = -3/4 ten = -3/2 2 ten = -11 two /2 2 ten = 0.11 two Chuẩn hóa: 0.11 two = 1. 1 two x 2 -1 (phần exponent = -1 + 1023 = 1022 = 01111111110) Số thực dấu chấm động Biểu diễn số thực dấu chấm động Tại sao IEEE 754 không sử dụng biểu diễn dạng bù hai cho phần mũ mà dùng dạng bias-of-127 cho độ chính xác đơn và và bias-of-1023 cho độ chính xác kép? Ví dụ: giả sử dùng bù 2 để biểu diễn phần mũ cho 2 số sau: 1.0 two x 2 -1 13 1.0 two x 2 +1 Khi nhìn vào phần mũ của 1.0 two x 2 -1 thì nó lại giống như là số rất lớn (thực chất lại là nhỏ), còn trong khi nhìn vào phần mũ của 1.0 two x 2 +1 thì nó lại giống như là số nhỏ (thực chất lại là lớn) vì vậy IEEE 754 chọn cách biểu diễn dùng bias-of-127 cho độ chính xác đơn thay vì bù 2 Số thực dấu chấm động Biểu diễn số thực dấu chấm động dùng IEEE 754 14 IEEE 754 mã hóa số thực dấu chấm động Dãy biểu diễn số độ chính xác đơn có tầm trị từ: Đến số lớn nhất Số nhỏ nhất: 03/2017 Copyrights 2017 CE-UIT. All Rights Reserved. Số thực dấu chấm động Biểu diễn số thực dấu chấm động Các vấn đề cần lưu ý: Rõ ràng, trong một biểu diễn số thực dấu chấm động nếu - Tăng số bit chứa phần fraction thì tăng độ chính xác. Tăng kích thước phần exponent là tăng tầm trị biểu diễn. Vì vậy, khi thiết kế một biểu diễn/thể hiện cho số dấu chấm động (ví dụ không sử dụng IEEE 754) thì tùy vào mục đích sử dụng mà lựa chọn số giới hạn cho fraction và exponent sao cho phù hợp nhất. 15 03/2017 Copyrights 2017 CE-UIT. All Rights Reserved. Số thực dấu chấm động Biểu diễn số thực dấu chấm động Các vấn đề cần lưu ý: Số thực dấu chấm động dạng nhị phân (binary floating-point) dạng chuẩn 1.xxxxxxxxx two × 2 yyyy Số thực dấu chấm động dạng thập phân (decimal floating-point) dạng chuẩn: 1.xxxxxxxxx ten × 10 yyyy yyyy : exponent (phần mũ) xxxxxxxxx : fraction (tạm dịch là phần phân số/lẻ ) 1.xxxxxxxxx : significand (tạm dịch là phần trị) 16 03/2017 Copyrights 2017 CE-UIT. All Rights Reserved. Số thực dấu chấm động Phép toán cộng trên số thực dấu chấm động Ví dụ: Thực hiện cộng hai số thực dấu chấm động chuẩn trong hệ thập phân sau 9.999 ten x 10 1 + 1.610 ten x 10 -1 . Giả sử số thực dấu chấm động lưu trữ phần trị (significand) dùng 4 chữ số, phần số mũ (exponent) lưu trữ dùng 2 chữ số. 17 Bước 1. Điều chỉnh sao cho phần mũ của hai số hạng trở thành bằng nhau (Lấy số hạng có số mũ nhỏ hơn điều chỉnh theo số hạng có số mũ lớn hơn) 1.610 ten x 10 -1 = 0.01610 ten x 10 1 Vì significand chỉ cho phép dùng 4 chữ số, nên 0.01610 ten x 10 1 làm tròn thành 0.016 x 10 1 (quy tắc làm tròn tùy vào đề bài yêu cầu. Trong ví dụ này, làm tròn theo quy tắc nếu chữ số bên phải của phần bỏ đi lớn hơn hoặc bằng 5 thì chữ số bên trái nhất của phần còn lại tăng lên 1) 03/2017 Copyrights 2017 CE-UIT. All Rights Reserved. Số thực dấu chấm động Phép toán cộng trên số thực dấu chấm động 18 Bước 2. Thực hiện cộng phần significand của hai số hạng Tổng là 10.015 ten × 10 1 Bước 3. - Chuyển tổng về dạng chuẩn hóa: 10.015 ten × 10 1 =1.0015 × 10 2 - Kiểm tra phần mũ có bị tràn trên, tràn dưới ? => không tràn (Nếu tràn, phép toán sẽ tạo ra một ngoại lệ (exception) và dừng) Bước 4. Làm tròn tổng: vì significand chỉ cho phép dùng 4 chữ số, nên 1.0015 × 10 2 làm tròn thành 1.002 × 10 2 Lưu ý: Việc làm tròn trong một số trường hợp có thể làm tổng mất đi dạng chuẩn hóa. Vì vậy sau khi làm tròn, phải kiểm tra xem tổng có còn trong dạng chuẩn hóa hay không, nếu không, quay lại bước 3 03/2017 Copyrights 2017 CE-UIT. All Rights Reserved. Phép toán cộng trên số thực dấu chấm động 19 Giải thuật thực hiện phép cộng trên số thực dấu chấm động trong hệ nhị phân tương tự như cho số hệ thập phân Số thực dấu chấm động 03/2017 Copyrights 2017 CE-UIT. All Rights Reserved. Số thực dấu chấm động Phép toán cộng trên số thực dấu chấm động 20 Ví dụ: Cộng 2 số thực dấu chấm động trong hệ nhị phân cho 2 số thập phân sau: 0.5 10 và -0.4375 10 theo lưu đồ giải thuật. Giả sử phần significant dùng 4 bits lưu trữ, còn phần mũ lưu trữ như IEEE 754 độ chính xác đơn. Đáp án : 03/2017 Copyrights 2017 CE-UIT. All Rights Reserved. Số thực dấu chấm động 21 03/2017 Copyrights 2017 CE-UIT. All Rights Reserved. 22 Kiến trúc phần cứng phép nhân hai số floating-point: Chọn phần mũ lớn hơn Significand of the smaller number Significand of the larger number Shift n bits (n-different between exponents) 03/2017 Số thực dấu chấm động Phép nhân trên số thực dấu chấm động Ví dụ: Thực hiện phép nhân hai số thực dấu chấm động chuẩn trong hệ thập phân sau: (1.110 10 × 10 10 ) × (9.200 10 × 10 -5 ) Giả sử số thực dấu chấm động lưu trữ phần trị dùng 4 chữ số và phần mũ dùng 2 chữ số. 23 Đáp án : 03/2017 Copyrights 2017 CE-UIT. All Rights Reserved. Số thực dấu chấm động Phép nhân trên số thực dấu chấm động 24 Chú ý: kiểm tra số mũ có bị tràn trên, tràn dưới ? 03/2017 Số thực dấu chấm động Phép nhân trên số thực dấu chấm động 25 03/2017 Copyrights 2017 CE-UIT. All Rights Reserved. Số thực dấu chấm động Phép nhân trên số thực dấu chấm động Việc thực hiện phép nhân trên số thực dấu chấm động nhị phân cũng tương tự như ví dụ trên, nhưng lưu ý phần mũ khi được lưu theo định dạng IEEE 754 26 Phần mũ của tích khi lưu trữ : 137 ten + 122 ten = 259 ten Giá trị 259 ten đúng hay sai? Sai Giá trị đúng của tích trong lưu trữ phải là: ( 137 ten + 122 ten ) -127 ten = 132 ten Vì thực chất: - Số mũ của số thứ nhất là 10. Khi được lưu trữ theo IEEE 754, phần mũ lưu 10 + 127 = 137 - Số mũ của số thứ hai là -5. Khi được lưu trữ theo IEEE 754, phần mũ lưu -5 + 127 = 122 Số mũ của tích phải là 10 + (-5) = 5 Và nếu được lưu trữ theo IEEE 754, phần mũ của tích lưu 5 + 127 = 132 Vì vậy nếu lấy 137 + 122 thì 127 đã được cộng hai lần Ví dụ: Cần nhân hai số thực dấu chấm động đang được lưu trữ theo IEEE 754 độ chính xác đơn, biết 8 bit phần mũ của số thứ nhất trong lưu trữ có giá trị là 137 ten và 8 bit phần mũ của số thứ hai trong lưu trữ có giá trị là 122 ten . 03/2017 Copyrights 2017 CE-UIT. All Rights Reserved. Số thực dấu chấm động 27 Giải thuật nhân số thực dấu chấm động trên hệ nhị phân có 5 bước giống như là ví dụ phép nhân số trong hệ thập phân. Nhưng lưu ý: Bước 1 khi cộng hai exponent của hai số, nhớ trừ đi số bias Nếu IEEE 754 độ chính xác đơn: bias = 127 Nếu IEEE 754 độ chính xác kép: bias = 1023 Phép nhân trên số thực dấu chấm động 03/2017 Copyrights 2017 CE-UIT. All Rights Reserved. Số thực dấu chấm động Phép nhân trên số thực dấu chấm động Ví dụ: nhân số thực dấu chấm động trên hệ nhị phân cho 2 số sau: 0.5 10 và -0.4375 10 . Biết các số dấu chấm động dùng lưu trữ theo IEEE 754 độ chính xác đơn, nhưng phần significant chỉ cho phép 4 bits 28 03/2017 Copyrights 2017 CE-UIT. All Rights Reserved. Số thực dấu chấm động Phép nhân trên số thực dấu chấm động 29 03/2017 Số thực dấu chấm động Phép nhân trên số thực dấu chấm động 30 03/2017 Số thực dấu chấm động Sinh viên tìm hiểu: Phép chia với số floating-point trong MIPS Các lệnh làm việc với số floating-point trong MIPS Các lệnh liên quan đến số floating-point Phân biệt các lệnh: mult, multu, mul.s, mul.d div, divu, div.s, div.d 31 03/2017 Copyrights 2017 CE-UIT. All Rights Reserved. PHÉP TOÁN SỐ HỌC TRÊN MÁY TÍNH 32 Tổng kết: Hiểu cách biểu diễn số thực dấu chấm động theo IEEE 754 trong máy tính theo: Độ chính xác đơn Độ chính xác kép Hiểu cách máy tính thực hiện cộng, trừ, nhân chia trên số thực dấu chấm động Hiểu cách thiết kế một mạch cộng hai số thực dấu chấm động cơ bản 03/2017 Copyrights 2017 CE-UIT. All Rights Reserved. PHÉP TOÁN SỐ HỌC TRÊN MÁY TÍNH Lý thuyết: Đọc sách tham khảo Mục: 3.5 Sách: Computer Organization and Design: The Hardware/Software Interface , Patterson, D. A., and J. L. Hennessy, Morgan Kaufman, Revised Fourth Edition, 2011. Bài tập: file đính kèm 33 03/2017 Copyrights 2017 CE-UIT. All Rights Reserved.
File đính kèm:
 bai_giang_kien_truc_may_tinh_tuan_9_phep_toan_so_hoc_tren_ma.pptx
bai_giang_kien_truc_may_tinh_tuan_9_phep_toan_so_hoc_tren_ma.pptx

