Bài giảng Kiến trúc máy tính - Chương: Mạch logic
Là thiết bị điện tử hoạt động với 2 mức điện áp:
– Cao: thể hiện bằng giá trị luận lý (quy ước) là 1
– Thấp: thể hiện bằng giá trị luận lý (quy ước) là 0
• Được xây dựng từ những thành phần cơ bản là cổng luận lý (logic
gate)
– Cổng luận lý là thiết bị điện tử gồm 1 / nhiều tín hiệu đầu vào (input) -
1 tín hiệu đầu ra (output)
– output = F(input_1, input_2, , input_n)
– Tùy thuộc vào cách xử lý của hàm F sẽ tạo ra nhiều loại cổng luận lý
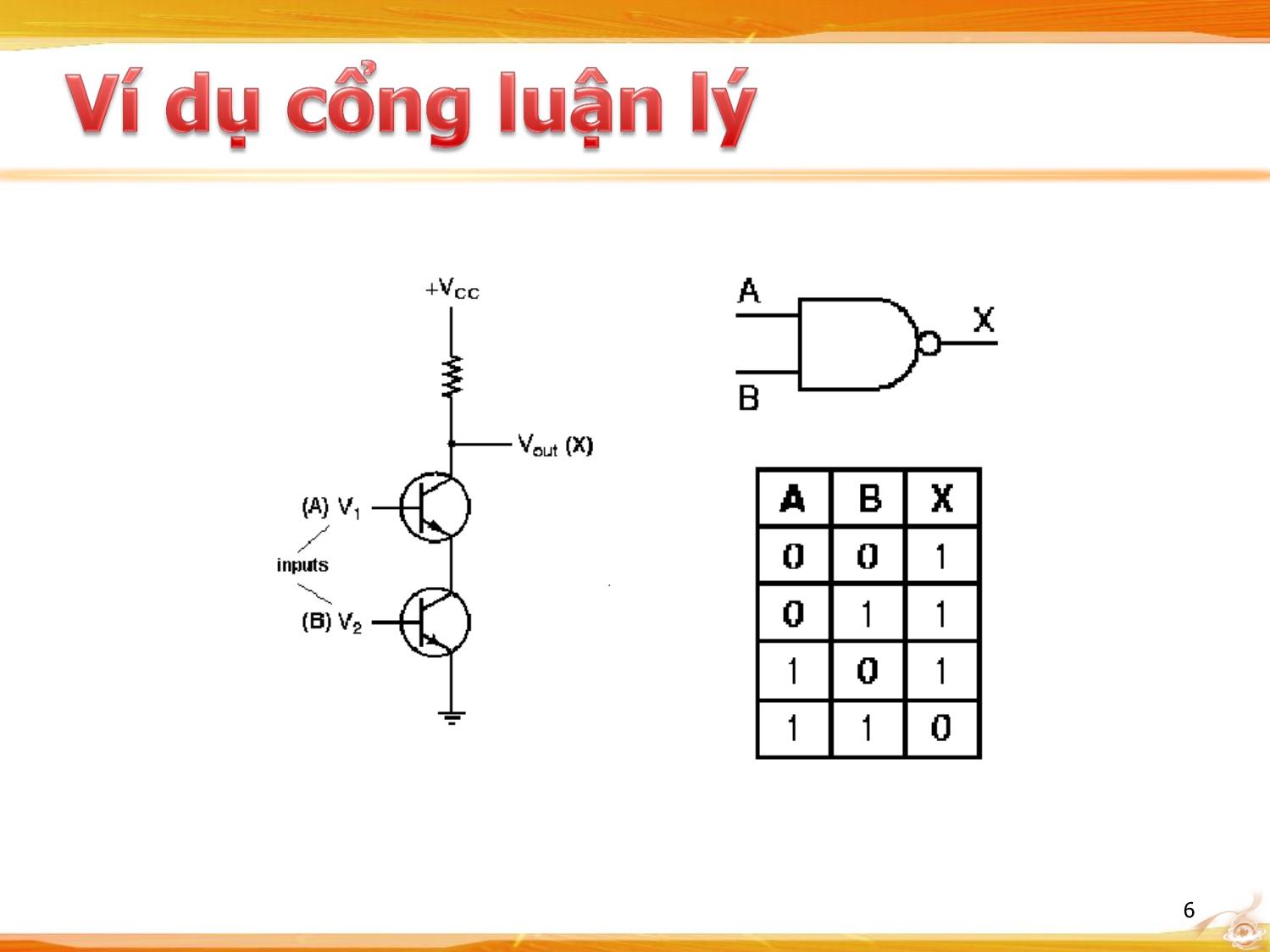
• Hiện nay linh kiện cơ bản để tạo ra mạch số là transistor

Trang 1

Trang 2

Trang 3
Trang 4
Trang 5
Trang 6
Trang 7
Trang 8

Trang 9

Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Kiến trúc máy tính - Chương: Mạch logic", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Kiến trúc máy tính - Chương: Mạch logic

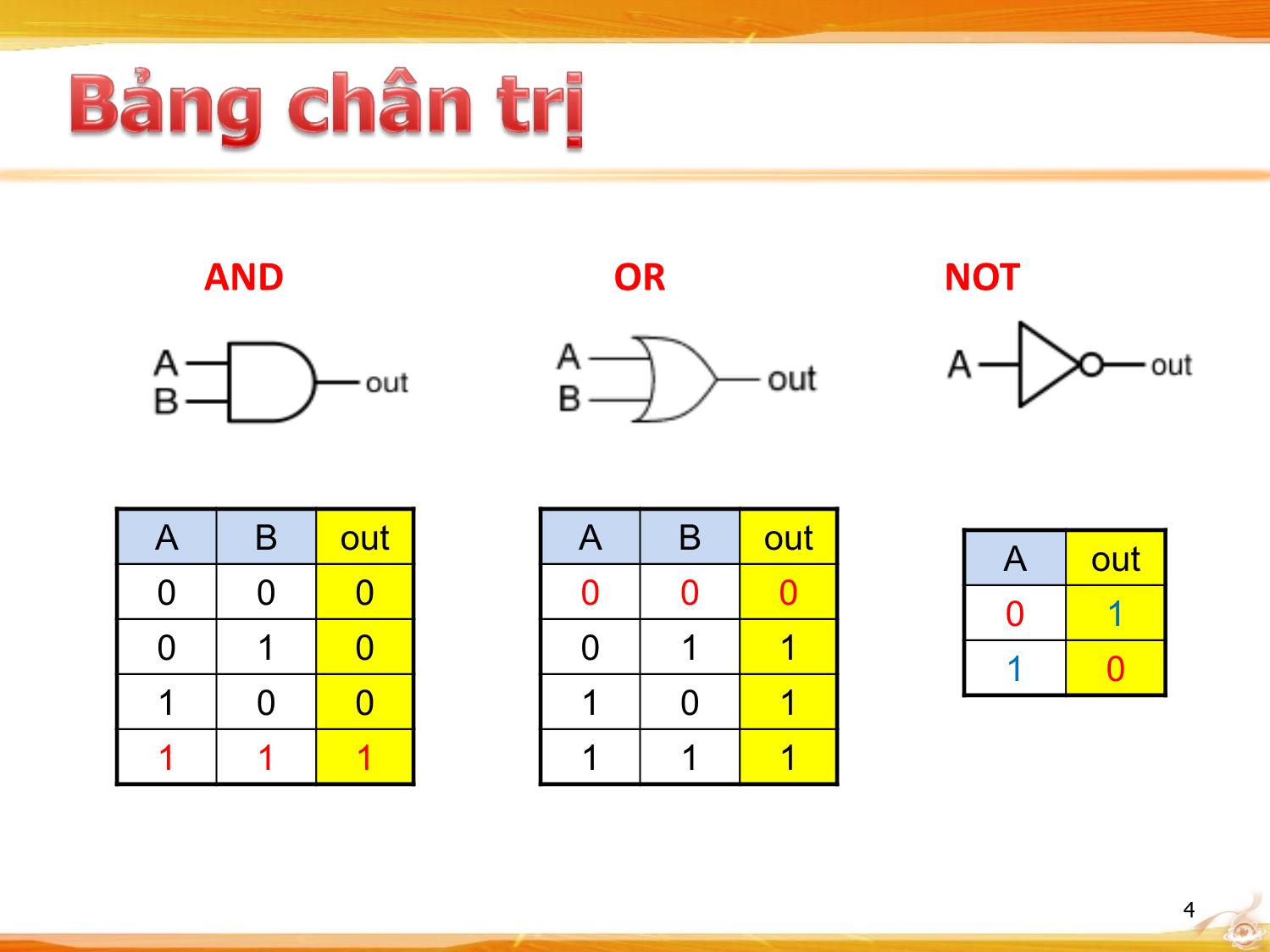
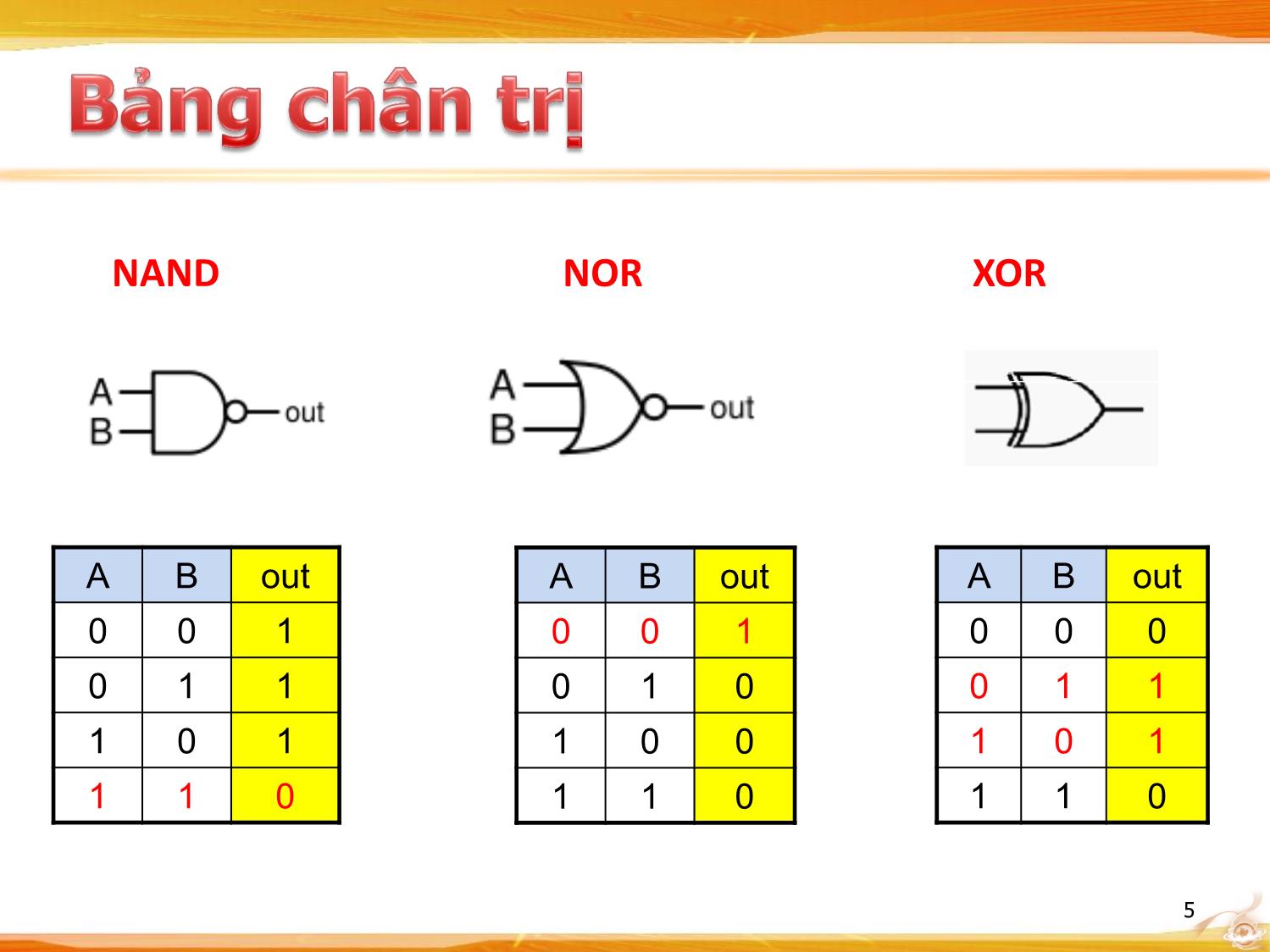
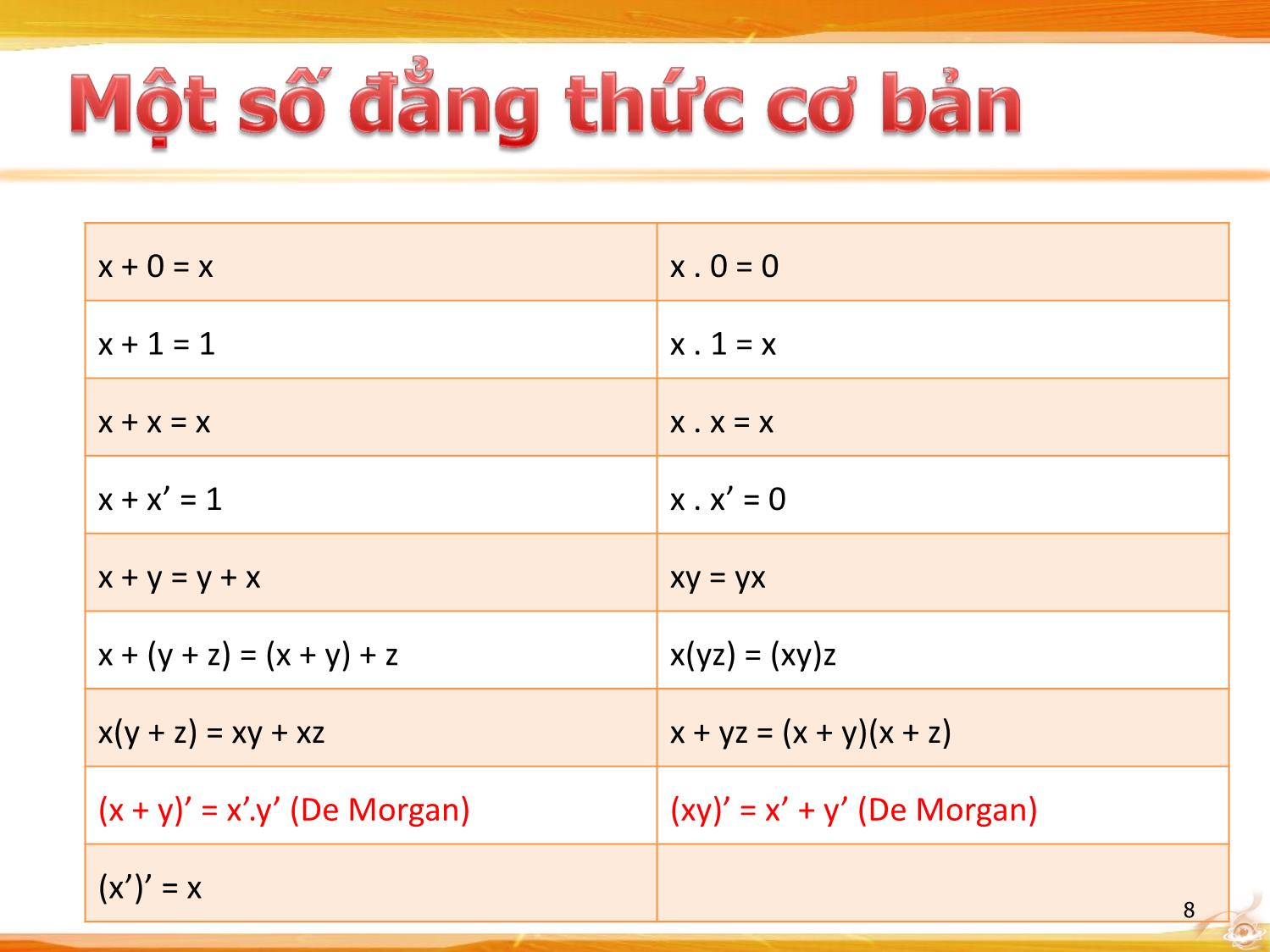
Môn học: Kiến trúc máy tính • Là thiết bị điện tử hoạt động với 2 mức điện áp: – Cao: thể hiện bằng giá trị luận lý (quy ước) là 1 – Thấp: thể hiện bằng giá trị luận lý (quy ước) là 0 • Được xây dựng từ những thành phần cơ bản là cổng luận lý (logic gate) – Cổng luận lý là thiết bị điện tử gồm 1 / nhiều tín hiệu đầu vào (input) - 1 tín hiệu đầu ra (output) – output = F(input_1, input_2, , input_n) – Tùy thuộc vào cách xử lý của hàm F sẽ tạo ra nhiều loại cổng luận lý • Hiện nay linh kiện cơ bản để tạo ra mạch số là transistor 2 Tên cổng Hình vẽ đại diện Hàm đại số Bun AND x.y hay xy OR x + y XOR x y NOT x’ hay x NAND (x .y)’ hay x.y NOR (x + y)’ hay x + y NXOR (x y)’ hay x y 3 AND OR NOT A B out A B out A out 0 0 0 0 0 0 0 1 0 1 0 0 1 1 1 0 1 0 0 1 0 1 1 1 1 1 1 1 4 NAND NOR XOR A B out A B out A B out 0 0 1 0 0 1 0 0 0 0 1 1 0 1 0 0 1 1 1 0 1 1 0 0 1 0 1 1 1 0 1 1 0 1 1 0 5 6 7 x + 0 = x x . 0 = 0 x + 1 = 1 x . 1 = x x + x = x x . x = x x + x’ = 1 x . x’ = 0 x + y = y + x xy = yx x + (y + z) = (x + y) + z x(yz) = (xy)z x(y + z) = xy + xz x + yz = (x + y)(x + z) (x + y)’ = x’.y’ (De Morgan) (xy)’ = x’ + y’ (De Morgan) (x’)’ = x 8 • Gồm n ngõ vào (input); m ngõ ra (output) – Mỗi ngõ ra là 1 hàm luận lý của các ngõ vào • Mạch tổ hợp không mang tính ghi nhớ: Ngõ ra chỉ phụ thuộc vào Ngõ vào hiện tại, không xét những giá trị trong quá khứ 9 • The 7400 chip, containing four NAND gate • The two additional pins supply power (+5 V) and connect the ground. 10 • Bằng ngôn ngữ • Bằng bảng chân trị – n input – m output – 2n hàng – (n + m) cột • Bằng công thức (hàm luận lý) • Bằng sơ đồ 11 • Thường trải qua 3 bước: – Lập bảng chân trị A B F 0 0 1 0 1 1 1 0 1 1 1 0 – Viết hàm luận lý F = (AB)’ – Vẽ sơ đồ mạch và thử nghiệm 12 • Giả sử đã có bảng chân trị cho mạch n đầu vào x1,,xn và 1 đầu ra f • Ta dễ dàng thiết lập công thức (hàm) logic theo thuật toán sau: – Ứng với mỗi hàng của bảng chân trị có đầu ra = 1 ta tạo thành 1 tích có dạng u1.u2un với: xi nếu xi = 1 ui = (xi)’ nếu xi = 0 – Cộng các tích tìm được lại thành tổng công thức của f 13 14 • Trường hợp số hàng có giá trị đầu ra = 1 nhiều hơn = 0, ta có thể đặt g = (f)’ • Viết công thức dạng SOP cho g • Lấy f = (g)’ = (f’)’ để có công thức dạng POS (Tích các tổng) của f 15 16 • Sau khi viết được hàm logic, ta có thể vẽ sơ đồ của mạch tổ hợp từ những cổng luận lý cơ bản – Ví dụ: f = xy + xz • Tuy nhiên ta có thể viết lại hàm logic sao cho sơ đồ mạch sử dụng ít cổng hơn – Ví dụ: f = xy + xz = x(y + z) • Cách đơn giản hoá hàm tổng quát? Một số cách phổ biến: – Dùng đại số Boole (Xem lại bảng 1 số đẳng thức cơ bản để áp dụng) – Dùng bản đồ Karnaugh (Cac-nô) 17 • Dùng các phép biến đổi đại số Boole để lược giản hàm logic • Khuyết điểm: – Không có cách làm tổng quát cho mọi bài toán – Không chắc kết quả cuối cùng đã tối giản chưa • Ví dụ: Đơn giản hoá các hàm sau – F(x,y,z) = xyz + x’yz + xy’z + xyz’ 18 • Mỗi tổ hợp biến trong bảng chân trị gọi là bộ trị (tạm hiểu là 1 dòng) Biểu diễn hàm có n biến thì sẽ cho ra tương ứng 2n bộ trị, với vị trí các bộ trị được đánh số từ 0 Thông tin trong bảng chân trị có thể cô đọng bằng cách: – Liệt kê vị trí các bộ trị (minterm) với giá trị đầu ra = 1 (SOP) – Liệt kê vị trí các bộ trị (maxterm) với giá trị đầu ra = 0 (POS) 19 • F(x,y,z) = m1 + m4 + m5+ m6 + m7 = Σ(1,4,5,6,7) • F(x,y,z) = M0M2M3 = Π(0,2,3) Vị trí x y z minterm maxterm F 0 0 0 0 m0 = x’y’z’ M0 = x + y + z 0 1 0 0 1 m1 = x’y’z M1 = x + y + z’ 1 2 0 1 0 m2 = x’yz’ M2 = x + y’ + z 0 3 0 1 1 m3 = x’yz M3 = x + y’ + z’ 0 4 1 0 0 m4 = xy’z’ M4 = x’ + y + z 1 5 1 0 1 m5 = xy’z M5 = x’ + y + z’ 1 6 1 1 0 m6 = xyz’ M6 = x’ + y’ + z 1 7 1 1 1 m7 = xyz M7 = x’ + y’ + z’ 1 20 B B 21 B BC A 0 1 A 00 01 11 10 0 0 1 0 0 1 3 2 A 1 2 3 A 1 4 5 7 6 C C CD AB 00 01 11 10 00 0 1 3 2 01 4 5 7 6 B 11 12 13 15 14 A 10 8 9 11 10 D • F(A, B, C) = Σ(1, 4, 5, 6, 7) B B BC BC A 00 01 11 10 A 00 01 11 10 0 0 1 0 0 0 1 == A 1 1 1 1 1 A 1 1 1 1 1 C C 22 • Bộ trị giữa 2 ô liền kề trong bản đồ chỉ khác nhau 1 biến – Biến đó bù 1 ô, không bù ở ô kế hoặc ngược lại Các ô đầu / cuối của các dòng / cột là các ô liền kề 4 ô nằm ở 4 góc bản đồ cũng coi là ô liền kề 23 • Hàm logic F biểu diễn bảng chân trị được đưa vào bản đồ bằng các trị 1 tương ứng • Các ô liền kề có giá trị 1 được gom thành nhóm sao cho mỗi nhóm sau khi gom có tổng số ô là luỹ thừa của 2 (2, 4, 8,) • Các nhóm có thể dùng chung ô có giá trị 1 để tạo thành nhóm lớn hơn. Cố gắng tạo những nhóm lớn nhất có thể • Nhóm 2/4/8 ô sẽ đơn giản bớt 1/2/3 biến trong số hạng • Mỗi nhóm biểu diễn 1 số hạng nhân (Product), Cộng (Sum – OR) các số hạng này ta sẽ được biểu thức tối giản của hàm logic F 24 • F(A, B, C) = Σ(3, 4, 6, 7) B B BC BC A 00 01 11 10 A 00 01 11 10 0 1 0 1 A 1 1 1 1 A 1 1 1 1 C C F(A, B, C) = BC + AC’ 25 • F(A, B, C) = Σ(0, 2, 4, 5, 6) B B BC BC A 00 01 11 10 A 00 01 11 10 0 1 1 0 1 1 A 1 1 1 1 A 1 1 1 1 C C F(A, B, C) = C’ + AB’ 26 • F(A, B, C, D) = Σ(0, 1, 2, 6, 8, 9, 10) C C CD CD AB 00 01 11 10 AB 00 01 11 10 00 1 1 1 00 1 1 1 01 1 01 1 B B 11 11 A A 10 1 1 1 10 1 1 1 D D F(A, B, C) = B’D’ + B’C’ + A’CD’ 27 • Đôi khi biểu diễn dạng tổng các tích (SOP) sẽ khó làm khi số bộ trị có đầu ra = 1 < số bộ trị có đầu ra = 0 Dùng phương pháp tích các tổng (POS) • Hoàn toàn giống phương pháp đơn giản hàm theo dạng SOP, chỉ khác ta nhóm các ô liền kề = 0 thay vì 1 Tìm được F’ F = (F’)’ 28 • F(A, B, C, D) = Σ(0, 1, 2, 5, 8, 9, 10) C C CD CD AB 00 01 11 10 AB 00 01 11 10 00 1 1 0 1 00 1 1 0 1 01 0 1 0 0 01 0 1 0 0 B B 11 0 0 0 0 11 0 0 0 0 A A 10 1 1 0 1 10 1 1 0 1 D D F’(A, B, C) = CD + BD’ + AB F = (F’)’ = (A’ + B’)(C’ + D’)(B’ + D) 29 • Trong 1 số trường hợp ta không cần quan tâm đến giá trị ngõ ra của 1 số bộ trị nào đó (1 hay 0 đều được) • Trong bản đồ ta sẽ ghi tương ứng những ô đó là x (gọi là giá trị tuỳ chọn /không cần) • x có thể dùng để gom nhóm với các ô liền kề nhằm đơn giản hàm • Lưu ý: Không được gom nhóm bao gồm toàn những ô có giá trị x 30 • F(A, B, C) = Σ(0, 2, 6) • d(A, B, C) = Σ(1, 3, 5) Vị trí A B C F 0 0 0 0 1 1 0 0 1 x 2 0 1 0 1 3 0 1 1 x 4 1 0 0 0 5 1 0 1 x 6 1 1 0 1 7 1 1 1 0 31 F(A, B, C) = Σ(0, 2, 6) d(A, B, C) = Σ(1, 3, 5) B B BC BC A 00 01 11 10 A 00 01 11 10 0 1 x x 1 0 1 x x 1 A 1 x 1 A 1 x 1 C C F(A, B, C) = A’ + BC’ 32 • Yêu cầu: Thiết kế mạch tổ hợp 3 ngõ vào, 1 ngõ ra, sao cho giá trị logic ở ngõ ra là giá trị nào chiếm đa số trong các ngõ vào 33 • Gọi các ngõ vào là x, y, z - ngõ ra là f f(x, y, z) = Σ(3, 5, 6, 7) 34 f(x, y, z) = Σ(3, 5, 6, 7) y y yz yz x 00 01 11 10 x 00 01 11 10 0 1 0 1 x 1 1 1 1 x 1 1 1 1 z z f(x, y, z) = xz + xy + yz = x.(y+z) + yz 35 36 • Mạch tính toán số học – Mạch cộng/ trừ – Mạch nhân • Mạch so sánh • Mạch dồn/ tách • Thiết kế ALU 37 • Mạch tổ hợp thực hiện phép cộng số học 3 bit • Gồm 3 ngõ vào (A, B: bit cần cộng – Ci: bit nhớ) và 2 ngõ ra (kết quả có thể từ 0 đến 3 với giá trị 2 và 3 cần 2 bit biểu diễn – S: ngõ tổng, C0: ngõ nhớ) A B Ci S C0 S = F(A, B, Ci) 0 0 0 0 0 = Σ(1, 2, 4, 7) 0 1 0 1 0 1 0 0 1 0 C0 = F(A, B, Ci) 1 1 0 0 1 = Σ(3, 5, 6, 7) 0 0 1 1 0 0 1 1 0 1 1 0 1 0 1 1 1 1 1 1 38 A A AB AB Ci 00 01 11 10 Ci 00 01 11 10 0 1 1 0 1 Ci 1 1 1 Ci 1 1 1 1 B B S = F(A, B, Ci) = Σ(1, 2, 4, 7) C0 = F(A, B, Ci) = Σ(3, 5, 6, 7) S = A’BCi’ + AB’Ci’ + A’B’Ci + ABCi C0 = AB + BCi + ACi S = A B Ci (Lưu ý: x y = x’y + xy’) 39 • Có 2n (hoặc ít hơn) ngõ vào, n ngõ ra • Quy định chỉ có duy nhất một ngõ vào mang giá trị = 1 tại một thời điểm • Nếu ngõ vào = 1 đó là ngõ thứ k thì các ngõ ra tạo thành số nhị phân có giá trị = k 40 • Ngõ vào: X0, X1, X2, X3 • Ngõ ra: Y0, Y1 Y0 = X1+ X3 Y1 = X2 + X3 41 • Các ngõ vào được xem như có độ ưu tiên • Giá trị ngõ ra phụ thuộc vào các ngõ vào có độ ưu tiên cao nhất • Ví dụ: Độ ưu tiên ngõ vào x3 > x2 > x1 > x0 y0 = (x2 + x0x1’).x3’ y1 = (x2 + x1).x3’ y2 = x3 42 y0 = (x2 + x0x1’).x3’ y1 = (x2 + x1).x3’ y2 = x3 43 • Có n ngõ vào, 2n (hoặc ít hơn) ngõ ra • Quy định chỉ có duy nhất một ngõ ra mang giá trị = 1 tại một thời điểm • Nếu các ngõ vào tạo thành số nhị phân có giá trị = k thì ngõ ra = 1 đó là ngõ thứ k 44 45 • Còn gọi là mạch chọn dữ liệu • Chọn n ngõ trong 2n ngõ vào để quyết định giá trị của duy nhất 1 ngõ ra • Mạch dồn 2n – 1 có 2n ngõ nhập, 1 ngõ xuất và n ngõ nhập chọn 46 47 48 49 • Chọn n ngõ trong 2n ngõ vào để quyết định giá trị của duy nhất 1 ngõ ra • Mạch DEMUX 1-2n có 1 ngõ nhập, 2n ngõ xuất và n ngõ nhập chọn 50 51 52 • F = (5X + 2Y) % 4 • Input: X (2 bit), Y (2 bit) • Output: F (2 bit) Có 4 ngõ vào, 2 ngõ ra (mỗi ngõ có 1 tín hiệu biểu diễn cho 1 bit) 53 54 55 56
File đính kèm:
 bai_giang_kien_truc_may_tinh_chuong_mach_logic.pdf
bai_giang_kien_truc_may_tinh_chuong_mach_logic.pdf

