Bài giảng Kiến trúc máy tính - Chương 3: Phép số học

 Computer Architecture
 Computer Science & Engineering
 Chương 3 
 Phép số học
 BK
TP.HCM
 Các phép số học
  Các phép tính trên số nguyên
  Cộng và Trừ
  Nhân và Chia
  Xử lý tràn
  Số thực với dấu chấm di động (Floating-
 Point)
  Cách biểu diễn và các phép tính 
BK
TP.HCM
4/5/2019 Khoa Khoa học & Kỹ thuật Máy tính 2
 Nhắc lại mạch số
 Môn học:
  Nhập môn điện toán (Năm I)
  Thiết kế hệ thống số
BK
TP.HCM
4/5/2019 Khoa Khoa học & Kỹ thuật Máy tính 3
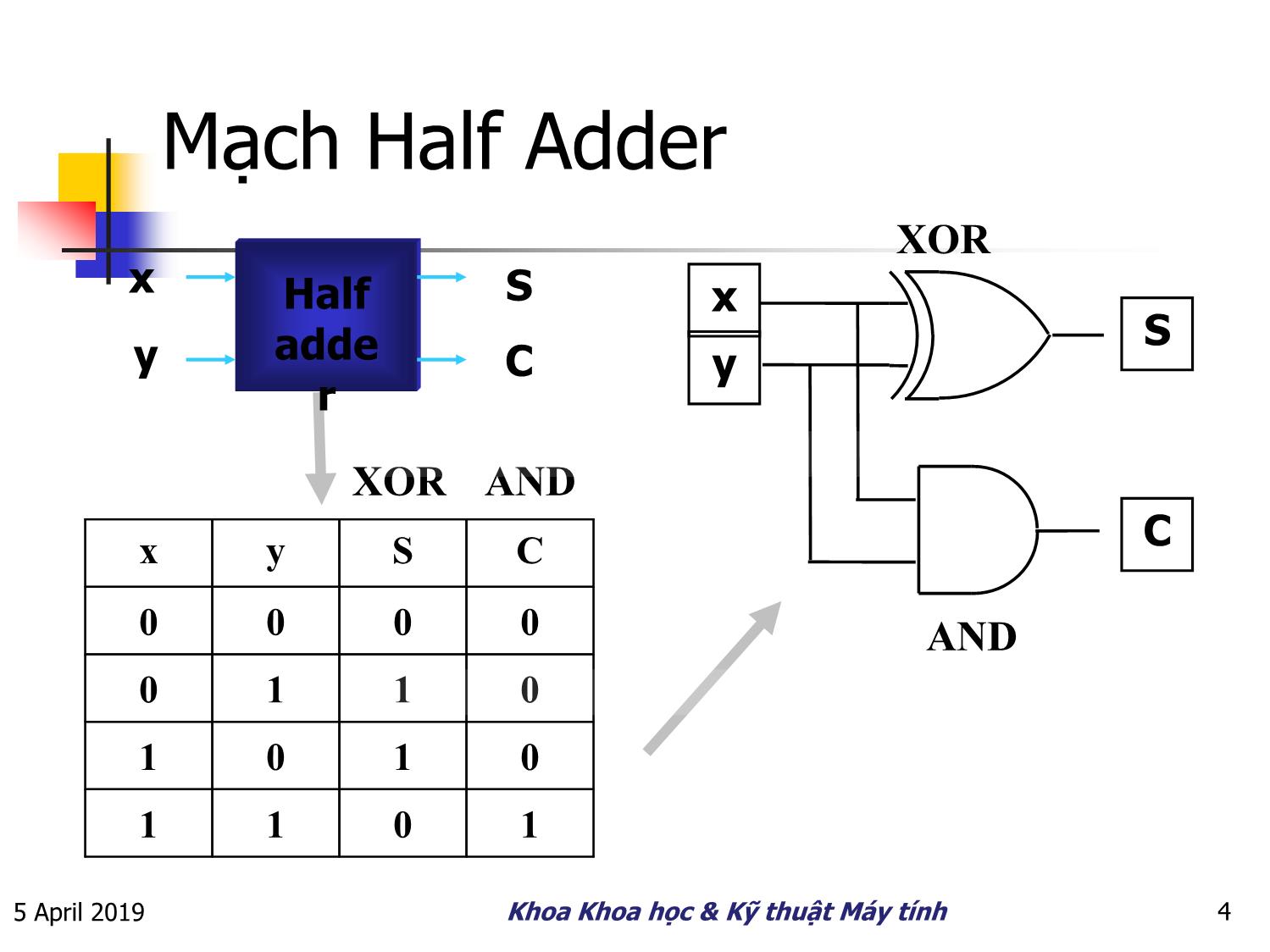
 Mạch Half Adder
 XOR
 x Half S x
 S
 y adde C y
 r
 XOR AND
 x y S C C
 0 0 0 0 AND
 0 1 1 0
 1 0 1 0
 1 1 0 1
5 April 2019 Khoa Khoa học & Kỹ thuật Máy tính 4
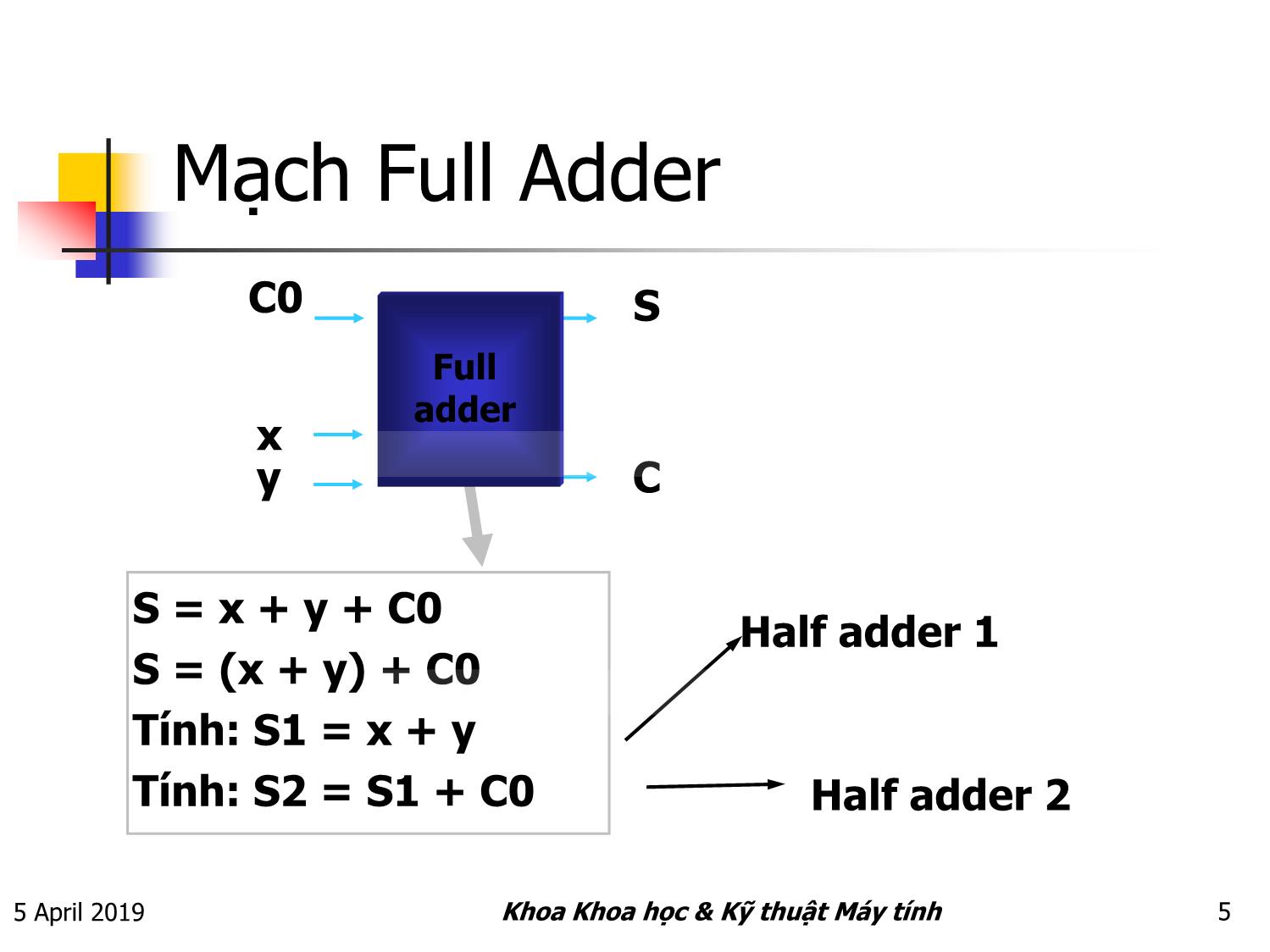
 Mạch Full Adder
 C0 S
 Full 
 adder
 x
 y C
 S = x + y + C0
 Half adder 1
 S = (x + y) + C0
 Tính: S1 = x + y
 Tính: S2 = S1 + C0 Half adder 2
5 April 2019 Khoa Khoa học & Kỹ thuật Máy tính 5
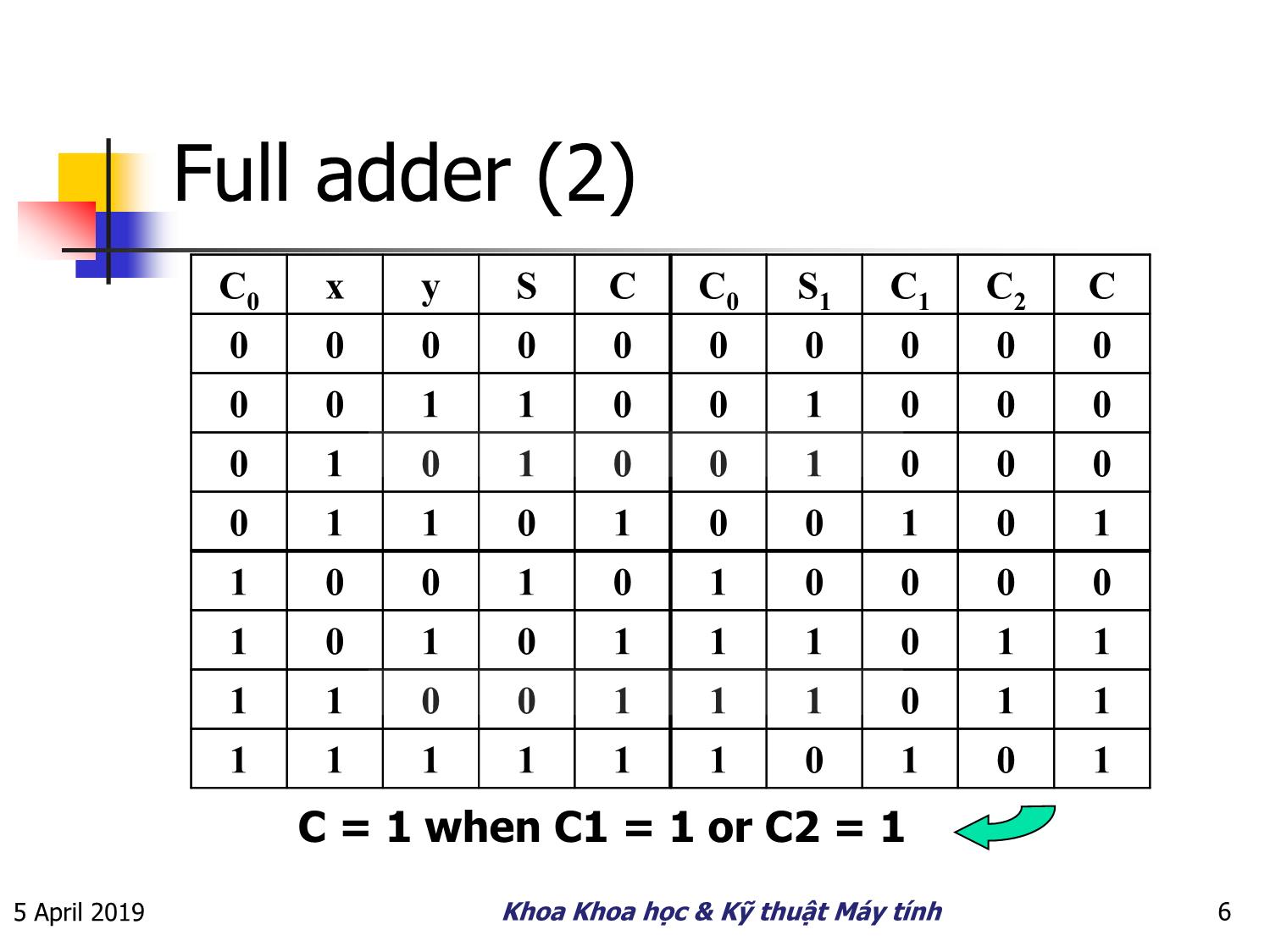
 Full adder (2)
 C0 x y S C C0 S1 C1 C2 C
 0 0 0 0 0 0 0 0 0 0
 0 0 1 1 0 0 1 0 0 0
 0 1 0 1 0 0 1 0 0 0
 0 1 1 0 1 0 0 1 0 1
 1 0 0 1 0 1 0 0 0 0
 1 0 1 0 1 1 1 0 1 1
 1 1 0 0 1 1 1 0 1 1
 1 1 1 1 1 1 0 1 0 1
 C = 1 when C1 = 1 or C2 = 1
5 April 2019 Khoa Khoa học & Kỹ thuật Máy tính 6
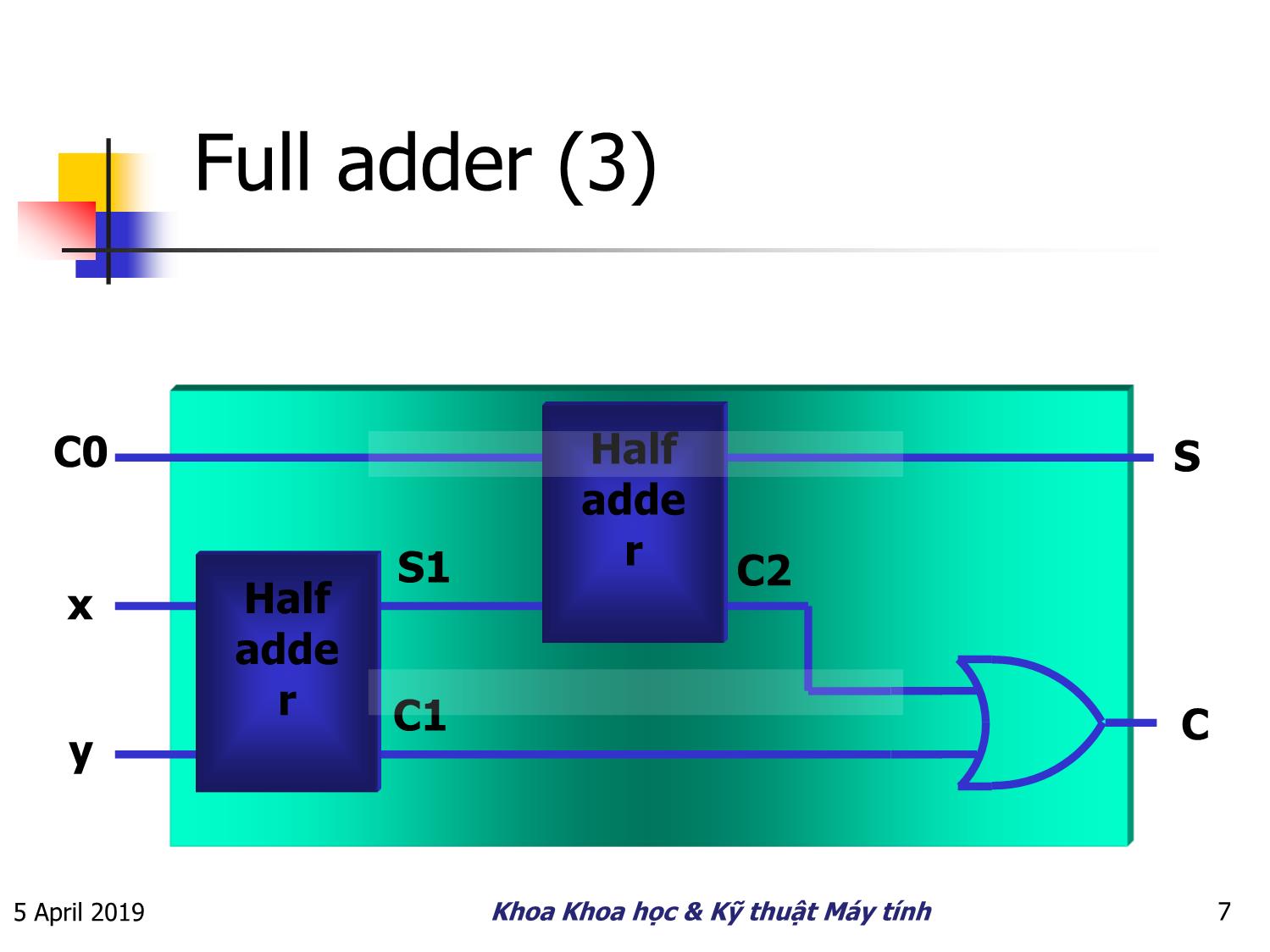
 Full adder (3)
 C0 Half S
 adde
 S1 r C2
 x Half 
 adde
 r
 C1 C
 y
5 April 2019 Khoa Khoa học & Kỹ thuật Máy tính 7
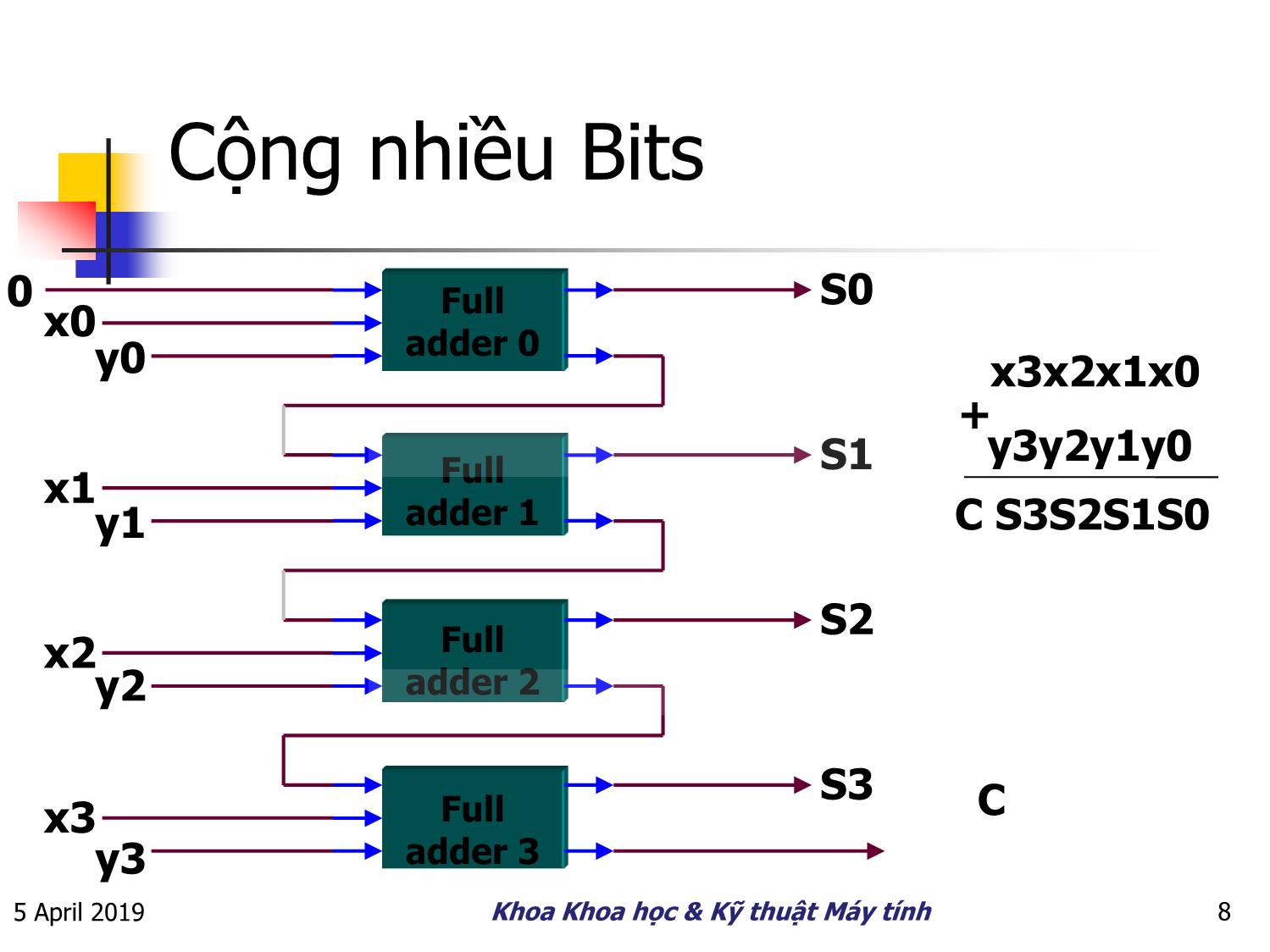
 Cộng nhiều Bits
0 S0
 x0 Full 
 adder 0
 y0 x3x2x1x0
 +
 S1 y3y2y1y0
 x1 Full 
 y1 adder 1 C S3S2S1S0
 S2
 x2 Full 
 y2 adder 2
 S3
 x3 Full C
 y3 adder 3
5 April 2019 Khoa Khoa học & Kỹ thuật Máy tính 8
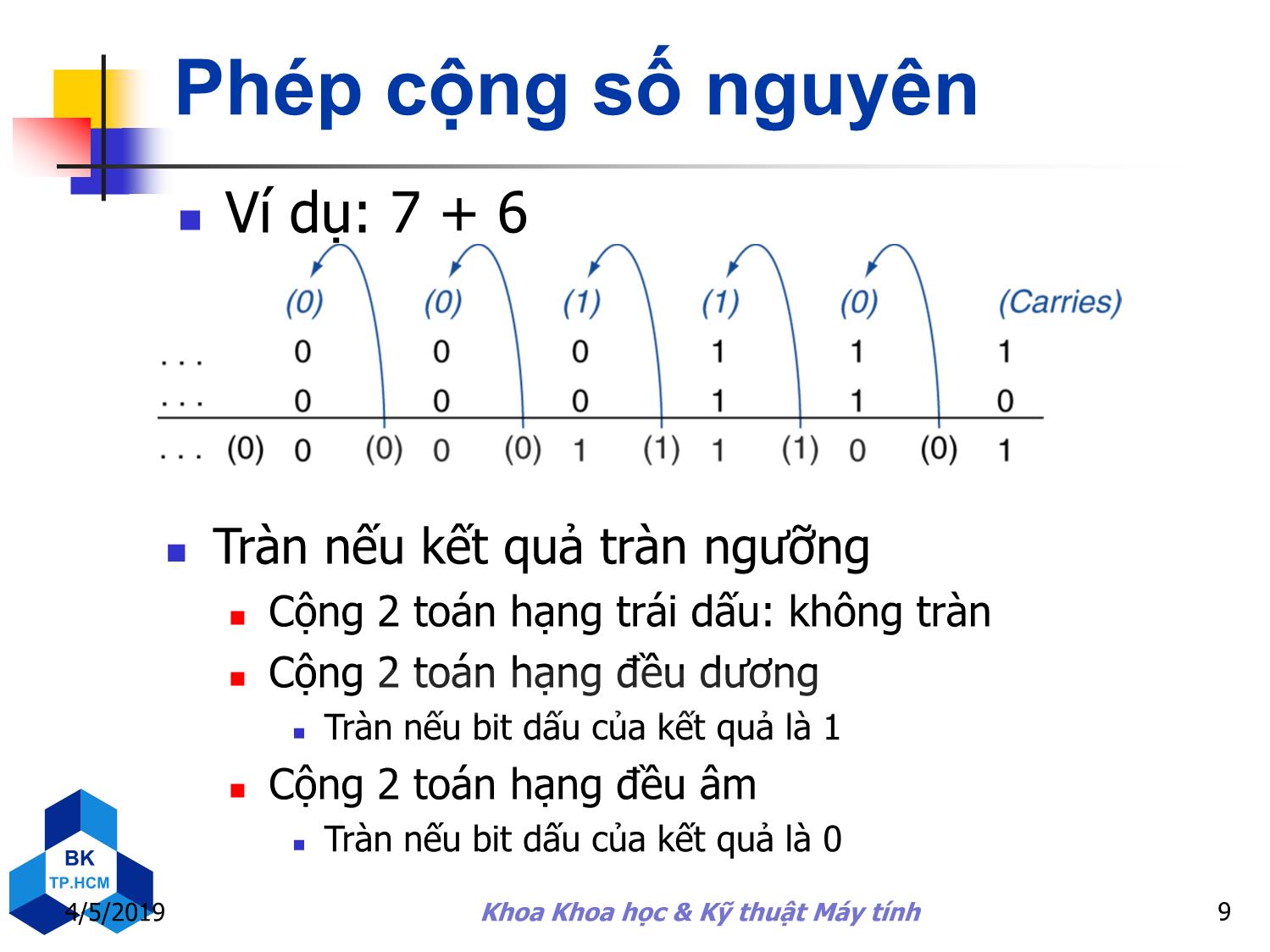
 Phép cộng số nguyên
  Ví dụ: 7 + 6
  Tràn nếu kết quả tràn ngưỡng
  Cộng 2 toán hạng trái dấu: không tràn
  Cộng 2 toán hạng đều dương
  Tràn nếu bit dấu của kết quả là 1
  Cộng 2 toán hạng đều âm
  Tràn nếu bit dấu của kết quả là 0
 BK
TP.HCM
 4/5/2019 Khoa Khoa học & Kỹ thuật Máy tính 9
 Phép trừ số nguyên
  Cộng số âm của toán hạng thứ 2
  Ví dụ: 7 – 6 = 7 + (–6)
 +7: 0000 0000  0000 0111
 –6: 1111 1111  1111 1010
 +1: 0000 0000  0000 0001
  Tràn nếu kết quả vượt ngưỡng
  Phép trừ 2 toán hạng cùng dấu, không bao giờ tràn
  Trừ 1 toán hạng âm với 1 toán hạng dương
  Tràn nếu bit dấu của kết quả là 0
  Trừ 1 toán hạng dương với 1 toán hạng âm
  Tràn nếu bit dấu của kết quả là 1
BK
TP.HCM
4/5/2019 Khoa Khoa học & Kỹ thuật Máy tính 10
 Xử lý tràn
  Một số ngôn ngữ (như C) không xử lý tràn
  Sử dụng lệnh MIPS: addu, addui, subu
  Các ngôn ngữ khác (như Ada, Fortran) yêu 
 cầu xử lý tràn bằng ngoại lệ
  Sử dụng lệnh MIPS: add, addi, sub
  Khi có tràn, bẫy bằng ngoại lệ & xử lý:
  Cất PC vào thanh ghi exception PC (EPC)
  Nhảy đến chương trìn xử lý tràn
  Dùng mfc0 khôi phục giá trị EPC value, trở về sau 
 khi xử lý tràn
BK
TP.HCM
4/5/2019 Khoa Khoa học & Kỹ thuật Máy tính 11
 Phép nhân
  Bắt đầu bằng phép nhân thuần túy
multiplicand
 1000
 multiplier × 1001
 1000
 0000 
 0000 
 1000 
 product 1001000
 Length of product is 
 the sum of operand 
 lengths
 BK
TP.HCM
 4/5/2019 Khoa Khoa học & Kỹ thuật Máy tính 12
 Phần cứng thực hiện nhân
 BK
TP.HCM
 4/5/2019 Khoa Khoa học & Kỹ thuật Máy tính 13
 Bộ nhân cải thiện
  Các bước song song: add/shift
  Một chu kỳ cho mỗi phép cộng (tích thành phần)
  Có thể chấp nhận khi tần xuất thấp
 BK
TP.HCM
 4/5/2019 Khoa Khoa học & Kỹ thuật Máy tính 14
 Bộ nhân nhanh
  Sử dụng nhiều bộ cộng cùng lúc
  Cost/performance tradeoff
  Có thể thực hiện theo cơ chế ống
 
BK Nhiều tác vụ nhân thực hiện cùng lúc
TP.HCM
4/5/2019 Khoa Khoa học & Kỹ thuật Máy tính 15
 Lệnh nhân trong MIPS
  Kết quả sẽ là 64-bit, chứa trong 2 thanh ghi 
 32-bit
  HI: chứa 32-bit cao
  LO: chứa 32-bit thấp
  Lệnh nhân
  mult rs, rt / multu rs, rt
  64-bit kết quả chứa trong HI/LO
  mfhi rd / mflo rd
  Chuyển từ HI/LO vào rd
  Có thể kiểm tra giá trị HI xem kết quả phép nhân có 
 tràn?
  mul rd, rs, rt
  32 bits thấp của kết quả phép nhân –> rd
 BK
TP.HCM
 4/5/2019 Khoa Khoa học & Kỹ thuật Máy tính 16
 Phép chia
 Divisor
 (số chia)
 Quotient  Kiểm tra chia 0 báo lỗi
 (thương số)
  Long division approach
 Dividend  If divisor ≤ dividend bits
 (số bị chia)
 1001  1 bit in quotient, subtract
 1001010/1000  Otherwise
 -1000  0 bit in quotient, bring down 
 10 next dividend bit
 101  Restoring division
 1010  Do the subtract, and if remainder 
 -1000 goes < 0, add divisor back
 Remainder 10
 (số dư)  Signed division
  Divide using absolute values
 Toán hạng n-bit cho kết quả n-bit
  Adjust sign of quotient and 
 thương số và số dư
 remainder as required
 BK
TP.HCM
 4/5/2019 Khoa Khoa học & Kỹ thuật Máy tính 17
 Phần cứng thực hiện chia
 Initially divisor 
 in left half
 Initially dividend
 BK
TP.HCM
 4/5/2019 Khoa Khoa học & Kỹ thuật Máy tính 18
 Bộ chia cải thiện
  Một chu kỳ cho mỗi phép trừ thành phần
  Tương tự rất nhiều với bộ nhân
  Có thể dùng cùng một phần cứng cho cả 2
 BK
TP.HCM
 4/5/2019 Khoa Khoa học & Kỹ thuật Máy tính 19
 Bộ chia nhanh
  Không thể thực hiện song song như 
 trong bộ nhân
  Dấu trong mỗi phép trừ thành phần là điều 
 kiện
  Có thể tạo bộ chia nhanh (e.g. SRT 
 devision)
BK
TP.HCM
4/5/2019 Khoa Khoa học & Kỹ thuật Máy tính 20
 Lệnh chia trong MIPS
  Thanh ghi HI/LO chứa kết quả phép 
 chia
  HI: 32-bit số dư (remainder)
  LO: 32-bit (kết quả) quotient
  Lệnh trong MIP
  div rs, rt / divu rs, rt
  Không kiểm tra tràn hoặc lỗi /0
  Nếu có yêu cầu, phần mềm phải tự thực hiện
  Sử dụng lệnh mfhi, mflo để lấy kết quả
 BK
TP.HCM
 4/5/2019 Khoa Khoa học & Kỹ thuật Máy tính 21
 Dấu chấm di động (Floating Point)
  Biểu diễn các số khác số nguyên (số thực)
  Bao gồm cả số rất nhỏ lẫn số rất lớn
  Giống như biểu diễn số trong khoa học
 56
  –2.34 × 10
 –4
  +0.002 × 10
 9
  +987.02 × 10
  Kiểu nhị phân
 yyyy
  1.xxxxxxx2 2
  Kiểu float và double trong ngôn ngữ C
BK
TP.HCM
4/5/2019 Khoa Khoa học & Kỹ thuật Máy tính 22
 Chuẩn của hệ thống số chấm di động
  Định chuẩn bởi Tổ chức IEEE(754-1985)
  Được phát triển nhằm đáp ứng tiêu
 chuẩn trình bày thống nhất
  Dễ sử dụng và chuyển đổi giữa các bộ mã
 trong khoa học
  Hiện nay trở thành thông dụng
  Tồn tại 2 cách biểu diễn
  Chính xác đơn(32-bit)
 
BK Chính xác kép (64-bit)
TP.HCM
4/5/2019 Khoa Khoa học & Kỹ thuật Máy tính 23
 Dạng định chuẩn theo IEEE
  S: bit dấu (0 (+) , 1 (-))
  Normalize significand: 1.0 ≤ |significand| < 2.0
  Luôn có 1 bit trước dấu chấm, nên bit này thường ẩn
  Significand is Fraction with the “1.” restored
  Exponent: excess representation: actual exponent + Bias
  Ensures exponent is unsigned
  Single: Bias = 127; Double: Bias = 1203
 BK
TP.HCM
 4/5/2019 Khoa Khoa học & Kỹ thuật Máy tính 24
 Tầm giá trị với độ chính xác đơn
  Giá trị (Exponents) 00000000 và 11111111 : dự trữ
  Giá trị nhỏ nhất
  Số mũ: 00000001
 số mũ thực chất sẽ là = 1 – 127 = –126
  Fraction: 00000 significand = 1.0
 –126 –38
  ±1.0 × 2 ≈ ±1.2 × 10
  Giá trị lớn nhất:
  Số mũ: 11111110
 số mũ thực tế sẽ là = 254 – 127 = +127
  Fraction: 11111 significand ≈ 2.0
 +127 +38
  ±2.0 × 2 ≈ ±3.4 × 10
 BK
TP.HCM
 4/5/2019 Khoa Khoa học & Kỹ thuật Máy tính 25
 Mức độ chính xác
  Mang tính tương đối
  Xác định bởi các bit fraction
 –23
  Đơn: khoảng 2
  Tương đương với 23 × log102 ≈ 23 × 0.3 ≈ 6:
 chính xác đến 6 số (hệ thập phân)
 –52
  Kép: khoảng 2
  Tương đương với 52 × log102 ≈ 52 × 0.3 ≈ 16:
 chính xác đến 16 số (hệ thập phân)
BK
TP.HCM
4/5/2019 Khoa Khoa học & Kỹ thuật Máy tính 26
 Ví dụ: Dấu chấm di động
  Biểu diễn số thực thập phân: –0.75
 1 –1
  –0.75 = (–1) × 1.12 × 2
  S = 1
  Fraction = 1000002
  Exponent = –1 + Bias
  Đơn: –1 + 127 = 126 = 011111102
  Kép: –1 + 1023 = 1022 = 011111111102
  Single: 101111110100000
  Double: 101111111110100000
BK
TP.HCM
4/5/2019 Khoa Khoa học & Kỹ thuật Máy tính 27
 Ví dụ: (tt.)
  Cho biết số thực thập phân của một số 
 biểu diễn bằng dấu chấm di động (đơn) 
 sau:
 1100000010100000
  S = 1
  Fraction = 01000002
  Fxponent = 100000012 = 129
 1 (129 – 127)
  x = (–1) × (1 + 012) × 2
 = (–1) × 1.25 × 22
BK = –5.0
TP.HCM
4/5/2019 Khoa Khoa học & Kỹ thuật Máy tính 28
 Số vô hạn (Infinities) và
 Số không hợp lệ (NaNs)
  Exponent = 111...1, Fraction = 000...0
  ±Infinity
  Dùng để kiểm tra kết quả của phép tính
  Exponent = 111...1, Fraction ≠ 000...0
  Not-a-Number (NaN)
  Số không hợp lệ
  Ví dụ: chia cho zero: 0.0 / 0.0
  Dùng để kiểm tra kết quả của phép tính
 BK
TP.HCM
 4/5/2019 Khoa Khoa học & Kỹ thuật Máy tính 29
 Phép cộng
  Giả sử có phép cộng 2 số thập phân (4 ký số)
 1 –1
  9.999 × 10 + 1.610 × 10
  1. Điều chỉnh dấu chấm
  Dời số mũ của số nhỏ hơn cho đồng số mũ
 1 1
  9.999 × 10 + 0.016 × 10
  2. Cộng hệ số
 1 1 1
  9.999 × 10 + 0.016 × 10 = 10.015 × 10
  3. Chuẩn hóa kết quả & kiểm tra ngưỡng
 2
  1.0015 × 10
  4. Làm tròn và điều chỉnh nếu cần thiết
 2
  1.002 × 10
 BK
TP.HCM
 4/5/2019 Khoa Khoa học & Kỹ thuật Máy tính 30
 Cộng nhị phân
  Giả sử cộng 2 số nhị phân (4 ký số):
 –1 –2
  1.0002 × 2 + –1.1102 × 2 (0.5 + –0.4375)
  1. Điều chỉnh dấu chấm
  Dời số mũ của số nhỏ hơn cho đồng số mũ
 –1 –1
  1.0002 × 2 + –0.1112 × 2
  2. Cộng hệ số
 –1 – –1
  1.0002 × 2 + –0.1112 × 2 1 = 0.0012 × 2
  3. Chuẩn hóa kết quả & kiểm tra ngưỡng
 –4
  1.0002 × 2 , (nằm trong ngưỡng cho phép)
  4. Làm tròn và điều chỉnh nếu cần thiết 
 –4
  1.000 × 2 (không cần điều chỉnh) = 0.0625
BK 2
TP.HCM
4/5/2019 Khoa Khoa học & Kỹ thuật Máy tính 31
 Phần cứng bộ cộng (FP)
  Phức tạp hơn rất nhiều so với bộ cộng số 
 nguyên
  Nếu thực hiện trong 1 chu kỳ đồng hồ - 
 Chu kỳ quá dài
  Dài hơn nhiều so với các phép cộng số nguyên
  Kéo dài thời gian xung đồng hồ ảnh hưởng đến 
 các lệnh khác
  Bộ cộng (FP) thường kéo dài nhiều chu kỳ
  Có thể cải thiện bằng cơ chế ống
 BK
TP.HCM
 4/5/2019 Khoa Khoa học & Kỹ thuật Máy tính 32
 Phần cứng bộ cộng (FP)
 Bước 1
 Bước 2
 Bước 3
 Bước 4
 BK
TP.HCM
 4/5/2019 Khoa Khoa học & Kỹ thuật Máy tính 33
 Phép nhân thập phân
  Giả sử nhân 2 số thập phân (4 ký số)
 10 –5
  1.110 × 10 × 9.200 × 10
  1. Cộng số mũ
  Nếu dùng số mũ biased, trừ biased vào tổng
  Số mũ mới là = 10 + –5 = 5
  2. Nhân hệ số
 5
  1.110 × 9.200 = 10.212 10.212 × 10
  3. Chuẩn hóa kết quả & kiểm tra ngưỡng
 6
  1.0212 × 10
  4. Làm tròn và điều chỉnh nếu cần thiết
  5. Xác định dấu của kết quả
 6
  +1.021 × 10
 BK
TP.HCM
 4/5/2019 Khoa Khoa học & Kỹ thuật Máy tính 34
 Phép nhân nhị phân (FP)
  Giả sử nhân 2 số thập phân (4 ký số)
 –1 –2
  1.0002 × 2 × –1.1102 × 2 (0.5 × –0.4375)
  1. Cộng số mũ
  Unbiased: –1 + –2 = –3
  Biased: (–1 + 127) + (–2 + 127) = –3 + 254 – 127 = –3 + 
 127
  2. Nhân hệ số
 –3
  1.0002 × 1.1102 = 1.1102 1.1102 × 2
  3. Chuẩn hóa kết quả & kiểm tra ngưỡng
 –3
  1.1102 × 2 (không đổi: nằm trong ngưỡng cho phép)
  4. Làm tròn và điều chỉnh nếu cần thiết
 –3
  1.1102 × 2 (no change)
  5. Xác định dấu: (+) × (–) (-)
 –3
 BK  –1.1102 × 2 = –0.21875
TP.HCM
 4/5/2019 Khoa Khoa học & Kỹ thuật Máy tính) 35
 Phần cứng Bộ số học (FP)
  Bộ nhân (FP) và Bộ cộng (FP) có độ 
 phức tạp như nhau
  Chỉ khác nhau cho phép tính hệ số
  Phần cứng Bộ số học thường thực hiện 
 các tác vụ sau:
  Cộng, Trừ, Nhân, Chia, Căn, Nghịch đảo
  Chuyển đổi FP integer
  Các tác vụ này thường kéo dài trong 
 nhiều chu kỳ xung đồng hồ
BK  Cải thiện bằng cơ chế đường ống
TP.HCM
4/5/2019 Khoa Khoa học & Kỹ thuật Máy tính 36
 Lệnh FP trong MIPS
  Phần cứng bộ FP là một coprocessor
  Mở rộng kiến trúc tập lệnh
  Có các thanh ghi FP riêng
  32 thanh ghi (đơn): $f0, $f1,  $f31
  Chính xác kép bằng cách ghép: $f0/$f1, $f2/$f3, ..
  Phiên bản 2 của MIPs ISA hỗ trợ 32 × 64-bit FP reg’s
  Các lệnh FP chỉ thực hiện trên các thanh ghi FP
  Chương trình thường không thực hiện các phép số 
 nguyên trên dữ liệu FP hoặc ngược lại
  Thanh ghi riêng không làm phức tạp thêm code
  Các lệnh FP load và store
  lwc1, ldc1, swc1, sdc1
  Ví dụ: ldc1 $f8, 32($sp)
BK
TP.HCM
4/5/2019 Khoa Khoa học & Kỹ thuật Máy tính 37
 Lệnh FP trong MIPS
  Phép tính số học (đơn)
  add.s, sub.s, mul.s, div.s
  Ví dụ: add.s $f0, $f1, $f6
  Phép tính số học (kép)
  add.d, sub.d, mul.d, div.d
  Ví dụ: mul.d $f4, $f4, $f6
  Lệnh so sánh (đơn/kép)
  c.xx.s, c.xx.d (xx is eq, lt, le, )
  Gán hoặc xóa bit điều kiện code
  e.g. c.lt.s $f3, $f4
  Rẽ nhánh theo điều kiện
  bc1t, bc1f
  Ví dụ: bc1t TargetLabel
BK
TP.HCM
4/5/2019 Khoa Khoa học & Kỹ thuật Máy tính 38
 Ví dụ: Chuyển °F sang °C
  C code:
 float f2c (float fahr) {
 return ((5.0/9.0)*(fahr - 32.0));
 }
  fahr chứa trong $f12, kết quả trong $f0, hằng số 
 trong bộ nhớ toàn cục
  Biên dịch thành MIPS code:
 f2c: lwc1 $f16, const5($gp)
 lwc2 $f18, const9($gp)
 div.s $f16, $f16, $f18
 lwc1 $f18, const32($gp)
 sub.s $f18, $f12, $f18
 mul.s $f0, $f16, $f18
BK jr $ra
TP.HCM
4/5/2019 Khoa Khoa học & Kỹ thuật Máy tính 39
 Ví dụ: Nhân Ma trận
  X = X + Y Z
  Tất cả đều là ma trận 32 32, các phần tử của ma trận 64-bit 
 (chính xác kép)
  C code:
 void mm (double x[][],
 double y[][], double z[][]) {
 int i, j, k;
 for (i = 0; i! = 32; i = i + 1)
 for (j = 0; j! = 32; j = j + 1)
 for (k = 0; k! = 32; k = k + 1)
 x[i][j] = x[i][j]
 + y[i][k] * z[k][j];
 }
  Địa chỉ của x, y, z chứa trong $a0, $a1, $a2, và 
 i, j, k trong $s0, $s1, $s2
 BK
TP.HCM
 4/5/2019 Khoa Khoa học & Kỹ thuật Máy tính 40
 Ví dụ: Nhân Ma trận (tt.)
 BK
TP.HCM
 4/5/2019 Khoa Khoa học & Kỹ thuật Máy tính 41
 Ví dụ: Nhân Ma trận (tt.)
 BK
TP.HCM
 4/5/2019 Khoa Khoa học & Kỹ thuật Máy tính 42
 Kết luận
  ISAs hỗ trợ phép số học
  Số nguyên có dấu và không dấu
  Floating-point approximation to reals
  Bounded range and precision
  Operations can overflow and underflow
  MIPS ISA
  Core instructions: 54 most frequently used
  100% of SPECINT, 97% of SPECFP
  Other instructions: less frequent
 BK
TP.HCM
 4/5/2019 Khoa Khoa học & Kỹ thuật Máy tính 43