Bài giảng Kiến trúc máy tính - Chương 2: Cơ bản về logic số - Nguyễn Kim Khánh
2.1. Các hệ đếm cơ bản
n Hệ thập phân (Decimal System)
à con người sử dụng
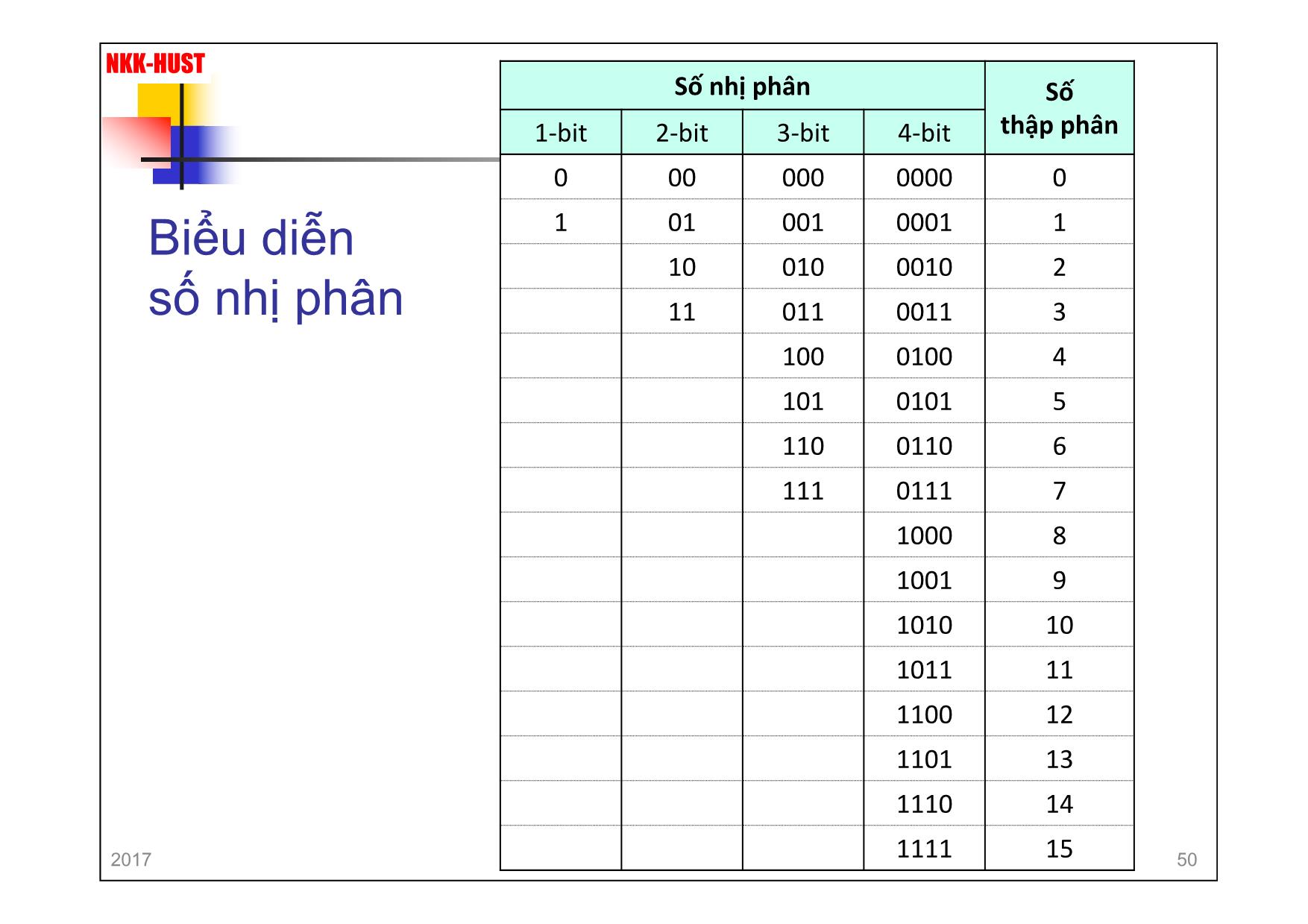
n Hệ nhị phân (Binary System)
à máy tính sử dụng
n Hệ mười sáu (Hexadecimal System)
à dùng để viết gọn cho số nhị phân

Trang 1

Trang 2

Trang 3

Trang 4

Trang 5

Trang 6

Trang 7

Trang 8
Trang 9

Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Kiến trúc máy tính - Chương 2: Cơ bản về logic số - Nguyễn Kim Khánh", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Kiến trúc máy tính - Chương 2: Cơ bản về logic số - Nguyễn Kim Khánh

B16 8-bit adder A15 C7 B15 S15 S8 A8 B8 8-bit adder A7 Cin B7 S7 S0 A0 B0 8-bit adder Figure 11.21 Construction of a 32-Bit Adder Using 8-Bit Adders 386 CHAPTER 11 / DIGITAL LOGIC 0 0 1 1 +0 +1 +0 +1 0 1 1 10 However, addition can still be dealt with in Boolean terms. In Table 11.9a, we show the logic for adding two input bits to produce a 1-bit sum and a carry bit. This truth table could easily be implemented in digital logic. However, we are not interested in performing addition on just a single pair of bits. Rather, we wish to add two n-bit numbers. This can be done by putting together a set of adders so that the carry from one adder is provided as input to the next. A 4-bit adder is depicted in Figure 11.19. For a multiple-bit adder to work, each of the single-bit adders must have three inputs, including the carry from the next-lower-order adder. The revised truth table appears in Table 11.9b. The two outputs can be expressed: Sum = A BC + ABC + ABC + ABC Carry = AB + AC + BC Figure 11.20 is an implementation using AND, OR, and NOT gates. A3 C3 S3 Cin B3 A2 C2 S2 Cin B2 A1 C1 S1 Cin B1 A0 C0 S0 Cin 0 B0 Overflow signal Figure 11.19 4-Bit Adder Table 11.9 Binary Addition Truth Tables (a) Single-Bit Addition A B Sum Carry 0 0 0 0 0 1 1 0 1 0 1 0 1 1 0 1 (b) Addition with Carry Input Cin A B Sum Cout 0 0 0 0 0 0 0 1 1 0 0 1 0 1 0 0 1 1 0 1 1 0 0 1 0 1 0 1 0 1 1 1 0 0 1 1 1 1 1 1 2017 Kiến trúc máy tính 81 NKK-HUST 2.5. Mạch dãy n Mạch dãy là mạch logic trong đó đầu ra phụ thuộc giá trị đầu vào ở thời điểm hiện tại và đầu vào ở thời điểm quá khứ n Là mạch có nhớ, được thực hiện bằng phần tử nhớ (Latch, Flip-Flop) và có thể kết hợp với các cổng logic 2017 Kiến trúc máy tính 82 NKK-HUST Các Flip-Flop cơ bản 392 CHAPTER 11 / DIGITAL LOGIC Name Graphical Symbol Truth Table S–R S Q R Q S R 0 0 0 1 1 Qn Qn!1 1 0 – 0 1 1 J–K J Q K Q J K 0 0 0 1 1 Qn Qn Qn!1 1 00 1 1 D D Q Q D 0 0 1 Qn!1 1 Ck Ck Ck Figure 11.27 Basic Flip-Flops causing the output to be 1; if only the K input is asserted, the result is a reset function, causing the output to be 0. When both J and K are 1, the function performed is referred to as the toggle function: the output is reversed. Thus, if Q is 1 and 1 is applied to J and K, then Q becomes 0. The reader should verify that the implementation of Figure 11.26 produces this characteristic function. J K Q Q Clock Figure 11.26 J–K Flip-Flop 2017 Kiến trúc máy tính 83 NKK-HUST S-R Latch và các Flip-Flop S-R Latch S-R Flip-Flop J-K Flip-FlopD Flip Flop 2017 Kiến trúc máy tính 84 11.4 / SEQUENTIAL CIRCUITS 389 First, let us show that the circuit is bistable. Assume that both S and R are 0 and that Q is 0. The inputs to the lower NOR gate are Q = 0 and S = 0. Thus, the output Q = 1 means that the inputs to the upper NOR gate are Q = 1 and R = 0, which has the output Q = 0. Thus, the state of the circuit is internally consistent and remains stable as long as S = R = 0. A similar line of reasoning shows that the state Q = 1, Q = 0 is also stable for R = S = 0. Thus, this circuit can function as a 1-bit memory. We can view the output Q as the “value” of the bit. The inputs S and R serve to write the values 1 and 0, respec- tively, into memory. To see this, consider the state Q = 0, Q = 1, S = 0, R = 0. Suppose that S changes to the value 1. Now the inputs to the lower NOR gate are S = 1, Q = 0. After some time delay ^t, the output of the lower NOR gate will be Q = 0 (see Figure 11.23). So, at this point in time, the inputs to the upper NOR gate become R = 0, Q = 0. After another gate delay of ^t the output Q becomes 1. This is again a stable state. The inputs to the lower gate are now S = 1, Q = 1, which maintain the output Q = 0. As long as S = 1 and R = 0, the outputs will remain Q = 1, Q = 0. Furthermore, if S returns to 0, the outputs will remain unchanged. The R output performs the opposite function. When R goes to 1, it forces Q = 0, Q = 1 regardless of the previous state of Q and Q. Again, a time delay of 2^t occurs before the final state is established (Figure 11.23). The S–R latch can be defined with a table similar to a truth table, called a characteristic table, which shows the next state or states of a sequential circuit as a function of current states and inputs. In the case of the S–R latch, the state can be defined by the value of Q. Table 11.10a shows the resulting characteristic table. Observe that the inputs S = 1, R = 1 are not allowed, because these would pro- duce an inconsistent output (both Q and Q equal 0). The table can be expressed more compactly, as in Table 11.10b. An illustration of the behavior of the S–R latch is shown in Table 11.10c. S Q Q R Figure 11.22 The S–R Latch Implemented with NOR Gates CLOCKED S–R FLIP-FLOP The output of the S–R latch changes, after a brief time delay, in response to a change in the input. This is referred to as asynchronous operation. More typically, events in the digital computer are synchronized to a clock pulse, so that changes occur only when a clock pulse occurs. Figure 11.24 shows this 11.4 / SEQUENTIAL CIRCUITS 391 arrangement. This device is referred to as a clocked S–R flip-flop. Note that the R and S inputs are passed to the NOR gates only during the clock pulse. D FLIP-FLOP One problem with S–R flip-flop is that the condition R = 1, S = 1 must be avoided. One way to do this is to allow just a single input. The D flip-flop accomplishes this. Figure 11.25 shows a gate implementation of the D flip-flop. By using an inverter, the nonclock inputs to the two AND gates are guaranteed to be the opposite of each other. The D flip-flop is sometimes referred to as the data flip-flop because it is, in effect, storage for one bit of data. The output of the D flip-flop is always equal to the most recent value applied to the input. Hence, it remembers and produces the last input. It is also referred to as the delay flip-flop, because it delays a 0 or 1 applied to its input for a single clock pulse. We can capture the logic of the D flip-flop in the following truth table: D Qn!1 0 0 1 1 J–K FLIP-FLOP Another useful flip-flop is the J–K flip-flop. Like the S–R flip-flop, it has two inputs. However, in this case all possible combinations of input values are valid. Figure 11.26 shows a gate implementation of the J–K flip-flop, and Figure 11.27 shows its characteristic table (along with those for the S–R and D flip-flops). Note that the first three combinations are the same as for the S–R flip-flop. With no input asserted, the output is stable. If only the J input is asserted, the result is a set function, S R Q Q Clock Figure 11.24 Clocked S–R Flip-Flop D Q Q Clock Figure 11.25 D Flip-Flop 11.4 / SEQUENTIAL CIRCUITS 391 arr ngement. This device is referred to as a clocked S–R flip-flop. Note th t the R and S inputs are passed to the NOR gates only during the clock p lse. D FLIP-FLOP One problem with S–R flip-flop is that the condition R = 1, S = 1 must be avoided. One way to do this is to allow just a single input. The D flip-flop accomplishes this. Figure 11.25 shows a gate implementation of the D flip-flop. By using an inverter, the nonclock inputs to the two AND gates are guaranteed to be the opposite of each other. The D flip-flop is sometimes referred to as the data flip-flop because it is, in effect, storage for one bit of data. The output of the D flip-flop is always equal to the most recent value applied to the input. Hence, it remembers and produces the last input. It is also referred to as the delay flip-flop, because it delays a 0 or 1 applied to its input for a single clock pulse. We can capture the logic of the D flip-flop in the following truth table: D Qn!1 0 0 1 1 J–K FLIP-FLOP Another useful flip-flop is the J–K flip-flop. Like the S–R flip-flop, it has two inputs. However, in this case all possible combinations of input values are valid. Figure 11.26 shows a gate implementation of the J–K flip-flop, and Figure 11.27 shows its characteristic table (along with those for the S–R and D flip-flops). Note that the first three combinations are the same as for the S–R flip-flop. With no input asserted, the output is stable. If only the J input is asserted, the result is a set function, S R Q Q Clock Figure 11.24 Clocked S–R Flip-Flop D Q Q Clock Figure 11.25 D Flip-Flop 392 CHAPTER 11 / DIGITAL LOGIC Name Graphical Symbol Truth Table S–R S Q R Q S R 0 0 0 1 1 Qn Qn!1 1 0 – 0 1 1 J–K J Q K Q J K 0 0 0 1 1 Qn Qn Qn!1 1 00 1 1 D D Q Q D 0 0 1 Qn!1 1 Ck Ck Ck Figure 11.27 Basic Flip-Flops causing the output to be 1; if only the K input is asserted, the result is a reset function, causing the output to be 0. When both J and K are 1, the function performed is referred to as the toggle function: the output is reversed. Thus, if Q is 1 and 1 is applied to J and K, then Q becomes 0. The reader should verify that the implementation of Figure 11.26 produces this characteristic function. J K Q Q Clock Figure 11.26 J–K Flip-Flop NKK-HUST Thanh ghi 8-bit song song 11.4 / SEQUENTIAL CIRCUITS 393 Registers As an example of the use of flip-flops, let us first examine one of the essential ele- ments of the CPU: the register. As we know, a register is a digital circuit used within the CPU to store one or more bits of data. Two basic types of registers are com- monly used: parallel registers and shift registers. PARALLEL EGISTERS A parallel register consists of a set of 1-bit memories that can be read or written simultaneously. It is used to store data. The registers that we have discussed throughout this book are parallel registers. The 8-bit register of Figure 11.28 illustrates the operation of a parallel register using D flip-flops. A control signal, labeled load, controls writing into the register from signal lines, D11 through D18. These lines might be the output of multiplexers, so that data from a variety of sources can be loaded into the register. SHIFT REGISTER A shift register accepts and/or transfers information serially. Consider, for example, Figure 11.29, which shows a 5-bit shift register constructed from clocked D flip-flops. Data are input only to the leftmost flip-flop. With each clock pulse, data are shifted to the right one position, and the rightmost bit is transferred out. Shift registers can be used to interface to serial I/O devices. In addition, they can be used within the ALU to perform logical shift and rotate functions. In this D D08 D18 Clk Q D Clk Q D Clk Q D Clk Q D Clk Q D Clk Q D Clk Q D Clk Q Clock Load D17 D16 D15 D14 D13 D12 D11 D07 D06 D05 Output lines Data lines D04 D03 D02 D01 Figure 11.28 8-Bit Parallel Register D Clk Q D Clk Q D Clk Q D Clk Q D Clk Q Clock Serial in Serial out Figure 11.29 5-Bit Shift Register 2017 Kiến trúc máy tính 85 NKK-HUST Thanh ghi dịch 5-bit 11.4 / SEQUENTIAL CIRCUITS 393 Registers As an example of the use of flip-flops, let us first examine one of the essential ele- ments of the CPU: the register. As we know, a register is a digital circuit used within the CPU to store one or more bits of data. Two basic types of registers are com- monly used: parallel registers and shift registers. PARALLEL REGISTERS A parallel register consists of a set of 1-bit memories that can be read or written simultaneously. It is used to store data. The registers that we have discussed throughout this book are parallel registers. The 8-bit register of Figure 11.28 illustrates the operation of a parallel register using D flip-flops. A control signal, labeled load, controls writing into the register from signal lines, D11 through D18. These lines might be the output of multiplexers, so that data from a variety of sources can be loaded into the register. SHIFT REGISTER A shift register accepts and/or transfers information serially. Consider, for example, Figure 11.29, which shows a 5-bit shift register constructed from clocked D flip-flops. Data are input only to the leftmost flip-flop. With each clock pulse, data are shifted to the right one position, and the rightmost bit is transferred out. Shift registers can be used to interface to serial I/O devices. In addition, they can be used within the ALU to perform logical shift and rotate functions. In this D D08 D18 Clk Q D Clk Q D Clk Q D Clk Q D Clk Q D Clk Q D Clk Q D Clk Q Clock Load D17 D16 D15 D14 D13 D12 D11 D07 D06 D05 Output lines Data lines D04 D03 D02 D01 Figure 11.28 8-Bit Parallel Register D Clk Q D Clk Q D Clk Q D Clk Q D Clk Q Clock Serial in Serial out Figure 11.29 5-Bit Shift Register 2017 Kiến trúc máy tính 86 NKK-HUST Bộ đếm 4-bit 394 CHAPTER 11 / DIGITAL LOGIC latter capacity, they need to be equipped with parallel read/write circuitry as well as serial. Counters Another useful category of sequential circuit is the counter. A counter is a register whose value is easily incremented by 1 modulo the capacity of the register; that is, after the maximum value is achieved the next increment sets the counter value to 0. Thus, a register made up of n flip-flops can count up to 2n - 1. An example of a counter in the CPU is the program counter. Counters can be designated as asynchronous or synchronous, depending on the way in which they operate. Asynchronous counters are relatively slow because the output of one flip-flop triggers a change in the status of the next flip-flop. In a synchronous counter, all of the flip-flops change state at the same time. Because the latter type is much faster, it is the kind used in CPUs. However, it is useful to begin the discussion with a description of an asynchronous counter. RIPPLE COUNTER An asynchronous counter is also referred to as a ripple counter, because the change that occurs to increment the counter starts at one end and “ripples” through to the other end. Figure 11.30 shows an implementation of a 4-bit counter using J–K flip-flops, together with a timing diagram that illustrates its behavior. The timing diagram is idealized in that it does not show the propagation delay that occurs as the signals move down the series of flip-flops. The output of the leftmost flip-flop (Q0) is the least significant bit. The design could clearly be extended to an arbitrary number of bits by cascading more flip-flops. J Q Q0 Q0 Q1 Q2 Q3 K Q Ck J Q Q1 K Q Ck J Q Q2 K Q Ck J Q Q3 K Q CkClock Clock High (a) Sequential circuit (b) Timing diagram Figure 11.30 Ripple Counter 2017 Kiến trúc máy tính 87 NKK-HUST Hết chương 2 2017 Kiến trúc máy tính 88
File đính kèm:
 bai_giang_kien_truc_may_tinh_chuong_2_co_ban_ve_logic_so_ngu.pdf
bai_giang_kien_truc_may_tinh_chuong_2_co_ban_ve_logic_so_ngu.pdf

