Bài giảng Kiến trúc máy tính - Chương 10: Số học máy tính - Nguyễn Hằng Phương
NỘI DUNG
10.1 Đơn vị Số học & Logic (ALU)
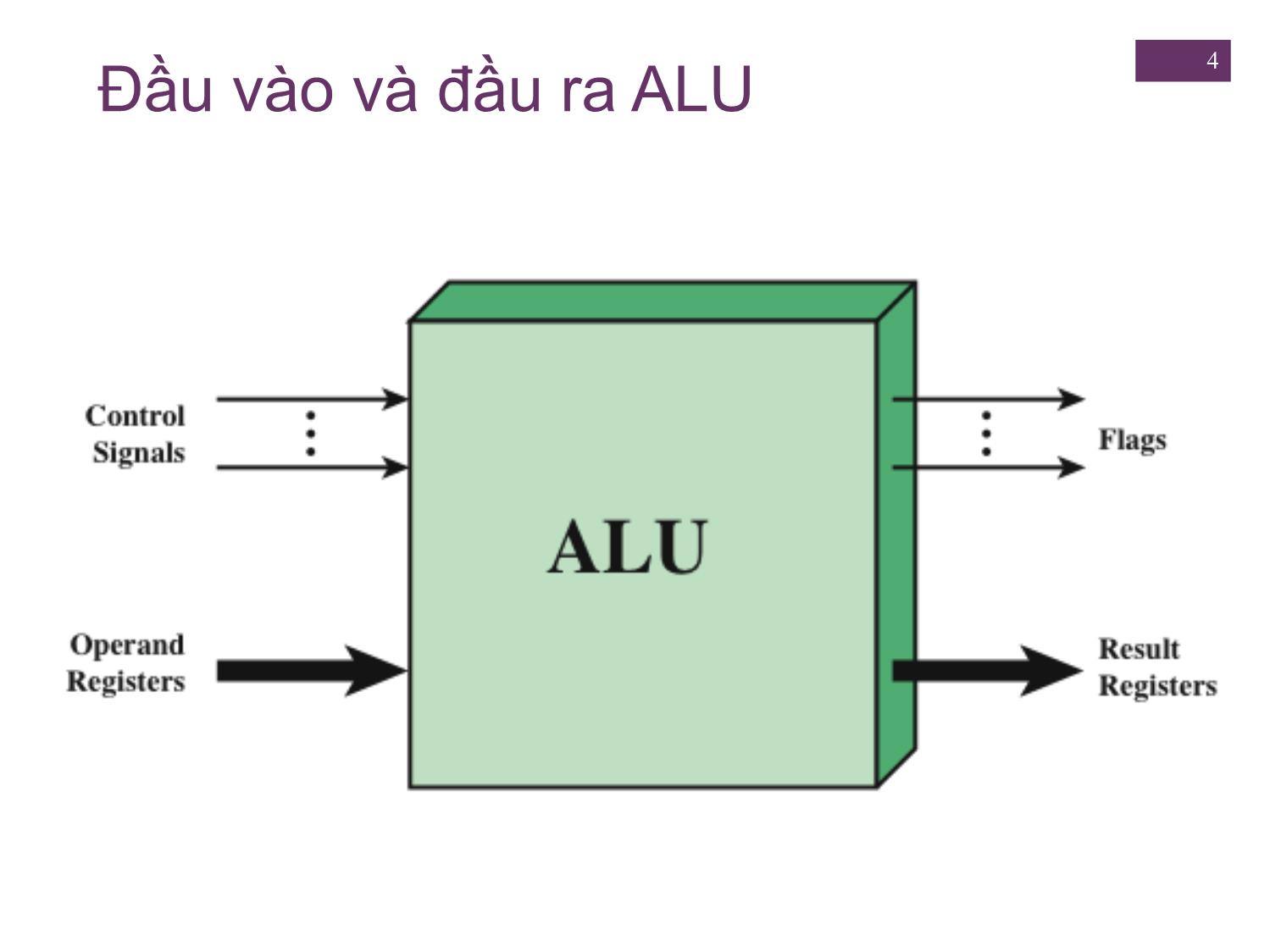
10.2 Biểu diễn số nguyên
Biểu diễn Dấu-độ lớn
Biểu diễn bù 2
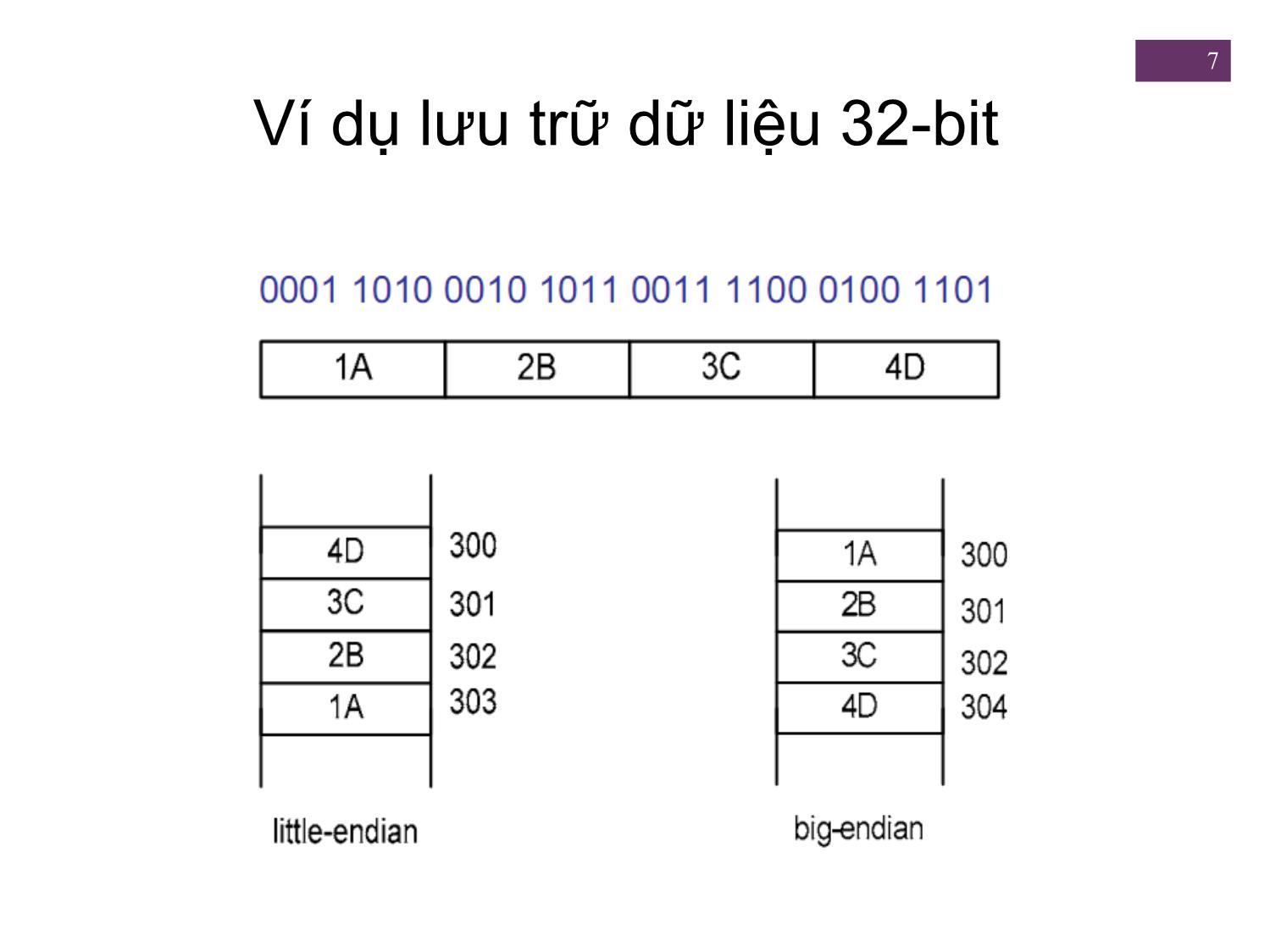
Mở rộng phạm vi
Biểu diễn dấu chấm tĩnh
10.3 Số học số nguyên
phép đảo/ Cộng và trừ / Phép nhân / Phép chia
10.4 Biểu diễn dấu chấm động
10.5 Số học dấu chấm động

Trang 1

Trang 2

Trang 3
Trang 4
Trang 5

Trang 6
Trang 7

Trang 8

Trang 9

Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Kiến trúc máy tính - Chương 10: Số học máy tính - Nguyễn Hằng Phương", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Kiến trúc máy tính - Chương 10: Số học máy tính - Nguyễn Hằng Phương

1 + Chương 10 Số học máy tính + 2 NỘI DUNG 10.1 Đơn vị Số học & Logic (ALU) 10.2 Biểu diễn số nguyên Biểu diễn Dấu-độ lớn Biểu diễn bù 2 Mở rộng phạm vi Biểu diễn dấu chấm tĩnh 10.3 Số học số nguyên phép đảo/ Cộng và trừ / Phép nhân / Phép chia 10.4 Biểu diễn dấu chấm động 10.5 Số học dấu chấm động + 3 1. Đơn vị logic & số học (ALU) Phần của máy tính thực hiện phép toán số học và lôgíc trên dữ liệu Tất cả các bộ phận khác trong hệ thống máy tính đưa dữ liệu tới ALU để ALU xử lý rồi sau đó nhận lại kết quả Sử dụng các linh kiện logic số đơn giản để lưu trữ các chữ số nhị phân và thực hiện các phép toán logic Boolean đơn giản Đầu vào và đầu ra ALU 4 5 Mã hóa dữ liệu trong máy tính . Mọi dữ liệu đưa vào máy tính đều phải được mã hóa thành số nhị phân . Mã hóa theo các chuẩn qui ước . Dữ liệu số: . „Số nguyên: mã hóa theo một số chuẩn . Số thực: mã hóa bằng số dấu chấm động . Dữ liệu ký tự: mã hóa theo bộ mã ký tự 6 Thứ tự lưu trữ byte trong bộ nhớ chính . Bộ nhớ chính thường tổ chức theo byte . Hai cách lưu trữ dữ liệu nhiều byte: . Little-endian: . Byte có ý nghĩa thấp được lưu trữ ở ngăn nhớ có địa chỉ nhỏ, byte có ý nghĩa cao được lưu trữ ở ngăn nhớ có địa chỉ lớn. . Nền tảng sử dụng: Intel . Big-endian: . Byte có ý nghĩa cao được lưu trữ ở ngăn nhớ có địa chỉ nhỏ, byte có ý nghĩa thấp được lưu trữ ở ngăn nhớ có địa chỉ lớn. . Nền tảng sử dụng: IBM zSeries, Motorola 680x0 7 Ví dụ lưu trữ dữ liệu 32-bit + 8 2. Biểu diễn số nguyên Số nguyên không dấu (Unsigned Integer) Số nguyên có dấu (Signed Integer) Trong hệ nhị phân, có thể biểu diễn các số bất kì bằng: Các chữ số 0 và 1 Dấu âm (với số âm) dấu chấm (với số có phần phân số) Đối với mục đích lưu trữ và xử lý, sẽ không có lợi khi dùng các ký hiệu đặc biệt cho dấu trừ và dấu chấm Chỉ sử dụng các chữ số nhị phân (0,1) để biểu diễn số? 9 a. Biểu diễn số nguyên không dấu Nguyên tắc tổng quát: Dùng n bit biểu diễn số nguyên không dấu A: Dải biểu diễn của A: từ 0 đến 2n –1 Với n = 8 bit: Biểu diễn được các giá trị từ 0 đến 255 0000 0000 = 0 0000 0001 = 1 0000 0010 = 2 ... 1111 1111 = 255 b. Biểu diễn dấu-độ lớn 10 . Quy ước về biểu diễn số nguyên âm và dương: dùng bit quan trọng nhất (MSB) trong từ làm bit dấu • bit dấu là 0 số dương • bit dấu là 1 số âm . Ví dụ: + 18 = 00010010 - 18 = 10010010 . Biểu diễn dấu-độ lớn: cách sử dụng bit dấu đơn giản nhất . Nhược điểm: • Để thực hiện phép cộng và phép trừ, đòi hỏi phải xem xét cả dấu và độ lớn của các số • Có hai biểu diễn của số 0 (+0 và -0) . Biểu diễn dấu-độ lớn hiếm khi được sử dụng trong việc xử lý phần số nguyên của ALU 11 c. Biểu diễn bù 2 Nguyên tắc tổng quát: Dùng n bit biểu diễn số nguyên có dấu A: Với A là số dương: bit an-1 = 0, các bit còn lại biểu diễn độ lớn như số không dấu Với A là số âm: được biểu diễn bằng số bù hai của số dương tương ứng, bit an-1 = 1 Quy tắc tìm số bù hai Số bù một của A = đảo giá trị các bit của A (Số bù hai của A) = (Số bù một của A) + 1 Ví dụ: +3 = 0000 0011 -3 = 1111 1101 12 + c. Biểu diễn bù 2 Sử dụng bit quan trọng nhất làm bit dấu Có 1 biểu diễn cho số 0 Phạm vi biểu diễn: (– 2n-1) (2n-1 -1) Dải biểu diễn cho số dương: 0 đến 2n-1 -1 Dải biểu diễn cho số âm: -1 đến - 2n-1 Thực hiện phép toán số học dễ dàng Để tính A – B, lấy bù 2 của B rồi cộng với A Khi cộng 2 số cùng dấu, nếu kết quả có dấu ngược lại sẽ gây tràn (overflow) được sử dụng trong việc xử lý phần số nguyên của ALU 13 Biểu diễn số nguyên 4-Bit + 14 d. Mở rộng phạm vi Mở rộng phạm vi biểu diễn số nguyên bằng cách tăng độ dài chuỗi bit Mở rộng phạm vi trong biểu diễn dấu-độ lớn: di chuyển bit dấu tới vị trí mới ngoài cùng bên trái và điền thêm các bit 0 Mở rộng phạm vi trong biểu diễn số âm bù 2: di chuyển bit dấu tới vị trí ngoài cùng bên trái và điền vào các bit giống bit dấu Đối với số dương thì điền 0, và số âm thì điền số 1 Đây được gọi là phần mở rộng dấu 15 + Phạm vi biểu diễn số co dấu bù 2: (– 2n-1) (2n-1 -1) Bù 2 8 bit +127 = 01111111 = 27 -1 -128 = 10000000 = -27 Bù 2 16 bit +32767 = 011111111 11111111 = 215 - 1 -32768 = 100000000 00000000 = -215 Ví dụ Mở rộng phạm vi Số dương được điền các bit 0 +18 = 00010010 +18 = 00000000 00010010 Số âm được điền các bit 1 -18 = 10010010 -18 = 11111111 10010010 + 3. Số học số nguyên 16 17 + a. Phép đảo dấu Phép đảo dấu = lấy bù 2: Đảo các bit của số nguyên (cả bit dấu) Kết quả coi như số nguyên nhị phân không dấu, cộng thêm 1 +18 = 00010010 (bù 2) đảo bit = 11101101 + 1 11101110 = -18 Đảo của đảo của một số là chính nó: -18 = 11101110 (bù 2) đảo bit = 00010001 + 1 00010010 = +18 + 18 Phép đảo - Trường hợp đặc biệt . 0 = 0000 0000 (bù 2) Đảo bit 1111 1111 Cộng 1 +1 Kết quả 1 0000 0000 Bỏ qua bit tràn: - 0 = 0 . -128 = 10000000 (bù 2) Đảo bit 01111111 Cộng 1 +1 Kết quả 10000000 Vậy: -(-128) = -128 X 19 b. Phép cộng Cộng như số nguyên không dấu 20 Nguyên tắc NGUYÊN TẮC TRÀN: Nếu hai số cộng với nhau, mà cả hai đều dương hoặc đều Tràn âm, thì sẽ xảy ra tràn nếu kết quả có dấu ngược lại. + 21 b. Phép trừ 22 Nguyên tắc NGUYÊN TẮC TRỪ: Để trừ một số (số bị trừ) từ một số khác (số trừ), lấy bù 2 Trừ (đảo) của số trừ và cộng nó với số bị trừ. + VD: a - b = a + (-b) 23 Mô tả hình học của số nguyên bù 2 endpoints are joined Phần cứng thực hiện cộng và trừ 24 25 d. Phép nhân . Phức tạp . Tính tích cho từng chữ số - tích riêng phần . Quan tâm đến vị trí giá trị (dóng cột) . Cộng tổng các tích tích toàn phần . Ví dụ nhân số nguyên không dấu: ! Kết quả dài gấp đôi 26 Sơ đồ luồng của phép nhân nhị phân không dấu + Phần cứng thực hiện nhân nhị phân không dấu + 28 Phép nhân bù 2 (nhân có dấu) Nhân hai số nguyên 4 bit không dấu thu được kết quả 8 bit Nhân 1 số nhị phân với 2n được thực hiện bằng cách dịch số đó sang trái n bit + 29 So sánh So sánh phép nhân số nguyên không dấu và số bù 2 30 Thuật toán Booth M Q 31 Ví dụ thuật toán Booth 32 Ví dụ thuật toán Booth 33 e. Phép chia . Phức tạp hơn phép nhân . Ví dụ: phép chia 2 số nguyên nhị phân không dấu Thuật toán chia restoring bù 2 Input: M – số chia dương Q – số bị chia dương Output: Q – thương A – dư Begin A 0 Lặp n lần Dịch trái A, Q A A – M Bit dấu của A= 1 Q0 0 và A A + M Else Q0 1 End + 35 Ví dụ chia Restoring bù 2 (7/3) + 36 4. Dấu chấm động Biểu diễn dấu chấm tĩnh có thể biểu diễn một dải số nguyên dương và nguyên âm xung quanh gốc 0 Biểu diễn số thực dùng dấu chấm tĩnh: 1001.1010 = 23 + 20 +2-1 + 2-3 = 9.625 Hạn chế: Không thể biểu diễn số rất lớn hoặc phân số rất nhỏ Phần phân số trong thương của một phép chia hai số lớn có thể bị mất 37 Biểu diễn dấu chấm động Một số thực bất kỳ được biểu diễn kiểu dấu chấm động như sau: Trong đó: S : phần định trị B: cơ số E : số mũ – Số mũ tương ứng với vị trí dấu chấm 38 Chuẩn IEEE 754 . Các quy ước quan trọng nhất về biểu diễn dấu chấm động . Hỗ trợ khả năng di động chương trình từ bộ xử lý này sang bộ xử lý khác và khuyến khích sự phát triển các chương trình số học tinh vi hơn . Chuẩn được công nhận rộng rãi và được sử dụng trên hầu hết các bộ xử lý hiện đại và bộ xử lý số học . IEEE 754-2008 bao trùm cả biểu diễn dấu chấm động nhị phân và thập phân 39 Định dạng IEEE 754 40 Biểu diễn bias bias = (2n-1 - 1), với n là số bit biểu diễn Dải biểu diễn: (0 – bias) (2n – 1 – bias) Số A = Biểu diễn bias của A – bias Ví dụ: 41 Định dạng dấu chấm động 32-bit d e m • Bit dấu d = 0 dương; d = 1 âm • Cơ số B = 2 • Bias = 127 cho trường mũ 8 bit • Số mũ E = e – 127 • 23 bit định trị m chứa phần lẻ của S (S = 1.m) • Công thức xác định giá trị của số: X = (-1)d * 1.m * 2e-127 + Phần định trị 42 Phần phía sau của một từ Một số dấu chấm động có thể biểu diễn dưới nhiều dạng Các cách viết sau đây là tương đương, trong đó phần định trị được biểu diễn dưới dạng nhị phân: 0.110 * 25 110 * 22 0.0110 * 26 Số nhị phân chuẩn hoá Bit có trọng số lớn nhất của phần định trị khác 0 Biểu diễn nhị phân chuẩn hoá: Ví dụ 1 43 Xác định giá trị của số thực được biểu diễn bằng 32-bit sau: 1100 0001 0101 0110 0000 0000 0000 0000 „ d = 1 số âm „ e = 1000 00102 = 13010 E = 130 -127 = 3 m = 101 0110 0000 0000 0000 0000 Vậy X = -1.101011 * 23 = -1101.011 = -13.375 Ví dụ 2 44 Biểu diễn số X= 83.75 về dạng số dấu phẩy động 32-bit Giải: 6 „ X = 83.75(10) = 1010011.11(2) = 1.01001111 x 2 „ Ta có: d = 0 vì đây là số dương E = e – 127 = 6 e= 127 + 6 = 133(10) = 1000 0101(2) Vậy: X = 0100 0010 1010 0111 1000 0000 0000 0000 + 45 Dải số biểu diễn được + 47 Mật độ số dấu chấm động Các số được biểu diễn trong dấu chấm động không cách đều trên trục số. Nhược điểm của dấu chấm động: biểu diễn nhiều số không chính xác và phải làm tròn thành giá trị gần nhất có thể biểu diễn được. + 48 5. Số học dấu chấm động Các trường hợp tràn: Overflow mũ: số mũ dương vượt quá giá trị mũ lớn nhất có thể biểu diễn. Coi là +∞ hoặc - ∞ Underflow mũ: số mũ âm nhỏ hơn giá trị mũ nhỏ nhất có thể biểu diễn. Coi là 0 Underflow định trị: khi dóng phần định trị, các chữ số có thể bị vượt ra phía bên phải phần định trị Overflow định trị: cộng 2 phần định trị cùng dấu có thể ảnh hưởng bit quan trọng nhất 49 Số và Phép tính dấu chấm động 50 Cộng và trừ dấu chấm động Bốn giai đoạn cơ bản của thuật toán cộng và trừ: 1. Kiểm tra các số hạng có bằng 0 hay không 2. Căn chỉnh phần định trị (thay đổi số mũ). 3. Cộng hoặc trừ các định trị. 4. Chuẩn hóa kết quả. Cộng và trừ dấu chấm động 51 52 Nhân và chia dấu chấm động 1. Kiểm tra 0 2. Cộng/trừ số mũ 3. Nhân/chia các định trị (xem dấu) 4. Chuẩn hóa 5. Làm tròn 6. Tất cả các kết quả được lưu trữ với độ dài gấp đôi + Phép nhân dấu chấm động + Phép chia dấu chấm động + 55 Độ chính xác Guard Bits + 56 Độ chính xác Làm tròn 4 phương pháp theo chuẩn IEEE: Làm tròn gần nhất Làm tròn về phía +∞ Làm tròn về phía -∞ Làm tròn về phía 0 + 57 Số học khoảng phương pháp hiệu quả để kiểm soát lỗi trong tính toán dấu chấm động bằng cách tạo ra hai giá trị cho mỗi kết quả Rút gọn Hai giá trị đó tương ứng với điểm cuối biên dưới và điểm cuối biên trên của Làm tròn về phía 0 khoảng có chứa kết quả đúng Bỏ qua extra bit Độ rộng của khoảng cho biết độ chính Kỹ thuật đơn giản nhất xác của kết quả a consistent bias toward zero Nếu các điểm cuối không biểu diễn in the operation được thì điểm cuối của khoảng sẽ được làm tròn xuống và lên tương ứng serious bias because it affects Nếu khoảng giữa giới hạn trên và dưới every operation for which there đủ hẹp thì sẽ thu được một kết quả đủ are nonzero extra bits chính xác Làm tròn về phía dương vô cùng và âm vô cùng + 58 Chuẩn IEEE cho số học dấu chấm động nhị phân Vô cùng Được coi là trường hợp đặc biệt của số học thực, với các giá trị vô cùng được đưa ra như sau: - ∞ < (mọi số hữu hạn) < + ∞ Ví dụ: 5 + (+ ∞ ) = + ∞ 5÷ (+ ∞ ) = +0 5 - (+ ∞ ) = - ∞ (+ ∞ ) + (+ ∞ ) = + ∞ 5 + (- ∞ ) = - ∞ (- ∞ ) + (- ∞) = - ∞ 5 - (- ∞ ) = + ∞ (- ∞ ) - (+ ∞ ) = - ∞ 5 * (+ ∞ ) = + ∞ (+ ∞ ) - (- ∞ ) = + ∞ + Tổng kết 59 Số học máy tính Chương 10 Số học máy tính ALU phép đảo Biểu diễn số nguyên Cộng và trừ Biểu diễn dấu-độ lớn Nhân Biểu diễn bù 2 Chia Mở rộng phạm vi Số học dấu chấm động Biểu diễn dấu chấm tĩnh Cộng và trừ Biểu diễn dấu chấm động Nhân và chia Nguyên tắc Độ chính xác Chuẩn IEEE cho Biểu diễn Chuẩn IEEE cho số học dấu dấu chấm động nhị phân chấm động nhị phân + 60 Câu hỏi chương 10 1. Giải thích ngắn gọn về các biểu diễn: dấu-độ lớn, bù 2, biased. 2. Cách xác định một số là âm hay dương trong các biểu diễn: dấu-độ lớn, bù 2, biased. 3. Nguyên tắc mở rộng phạm vi biểu diễn số cho biểu diễn bù 2 là gì? 4. Cách đảo một số nguyên trong biểu diễn bù 2? 5. Phân biệt biểu diễn bù 2 của một số và bù 2 của một số? 6. Nếu coi 2 số bù 2 như là số nguyên không dấu khi thực hiện cộng, kết quả hiểu theo số bù 2 là chính xác. Điều này không đúng với phép nhân. Tại sao? 7. Bốn thành phần của một số trong biểu diễn dấu chấm động là gì? 8. Vì sao sử dụng biểu diễn bias cho số mũ của một số dấu chấm động? 9. Phân biệt tràn dương, tràn số mũ, và tràn định trị? 10. Các yếu tố cơ bản của phép cộng và trừ dấu chấm động là gì? 11. Lý do sử dụng guard bit? 12. Liệt kê bốn phương pháp làm tròn kết quả của phép toán dấu chấm động. + 61 Bài tập (1) 1. Biểu diễn số thập phân sau sang biểu diễn dấu-độ lớn và bù 2 nhị phân sử dụng 16 bit: a) +512 b) -29 c) -91 2. Biểu diễn các giá trị bù 2 sau ra dạng thập phân: a) 1101011 b) 0101101 3. Giả sử dùng biểu diễn bù 2 8 bit. Thực hiện phép tính: a) 6+13 b) -6+13 c) 6 – 13 d) -6 – 13 4. Thực hiện phép tính số học bù 2: + 62 Bài tập (2) 5/ x = 0101 và y = 1010 theo biểu diễn bù 2. Hãy tính tích p = x * y bằng thuật toán Booth. 6/ Tính 29*23 bằng thuật toán Booth, trong đó mỗi số biểu diễn bằng 6 bit. 7/ Biểu diễn các số sau theo định dạng IEEE 32-bit dấu chấm động: a) -5 b) -6 c) -1.5 d) 384 e) 1/16 f) -1/32 8/ Các số sau biểu diễn theo định dạng IEEE 32-bit dấu chấm động. Xác định giá trị hệ thập phân tương ứng? a. 1 10000011 11000000000000000000000 b. 0 01111110 10100000000000000000000 c. 0 10000000 00000000000000000000000
File đính kèm:
 bai_giang_kien_truc_may_tinh_chuong_10_so_hoc_may_tinh_nguye.pdf
bai_giang_kien_truc_may_tinh_chuong_10_so_hoc_may_tinh_nguye.pdf

