Bài giảng Kiến trúc máy tính 1 - Chương 4: Mạch logic số - Vũ Đức Lung
4.1. Cổng và đại số Boolean
4.1.1. Cổng (Gate)
4.1.2. Đại số Boolean
4.2. Bản đồ Karnaugh
4.3. Những mạch Logic số cơ bản
4.3.1. Mạch tích hợp (IC-Intergrate Circuit)
4.3.2. Mạch kết hợp (Combinational Circuit)
4.3.3. Bộ dồn kênh-bộ phân kênh
4.3.4. Mạch cộng (Adder)
4.3.5. Mạch giải mã và mã hóa

Trang 1

Trang 2
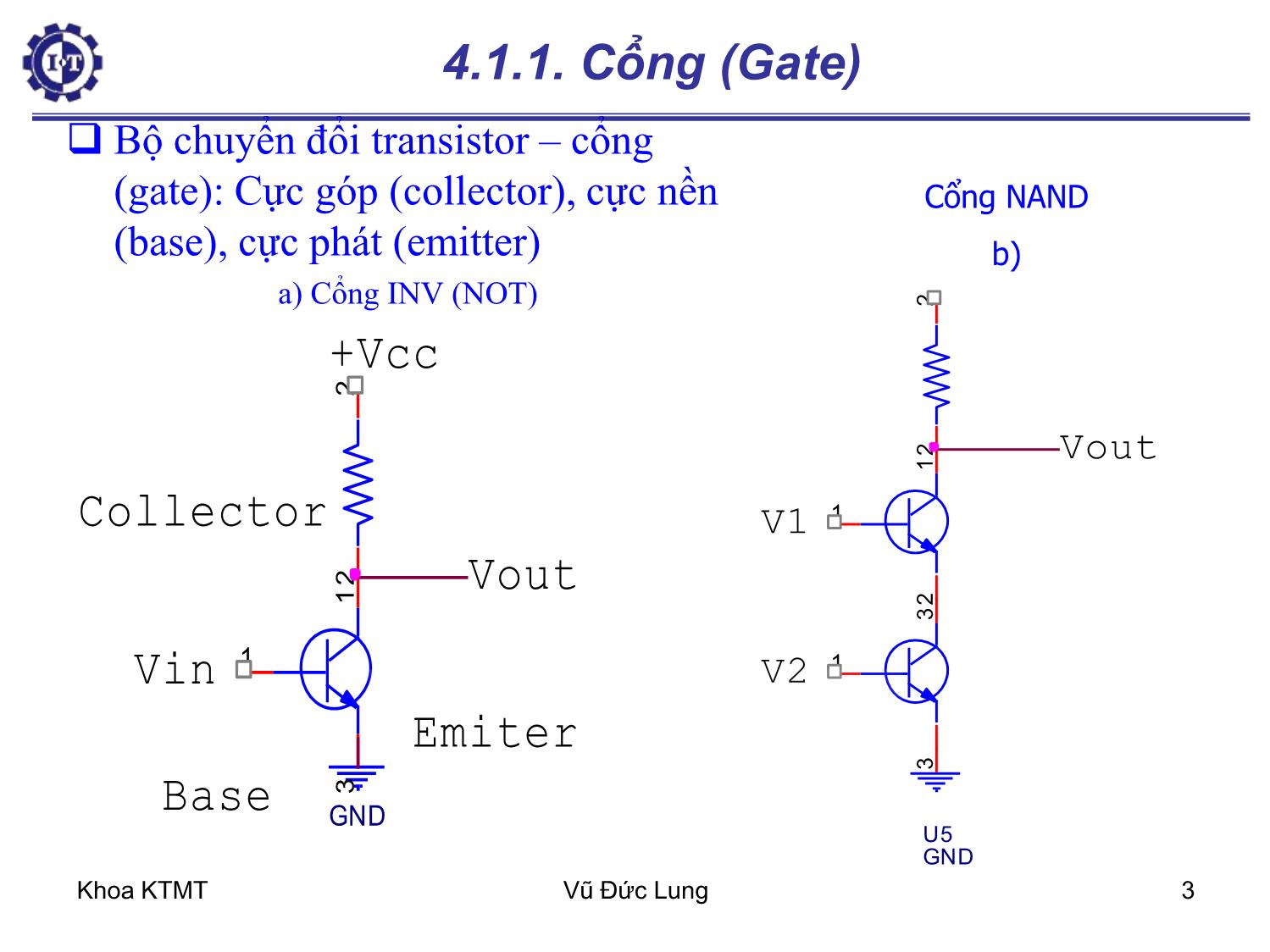
Trang 3
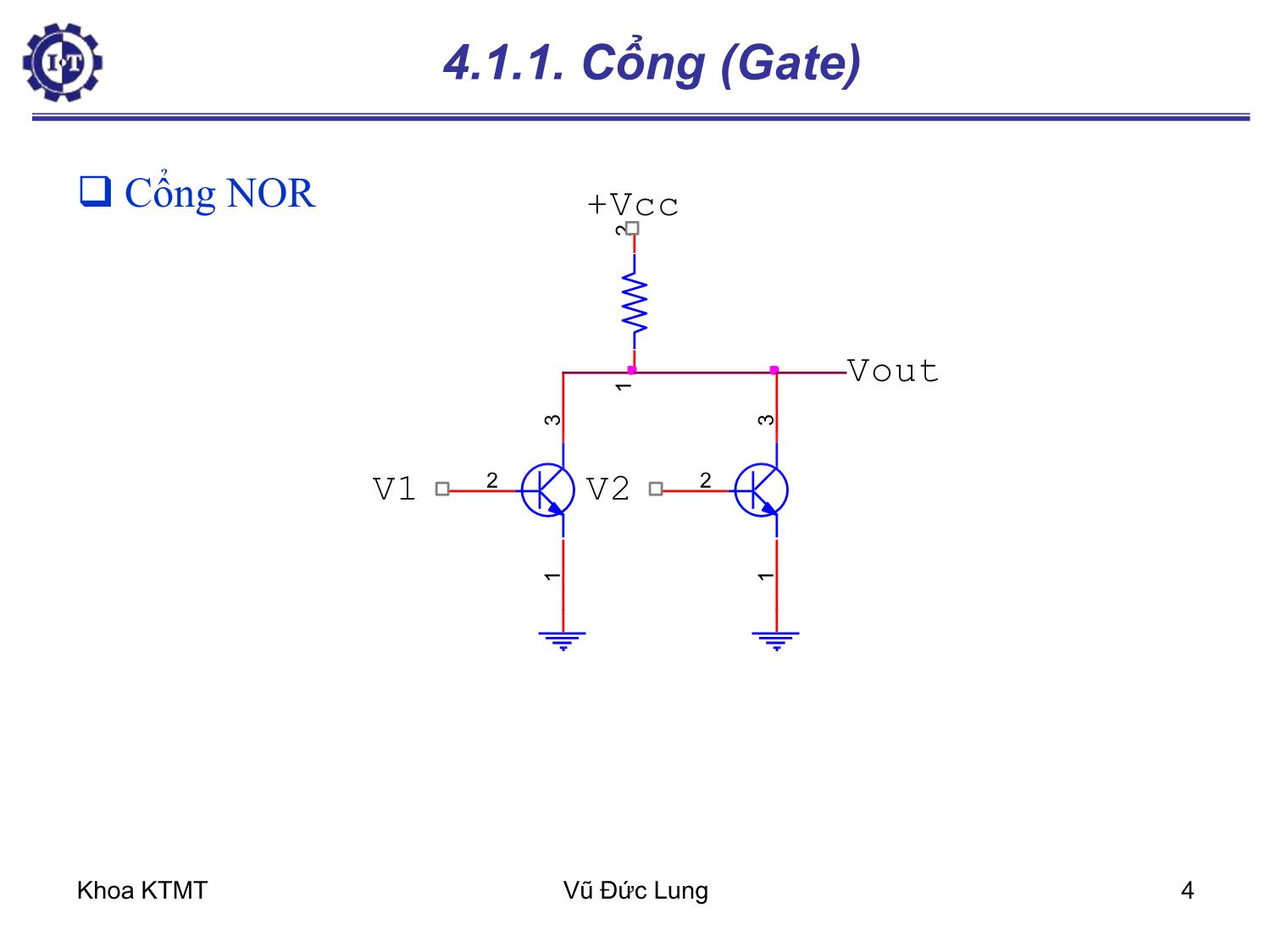
Trang 4
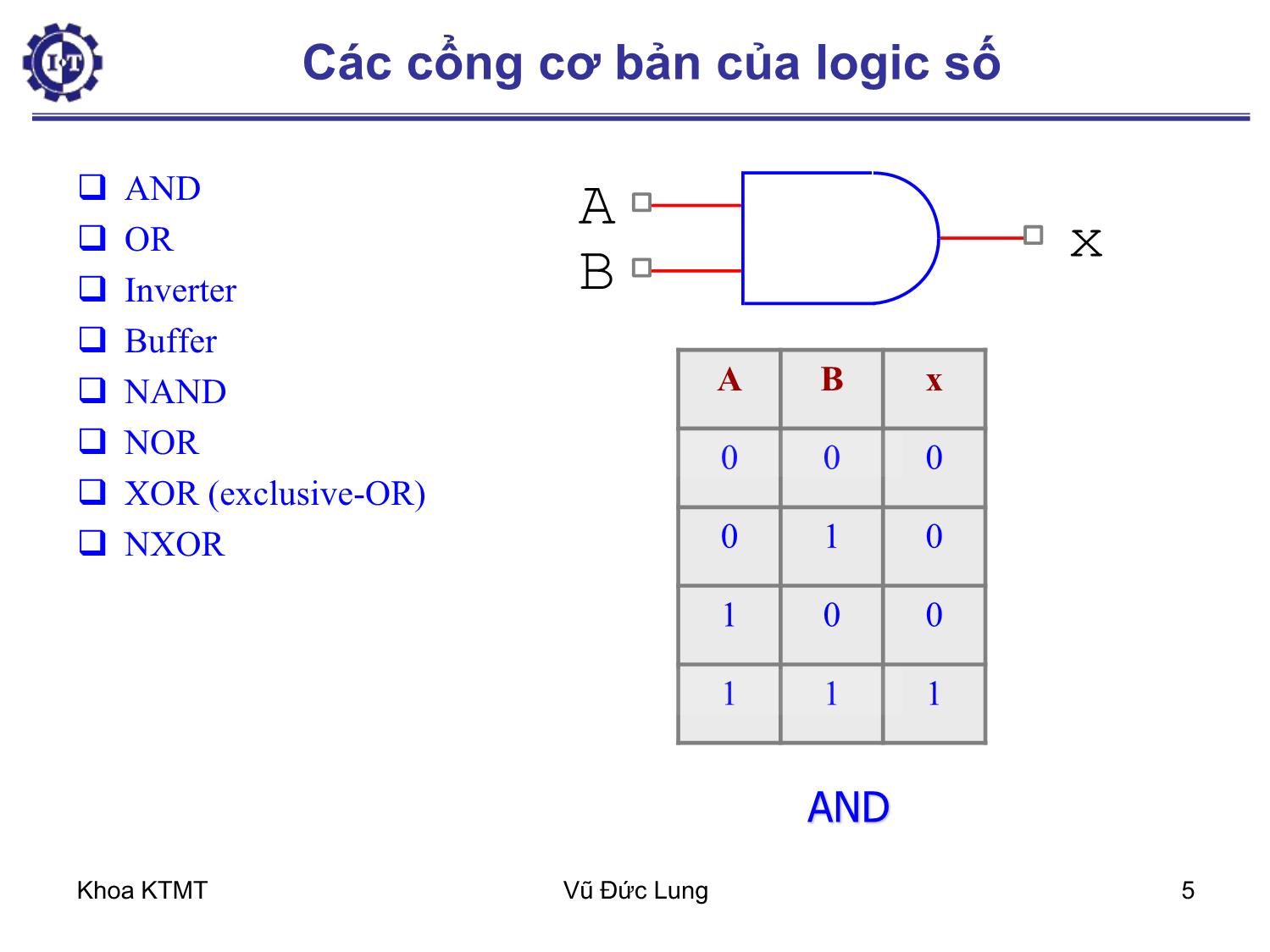
Trang 5
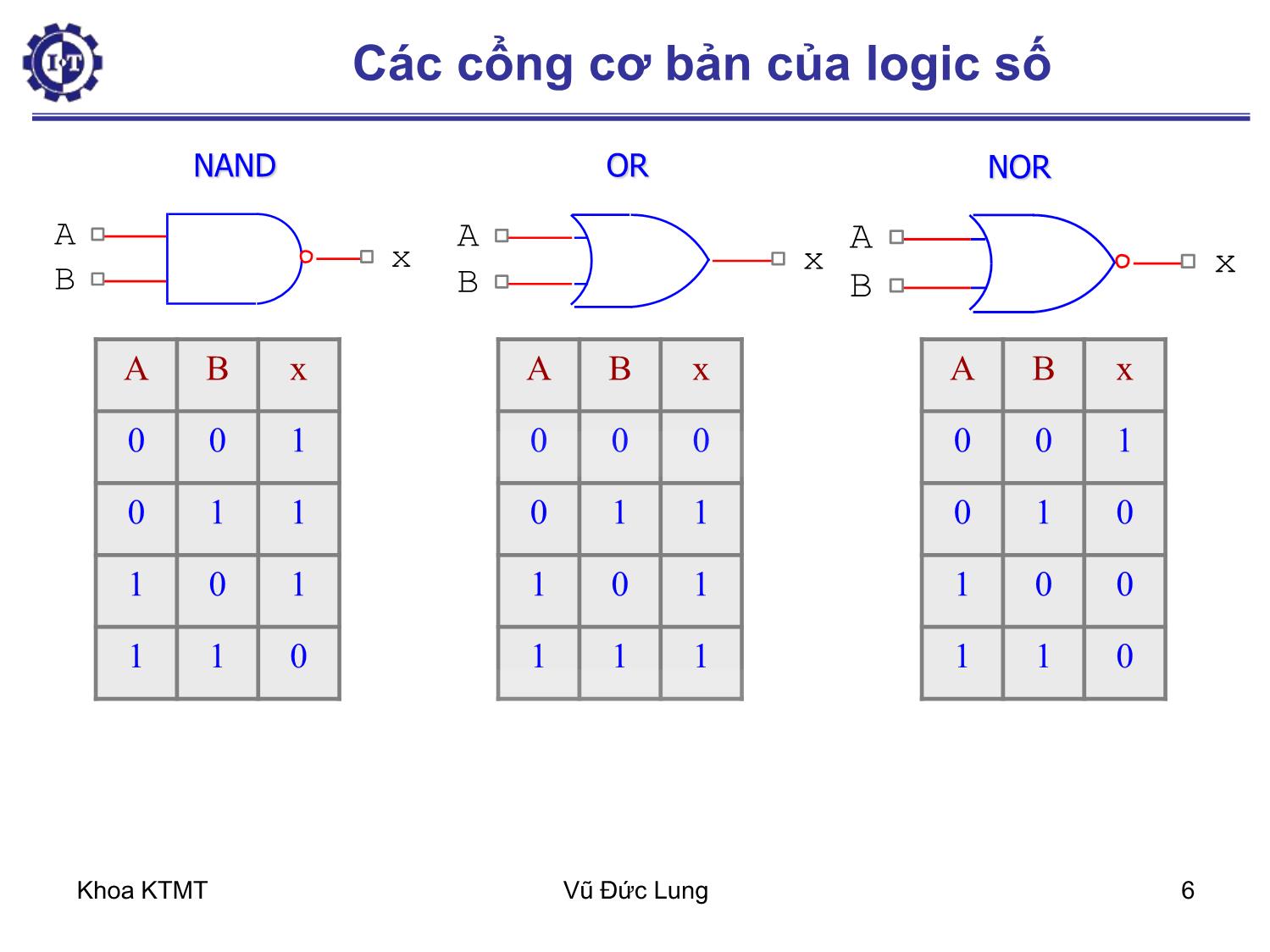
Trang 6
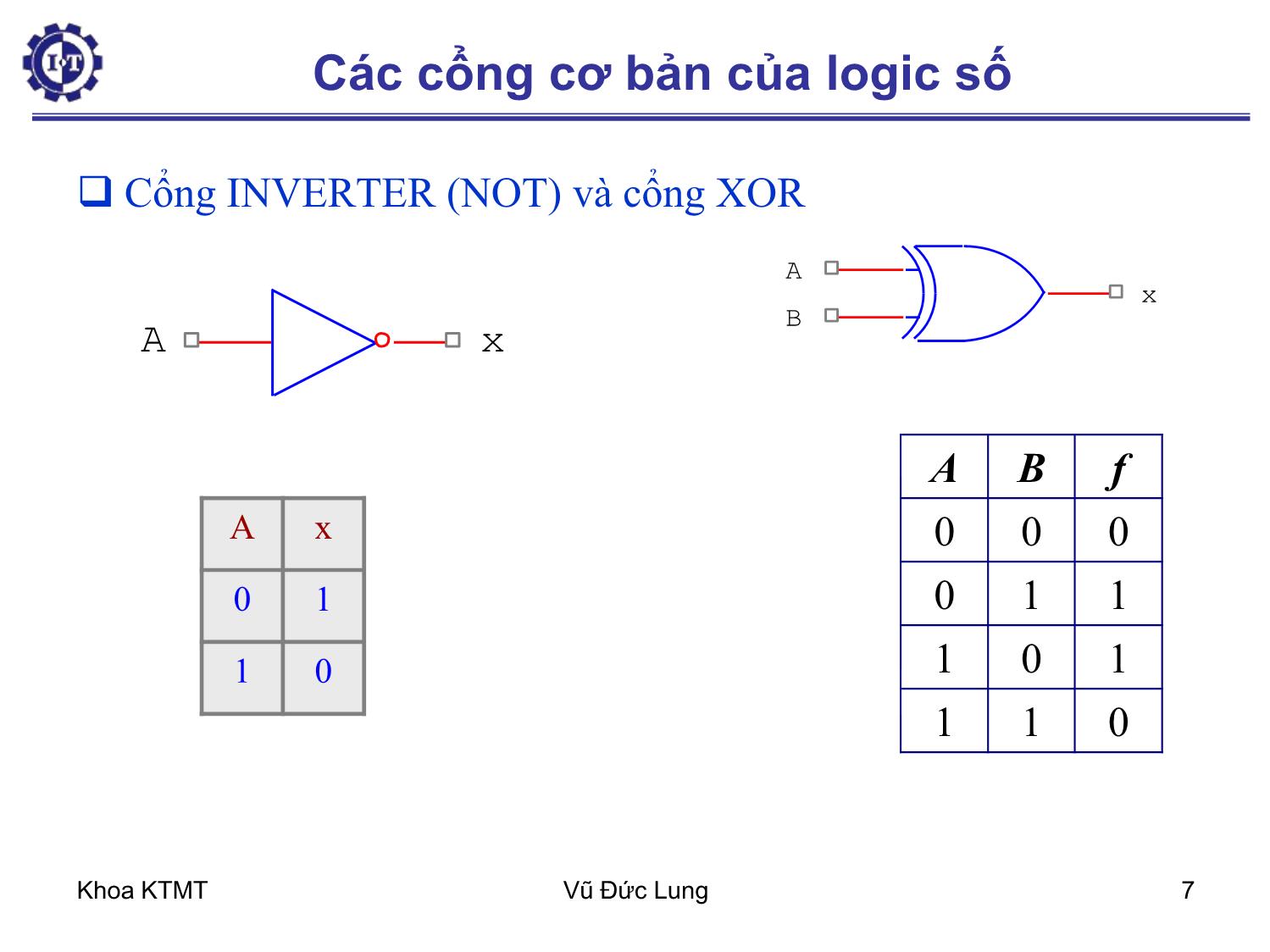
Trang 7

Trang 8
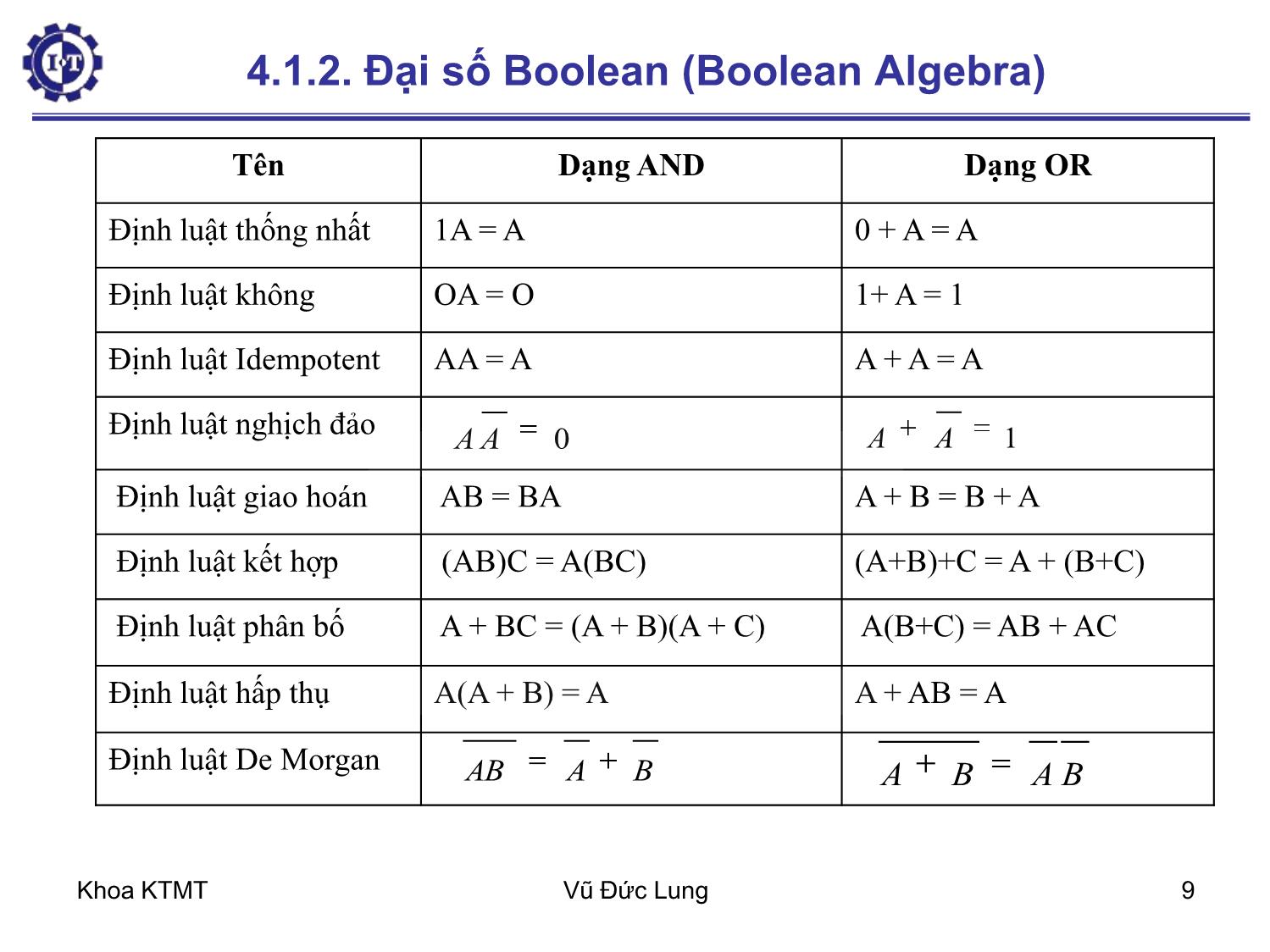
Trang 9
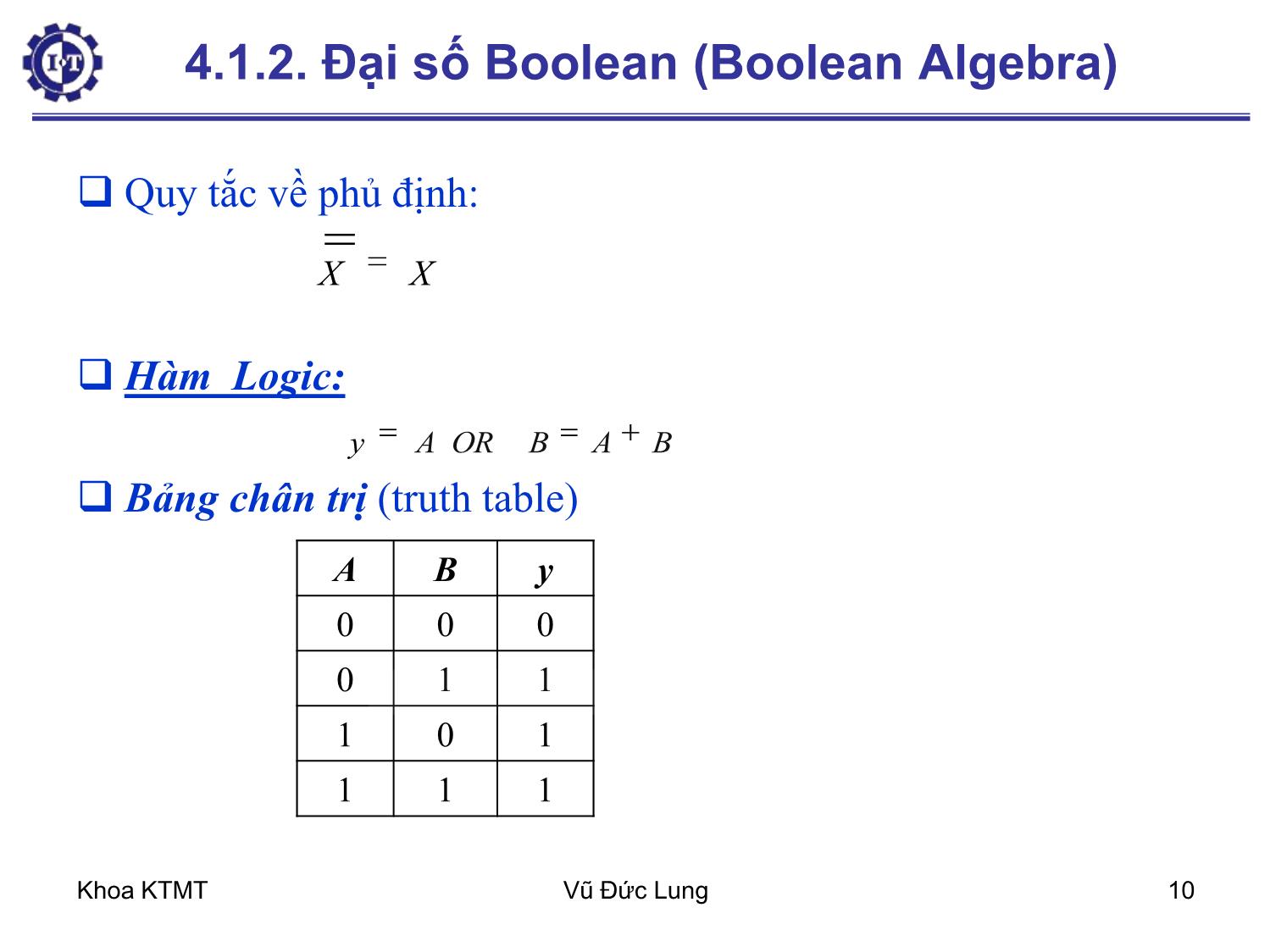
Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Kiến trúc máy tính 1 - Chương 4: Mạch logic số - Vũ Đức Lung", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Kiến trúc máy tính 1 - Chương 4: Mạch logic số - Vũ Đức Lung

Khoa KTMT Vũ Đức Lung 1 Chương 4 – Mạch Logic số 4.1. Cổng và đại số Boolean 4.1.1. Cổng (Gate) 4.1.2. Đại số Boolean 4.2. Bản đồ Karnaugh 4.3. Những mạch Logic số cơ bản 4.3.1. Mạch tích hợp (IC-Intergrate Circuit) 4.3.2. Mạch kết hợp (Combinational Circuit) 4.3.3. Bộ dồn kênh-bộ phân kênh 4.3.4. Mạch cộng (Adder) 4.3.5. Mạch giải mã và mã hóa Khoa KTMT Vũ Đức Lung 2 4.1. Cổng và đại số Boolean Mạch số là mạch trong đó chỉ hiện diện hai giá trị logic. Thường tín hiệu giữa 0 và 1 volt đại diện cho số nhị phân 0 và tín hiệu giữa 2 và 5 volt – nhị phân 1. Cổng – cơ sở phần cứng, từ đó chế tạo ra mọi máy tính số Gọi là cổng luận lý vì nó cho kết quả lý luận của đại số logic như nếu A đúng và B đúng thì C đúng (cổng A AND B = C) Khoa KTMT Vũ Đức Lung 3 Bộ chuyển đổi transistor – cổng (gate): Cực góp (collector), cực nền (base), cực phát (emitter) a) Cổng INV (NOT) Cổng NAND b) 1 2 GND 1 2 3 Vin Vout +Vcc Base Collector Emiter 1 2 1 2 3 1 2 3 U5 GND V1 V2 Vout 4.1.1. Cổng (Gate) Khoa KTMT Vũ Đức Lung 4 4.1.1. Cổng (Gate) Cổng NOR 1 2 3 1 3 2 1 3 2 Vout +Vcc V1 V2 Khoa KTMT Vũ Đức Lung 5 Các cổng cơ bản của logic số AND OR Inverter Buffer NAND NOR XOR (exclusive-OR) NXOR A B x A B x 0 0 0 0 1 0 1 0 0 1 1 1 AND Khoa KTMT Vũ Đức Lung 6 OR A B x A B x 0 0 0 0 1 1 1 0 1 1 1 1 A x B NAND A B x 0 0 1 0 1 1 1 0 1 1 1 0 A x B NOR A B x 0 0 1 0 1 0 1 0 0 1 1 0 Các cổng cơ bản của logic số Khoa KTMT Vũ Đức Lung 7 Cổng INVERTER (NOT) và cổng XOR A B f 0 0 0 0 1 1 1 0 1 1 1 0 A B x A x 0 1 1 0 A x Các cổng cơ bản của logic số Khoa KTMT Vũ Đức Lung 8 4.1.2. Đại số Boolean (Boolean Algebra) - Đại số Boolean được lấy theo tên người khám phá ra nó, nhà toán học người Anh George Boole. - Đại số Boolean là môn đại số trong đó biến và hàm chỉ có thể lấy giá trị 0 và 1. -Đại số boolean còn gọi là đại số chuyển mạch (switching algebra) Logic 0 Logic 1 Sai Đúng Tắt Mở Thấp Cao Không Có Công tắc mở Công tắc đóng Khoa KTMT Vũ Đức Lung 9 Tên Dạng AND Dạng OR Định luật thống nhất 1A = A 0 + A = A Định luật không OA = O 1+ A = 1 Định luật Idempotent AA = A A + A = A Định luật nghịch đảo Định luật giao hoán AB = BA A + B = B + A Định luật kết hợp (AB)C = A(BC) (A+B)+C = A + (B+C) Định luật phân bố A + BC = (A + B)(A + C) A(B+C) = AB + AC Định luật hấp thụ A(A + B) = A A + AB = A Định luật De Morgan 0AA 1AA BAAB BABA 4.1.2. Đại số Boolean (Boolean Algebra) Khoa KTMT Vũ Đức Lung 10 4.1.2. Đại số Boolean (Boolean Algebra) Quy tắc về phủ định: Hàm Logic: Bảng chân trị (truth table) XX BABORAy A B y 0 0 0 0 1 1 1 0 1 1 1 1 Khoa KTMT Vũ Đức Lung 11 Phép toán OR và cổng OR Bảng chân trị (truth table), ký hiệu phép toán, ký hiệu cổng Phép toán cho 3 biến, 4 biến, Phép toán AND, NOT, XOR A B x=A+B 0 0 0 0 1 1 1 0 1 1 1 1 A B x Khoa KTMT Vũ Đức Lung 12 Phép toán OR và cổng OR Biểu đồ (Sơ đồ) thời gian. VD: A B x Khoa KTMT Vũ Đức Lung 13 4.1.2. Đại số Boolean (Boolean Algebra) Phép toán AND với cổng AND Phép toán INVerter (NOT) với cổng NOT Phép toán XOR với cổng XOR Ví dụ: – Xác định đầu ra x từ cổng AND, nếu các tín hiệu đầu vào có dạng hình 4.4: Hàm của n biến logic sẽ có 2n tổ hợp biến, Khoa KTMT Vũ Đức Lung 14 4.1.2. Đại số Boolean (Boolean Algebra) Định lý DeMorgan Dạng tổng quát: Ví dụ: BAAB ABBA nn nn xxxxxx xxxxxx ...... ....... 2121 2121 Khoa KTMT Vũ Đức Lung 15 4.1.2. Đại số Boolean (Boolean Algebra) Các cổng tương đương từ định lý DeMorgan Khoa KTMT Vũ Đức Lung 16 4.1.2. Đại số Boolean (Boolean Algebra) Một số ví dụ: – Đơn giản hàm Boolean – Đơn giản mạch – Thiết kế mạch B C F A 3 AND2 8 NOT 9 NOT 2 AND3 4 OR3 1 AND3 CACABABCF Đơn giản??? Khoa KTMT Vũ Đức Lung 17 4.1.2. Đại số Boolean (Boolean Algebra) Ví dụ 1: Dùng bảng chân trị để biểu diễn hàm f = (A AND B) OR (C AND NOT B), vẽ sơ đồ mạch cho hàm f. Ví dụ 2: Dùng Boolean Algebra đơn giản các biểu thức sau: a) y = A + AB b) y = A B D + A DB c) x = ))(( BABA d) ))(( DCBADACBz Khoa KTMT Vũ Đức Lung 18 4.1.2. Đại số Boolean (Boolean Algebra) Ví dụ 3: Để làm một bộ báo hiệu cho lái xe biết một số điều kiện, người ta thiết kế 1 mạch báo động như sau: Tín hiệu từ : Cửa lái: 1- cửa mở, 0 – cửa đóng; B ộ p h ậ n đ á n h l ử a : 1 – b ậ t , 0 – t ắ t ; Đèn pha: 1 – b ậ t , 0 – t ắ t . Mạch Logic Cửa lái Bộ phận đánh lửa Đèn pha Báo động Khoa KTMT Vũ Đức Lung 19 4.2. Bản đồ Karnaugh B A 0 1 0 0 1 1 2 3 BC A 00 01 11 10 0 0 1 3 2 1 4 5 7 6 a) Bản đồ 2 biến b) Bản đồ 3 biến Khái niệm: - Ô kế cận - Các vòng gom chung - Ô không xác định hay tùy định khi gom 2n Ô kế cận sẽ loại được n biến. Những biến bị loại là những biến khi ta đi vòng qua các ô kế cận mà giá trị của chúng thay đổi. f(A,B,C) = )6,5,4,2,0( Khoa KTMT Vũ Đức Lung 20 4.2. Bản đồ Karnaugh Những điều cần lưu ý: – Vòng gom được gọi là hợp lệ – biểu diễn hàm Boolean theo dạng tổng các tích (dạng 1) hay theo dạng tích các tổng (dạng 2) – Các vòng phải được gom sao cho số ô có thể vào trong vòng là lớn nhất và nhớ là để đạt được điều đó, thường ta phải gom cả những ô đã gom vào trong các vòng khác Khoa KTMT Vũ Đức Lung 21 4.2. Bản đồ Karnaugh CD AB 00 01 11 10 00 0 1 3 2 01 4 5 7 6 11 12 13 15 14 10 8 9 11 10 c) Bản đồ 4 biến Khoa KTMT Vũ Đức Lung 22 4.2. Bản đồ Karnaugh Ví dụ 1: Dùng bản đồ Karnaugh đơn giản hàm f(A,B,C) = Ví dụ 2: Dùng bản đồ Karnaugh rút gọn hàm và vẽ sơ đồ mạch của hàm f dùng các cổng AND, OR và NOT. Ví dụ 3: Ví dụ 4: Cực tiểu các hàm trên ở dạng tích các tổng )6,5,4,2,0( )13,12,9,7,6,4,3,2,0(),,,( DCBAf )13,11,10,9,8,7,6,4,3,2,1,0(),,,( DCBAf Khoa KTMT Vũ Đức Lung 23 4.3. Những mạch logic số cơ bản Mạch tích hợp IC (Intergrated Circuit) Mạch kết hợp (Combinational circuit) Mạch Giải Mã & Mã Hóa Mạch Tuần Tự • Mạch số là mạch điện tử hoạt động ở hai mức cao và thấp. Thường biểu diễn trạng thái cao là 1, trạng thái thấp là 0. Khoa KTMT Vũ Đức Lung 24 Mạch SSI (cỡ nhỏ): 1-10 cổng Mạch MSI (trung bình): 10-100 cổng Mạch LSI (cỡ lớn): 100-100.000 cổng Mạch VLSI (rất lớn): > 100.000 cổng Mạch Tích hợp Các linh kiện điện tử được gắn trên cùng một bản mạch và nối với nhau thông qua các đường khắc dẫn tín hiệu trên bản mạch này. Các mạch này ngày càng thu nhỏ lại gọi là mạch tích hợp – Integrated circuit (IC) IC được chia thành các loại dưới đây tùy thuộc vào khả năng chứa và sắp xếp các cổng trên cùng một chip gọi là mức tích hợp: Mạch Tích hợp IC (Intergrated Circuit) Khoa KTMT Vũ Đức Lung 25 Một số vi mạch SSI Khoa KTMT Vũ Đức Lung 26 CHIP Các IC được nén lại và đóng gói vào trong 1 vỏ bọc bằng gốm (Ceramic), hoặc chất dẻo có các chân ra ngoài gọi là CHIP. Khoa KTMT Vũ Đức Lung 27 Các kiểu đóng gói CHIP Dual Inline Package (DIP) Pin Grid Array (PGA) Plastic Quad Flat Pack Khoa KTMT Vũ Đức Lung 28 Mạch kết hợp (tổ hợp) (Combinational circuit) 1. Định nghĩa Mạch kết hợp là tổ hợp các cổng luận lý kết nối với nhau tạo thành một bản mạch có chung một tập các ngõ vào và ra. Khoa KTMT Vũ Đức Lung 29 2. Các bước thiết kế mạch kết hợp 1. Xác định bài toán để đi đến kết luận có những đầu nhập, xuất nào 2. Lập bảng chân trị xác định mối quan hệ giữa nhập và xuất 3. Dựa vào bảng chân trị, xác định hàm cho từng ngõ ra 4. Dùng đại số boolean hoặc bản đồ Karnaugh để đơn giản các hàm ngõ ra 5. Vẽ sơ đồ mạch theo các hàm đã đơn giản. Combinational circuit Khoa KTMT Vũ Đức Lung 30 Bộ dồn kênh (Multiplexer) Bộ dồn kênh hay còn gọi là mạch chọn kênh là mạch có chức năng chọn lần lượt 1 trong N kênh vào để đưa đến ngõ ra duy nhất c1 c2 y 0 0 x1 0 1 x2 1 0 x3 1 1 x4 Khoa KTMT Vũ Đức Lung 31 Bộ dồn kênh (Multiplexer) Sơ đồ bộ dồn kênh 4 đầu vào, 1 đầu ra c1 c2 x4 x3 x2 x1 y 6N O T 7N O T 43DNA 33DNA 54RO 23DNA 13DNA Khoa KTMT Vũ Đức Lung 32 Bộ dồn kênh (Multiplexer) 8 đầu vào Khoa KTMT Vũ Đức Lung 33 Bộ phân kênh (Demultiplexer) Khoa KTMT Vũ Đức Lung 34 Mạch cộng (adder) Bảng chân trị và mạch cho bộ nửa cộng bộ nửa cộng (half adder) A B Sum Carry 0 0 0 0 0 1 1 0 1 0 1 0 1 1 0 1 B Carry A Sum 2 AND2 1 XOR Khoa KTMT Vũ Đức Lung 35 Mạch cộng (adder) Bộ cộng đầy đủ(Full Adder) Khoa KTMT Vũ Đức Lung 36 Bộ cộng n bit Khoa KTMT Vũ Đức Lung 37 Mạch giải mã và mã hóa Mạch mã hoá (Encoder) x7 x6 x5 x4 x3 x2 x1 x0 A2 A1 A0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 1 0 0 0 0 1 1 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 1 0 1 0 1 0 0 0 0 0 0 1 1 0 1 0 0 0 0 0 0 0 1 1 1 2n ngõ nhập n ngõ xuất Khoa KTMT Vũ Đức Lung 38 Mạch giải mã và mã hóa Phương trình logic tối giản: A0 = x1 + x3 + x5 + x7 A1 = x2 + x3 + x6 + x7 A2 = x4 + x5 + x6 + x7 ENCODER 83 Khoa KTMT Vũ Đức Lung 39 Mạch giải mã (Decoder) n ngõ nhập 2n ngõ xuất Nếu ngõ nhập có một số tổ hợp không dùng thì số ngõ ra có thể ít hơn 2n . Khi đó mạch giải mã gọi là mạch giải mã n-m, với n m 2 . Khoa KTMT Vũ Đức Lung 40 Mạch giải mã (Decoder) phương trình logic tối giản ABy BAy BAy BAy 3 2 1 0 U1 AND2 1 2 3 U2 AND2 1 2 3 U3 AND2 1 2 3 U4 AND2 1 2 3 U5 INV U6 INV AB y0 y1 y2 y3 Khoa KTMT Vũ Đức Lung 41 3.2.Mạch Giải Mã & Mã Hóa Mạch giải mã 3-8 A B C D0 D1 D2 D3 D4 D5 D6 D7 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 1 1 0 0 0 1 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 1 0 1 0 0 0 0 0 1 0 0 1 1 0 0 0 0 0 0 0 1 0 1 1 1 0 0 0 0 0 0 0 1 Khoa KTMT Vũ Đức Lung 42 Sơ đồ mạch giải mã 3-8 Khoa KTMT Vũ Đức Lung 43 2. Mạch giải mã dùng cổng NAND U 4 I N V U 4 I N V U 4 I N V U 10 N A N D 3 U 11 N A N D 3 U 12 N A N D 3 U 13 N A N D 3 A 0 A 1 E D 0 D 1 D 2 D 3 Mạch giải mã 2-4 với cổng NAND E A1 A0 D0 D1 D2 D3 0 0 0 0 1 1 1 0 0 1 1 0 1 1 0 1 0 1 1 0 1 0 1 1 1 1 1 0 1 x x 1 1 1 1 Khoa KTMT Vũ Đức Lung 44 Trong trường hợp cần mạch giải mã với kích cỡ lớn ta có thể ghép 2 hay nhiều mạch nhỏ hơn lại để được mạch cần thiết Ký hiệu Decoder 24 Mở rộng mạch giải mã
File đính kèm:
 bai_giang_kien_truc_may_tinh_1_chuong_4_mach_logic_so_vu_duc.pdf
bai_giang_kien_truc_may_tinh_1_chuong_4_mach_logic_so_vu_duc.pdf

