Bài giảng Kiểm thử phần mềm - Chương 3: Kiểm thử hộp trắng - Nguyễn Thanh Hùng
Giới thiệu về kiểm thử hộp trắng
Các kỹ thuật kiểm thử hộp trắng:
Kiểm thử đường dẫn cơ sở
Kiểm thử điều kiện/kiểm thử nhánh
Kiểm thử vòng lặp
Kiểm thử luồng điều khiểnNhắc lại: Kiểm thử hộp đen
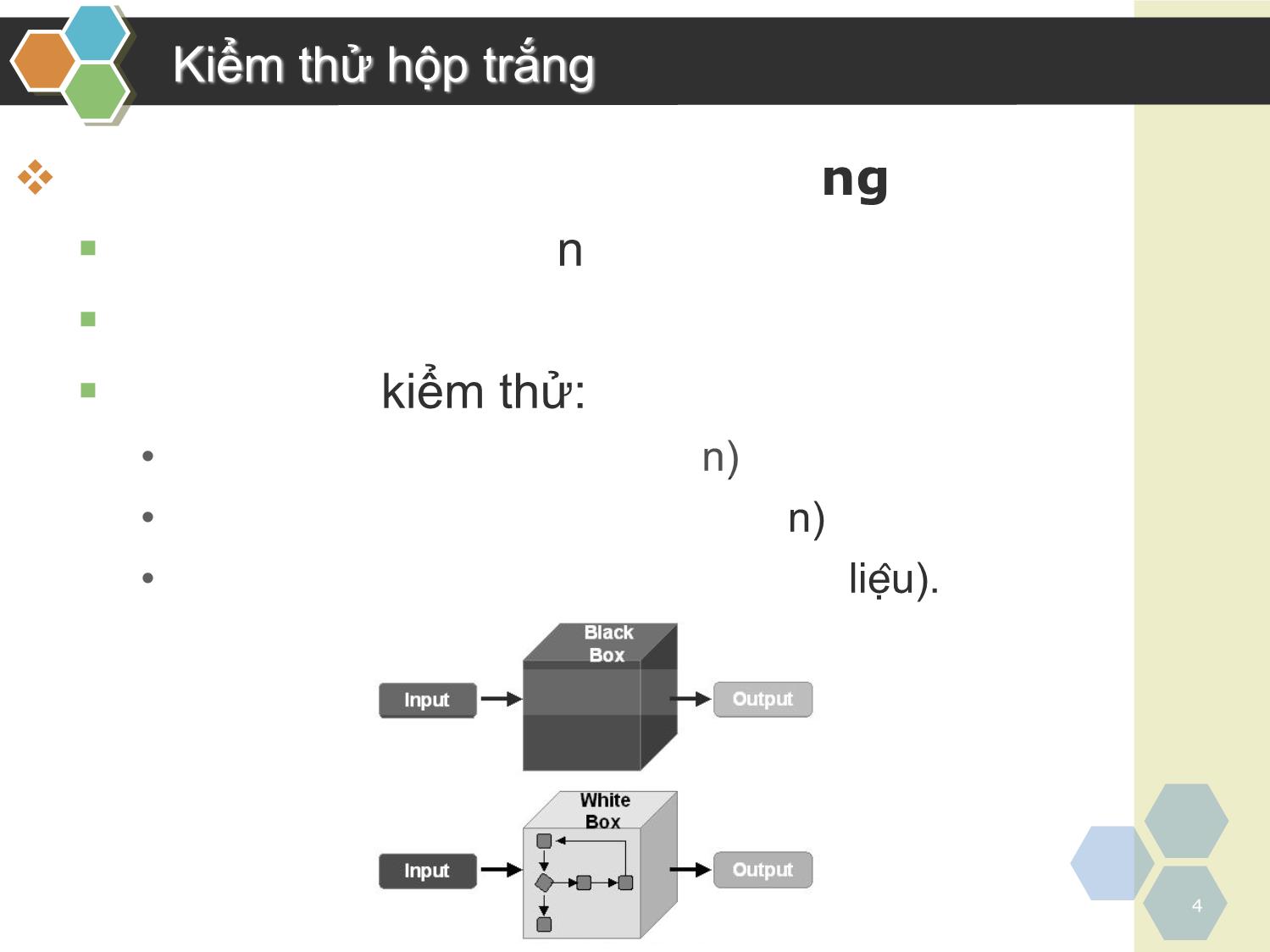
Kiểm thử hộp đen là kiểm thử bỏ qua
cấu trúc bên trong, chỉ quan tâm tới
Output từ Input cho trước có chính xác
không.
Phân loại:
Kiểm thử biên
Kiểm thử lớp tương tương
Bảng quyết định
Kiểm thử đoán lỗi

Trang 1

Trang 2

Trang 3
Trang 4

Trang 5

Trang 6

Trang 7

Trang 8

Trang 9
Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Kiểm thử phần mềm - Chương 3: Kiểm thử hộp trắng - Nguyễn Thanh Hùng", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Kiểm thử phần mềm - Chương 3: Kiểm thử hộp trắng - Nguyễn Thanh Hùng

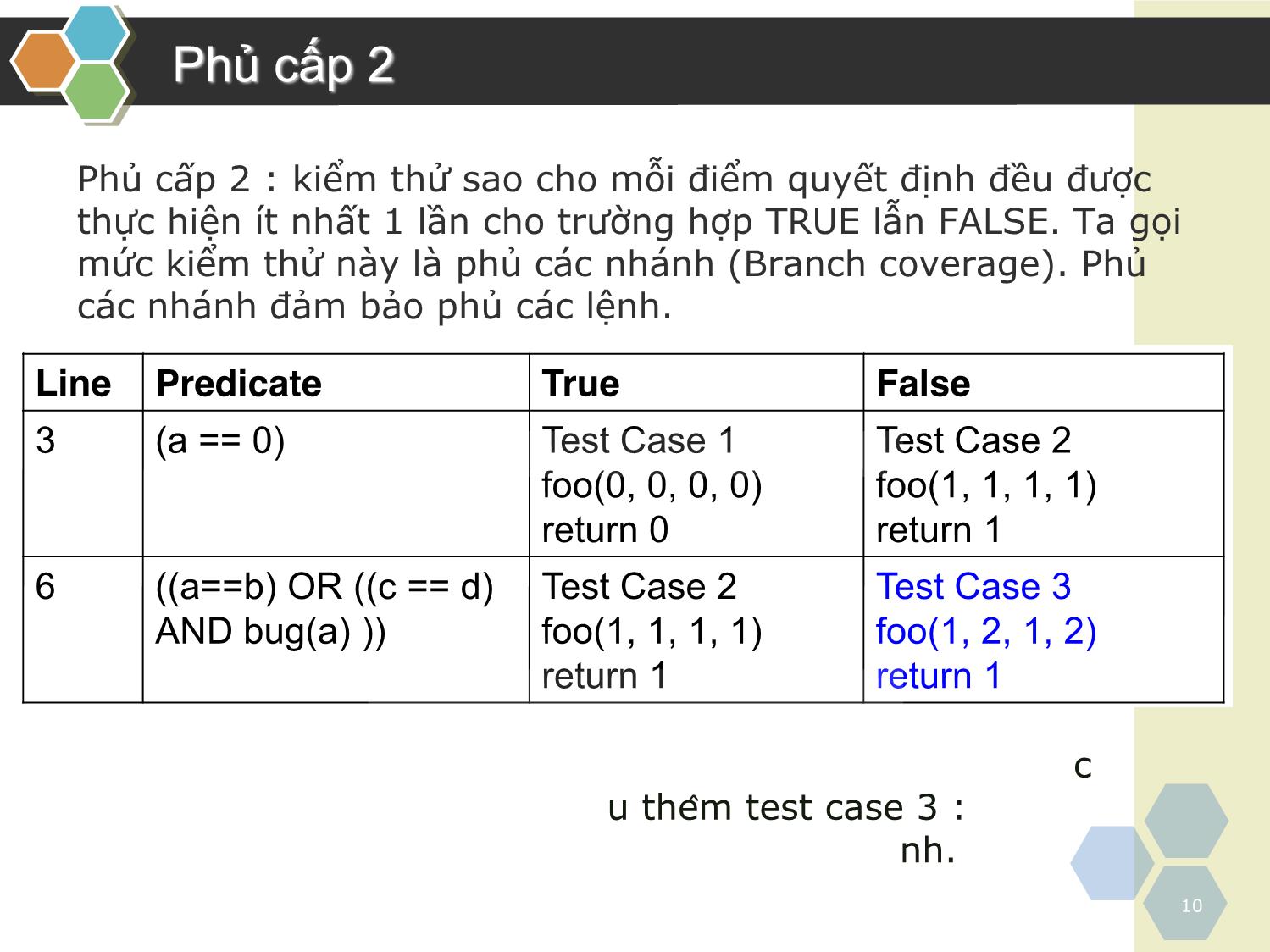
iều khiển
Lưu ý
Không thể có được tất cả các test case
mong muốn bằng việc áp dụng 1 kỹ thuật
kiểm thử duy nhất.
Trước khi áp dụng các kỹ thuật kiểm thử hộp
trắng, hãy xem lại code.
Nội dung
Giới thiệu về kiểm thử hộp trắng
Các kỹ thuật kiểm thử hộp trắng:
. Kiểm thử đường dẫn cơ sở
. Kiểm thử điều kiện/kiểm thử nhánh
. Kiểm thử vòng lặp
. Kiểm thử luồng điều khiển
Kiểm thử đường cơ sở (Basis Path)
Định nghĩa: Thu được các trường hợp thử
nghiệm từ đường cơ sở, được xác định
theo biểu đồ dòng chảy của chương trình
Các bước:
. 1. Xây dựng một đồ thị dòng chảy dựa trên logic của
chương trình
. 2. Tính toán độ phức tạp Cyclomatic của đồ thì dòng chảy
. 3. Xác định đường cơ sở.
. 4. Kiểm tra nếu số đường cơ sở không nhiều hơn độ phức
tạp Cyclomatic.
. 5. Thiết kế trường hợp thử nghiệm để kiểm tra các đường
cơ sở
ng
ng
.
nh.
.
nh.
.
ch:
•
•
19
ng
m:
.
n.
.
n,
ng:
. n.
.
c cung.
20
ng
ng:
Các cấu trúc điều khiển
21
nh
u
a một
nh
22
ng
23
m:
. :
. )
. 11 cung
. n
24
Ví dụ 2
25
nh
t một lệnh).
nh
n hơn).
26
nh
ch sau:
. V(G) = E - N + 2 (= 11-9+2 = 4)
. ng (= 4)
. V(G) = P – 1 (= 5-1 =4)
.
: V(G) = 4
.
27
Quy trình xác định các đường tuyến tính độc lập
c :
t.
i.
i.
a.
C).
28
c nh c ca m thư
29
Ví dụ
30
Độ phức tạp Cyclomatic C
nh
p C = 5+1 = 6.
:
11 ﰂ10 ﰂ 2 ﰂ 1 .1
11 ﰂ10 ﰂ3 ﰂ 2 ﰂ1 .2
12 ﰂ10 ﰂ 2 ﰂ1 .3
9 ﰂ8 ﰂ5 ﰂ4 ﰂ3 ﰂ 2 ﰂ1 .4
9 ﰂ8 ﰂ6 ﰂ5 ﰂ4 ﰂ3 ﰂ 2 ﰂ1 .5
9 ﰂ8 ﰂ7 ﰂ6 ﰂ5 ﰂ4 ﰂ3 ﰂ 2 ﰂ1 .6
31
Thiết kế các test-cases
ng 1:
-
-
a k
ng 4 hay 5 hay 6.
ng 2:
ﰂ i -
p lệ. (2) tcnt = 100. (3) vcnt = 100
ng 3:
-
ng : (1) average = -999. (2) tcnt = 0 (3) vcnt = 0
32
Thiết kế các test-cases
ng 4:
i -999
i k < i
p lệ)
ng 5:
i <= 100 ﰂ i -
i k <= i
p lệ)
ng 6:
ﰂ i -
i<=100
33
p lệ. (2) tcnt3 )= vcnt 100 .= ( 100
Ví dụ
Xét ví dụ về tam giác:
1. program triangle (input, output);
2. VAR a,b,c: integer;
3. IsATriangle: boolean;
4. BEGIN
5. writeln(“Enter integers: “);
6. readln(a,b,c);
7. Writeln(“Side A is: “, a, “Side B is: “, b, “Side C is: “, c);
8. IF(a <b+c) AND (b < a+c) AND (c<a+b) THEN
9. IsATriangle = True;
10. ELSE IsATriangle = False;
11. IF IsATriangle)
12. THEN
13. BEGIN
14. IF (a=b) XOR (a=c) XOR (b=c) AND NOT((a=b) AND (a=c)
15. THEN writeln(“Equilateral”);
16. IF (a=b) AND (b=c)
17. THEN writeln(“Equilateral”);
18. IF(a b) AND (a c) AND (ac)
19. THEN writeln(“Scalene”);
20. END
21. ELSE Writeln(“Not a Triangle”);
22. END
Ví dụ
Thiết kế trường hợp kiểm thử cho kiểm thử đường cơ sở
35
Ví dụ
36
Đồ thị dòng chảy
37
Độ phức tạp “Cyclomatic”
Số vùng khép kín bao gồm cả các hình
tứ giác = 4 +1
Số lượng nhị phân +1 = 4+1=5
Số cạnh – số nút + 2 = 15-12+2=5
Đường cơ sở và các trường hợp kiểm thử (1)
1. 12-15->16->17->21->22->24->26-27->30
Trường hợp kiểm thử: Input = (68,68,56)
Kết quả dự kiến: tam giác cân
2. 12-15->16->17->21->22->24->25->30
Trường hợp kiểm thử: Input = (68,60,56)
Kết quả dự kiến: tam giác không cân
Đường cơ sở và các trường hợp kiểm thử (2)
3. 12-15->16->17->21->22->23->30
Trường hợp kiểm thử: Input = (68,68,68)
Kết quả dự kiến: tam giác đều
4. 12-15->16->18->20->21->28-29->30
Trường hợp kiểm thử: Input = (68,8,56)
Kết quả dự kiến: không phải là tam giác
binarySearch() Example
Bài tập - BinarySearch
public int binarySearch(int sortedArray[ ], int searchValue)
{
int bottom = 0;
int top = sortedArray.length - 1;
int middle, locationOfsearchValue; 2
boolean found = flase;
1 locationOfsearchValue = -1; /* the location of searchValue in the sortedArray */
/* location = -1 means that searchValue is not found */
while ( bottom <= top && !found)
{ 3
middle = (top + bottom)/2;
4 if (searchValue == sortedArray[ middle ])
{
5 found = true;
locationOfsearchValue = middle;
}
6 else if (searchValue < sortedArray[ middle ])
top = middle - 1;
else 7
8 bottom = middle + 1;
} // end while
9
10 return locationOfsearchValue;
}
41
25
The CFG of Function binarySearch()
1
2
3
4
6 5
8 7
9
10 26
13
binarySearch() Example
public int binarySearch(int sortedArray[ ], int searchValue)
{
int bottom = 0;
int top = sortedArray.length - 1;
int middle, locationOfsearchValue; 2
boolean found = flase;
1 locationOfsearchValue = -1; /* the location of searchValue in the sortedArray */
/* location = -1 means that searchValue is not found */
while ( bottom <= top && !found)
{ 3
middle = (top + bottom)/2;
4 if (searchValue == sortedArray[ middle ])
{
5 found = true;
locationOfsearchValue = middle;
}
6 else if (searchValue < sortedArray[ middle ])
top = middle - 1;
else 7
8 bottom = middle + 1;
} // end while
9
10 return locationOfsearchValue;
}
25
Bài tập – BinarySearch - CFG
The CFG of Function binarySearch()
1
2
3
4
6 5
8 7
9
10 26
42
13
Cyclomatic Complexity
• Three ways to compute cyclomatic complexity:
– The number of regions of the flow graph correspond
to the cyclomatic complexity.
– Cyclomatic complexity, V(G), for a flow graph G is
defined as V(G) = E - N + 2 (13-10+2=5)
where E is the number of flow graph edges and N is
the number of flow graph nodes.
– Cyclomatic complexity, V(G) = P + 1
where P is the number of predicate nodes contained
in the flow graph G.
29
CyclomatBàiic tậpCo –mBinarySearchplexity o f– FĐộu nphứccti otạpn
binarySearch()
1 predicate nodes
2
3
R3 4
R1 regions
6 R2 5
8 R5
R4 7
9 V(G) = 5 regions
10 V(G) = 13(edges) – 10(nodes) +2 = 5
V(G) = 4(predicate nodes)30 + 1 = 5
43
15
Cyclomatic Complexity
• Three ways to compute cyclomatic complexity:
– The number of regions of the flow graph correspond
to the cyclomatic complexity.
– Cyclomatic complexity, V(G), for a flow graph G is
defined as V(G) = E - N + 2 (13-10+2=5)
where E is the number of flow graph edges and N is
the number of flow graph nodes.
– Cyclomatic complexity, V(G) = P + 1
where P is the number of predicate nodes contained
in the flow graph G.
29
CyclomatBàiic tậpCo –mBinarySearchplexity o f– FĐườngunct icơo nsở
binarySearch()
1 predicate nodes
2
3
R3 4
R1 regions
6 R2 5
8 R5
R4 7
9 Path 1: 1-2-10
Path 2: 1-2-3-10
10 Path 3: 1-2-3-4-5-9-2- ...
Path 4: 1-2-3-4-6-7-9-230-...
Path 5: 1-2-3-4-6-8-9-2-... 44
15
Bài tập – BinarySearch – Test-cases
Path 1 test case:
. Inputs: sortedArray = { }, searchValue = 2
. Expected results: locationOfSearchValue = -1
Path 2 test case: cannot be tested stand-alone!
. Inputs: sortedArray = {2, 4, 6}, searchValue = 8
. Expected results: locationOfSearchValue = -1
Path 3 test case:
. Inputs: sortedArray={2,4,6,8,10},searchValue = 6
. Expected results: locationOfSearchValue = 2
• Path 4 test case:
. Inputs: sortedArray = {2, 4, 6, 8, 10}, searchValue = 4
. Expected results: locationOfSearchValue = 1
• Path 5 test case:
. Inputs: sortedArray = {2, 4, 6, 8, 10}, searchValue = 10
. Expected results: locationOfSearchValue = 4 45
Kỹ thuật ma trận kiểm thử
ng:
. t
. t cột.
t
46
Ví dụ ma trận kiểm thử
47
Ví dụ ma trận kiểm thử
2 – 1 = 1
2 – 1 = 1
1 – 1 = 0
2 – 1 = 1
1 – 1 = 0
1 – 1 = 0
1 – 1 = 0
V(G) = 3 + 1 = 4
48
Nội dung
Giới thiệu về kiểm thử hộp trắng
Các kỹ thuật kiểm thử hộp trắng:
. Kiểm thử đường dẫn cơ sở
. Kiểm thử điều kiện/kiểm thử nhánh
. Kiểm thử vòng lặp
. Kiểm thử luồng điều khiển
Kiểm thử điền kiện
Kiểm thử điều kiện
. Phương pháp thiết kế test-case để kiểm tra các điều kiện logic
Điều kiện logic
. u kiện đơn nh): X
. u kiện đơn c
nh: , ≥ hay ≠
c
p
nh (┘)
D = X1 & X2 &...Xn Xi bool
Nếu một điều kiện sai, ít nhất một thành phần trong
điều kiện sai
50
u kiện lôgic
Sai biến Bool
Sai toán tử Bool
Sai số hạng trong biểu thức toán tử Bool
Sai toán tử quan hệ
Sai biểu thức số học
51
nh
u kiện nh.
u kiện t hiện
nh liên quan.
nh
nh “true” “false”
n.
52
n
n
cho c
a.
i, song c hiện!
c
nh n (quan hệ)
?
53
BRO
BRO quan hệ
(branch and relational operation)
. ng “
n thư”
n chung.
. :
D=X1&X2&...Xn, Xi bool
a Xi
nh?.
54
– o
ng buộc Xi u kiện D
,
u kiện đơn Xi trong
ng.
: Khi
cho c
i Xi
n để a D
55
– ng buộc
i n Bool B
t (true) hoặc f (false).
c quan hệ (AΘB
quan hệ:
>, <, =, #
c).
56
– ng buộc 1
u kiện C = A ∩ B
n Bool
u ra a f.
ng buộc
a C.
. i C=t
. i C=f
57
– ng buộc
u kiện C=(B=E)
“=“ “”
i f
c cặp (t,t), (t,f) (f,t)
i “=“
i “”
:
(f,=)
quan hệ trong
C
58
– ng buộc
u kiện c
quan hệ (A>B) (E=F)
ng buộc (f,t)
: (>,=); (>,,>);
(=,=) (<,=).
quan hệ trong
C.
59
Nội dung
Giới thiệu về kiểm thử hộp trắng
Kiểm thử đường dẫn cơ sở
Kiểm thử điều kiện/kiểm thử nhánh
Kiểm thử vòng lặp
Kiểm thử luồng điều khiển
Kiểm thử vòng lặp
Định nghĩa:
Tập trung vào hiệu lực của các cấu trúc vòng lặp, đặc biệt là
các biến thể vòng lặp.
Bốn kiểu vòng lặp:
. 1. Simple loop: một vòng lặp đơn
. 2. Nested loops: một vòng lặp trong vòng lặp khác
. 3. Concatenated loops: một vòng lặp sau vòng lặp khác
. 4. Unstructured loops: các vòng lặp được nối vòng và lồng nhau
phức tạp 61
Kiểm thử vòng lặp
Simple
Loop
Nested
Loops
Concatenated
Loops Unstructured Loops
62
Kiểm thử các vòng lặp đơn
Với n là số vòng lặp tối đa cho
phép, các trường hợp kiểm tra bao
gồm:
1. hoàn toàn bỏ qua vòng lặp
2. qua một vòng lặp
3. qua hai vòng lặp
4. qua m vòng lặp với m < n
5. qua (n-1), n, và (n+1) vòng lặp
63
Kiểm thử vòng lặp lồng nhau
1. Bắt đầu vòng lặp trong cùng. Đặt tất
cả các vòng ngoài với các giá trị tham
số tối thiểu cho sự lặp lại của chúng.
2. Kiểm tra các giá trị tối thiểu, điển hình,
tối đa cho vòng lặp trong cùng, trong
khi giữ các vòng lặp ngoài tại các giá
Nested trị tối thiểu của chúng.
Loops 3. Di chuyển ra khỏi một vòng lặp và
thiết lập nó như trong bước 2, giữ tất
cả các vòng lặp bên trong những giá
trị tiêu biểu. Tiếp tục bước này cho
đến khi vòng lặp ngoài cùng đã được64
thử nghiệm.
Kiểm thử vòng lặp ghép nối
Nếu mỗi vòng lặp là độc lập với
các vòng lặp khác thì kiểm tra
chúng như các vòng lặp đơn
giản.
Nếu hai vòng được nối tiếp,
vòng lặp 1 được dùng như là giá
Concaten
ated trị ban đầu cho vòng lặp 2 thì
Loops kiểm tra chúng như các vòng lặp
lồng nhau.
65
Nội dung
Giới thiệu về kiểm thử hộp trắng
Kiểm thử đường dẫn cơ sở
Kiểm thử điều kiện/kiểm thử nhánh
Kiểm thử vòng lặp
Kiểm thử luồng điều khiển
Tiêu chuẩn bao phủ
Đôi khi còn được gọi là tiêu chuẩn kiểm thử phần mềm
hoặc tiêu chuẩn kiểm thử dữ liệu đầy đủ có thể được sử
dụng như:
. Quy tắc dừng để xác định tính đầy đủ.
. Kiểm tra đo chất lượng khi mức độ an toàn có liên quan với
mỗi tập kiểm tra.
. Lựa chọn dữ liệu kiểm thử. Bộ kiểm tra được coi là tương
đương nếu đáp ứng các tiêu chí tương tự.
Tiêu chuẩn kiểm thử hộp trắng
• Tiêu chuẩn có xem xét đến cấu trúc bên trong của chương trình
có thể được chia thành.
1. Tiêu chuẩn luồng điều khiển.
2. Tiêu chuẩn luồng dữ liệu.
67
Tiêu chuẩn luồng điều khiển
Tiêu chuẩn luồng điều khiển
. Kiểm tra các biểu thức logic trong đó xác định các
nhánh và cấu trúc vòng lặp của chương trình.
. Được sử dụng chủ yếu trong các ngành công
nghiệp.
. Các tiêu chí phổ biến nhất bao gồm:
• 1. Bao phủ câu lệnh
• 2. Bao phủ quyết định
• 3. Bao phủ điều kiện
• 4. Bao phủ quyết định / điều kiện
• 5. Bao phủ đa điều kiện
68
Thứ tự tiêu chuẩn luồng điều khiển
Định nghĩa
. Nếu tất cả các tập kiểm tra thỏa mãn A cũng đáp ứng
B thì ta nói tiêu chuẩn A mạnh hơn tiêu chuẩn B
Thứ tự các tiêu chuẩn
. Phạm vi tiêu chuẩn bao phủ là yếu nhất.
. Điều kiện tiêu chuẩn bao phủ là mạnh nhất.
. Trình tự giữa cả hai là quyết định phạm vi bao phủ,
điều kiện bao phủ và quyết định phạm vi / điều khiện
bao phủ.
69
Bao phủ câu lệnh
Code1: . Định Nghĩa:
if ((A > 1) && (B == 0)) • Mỗi câu lệnh trong chương
X = X/A; trình được thực hiện ít nhất
if ((A == 2) || (X > 1)) một lần.
X=X+1;
. Ví dụ:
• Để thoả mãn bao phủ câu
Code2: lệnh đáp ứng đoạn Code 1, một
if ((A > 1) || (B == 0)) trường hợp kiểm thử có thể:
X = X/A; A = 2 B= 0 X = 3
if ((A == 2) || (X > 1))
X=X+1; • Như đã thấy, tất cả các câu
lệnh đều được thực thi.
• Nhưng điều gì sẽ xảy ra nếu
code sai như trong Code 2?
70
Bao phủ điều kiện (1)
. Định Nghĩa:
Code1:
if ((A > 1) && (B == 0)) • Mỗi câu lệnh trong chương
X = X/A; trình được thực hiện ít nhất
if ((A == 2) || (X > 1)) một lần và mỗi điều kiện có
X=X+1; thể xảy ra ít nhất một lần.
• Một quyết định là một biểu
thức Boolean bao gồm một
hoặc nhiều điều kiện kết hợp
bởi các từ nối hợp lí, chẳng
hạn như “AND”, “OR” và
“NOT”.
71
Bao phủ điều kiện (2)
. Ví dụ:
• Để thoả mãn bao phủ điều
Code1: kiện đáp ứng đoạn code 1,
if ((A > 1) && (B == 0)) một trường hợp kiểm thử có
X = X/A; thể:
if ((A == 2) || (X > 1)) A = 2 B= 0 X = 2
X=X+1;
A = 1 B= 0 X = 1
Code2: • Như đã thấy, tất cả các
if ((A > 1) && (B >= 0)) câu lệnh đều được thực thi.
X = X/A;
if ((A == 2) || (X > 1)) • Nhưng điều gì sẽ xảy ra
X=X+1; nếu code sai trong ví dụ 2?
72
Áp dụng kỹ thuật kiểm thử hộp trắng
Dưới đây là một phương thức của một lớp nào đó, hãy áp
dụng kiểm thử hộp trắng để lấy được trường hợp kiểm thử
của nó
73
Trả lời
Để áp dụng kiểm thử hộp trắng để lấy được
các trường hợp kiểm thử của nó, có thể làm
như sau:
. Bước 1: Rút ra các trường hợp kiểm thử từ kiểm thử
đường dẫn cơ sở.
. Bước 2: Rút ra các trường hợp kiểm thử từ các kiểm
thử rẽ nhánh.
. Bước 3: Rút ra các trường hợp kiểm thử từ kiểm thử
vòng lặp.
. Bước 4: Cuối cùng nên thiết lập kiểm thử kết hợp tất
cả các bước trên.
. Bước 5: Bổ xung các trường hợp kiểm thử đặc biệt
theo tính năng của chương trình.
74
Tóm tắt
Kĩ thuật kiểm thử hộp trắng có thể kiểm tra logic
của chương trình dựa trên cấu trúc của nó.
Kĩ thuật kiểm thử hộp trắng bao gồm thử nghiệm
đường dẫn cơ sở, kiểm tra rẽ nhánh và kiểm thử
vòng lặp.
Tiêu chuẩn bao phủ có thể được sử dụng như quy
tắc dừng và kiểm tra dữ liệu.
Tiêu chuẩn luồng điểu khiển được áp dụng trong
các ngành công nghiệp bao gồm bao phủ câu
lệnh, bao phủ điều kiện, bao phủ quyết định /
điều kiện và bao phủ đa điều kiện.
75
THE END
76File đính kèm:
 bai_giang_kiem_thu_phan_mem_chuong_3_kiem_thu_hop_trang_nguy.pdf
bai_giang_kiem_thu_phan_mem_chuong_3_kiem_thu_hop_trang_nguy.pdf

