Bài giảng Khoa học máy tính - Chuẩn bị toán học - Nguyễn Phương Thái

Trang 29
Lý thuyết Thông tin - Khoa Công Nghệ Thông Tin
Bài 3 Chuẩn bị toán học
3.1 Xác suất (Probability)
3.2 Bất đẳng thức Chebyshev và luật yếu của số lớn
3.3 Tập lồi (Convex sets) và hàm lồi (convex functions), bất 
đẳng thức Jensen
3.4 Công thức Stirling
Trang 30
Lý thuyết Thông tin - Khoa Công Nghệ Thông Tin
Xác suất
„ Không gian mẫu (Sample space)
„ Là tập (hay không gian) tất cả các kết quả có thể có của một thí
nghiệm. Thường được kí hiệu là E hay S. Nếu không gian mẫu 
là rời rạc thì E có thể được biểu diễn bằng E = {e1, e2, ..., en}
„ Sự kiện (Event), sự kiện cơ bản (elementary event)
„ Mỗi tập con của E (không gian mẫu) được gọi là một sự kiện, 
đặc biệt mỗi phần tử của E được gọi là một sự kiện cơ bản.
„ Ví dụ
„ Trong một thí nghiệm tung đồng xu thì E = {U (úp), N (ngửa)}. 
Nếu đồng tiền là đồng nhất thì xác suất P(U) = P(N) = 1/2.
„ Trong một thí nghiệm tung con xúc xắc thì E = {1, 2, 3, 4, 5, 
6}. Nếu con xúc xắc là đồng nhất thì xác suất P(1) = P(2) = 
P(3) = P(4) = P(5) = P(6) = 1/6, P(2, 5) = 1/3, P(1, 3, 5) = 1/2.
Trang 31
Lý thuyết Thông tin - Khoa Công Nghệ Thông Tin
Xác suất (tt)
„ Lấy một văn bản tiếng Anh điển hình và nhặt một kí tự bất kỳ
thì E = {a, b, c, ..., x, y, z} và xác suất của các kí tự được phân 
bố như sau P(a) = 0,0642 , ..., P(e) = 0,103 , ..., P(z) = 0,0005.
„ Biến ngẫu nhiên rời rạc (Discrete random variable)
„ Một biến ngẫu nhiên rời rạc x được định nghĩa bằng cách gán 
một số thực xi tới mỗi sự kiện cơ bản ei của không gian mẫu rời 
rạc E. Xác suất của xi được định nghĩa là xác suất của sự kiện 
cơ bản tương ứng và được kí hiệu là p(xi).
„ Trị trung bình (kỳ vọng) (average, expected value), 
phương sai (variance)
„ Trị trung bình và phương sai của biến ngẫu nhiên rời rạc x lần 
lượt được kí hiệu và định nghĩa như sau
„ E(x) = ( )∑=
i
ii p xxx
Trang 32
Lý thuyết Thông tin - Khoa Công Nghệ Thông Tin
Xác suất (tt)
„ Var(x) =
=
trong đó E(x2) là trị kỳ vọng của x2.
„ Tổng quát, trị kỳ vọng của một hàm của x, chẳng hạn f(x), được 
định nghĩa bằng
„ Xác suất đồng thời (joint probability), xác suất có điều 
kiện (conditional probability)
„ Một cặp biến ngẫu nhiên (x, y) liên kết với một thí nghiệm tạo 
thành một biến ngẫu nhiên nối (joint random variable). Nếu x, y 
là rời rạc, sự phân bố xác suất nối hay xác suất đồng thời được 
định nghĩa là
pij = P(x = xi, y = yj)
( )( ) ( ) ( )∑ −=−
i
ii pE xxxxx
22
( ) 22 xx −E
( )( ) ( ) ( )∑=
i
ii pffE xxx
Trang 33
Lý thuyết Thông tin - Khoa Công Nghệ Thông Tin
Xác suất (tt)
„ Xác suất của y trong điều kiện đã biết x được gọi là xác suất có 
điều kiện và được định nghĩa là
trong đó xác suất lề (marginal probability) p(xi) được giả thiết 
là khác không.
„ Các xác suất lề được định nghĩa như sau:
p(xi) = 
p(yj) = 
( ) ( )( )i jiij xp
yxp
xyp
,=
( )∑
j
ji yxp ,
( )∑
i
ji yxp ,
Trang 34
Lý thuyết Thông tin - Khoa Công Nghệ Thông Tin
Ví dụ
„ Thí nghiệm tung đồng thời
một đồng xu và con xúc xắc.
„ Từ kết quả trên ta thấy
P(U, 5) = 1/18
P(Đồng xu = U) = 5/9
P(Đồng xu = N) = 4/9
P(Xúc xắc = 5) = 7/72
P(Xúc xắc = 5 đã biết Đồng xu = U)
1/12 1/18
1/9 1/18
1/9 1/6
1/9 1/24
1/18 1/24
1/12 1/12
U N
6
5
4
3
2
1
Xúc xắc
Đồng xu
Trang 35
Lý thuyết Thông tin - Khoa Công Nghệ Thông Tin
Xác suất (tt)
„ Sự độc lập (Independence)
„ Hai biến ngẫu nhiên x và y được gọi là độc lập nếu
p(xi, yj) = p(xi)p(yj) ∀ i, j.
„ Chúng ta thấy nếu hai biến x và y độc lập thì
có nghĩa là xác suất yj trong điều kiện có xi xảy ra hay không 
xảy ra đều như nhau, không thay đổi, và ngược lại.
„ Cũng từ sự độc lập chúng ta suy ra một kết quả mà hay được sử
dụng sau này
E(xy) = E(x) E(y) = 
( ) ( )( ) ( ) ( )( ) ( )ji jii jiij ypxp
ypxp
xp
yxp
xyp === ,
yx
Trang 36
Lý thuyết Thông tin - Khoa Công Nghệ Thông Tin
Xác suất (tt)
„ Sự tương quan (correlation)
„ Sự tương quan C giữa hai biến x và y được định nghĩa là trị kỳ
vọng của (x – )(y – ):
C(x, y) = E((x – )(y – )) = 
= E(xy) – 
„ Trong trường hợp x và y là độc lập chúng ta suy ra C(x, y) = 0. 
Tuy nhiên điều ngược lại thì không đúng.
x y
x y
yx
Trang 37
Lý thuyết Thông tin - Khoa Công Nghệ Thông Tin
Bất đẳng thức Chebyshev
và luật yếu của số lớn
„ Bất đẳng thức Chebyshev
„ Cho một biến ngẫu nhiên x có trị trung bình là và phương sai 
là , bất đẳng thức Chebyshev đối với một số dương tuỳ ý δ là
P(|x – | ≥ δ) ≤
„ Chứng minh
„ Định nghĩa một hàm f(x) như sau
„ Thì
P(|x – | ≥ δ) = Σ f(xi)p(xi)
x
2
xδ
x 2
2
x
δ
δ
( )
⎩⎨
⎧
<
≥=
δ| - ,|
δ| - ,|f
xx0
xx1x
x
Trang 38
Lý thuyết Thông tin - Khoa Công Nghệ Thông Tin
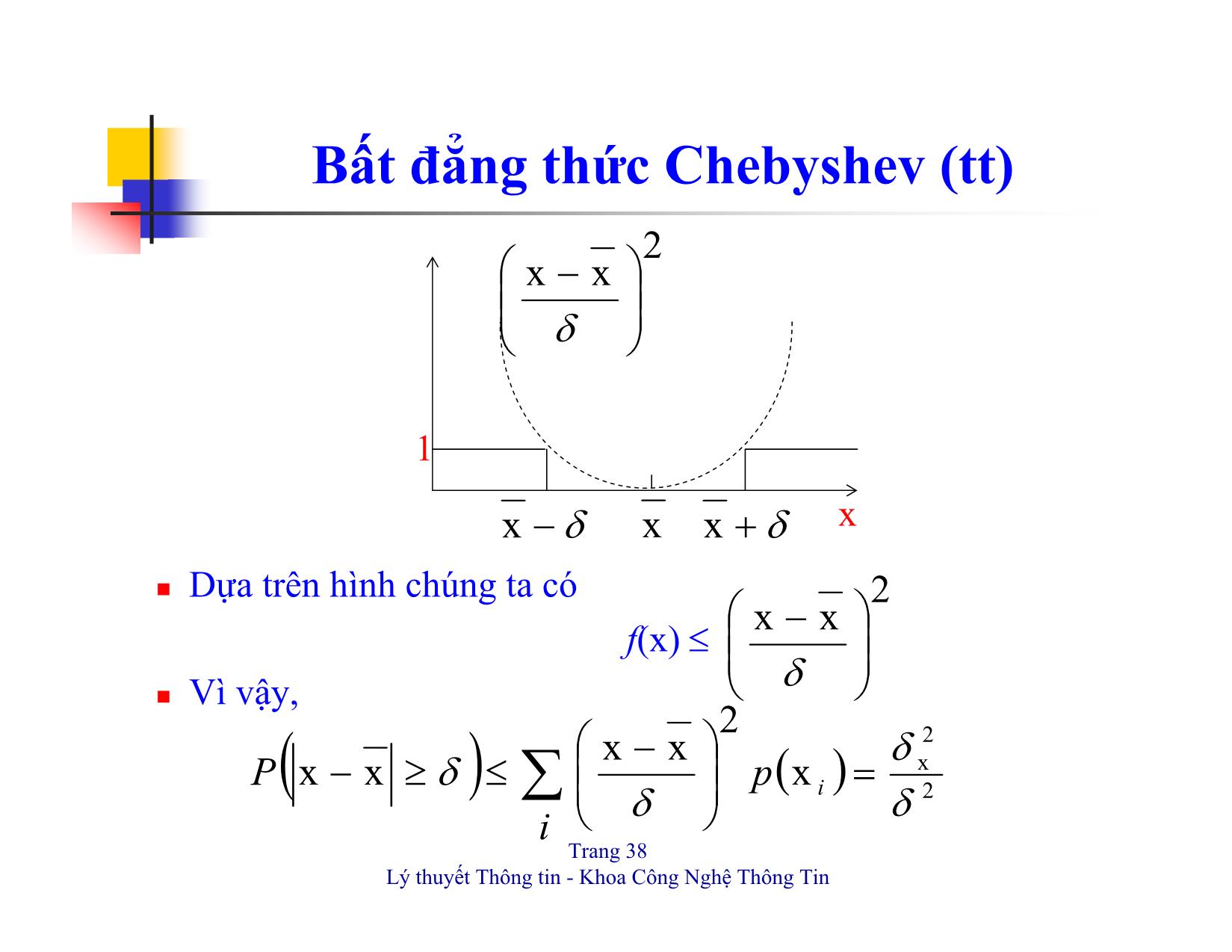
Bất đẳng thức Chebyshev (tt)
„ Dựa trên hình chúng ta có
f(x) ≤
„ Vì vậy,
xδ−x x
1
δ+x
2
xx
⎟⎟⎠
⎞
⎜⎜⎝
⎛ −
δ
2
xx
⎟⎟⎠
⎞
⎜⎜⎝
⎛ −
δ
( ) ( )∑ =⎟⎟⎠⎞⎜⎜⎝⎛ −≤≥− i pP i 2
2
xx
2
xxxx δ
δ
δδ
Trang 39
Lý thuyết Thông tin - Khoa Công Nghệ Thông Tin
Luật yếu của số lớn (tt)
„ Xét một thí nghiệm nhị phân trong đó các kết quả của thí
nghiệm là 0 và 1 với các xác suất tương ứng là p0 và 1– p0.
„ Thí nghiệm này được lặp lại N lần một cách độc lập, và kết quả
trung bình được định nghĩa là yN; tức là, yN bằng tổng số các số
1 trong N lần thí nghiệm chia cho N.
„ Rõ ràng, yN là một biến ngẫu nhiên có không gian mẫu là {0, 
1/N, 2/N, ..., 1}.
„ Định nghĩa x(n) là biến ngẫu nhiên tương ứng với kết quả của 
lần thí nghiệm thứ n, chúng ta có
( )∑
=
=
N
n
n
N N 1
x1y
Trang 40
Lý thuyết Thông tin - Khoa Công Nghệ Thông Tin
Luật yếu của số lớn (tt)
( )( ) xx1x1y
11
∑∑
==
===
N
n
N
n
n
N N
E
N
( )( ) ( ) ⎟⎟⎠⎞⎜⎜⎝⎛ ⎥⎦⎤⎢⎣⎡ −=−= ∑=
2
1
22
y xx
1yy
N
n
n
NN N
EEδ
( )
⎟⎟⎠
⎞
⎜⎜⎝
⎛
⎟⎟⎠
⎞
⎜⎜⎝
⎛
⎥⎦
⎤⎢⎣
⎡ −= ∑
=
2
1
xx1 N
N
E
N
n
n ( )( ) ⎟⎟⎠
⎞
⎜⎜⎝
⎛
⎥⎦
⎤⎢⎣
⎡ −= ∑
=
2
1
2 xx
1 N
n
nE
N
( )( )( )
N
N
N
E
N
N
n
n
2
x2
x2
1
2
2
1xx1 δδ ==−= ∑
=
Trang 41
Lý thuyết Thông tin - Khoa Công Nghệ Thông Tin
Luật yếu của số lớn (tt)
„ Đối với một số nguyên dương tuỳ ý ε, theo bất đẳng thức 
Chebyshev chúng ta có
từ đây chúng ta dẫn ra được luật yếu của số lớn
„ Chú ý rằng vế phải tiến tới 0 khi N tiến ra vô cùng.
„ Luật yếu của số lớn vì vậy khẳng đinh rằng trị trung bình mẫu 
của x tiếp cận trị trung bình thống kê với xác suất cao khi N →
∞.
( ) 22y|yy| εδε ≤≥− NNP
( )
2
2
x
1
xx1 ε
δε
NN
P
N
n
n ≤⎟⎟⎠
⎞
⎜⎜⎝
⎛ ≥−⎥⎦
⎤⎢⎣
⎡ ∑
=
Trang 42
Lý thuyết Thông tin - Khoa Công Nghệ Thông Tin
Tập lồi
„ Trong không gian Ơclit, một tập S được gọi là lồi (convex cap 
(∩)) nếu đối với một cặp điểm P1, P2 thuộc S thì mọi điểm 
thuộc đoạn P1P2 cũng thuộc S.
„ Nếu P1 = (x1, x2, ..., xn) và P2 = (y1, y2, ..., yn) là các điểm trong 
không gian Ơclit n chiều, thì đoạn thẳng nối chúng được biểu 
diễn bằng tập các điểm P, trong đó
P = λP1 + (1–λ)P2
= (λx1 + (1–λ)y1, λx2 + (1–λ)y2, ..., λxn + (1–λ)yn) và λ ∈ [0, 1]. 
(a)
P1
P2
P1
P2
(b)
Trang 43
Lý thuyết Thông tin - Khoa Công Nghệ Thông Tin
Hàm lồi
„ Một ví dụ quan trọng của tập lồi là tập tất cả các điểm (p1, p2, 
..., pn) trong đó (p1, p2, ..., pn) là một sự phân bố xác suất (tức là
các pi ∈ [0, 1] và Σpi = 1).
„ Một hàm thực f(P), được định nghĩa trên tập lồi S, được gọi là
lồi nếu ∀cặp điểm P1, P2 ∈ S, và ∀ λ ∈ [0, 1] bất đẳng thức sau 
đây đúng:
f(λP1 + (1–λ)P2) ≥ λf(P1) + (1–λ)f(P2)
xx1 (λx1 + (1-λ)x2 x2
f(x1)
f(x) f(x2)
f((λx1 + (1-λ)x2)
λf(x1) + (1-λ)f(x2)
Trang 44
Lý thuyết Thông tin - Khoa Công Nghệ Thông Tin
Định lý, bất đẳng thức Jensen
„ Nếu λ1, ..., λN là các số không âm có tổng bằng 1 thì đối với 
mọi tập điểm P1, ..., PN trong miền xác định của hàm lồi f(P) 
bất đẳng thức sau đây đúng
„ Cho biến ngẫu nhiên x lấy các giá trị x1, ..., xn với các xác suất 
p1, ..., pn. Cho f(x) là một hàm lồi có miền xác định chứa x1, ..., 
xn. Chúng ta có E(x) = và E(f(x)) = .
„ Áp dụng định lý trên chúng ta có
f(E(x)) ≥ E(f(x))
Đây được gọi là bất đẳng thức Jensen.
( )∑∑
==
λ≥⎟⎟⎠
⎞
⎜⎜⎝
⎛ λ
N
n
nn
N
n
nn PfPf
11
∑
i
ii xp ( )∑
i
ii xfp
Trang 45
Lý thuyết Thông tin - Khoa Công Nghệ Thông Tin
Bài 4 Lượng tin
4.1 Lượng tin
4.2 Lượng tin trung bình
Vấn đề cơ bản của truyền thông là việc tái sinh tại một điểm hoặc 
chính xác hoặc gần đúng một thông báo được chọn tại một điểm 
khác.
(Claude Shannon 1948)
Trang 46
Lý thuyết Thông tin - Khoa Công Nghệ Thông Tin
Lượng tin
„ Lượng tin (measure of information) dùng để so sánh định lượng 
các tin tức với nhau.
„ Một tin đối với người nhận đều mang hai nội dung, một là 
độ bất ngờ của tin, hai là ý nghĩa của tin.
„ Khía cạnh ngữ nghĩa chỉ có ý nghĩa đối với con người.
„ Khía cạnh quan trọng nằm ở chỗ tin thật sự là một cái được 
chọn từ một tập các tin (tập các khả năng) có thể.
„ Nếu số tin trong tập tin càng nhiều thì sẽ mang lại một “lượng 
tin” càng lớn khi nhận được một tin (giả sử các tin là bình đẳng 
như nhau về khả năng xuất hiện).
„ Để sự truyền tin đạt hiệu quả cao chúng ta không thể đối đãi 
các tin như nhau nếu chúng xuất hiện ít nhiều khác nhau.
Trang 47
Lý thuyết Thông tin - Khoa Công Nghệ Thông Tin
Lượng tin
„ Xét một tin x có xác suất xuất hiện là p(x), thì chúng ta có thể
xem tin này như là một tin trong một tập có 1/p(x) tin với các 
tin có xác suất xuất hiện như nhau.
„ Nếu p(x) càng nhỏ thì 1/p(x) càng lớn và vì vậy “lượng tin” khi 
nhận được tin này cũng sẽ càng lớn.
„ Vậy “lượng tin” của một tin tỉ lệ thuận với số khả năng của một 
tin và tỉ lệ nghịch với xác suất xuất hiện của tin đó.
„ Xác suất xuất hiện của một tin tỉ lệ nghịch với độ bất ngờ khi 
nhận được một tin.
“lượng tin“ ↑ số khả năng ↑ độ bất ngờ ↓ xác suất
„ Một tin có xác suất xuất hiện càng nhỏ thì có độ bất ngờ càng 
lớn và vì vậy có lượng tin càng lớn. 
Trang 48
Lý thuyết Thông tin - Khoa Công Nghệ Thông Tin
Lượng tin (tt)
„ Xét một nguồn A = {a1, a2,, am} với các xác suất xuất hiện là
p(ai) i = 1, ..., m.
„ Kí hiệu lượng tin trong mỗi tin ai là I(ai). Vậy hàm f dùng để
biểu thị lượng tin phải thoã mãn những điều kiện gì?
„ Phản ánh được các tính chất thống kê của tin tức.
„ Ví dụ có hai nguồn K, L với số tin tương ứng là k, l (giả thuyết đều là 
đẳng xác suất). Nếu k > l, thì độ bất ngờ khi nhận một tin bất kỳ của 
nguồn K phải lớn hơn độ bất ngờ khi nhận một tin bất kỳ của nguồn L, 
vậy f(k) > f(l)
„ Hợp lý trong tính toán.
„ Giả thiết hai nguồn độc lập K và L với số tin tương ứng là k và l. Cho 
việc nhận một cặp ki và lj bất kỳ đồng thời là một tin của nguồn hỗn hợp 
KL. Số cặp kilj mà nguồn này có là k*l.
Trang 49
Lý thuyết Thông tin - Khoa Công Nghệ Thông Tin
Lượng tin (tt)
„ Độ bất ngờ khi nhận được một cặp như vậy phải bằng tổng lượng tin của 
khi nhận được ki và lj. Vì vậy chúng ta phải có:
f(kl) = f(k) + f(l)
„ Khi nguồn chỉ có một tin, lượng tin chứa trong tin duy nhất đó
phải bằng không.
f(1) = 0
„ Định nghĩa
„ Lượng đo thông tin của một tin được đo bằng logarit của độ bất 
ngờ của tin hay nghịch đảo xác suất xuất hiện của tin đó.
( ) )(log
)(
1log xp
xp
xI −==
Trang 50
Lý thuyết Thông tin - Khoa Công Nghệ Thông Tin
Lượng tin (tt)
„ Lượng tin chứa trong một dãy x = a1a2  an với ai ∈ A là
„ Trong trường hợp m kí hiệu của nguồn đẳng xác suất với nhau 
tức p(ai) = 1/m thì
Nếu x = a1a2  an với ai ∈ A
I(x) = n logm
( ) ∑
=
−==
n
i
iapxp
xI
1
)(log
)(
1log
( ) m
ap
aI
i
i log)(
1log ==
Trang 51
Lý thuyết Thông tin - Khoa Công Nghệ Thông Tin
Lượng tin trung bình
„ Đơn vị của lượng tin
„ Nếu cơ số là 2 thì đơn vị là bits (cho các kí số nhị phân); nếu cơ 
số là e thì đơn vị là nats (cho đơn vị tự nhiên), nếu cơ số là 10 
thì đơn vị là Hartley.
„ Định nghĩa
„ Lượng tin trung bình của một nguồn tin A là lượng tin trung 
bình chứa trong một kí hiệu bất kỳ của nguồn tin. Nó thường 
được kí hiệu là I(A) và được tính bằng công thức sau
∑∑
∈
−=
∈
=
Aa
apap
Aa
aIapAI
i
ii
i
ii )(log)()()()(
Trang 52
Lý thuyết Thông tin - Khoa Công Nghệ Thông Tin
Ví dụ
„ Cho một nguồn tin U bao gồm 8 tin U = {u0, u1, u2, u3, u4, u5, 
u6, u7}, với các xác suất xuất hiện như sau:
Hãy cho biết lượng tin riêng của mỗi tin và lượng tin trung bình 
của nguồn này trong đơn vị bits.
„ Giải
„ Lượng tin riêng của mỗi tin là
1/161/161/161/161/81/81/41/4
p(u7)p(u6)p(u5)p(u4)p(u3)p(u2)p(u1)p(u0)
44443322
I(u7)I(u6)I(u5)I(u4)I(u3)I(u2)I(u1)I(u0)
Trang 53
Lý thuyết Thông tin - Khoa Công Nghệ Thông Tin
Ví dụ (tt)
„ Lượng tin trung bình của nguồn là
I(U) = (1/4) × 2 + (1/4) × 2 + (1/8) × 3 + (1/8) × 3 + (1/16) × 4 
+ (1/16) × 4 + (1/16) × 4 + (1/16) × 4 = 2,75 bits.
„ Điều này nói lên một ý nghĩa quan trọng rằng, chúng ta có thể
biểu diễn mỗi tin trong nguồn U bằng một chuỗi có chiều dài 
trung bình là 2,75 bits. Nó sẽ tốt hơn so với trong trường hợp 
chúng ta không chú ý đến cấu trúc thông kê của nguồn. Lúc đó
chúng ta sẽ biểu diễn mỗi tin trong 8 tin của nguồn bằng các 
chuỗi có chiều dài là 3 bits.