Bài giảng Khoa học dịch vụ - Chương 6: Bài toán định vị và phân bố trong dịch vụ - Hà Quang Thụy
Bài toán định vị và phân bố
❖ Thường gặp trong cung cấp dịch vụ
❖ Quyết định mở rộng phạm vi: Thuyết phục về độ hiệu quả
❖ Ràng buộc: trong một tài nguyên hạn chế.
❖ Có bổ sung ngân sách ?
➢Nội dung của chương
❖ Cung cấp ví dụ cho bài toán định vị
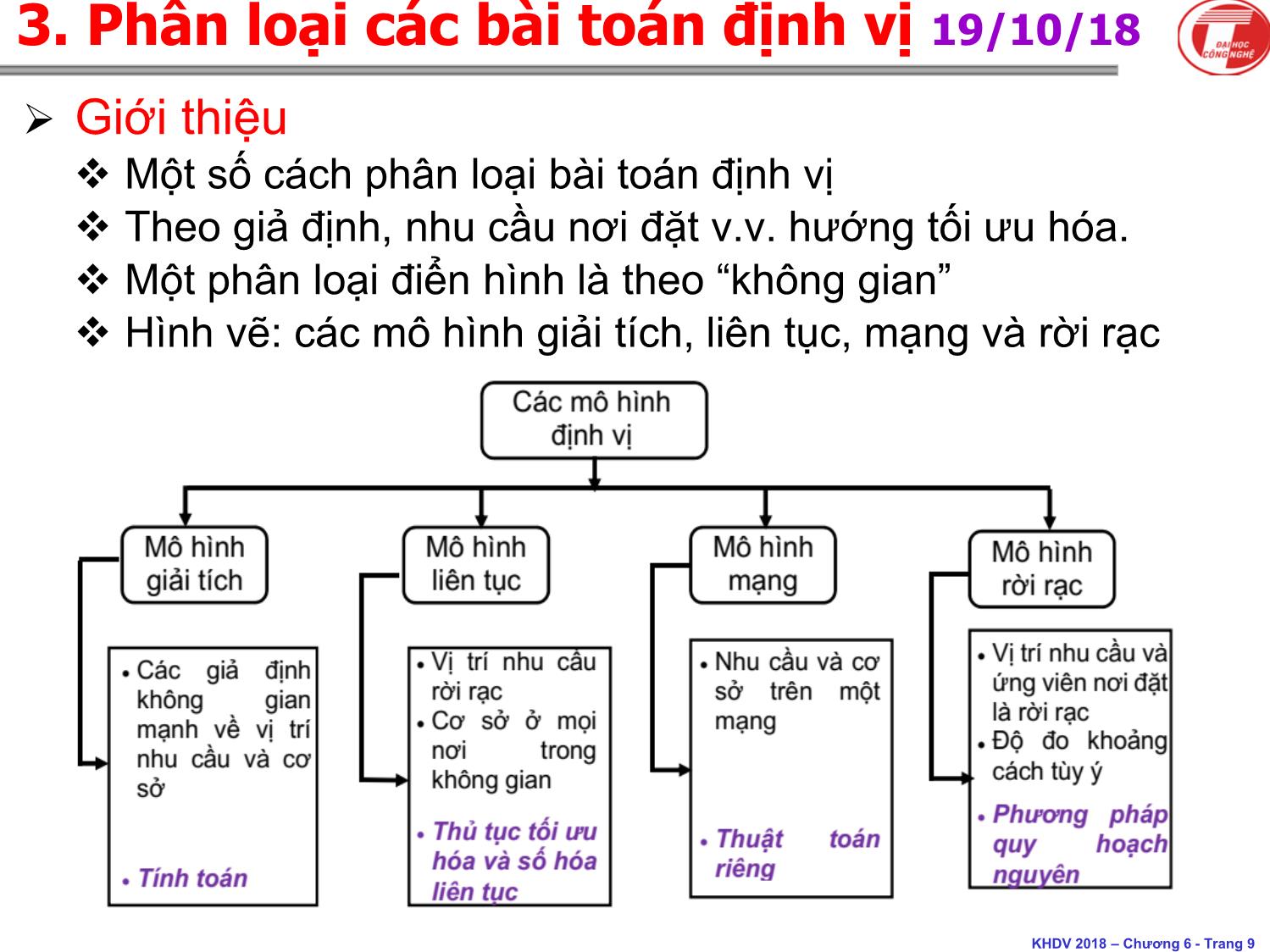
❖ Giới thiệu các loại bài toán định vị
❖ Các mô hình phủ
❖ Các mô hình khoảng cách trung bình theo trọng số
❖ Mô hình đa muc tiêu: kết hợp hai dòng mô hình
❖ Mô hình phân bố
❖ Mô hình nhượng quyền thương mại

Trang 1

Trang 2

Trang 3
Trang 4

Trang 5

Trang 6

Trang 7

Trang 8
Trang 9

Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Khoa học dịch vụ - Chương 6: Bài toán định vị và phân bố trong dịch vụ - Hà Quang Thụy", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Khoa học dịch vụ - Chương 6: Bài toán định vị và phân bố trong dịch vụ - Hà Quang Thụy

NHẬP MÔN KHOA HỌC DỊCH VỤ CHƯƠNG 6. BÀI TOÁN ĐỊNH VỊ VÀ PHÂN BỐ TRONG DỊCH VỤ PGS. TS. HÀ QUANG THỤY HÀ NỘI 09-2018 TRƯỜNG ĐẠI HỌC CÔNG NGHỆ ĐẠI HỌC QUỐC GIA HÀ NỘI 1 KHDV 2018 – Chương 6 - Trang 2 ➢Giới thiệu ➢ Một số ví dụ ➢ Phân loại các bài toán định vị ➢ Vấn đề phủ ➢ Vấn đề định vị: Cực tiểu khoảng cách trung bình trọng số nhu cầu Nội dung chương Mark S. Daskin. Network and Discrete Location Models, Algorithms, and Applications (2nd edition). John Wiley & Sons, 2013 KHDV 2018 – Chương 6 - Trang 3 ➢ Bài toán định vị và phân bố ❖ Thường gặp trong cung cấp dịch vụ ❖ Quyết định mở rộng phạm vi: Thuyết phục về độ hiệu quả ❖ Ràng buộc: trong một tài nguyên hạn chế. ❖ Có bổ sung ngân sách ? ➢Nội dung của chương ❖ Cung cấp ví dụ cho bài toán định vị ❖ Giới thiệu các loại bài toán định vị ❖ Các mô hình phủ ❖ Các mô hình khoảng cách trung bình theo trọng số ❖ Mô hình đa muc tiêu: kết hợp hai dòng mô hình ❖ Mô hình phân bố ❖ Mô hình nhượng quyền thương mại 1. Giới thiệu KHDV 2018 – Chương 6 - Trang 4 ➢Dịch vụ xe cấp cứu tại Austin ❖ Thành phố Austin, bang Texas, Mỹ ❖ Là dịch vụ thứ ba: sau DV cảnh sát và DV cứu hỏa ➢Hiện trạng ❖ Một đội xe cấp cứu thường trực 24 giờ/nghỉ 24 giờ ❖ Cần căn hộ có thể ăn, ngủ, thư giãn ❖ Xe cấp cứu: trang bị y tế đắt tiền, phải đưa lên căn hộ ❖ Thời gian đưa trang bị mất 1-2 phút ➢Yêu cầu ❖ Cần định vị ví trí đặt xe cấp cứu: có ngay xe, an toàn ❖ Một số câu hỏi : ❖ Cần bao nhiêu cơ sở đặt xe cứu thương? ❖ Vị trí cụ thể của các cơ sở đặt xe ? ❖ Loại mức xe hoạt động tại mỗi cơ sở ? Hai loại: Thường/cao cấp. ❖ Mục tiêu: Một mục tiêu đã nói trước đây 2. Ví dụ 1: định vị xe cấp cứu KHDV 2018 – Chương 6 - Trang 5 ➢ Giới thiệu ❖ Yêu cầu của Cơ quan quản lý thảm họa (The Federal Emergency Management Agency: FEMA) ❖ Mỗi quận cần thành lập Trạm phục hồi thảm họa ❖ Diện tích 2000 feet vuông, hệ thống sưởi, điều hòa, điện thoại và fax, không bị ngập lụt, + các tiêu chuẩn khác ❖ FEMA yêu cầu quận Alachua đặt ít nhất 3 trạm ➢Một số mục tiêu ❖ Cực tiểu khoảng cách trung bình cư dân phải đi tới trạm gần nhất ❖ Cực tiểu khoảng cách cực đại mà mọi cư dân phải đi tới trạm gần nhất ❖ Cực tiểu số trung tâm cần thiết đảm bảo mọi cư dân nằm trong khoảng cách cho trước tới trạm gần nhất ❖ Cực đại xác suất có 1 trạm làm việc khi thảm họa xảy ra Ví dụ 2: Định vị trạm phục hồi thảm họa KHDV 2018 – Chương 6 - Trang 6 ➢ Một số nội dung ❖ Quận được chia thành 6600 lô với 3900 lô đáp ứng yêu cầu FEMA ❖ Giao cho nhóm sinh viên: Vượt quá khả năng ➢ Hướng giải quyết sơ bộ ❖ Sử dụng phần mềm thương mại ❖ Tạo thành 198 điểm yêu cầu với 162 định vị ứng viên ❖ Chia hai giai đoạn ❖ Giai đoạn 1: Mô hình toán học tìm ra ba điểm mà hầu như dân cư ở khoảng cách 20 dặm ❖ Giai đoạn 2: Tìm kiếm nghiệm thực sự yêu cầu FEMA Ví dụ: Định vị trạm phục hồi thảm họa KHDV 2018 – Chương 6 - Trang 7 ➢ Giới thiệu ❖ Công ty Shlumberger cung cấp công tơ khí đốt, điện, nước tự động toàn cầu ❖ Bài toán cốt lõi: Định vị bộ thu công tơ (automated meter readers: AMR) ➢Nội dung ❖ Bộ thu thường đặt ở cột điện thoại ❖ Phạm vi bộ thu: một hàm theo chiều cao cột, môi trường ❖ Mỗi bộ thu quản lý nhiều nhất khoảng cách 540 m, tuy nhiên, thực tiễn nhỏ hơn đáng kể ❖ Mục tiêu: Cực tiểu số bộ thu cần để đọc được mọi công tơ trong một vùng lãnh thổ & đảm bảo giới hạn bộ thu ❖ Công ty làm việc với HTTT địa lý. Rất chậm, cần cải tiến ❖ Phát triển 116.000 địa điểm khách hàng và hơn 20.000 cột điện thoại Hệ thống Công tơ mét tự động KHDV 2018 – Chương 6 - Trang 8 ➢ Giới thiệu ❖ Ung thư tiền liệt tuyến 225.000 ở Mỹ và nửa triệu thế giới ❖ Brachytherapy thủ tục điều trị phổ biến mà đặt khoảng 60-150 hạt phóng xạ nhỏ ở tuyến liệt để tấn công khối u ❖ Bài toàn: bao nhiêumồi và nơi đặt chúng ? ❖ Phương pháp truyền thống xác định mồi: đòi hỏi siêu âm hoặc cắt lớp. Bác sỹ xác định vị trí đặt hạt. Nhiều điểm hạn chế. ➢Phương pháp cải tiến ❖ Mục tiêu: 95% các điểm ảnh ba chiều (voxel) nhận được lượng phóng xạ cần thiết ❖ Định vị các mồi để tối đa hóa các điểm đáp ứng yêu cầu quy định hoặc tối thiểu hóa sai lệch so với yêu cầu ❖ PP mới cải thiện định vị hạt giống, làm giảm đáng kể thời gian lập kế hoạch phẫu thuật. Ví dụ 4: Định vị mồi cho Brachytherapy KHDV 2018 – Chương 6 - Trang 9 ➢ Giới thiệu ❖ Một số cách phân loại bài toán định vị ❖ Theo giả định, nhu cầu nơi đặt v.v. hướng tối ưu hóa. ❖ Một phân loại điển hình là theo “không gian” ❖ Hình vẽ: các mô hình giải tích, liên tục, mạng và rời rạc 3. Phân loại các bài toán định vị 19/10/18 KHDV 2018 – Chương 6 - Trang 10 ➢ Giới thiệu ❖ Là mô hình đơn giản nhất: “phương pháp giải tích” ! ❖ Giả định mạnh: về bản chất nhu cầu và vị trí đặt ❖ Ví dụ: Nhu cầu là đồng nhất lan trong toàn khu vực DV ❖ Tính đồng nhất có hạn chế trong thực tiễn ➢Giải pháp ❖ Mô hình định vị phân tích dễ giải ❖ Giả sử khu vực cần dịch là hình vuông diện tích a ❖ Mỗi cơ sở (cung cấp) dịch vụ: một hình thoi (vuông) cung cấp dịch vụ tại cơ sở đó ❖ Nếu có N cơ sở thì diện tích mỗi vùng là a/N và khoảng cách trung bình giữa một điểm yêu cầu tới tâm của vùng là * Mô hình định vị giải tích KHDV 2018 – Chương 6 - Trang 11 * Mô hình định vị giải tích KHDV 2018 – Chương 6 - Trang 12 ➢Giải pháp ❖ Giá mỗi cơ sở là f đơn vị tiền tệ ❖ Chi phí cung cấp dịch vụ đáp ứng nhu cầu mỗi dặm: c, ❖ Mật độ nhu cầu là p theo từng dặm vuông, ❖ Tổng chi phí là một hàm theo N ❖ Số lượng các cơ sở tối ưu được tính từ hàm mục tiêu (4.1) ❖ Nếu đưa đạo hàm của (4.1) tới 0 thì số lượng tối ưu các phương tiện là (4.2) ❖ Thế (4.2) vào (4.1) ta có (4.3) Xác định số lượng cơ sở phục vụ KHDV 2018 – Chương 6 - Trang 13 ➢ Nhận xét ❖ Phương trình (4.2): Số lượng tối ưu các phương tiện phục vụ tăng tuyến tính theo diện tích khu vực phục vụ; Số lượng tối ưu giảm theo chi phí đơn vị cơ sở ❖ Phương trình (4.3): Tổng chi phí tối ưu tăng tuyến tính theo diện tích khu vực phục vụ; Tổng chi phí tăng theo mật độ nhu cầu dịch vụ ❖ Hình 4.3 Biểu diễn đồ thị KHDV 2018 – Chương 6 - Trang 14 ➢ Giới thiệu ❖ Phân bố dịch vụ cho các bang nước Mỹ: Mỗi trạm 1 triệu USD, giá nhu cẫu mỗi dặm là 0.1 USD ❖ Phương án phân bố đồng nhất nhu cầu không phù hợp ❖ Trung bình 89 người/dặm vuông: 5 người ở Wyoming, trung bình 160 người, cao 965 người ở New Jersey. ❖ Bảng dưới cho thấy tác động của giả định này Mô hình định vị giải tích: Ví dụ KHDV 2018 – Chương 6 - Trang 15 ➢ Dòng đầu ❖ Dòng đầu: Toàn nước Mỹ như một khu vực DV duy nhất ❖ 3,11 triệu dặm vuông với 280 triệu người ❖ Mô hình toàn bộ: 514 cơ sở với chi phí 1,541 tỷ USD ❖ Phân bổ trạm không phù hợp tới các khu vực domật độ không đồng đều. Quá nhiều trạm, tổng chi phí quá dự toán ➢Các dòng khác ❖ Chia khu vực phục vụ ba vùng: thấp, trung bình, cao. Phù hợp hơn song vẫn thô. ❖ Mô hình định vị giải tích chưa chính xác song cho hiểu biết quan trọng về định vị. Mô hình định vị giải tích: Ví dụ KHDV 2018 – Chương 6 - Trang 16 ➢ Giới thiệu ❖ Tên “liên tục” song giả thiết nhu cầu được đặt “rời rạc”, ❖ Mô hình làm nhẹ đi giả thiết mạnh của mô hình giải tích ❖ Nhu cầu thường tập trung tại một số điểm ❖ Giả thiết phù hợp thực tiễn ➢Phân tích sơ bộ ❖ Các cơ sở đặt bất kỳ nơi nào: hạn chế khả năng ứng dụng thực tiễn ❖ Giải pháp: kỹ thuật tối ưu phi tuyến liên tục. Thủ tục số ❖ Bài toán Weber là điển hình cho mô hình định vị liên tục * Mô hình định vị liên tục KHDV 2018 – Chương 6 - Trang 17 ➢Bài toán ❖ Cho ❖ Cho n điểm nhu cầu: 1, 2, , j, , n ❖ Điểm j định vị tại (xj, yj), Nhu cầu tại điểm j là hj; ❖ Yêu cầu ❖ Tìm vị trí (Xo, Yo) tối thiểu tổng khoảng cách với trọng số nhu cầu giữa cơ sở và các điểm nhu cầu (4.5) ➢Phân tích ❖ Trực quan: miếng gỗ dán, tại mỗi điểm nhu cầu: khoan một lỗ và đặt một ròng rọc ma sát; đưa một sợi chỉ xuyên mỗi lỗ với một trọng lượng tỷ lệ với nhu cầu ❖ Mọi sợi chỉ gắn trên ròng rọc tương ứng và gắn vào một vòng duy nhất ❖ Vị trí vòng cân bằng là định vị Weber Bài toán Weber KHDV 2018 – Chương 6 - Trang 18 ➢Thủ tục ❖ Giải bằng thủ tục lặp Weiszfeld ❖ Thủ tục tính toán một dãy lời giải ❖ Thủ tục lặp là giá trị (Xo, Yo) tại bước k: (4.6) (4.7) ❖ Trong đó là số dương rất nhỏ, tham số đầu vào. ➢Phân tích ❖ Sử dụng để tránh chia cho 0, ❖ Hội tụ nhanh với hầu hết trường hợp Giải bài toán Weber KHDV 2018 – Chương 6 - Trang 19 ➢Giới thiệu ❖ Yêu cầu tìm vị trí cơ sở cực tiểu hóa khoảng cách theo trọng số yêu cầu từ cơ sở tới 67 quận của bang Pennsylvania. ❖ Nhu cầu ở các điểm thoi, độ lớn nhu cầuđộ lớn thoi ❖ P/án xuất phát (80.5,42), hội tụ nhanh về (76,403, 40,355) ❖ Nhạy cảm với phương án xuất phát Giải bài toán Weber: ví dụ lời giải KHDV 2018 – Chương 6 - Trang 20 ➢Trả lời các câu hỏi ❖ Có bao nhiêu cơ sở cần phải đặt? ❖ Nơi nào từng cơ sở được đặt? ❖ Mỗi cơ sở nên có kích thước, quy mô ra sao? ❖ Nhu cầu dịch vụ mà mỗi cơ sở cần đáp ứng ra sao? * Mô hình định vị mạng và rời rạc Mark S. Daskin. Network and Discrete Location: Models, Algorithms, and Applications. John Wiley & Sons, 2013 KHDV 2018 – Chương 6 - Trang 21 ➢ Giới thiệu ❖ Giả thiết: Tồn tại mạng nền cho bài toán ❖ Ví dụ: đường cao tốc, đường trục, đường cục bộ trong thành phố; Mạng hệ thống quốc lộ; Mạng cung cấp nước ❖ Định vị mạng thường yêu cầu tìm lời giải đa thức theo kích thước bài toán ❖ Phổ biến định vị mạng theo cấu trúc đặc biệt: Cây ❖ Sơ đồ 10 t/phố lớn nhất Mỹ: nhu cầu/dân số nút (mầu xanh) và khoảng cách. * Mô hình định vị mạng 732 103 278 159 163 101 96 94 340 111 KHDV 2018 – Chương 6 - Trang 22 ➢ Trọng số nhu cầu ❖ Tổng nhu cầu = 2188. Ma trận đường đi ngắn nhất ❖ Bài toán: Tìm một thành phố trên cây để tổng khoảng cách với trọng số nhu cầu nhỏ nhất → tích vô hướng vector trên bảng với vector trọng số. ❖ NY: 159*1373+103*468+278*706+101*1505+163*1729+94*1757+ 98*2604+349*2970+111*2901. Tổng 2.675.502 Mô hình định vị mạng 732 159 103 278 101 163 94 98 349 111 KHDV 2018 – Chương 6 - Trang 23 ❖ Thuật toán Goldman (1971): 1. X nút lá bất kỳ trên cây 2. Nếu nhu cầu (X) nửa tổng nhu cầu thì X là nút cần chọn, 3. ngược lại, gọi Y là nút kết nối X: nhu cầu (Y) nhu cầu (Y)+ nhu cầu (X). Loại bỏ X và cung (X,Y) Tính ví dụ: Chọn Chicago. Tính đúng đắn ? Mô hình định vị mạng KHDV 2018 – Chương 6 - Trang 24 Mô hình định vị mạng KHDV 2018 – Chương 6 - Trang 25 ➢ Giới thiệu ❖ Nhu cầu rời rạc, định vị rời rạc → vùng dịch vụ được chia thành các tiểu vùng. Ví dụ, xe cứu thương: 358 tiểu vùng ❖ Tiểu vùng → điểm, có “lỗi” nhỏ, các cư dân ở tiểu vùng có khác biệt khoảng cách ❖ Nhu cầu tiểu vùng gắn với tiểu vùng. Ví dụ xe cứu thương: Số cuộc gọi quá khứ, số người già v.v. ❖ Phục vụ có thể tọa lạc tại các tiểu vùng. ❖ Khoảng cách (tiểu vùng, tọa lạc) do người dùng chọn. ❖ Tồn tại nhiều độ đo khoảng cách trong nhiều bài toán ❖ Trong định vị địa lý: khoảng cách chu trình lớn, khoảng cách cao tốc, thời gian di chuyển, giá thành v.v. * Mô hình định vị rời rạc KHDV 2018 – Chương 6 - Trang 26 ➢ Các loại định vị rời rạc ❖ Phụ thuộc dạng hàm mục tiêu Định vị rời rạc: Phân loại KHDV 2018 – Chương 6 - Trang 27 ➢ Cuốn sách The Numerati của StephenBaker: ❖ Stephen Baker. The Numerati. Houghton Mifflin Harcourt, 2008 ❖ Ứng dụng toán học nhằm xác định đặc điểm người lao động, người tiêu dùng, cử tri ❖ Cá nhân gắn các đặc trưng: tuổi, giới tính, vị trí nhà, đi làm hay không, thu nhập, sở hữu/thuê nhà, số lượng xe ô-tô, khi đi du lịch nước ngoài. ❖ “Khoảng cách”: độ khác biệt các đặc trưng nói trên. ❖ Tìm 10 cá nhân “đại diện” cho toàn tiểu vùng. ❖ Bài toán định vị Định vị rời rạc: khoảng cách KHDV 2018 – Chương 6 - Trang 28 ➢ Giới thiệu ❖ Mô hình phủ: Covering model (CM) ❖ Mô hình phủ tập (Set CM): dạng cơ bản của mô hình phủ ❖ Phát biểu đơn giản song rất khó giải ❖ Yêu cầu mọi nút yêu cầu cần được đáp ứng ❖ Hai mô hình đơn giản cố định số lượng nhà cung cấp p là một giá trị đầu vào người dùng ❖ Mô hình phủ cực đại (maximal covering model): cực đại số yêu cầu được phủ. ❖ Mô hình trung tâm p (p-center model): cực tiểu khoảng cách phủ/thời gian yêu cầu phủ mọi yêu cầu ❖ Ngầm định: Phủ theo khoảng cách. Chuyển dạng sang thời gian, giá thành, v.v. 4. Mô hình phủ tập KHDV 2018 – Chương 6 - Trang 29 ➢ Phủ tập tối thiểu phương tiện ❖ Yêu cầu: mọi yêu cầu cần được đáp ứng ❖ Cho tập các nút yêu cầu I ❖ Cho tập các định vị phương tiện ứng viên J, với giá thành fj tại định vị j. ❖ Cho khoảng cách dij từ nút yêu cầu i tới định vị ứng viên j. ❖ Cho một giới hạn khoảng cách Dc mà chỉ định vị tới yêu cầu nếu khoảng cách Dc ❖ Phát biểu bài toán dạng quy hoạch nguyên Tối thiểu phương tiện KHDV 2018 – Chương 6 - Trang 30 Dạng đồ thị ➢ Ví dụ ❖ Khoảng cách ❖ Nhu cầu theo đơn vị thời gian mỗi nút KHDV 2018 – Chương 6 - Trang 31 Dạng đồ thị ➢ Ví dụ ❖ Khoảng cách giới hạn 8
File đính kèm:
 bai_giang_khoa_hoc_dich_vu_chuong_6_bai_toan_dinh_vi_va_phan.pdf
bai_giang_khoa_hoc_dich_vu_chuong_6_bai_toan_dinh_vi_va_phan.pdf

