Bài giảng Giải tích II - Chương 5: Tích phân đường - Nguyễn Văn Quang
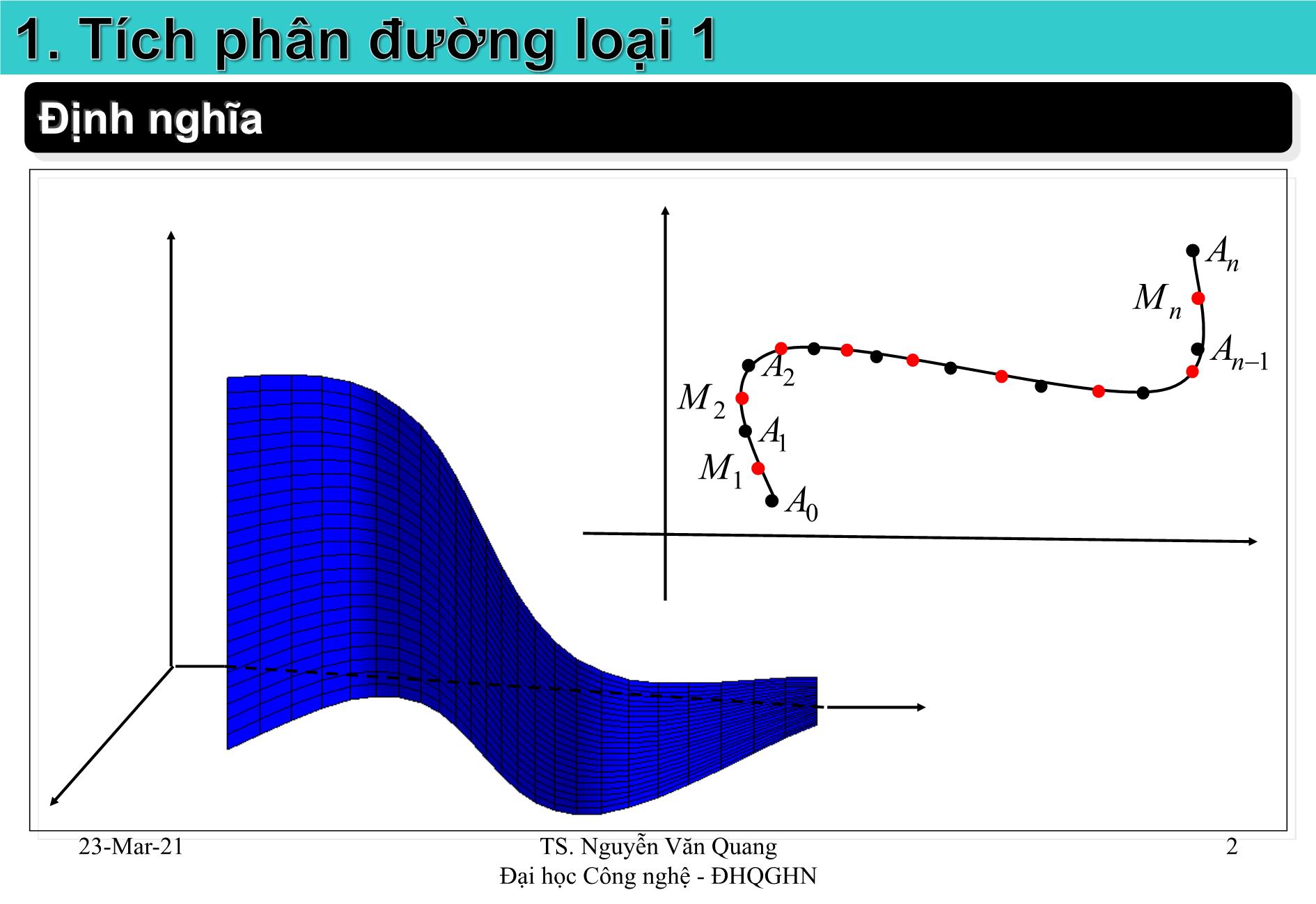
Xét hàm f f x y ( , ) xác định trên đường cong C.
Chia C một cách tùy ý ra n đường cong nhỏ bởi các điểm A A A 0 1 , ,., . n
Độ dài tương ứng L L L 1 2 , ,., . n
Trên mỗi cung A A i i 1lấy tuỳ ý một điểm M x y i i i ( , ).
Lập tổng Riemann:
lim n, không phụ thuộc cách chia C, và cách lấy điểm Mi
được gọi là tích phân đường loại một của f = f(x,y) trên cung C.

Trang 1
Trang 2

Trang 3

Trang 4

Trang 5

Trang 6

Trang 7

Trang 8

Trang 9

Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Giải tích II - Chương 5: Tích phân đường - Nguyễn Văn Quang", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Giải tích II - Chương 5: Tích phân đường - Nguyễn Văn Quang

điểm A đến điểm B dưới tác dụng của lực: 퐹 = 푃 . 푖 + 푄 . 푗 , ∈ . Hãy tính công W của lực đó sinh ra. 23-Mar-21 TS. Nguyễn Văn Quang 22 Đại học Công nghệ - ĐHQGHN Bài toán Chia cung một cách tùy ý ra n đường cung nhỏ bởi các điểm chia: A0( x 0 , y 0 ), A 1 ( x 1 , y 1 ),..., An ( x n , y n ). Khi đó: Ai 1 A i x i i y i j Lấy M i (,). x i y i A i 1 A i Cung AA ii 1 nhỏ, nên có thể coi nó xấp xỉ dây cung AAii 1 và FM () i không đổi (về chiều và độ lớn) trên cung đó. Do đó, công của lực sinh ra khi chất điểm di chuyển từ 푖−1 đến 푖 theo cung AA ii 1 sẽ xấp xỉ là: F()()() Mi A i 1 A i P M i x i Q M i y i 23-Mar-21 TS. Nguyễn Văn Quang 23 Đại học Công nghệ - ĐHQGHN Bài toán Vậy công W của lực sinh ra sẽ xấp xỉ với: n W P(,)(,) xi y i x i Q x i y i y i i 1 Do đó, giới hạn của tổng trên khi 푛 → ∞ chính là công của lực: n W= limP ( xi , y i ) x i Q ( x i , y i ) y i n i 1 23-Mar-21 TS. Nguyễn Văn Quang 24 Đại học Công nghệ - ĐHQGHN Định nghĩa P P( x , y ), Q Q ( x , y ) xác định trên đường cong C có hướng. Chia C một cách tùy ý ra n đường cong nhỏ bởi các điểm: A0( x 0 , y 0 ), A 1 ( x 1 , y 1 ),..., An ( x n , y n ). Trên mỗi cung AA ii 1 lấy tuỳ ý một điểm M i (,); x i y i A i 1 A i xi i yi j n Lập tổng Riemann: IPMQ n ()() i () xx i i 1 M i (yi yi 1) i 1 II lim n , không phụ thuộc cách chia C, và cách lấy điểm Mi n I P(,)(,) x y dx Q x y dy C được gọi là tích phân đường loại hai của P(x,y) và Q(x,y) trên cung C. 23-Mar-21 TS. Nguyễn Văn Quang 25 Đại học Công nghệ - ĐHQGHN Tính chất 1) Tích phân đường loại hai phụ thuộc chiều lấy tích phân trên C: Pdx Qdy Pdx Qdy AB BA 2) Nếu C được chia làm hai cung C1 và C2 rời nhau: Pdx Qdy Pdx Qdy Pdx Qdy C CC12 23-Mar-21 TS. Nguyễn Văn Quang 26 Đại học Công nghệ - ĐHQGHN Cách tính tích phân đường loại hai: 1) C: x = x(t), y = y(t), t = a ứng với điểm đầu, t = b: điểm cuối cung. P(,)(,)(,)(,) x y dx Q x y dy P x y dx Q x y dy CCC Chia [a,b] thành n đoạn: a t0 t 1 t 2 tn b ñònh lyù Lagrange * xi x i x i 11 x()() t i x t i x () tii t ** Chọn điểm trung gian M i x ( t i ), y ( t i ) , khi đó: n ** P(,) x y dx lim P ((),()) x ti y t i x i C n i 1 n b *** P(,) x y dx lim P x (),() ti y t i x () t i t i P x( t ), y ( t ) x ( t ) dt C n i 1 a b P(,) x y dx Q (,) x y dy P x (),() t y t x () t Q x (),() t y t y () t dt Ca 23-Mar-21 TS. Nguyễn Văn Quang 27 Đại học Công nghệ - ĐHQGHN Cách tính Các hàm 푃( , ) và 푄( , ) liên tục trên tập mở D chứa cung trơn C. 2) C: y = y(x), x = x1 là hoành độ điểm đầu, x = x2: điểm cuối cung. x2 P(,) x y dx Q (,) x y dy P (,()) x y x Q (,()) x y x y () x dx Cx1 3) C: x = x(y), y = y1 là tung độ điểm đầu, y = y2: điểm cuối cung. y2 P(,) x y dx Q (,) x y dy P ((),) x y y x () y Q ((),) x y y dy Cy1 23-Mar-21 TS. Nguyễn Văn Quang 28 Đại học Công nghệ - ĐHQGHN Tích phân đường loại 2 trong không gian Các hàm P(x,y,z), Q(x,y,z) và R(x,y,z) liên tục trên tập mở D chứa cung trơn AB. n Pdx Qdy Rdz lim P ( Mi ) x i Q ( M i ) y i R ( M i ) z i AB n i 1 Cung AB có phương trình tham số: xxtyytzzt ( ), ( ), ( ); atb Pdx Qdy Rdz AB b P((),(),()) x t y t z t x () t dt Q ((),(),()) x t y t z t y () t dt R ((),(),()) x t y t z t z () t dt a b P x ()()() t Q y t R z t dt a 23-Mar-21 TS. Nguyễn Văn Quang 29 Đại học Công nghệ - ĐHQGHN Tích phân đường loại 2 trong không gian Giả sử: 퐅( , , ) = 푃 , , 퐢 + 푄 , , 퐣 + 푅 , , 퐤 là một trường vector xác định trên cung AB. Nếu cung AB được cho bởi phương trình vector: r()()()()t x t i y t j z t k Tích phân đường của F trên cung AB là (công của lực F sinh ra khi di chuyển một vật trên đường cong AB): Fd r F( r ( t )) r '( t ) dt AB AB 23-Mar-21 TS. Nguyễn Văn Quang 30 Đại học Công nghệ - ĐHQGHN Ví dụ 2 Tính I ( x 3 y ) dx 2 ydy , trong đó C là biên tam giác OAB C với O(0,0); A(1,1); B(0,2), ngược chiều kim đồng hồ. I C OA AB BO Phương trình OA: y = x B Hoành độ điểm đầu: x = 0 Hoành độ điểm cuối: x = 1 A 1 2 I1 ( x 3 x ) dx 2 xdx OA 0 O 1 2 17 I1 ( x 5 x ) dx OA 0 6 23-Mar-21 TS. Nguyễn Văn Quang 31 Đại học Công nghệ - ĐHQGHN Phương trình AB: y = 2 – x B Hoành độ điểm đầu: x = 1 A Hoành độ điểm cuối: x = 0 0 11 2 O I2 ( x 3(2 x )) dx 2( 2 x ) ( 1) dx AB 1 6 Phương trình BO: x = 0 Tung độ điểm đầu: y = 2 0 2 4 Tung độ điểm cuối: y = 0 I3 (0 3 y ) 0 dy 2 y dy BO 2 17 11 IIII 1 2 3 43 66 23-Mar-21 TS. Nguyễn Văn Quang 32 Đại học Công nghệ - ĐHQGHN 22 Tính I ydx xdy , trong đó C là cung x y 2, x từ O(0,0) C đến A(1,1), chiều kim đồng hồ. x rcos t Sử dụng tọa độ cực y rsin t x22 y 2 x r 2cos t Phương trình tham số cung C: x 2cos t cos t 1 cos2 t y 2cos t sin t sin 2 t tt ; 1224 /4 I sin 2 t ( 2sin 2 t ) (1 cos2 t ) (2cos2 t ) dt 1 /2 23-Mar-21 TS. Nguyễn Văn Quang 33 Đại học Công nghệ - ĐHQGHN Tính I ydx zdy xdz với C là đường cong có phương trình tham số: C x a cos t , y a sin t , z bt ,0 t 2 theo hướng tăng dần của biến t. 2 I asin t ( a sin tdt ) bt ( a cos tdt ) a cos t ( bdt ) 0 2 22 2 I asin t abt cos t ab cos t dt a 0 23-Mar-21 TS. Nguyễn Văn Quang 34 Đại học Công nghệ - ĐHQGHN 2 2 2 I ()()() y z dx z x dy x y dz với C là giao của mặt: x y z 4, C yx tan ;0 , ngược chiều kim đồng hồ nhìn theo hướng trục Ox. Từ phương trình của đường cong C, ta có: x2 x 2tan 2 z 2 4 xz22 1 4cos2 4 Tham số đường cong C qua hệ tọa độ trụ: x 2cos cos t ; y 2sin cos t ; z 2sin t (0 t 2 ) 2 I (2sin cos t 2sin t )( 2cos sin t ) (2sin t 2cos cos t )(-2sin sin t ) dt 0 2 (2cos cost 2sin cos t ) (2cos t ) dt 8 2 sin 0 4 23-Mar-21 TS. Nguyễn Văn Quang 35 Đại học Công nghệ - ĐHQGHN Công thức Green C là biên của miền D. Chiều dương qui ước trên C là chiều mà đi theo chiều này ta thấy miền D ở phía bên tay trái. Miền D được gọi là miền đơn liên nếu nó bị giới hạn bởi một đường cong kín. Ngược lại D được gọi là miền đa liên nếu nó bị giới hạn bởi nhiều đường cong kín. Trong đa số trường hợp, chiều dương qui ước là ngược chiều kim đồng hồ. Trong trường hợp tổng quát điều này không đúng. 23-Mar-21 TS. Nguyễn Văn Quang 36 Đại học Công nghệ - ĐHQGHN Công thức Green Miền đơn liên Miền đa liên 23-Mar-21 TS. Nguyễn Văn Quang 37 Đại học Công nghệ - ĐHQGHN Công thức Green D là miền (đơn liên hoặc đa liên) đóng, giới nội trong mặt phẳng với biên C (kín) liên tục, trơn từng khúc. 푃( , ), 푄( , ) và các đạo hàm riêng cấp 1 liên tục trên miền D. QP P(,)(,) x y dx Q x y dy dxdy CD xy Dấu + nếu chiều lấy tích phân trùng chiều dương qui ước (đi theo chiều lấy tích phân, miền D nằm ở bên tay trái) Điều kiện để sử dụng công thức Green: 1) C là cung kín. 2) P(x,y), Q(x,y) và các đạo hàm riêng cấp 1 liên tục trên miền D có biên C. 23-Mar-21 TS. Nguyễn Văn Quang 38 Đại học Công nghệ - ĐHQGHN 2 Tính I ( x 3 y ) dx 2 ydy , trong đó C là biên tam giác OAB C với O(0,0); A(1,1); B(0,2), ngược chiều kim đồng hồ. Cung C kín. B P( x , y ) x2 3 y ; Q ( x , y ) 2 y A P(x,y), Q(x,y) và các đạo hàm riêng cấp 1 liên tục trên miền D có biên C. O 2 QP I ( x 3 y ) dx 2 ydy dxdy CD xy 12 x 03 dxdy dx( 3) dy 3 D 0 x 23-Mar-21 TS. Nguyễn Văn Quang 39 Đại học Công nghệ - ĐHQGHN 22 Tính I ()() x y dx x y dy , trong đó C nửa trên đường tròn: C x 22 y 2 x cùng chiều kim đồng hồ. Cung C không kín. III 12 C C AO AO QP I1 dxdy C AO D xy /2 2cos 2(x y ) 2( x y ) dxdy d 4 r cos r dr 2 D 00 0 228 8 I2 ( x 0) dx ( x 0) 0 dx III 12 2 2 3 3 Có thể giải bằng cách viết phương trình tham số cung C. 23-Mar-21 TS. Nguyễn Văn Quang 40 Đại học Công nghệ - ĐHQGHN ()()x y dx x y dy Tính I 22 , trong đó C đường tròn: C xy xy 22 4 ngược chiều kim đồng hồ. Cách 1: Cung C kín, nhưng P, Q và các ĐHR cấp 1 không liên tục trên D, không sử dụng công thức Green được !!! Viết phương trình tham số cung C: xt 2cos tt12 0; 2 yt 2sin 2 (2cost 2sin t ) ( 2sin t ) dt (2cos t 2sin t ) 2cos tdt I 2 0 4 23-Mar-21 TS. Nguyễn Văn Quang 41 Đại học Công nghệ - ĐHQGHN Cách 2: Tích phân trên đường tròn: 2 + 2 = 4, nên thay vào mẫu số ta có: ()()x y dx x y dy I C 4 Có thể sử dụng công thức Green trong trường hợp này. 1 I ()() x y dx x y dy 4 C 1 2 ( 1 1)dxdy SD 2 4 xy22 4 4 23-Mar-21 TS. Nguyễn Văn Quang 42 Đại học Công nghệ - ĐHQGHN Ví dụ Tính I (4 y ) dx xdy , trong đó C là cung Cicloid: C x 2( t sin t ), y 2(1 cos t ),0 t 2 (cùng chiều kim đồng hồ). Cung C không kín. 2 I 4 2(1 cos t ) 2(1 cos t ) dt 2( t sin t )(2sin t ) dt 0 2 I 4 t sin tdt 8 0 23-Mar-21 TS. Nguyễn Văn Quang 43 Đại học Công nghệ - ĐHQGHN Ví dụ xy22 Tính I e cos2 xydx sin 2 xydy , trong đó C là đường tròn: C xy22 4, ngược chiều kim đồng hồ. 22 22 P( x , y ) e xy cos(2 xy ) ; Q( x , y ) e xy sin(2 xy ) P 22 2e xy y cos(2 xy ) x sin(2 xy ) y Q 22 2e xy y cos(2 xy ) x sin(2 xy ) x QP I dxdy 0 xy22 4 xy 23-Mar-21 TS. Nguyễn Văn Quang 44 Đại học Công nghệ - ĐHQGHN ydx xdy Tính I 22 , trong đó C là đường cong kín tùy ý, C xy không đi qua gốc O, ngược chiều kim đồng hồ. Trường hợp 1: C không bao quanh gốc O. Sử dụng công thức Green. y P(,) x y xy22 Py122 2 2 2 y xy xy22 x Q(,) x y xy22 Qx122 2 2 2 QP x xy xy22 I dxdy 0 D xy 23-Mar-21 TS. Nguyễn Văn Quang 45 Đại học Công nghệ - ĐHQGHN Trường hợp 2: C bao quanh gốc 0. Không sử dụng công thức Green được vì P, Q và các ĐHR cấp 1 không liên tục trên miền D, có biên là C. Kẻ thêm đường tròn C1 có bán kính a đủ nhỏ để C1 nằm lọt trong C, chọn chiều kim đồng hồ. Green QP III 12 I1 = dxdy 0 CCCC 11 CCD 1 xy 2 2 2 Tính tích phân I2 trên cung tròn: + = Phương trình tham số của cung C1: x acos t , y a sin t , t12 2 , t 0 0 acos t a cos t dt a sin t a sin t dt I2 2 2 III 12 2 2 a 23-Mar-21 TS. Nguyễn Văn Quang 46 Đại học Công nghệ - ĐHQGHN Tích phân không phụ thuộc đường lấy tích phân Định lý: (không phát biểu cho miền đa liên) Giả sử tồn tại miền mở đơn liên D chứa cung AB, sao cho P(x,y), Q(x,y) và các ĐHR cấp 1 của chúng liên tục trong D. Các mệnh đề sau tương đương: QP 1. ,(,) x y D xy 2. Tích phân I Pdx Qdy không phụ thuộc đường cong (trơn từng khúc) AB nối điểm A, B nằm trong D. 3. Tồn tại hàm U(x,y) trên D là vi phân toàn phần của Pdx + Qdy, tức là: dU(,) x y Pdx Qdy 4. Tích phân trên mọi đường cong kín C, trơn từng khúc trong D bằng 0: I Pdx Qdy 0 C 23-Mar-21 TS. Nguyễn Văn Quang 47 Đại học Công nghệ - ĐHQGHN Tích phân không phụ thuộc đường lấy tích phân QP Tích phân không phụ thuộc đường đi xy III 12 B AB AC CB I1 Pxydx(,)(,) Qxydy xx B AC yy, xB AB P( x , yAA ) dx Q ( x , y ) 0 dx x yy A A A C xxAB, I2 Pxydx(,)(,) Qxydy CB yB P( x , y ) 0 dy Q ( x , y ) dy AB xyBB yA I P(,)(,) x yAB dx Q x y dy xyAA 23-Mar-21 TS. Nguyễn Văn Quang 48 Đại học Công nghệ - ĐHQGHN (2,3) Tính I ydx xdy ( 1,2) QP 1 suy ra, tích phân không phụ thuộc đường đi. xy B(2,3) Cách 1: A( 1,2) C 23 I 22dx dy 8 AC CB 12 Cách 2: Tồn tại hàm U(x,y) là vi phân toàn phần của Pdx + Qdy Ux P(,) x y tìm được hàm U(,) x y xy C U Q(,) x y y (2,3) I ydx xdy U(,) x y (2,3) UU(2,3) ( 1,2) 8 ( 1,2) ( 1,2) 23-Mar-21 TS. Nguyễn Văn Quang 49 Đại học Công nghệ - ĐHQGHN (6,8) xdx ydy Tính I , với đường cong không bao quanh gốc tọa độ. (1,0) xy22 QP suy ra, tích phân không phụ thuộc đường đi. xy Tồn tại hàm U(x,y) là vi phân toàn phần của Pdx + Qdy x (1) U (,) x y P (,) x y dx g () y Ux P(,) x y (1) 22 xy 22 U(,)() x y x y g y y Uy Q(,) x y (2) (2) gy ( ) 0 g() y C 22 xy U(,) x y x22 y C I U(,) x y (6,8) UU(6,8) (1,0) 9 (1,0) 23-Mar-21 TS. Nguyễn Văn Quang 50 Đại học Công nghệ - ĐHQGHN xdx ydy Tính I 22 theo đường cong AB tùy ý từ A(1,0) đến B(2,0): AB xy a) Không bao quanh gốc tọa độ. b) Bao quanh gốc tọa độ. QP a) , tích phân I không phụ thuộc đường đi từ A đến B. xy 2 dx 2 Nên ta tính tích phân theo trục hoành: Ix ln ln 2 1 1 x QP b) , tích phân I không phụ thuộc đường đi từ A đến B. xy Tuy nhiên I không thể tính như câu a (theo đường thẳng từ A đến B theo trục hoành), vì không tồn tại miền đơn liên D nào chứa đường thẳng AB và đường cong kín bao quanh gốc O để cho P, Q và các ĐHR cấp 1 liên tục trên D. 23-Mar-21 TS. Nguyễn Văn Quang 51 Đại học Công nghệ - ĐHQGHN Cách 1: Tính theo các đoạn thẳng: AC, CD, DE, EF, FB. trong đó: A(1,0), C(1,1), D(-1,1), E(-1,-1), F(2,-1), B(2,0). Cách 2: Tìm hàm U(x,y) là vi phân toàn phần của P(x,y)dx+Q(x,y)dy x U P(,) x y (1) (1) U (,) x y P (,) x y dx g () y x 22 xy 22 y ln(xy ) U(,)() x y g y Uy Q(,) x y 22 (2) 2 xy (2) gy ( ) 0 g() y C ln(xy22 ) U(,) x y C 2 (2,0) ln 4 ln1 I U(,) x y UU(2,0) (1,0) ln 2 (1,0) 2 Cách 3: Bổ sung thêm đoạn thẳng từ B đến A, đưa vào đường tròn (đủ nhỏ) bao quanh gốc O. Sử dụng công thức Green đối với miền đa liên này. 23-Mar-21 TS. Nguyễn Văn Quang 52 Đại học Công nghệ - ĐHQGHN xy x xy x I (2 ye e cos y ) dx (2 xe e sin y ) dy C a) Tìm hằng số để tích phân I không phụ thuộc đường đi. b) Với ở câu a), tính I biết C là cung tùy ý nối A (0, ) và B (1,0). a) Điều kiện cần để tích phân không phụ thuộc đường đi: QP xy 2exy 2 xye xy e x sin y 2 e xy 2 xye xy e x sin y 1 Đây cũng là điều kiện đủ vì với mọi cung C luôn tìm được miền đơn liên D chứa cung C sao cho P, Q và các ĐHR cấp 1 liên tục trên miền D. 23-Mar-21 TS. Nguyễn Văn Quang 53 Đại học Công nghệ - ĐHQGHN b) Với 1 ta có tích phân: (1,0) xy x xy x I (2 ye e cos y ) dx (2 xe e sin y ) dy (0, ) A(0, ) x 0 Chú ý: tích phân I không phụ thuộc đường đi. yy12 ,0 O B(1,0) I AO OB 01 y 0 I sin ydy ex dx xx 1, 0 0 12 Ie 1 23-Mar-21 TS. Nguyễn Văn Quang 54 Đại học Công nghệ - ĐHQGHN Tích phân không phụ thuộc đường lấy tích phân a) Cho P ( x , y ) y , Q ( x , y ) 2 x ye y . Tìm hàm h(y) thỏa h(1) = 1 sao cho tích phân I h ()(,)()(,) y P x y dx h y Q x y dy không phụ thuộc đường đi. C b) Với h(y) ở câu a), tính I biết C là phần đường cong có phương trình: 4 xy 22 9 36 , ngược kim đồng hồ từ A(3,0) đến B(0,2). a) Điều kiện cần để tích phân không phụ thuộc đường đi: QP xy 23-Mar-21 TS. Nguyễn Văn Quang 55 Đại học Công nghệ - ĐHQGHN
File đính kèm:
 bai_giang_giai_tich_ii_chuong_5_tich_phan_duong_nguyen_van_q.pdf
bai_giang_giai_tich_ii_chuong_5_tich_phan_duong_nguyen_van_q.pdf

