Bài giảng Giải tích II - Chương 4: Tích phân bội ba - Nguyễn Văn Quang

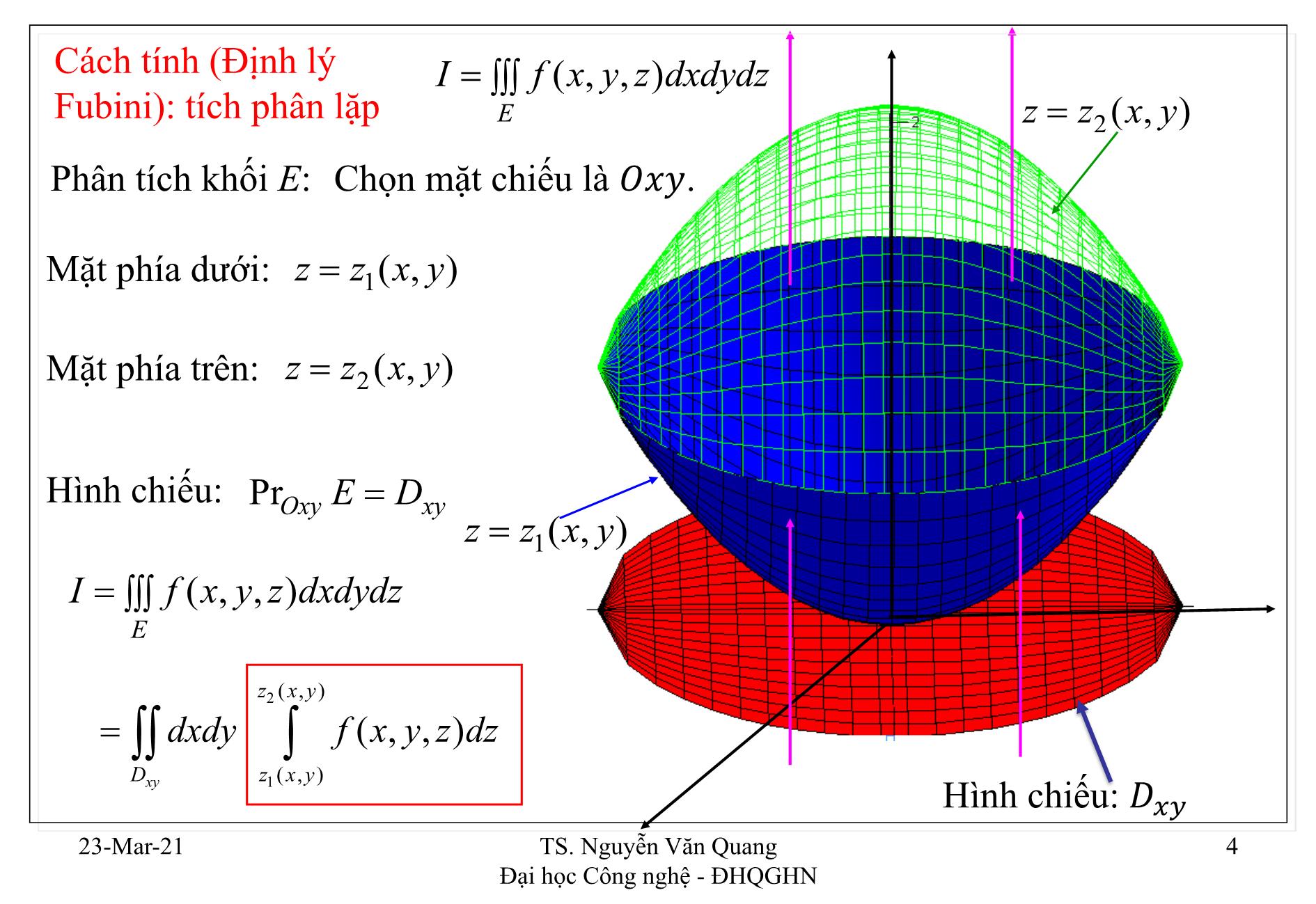
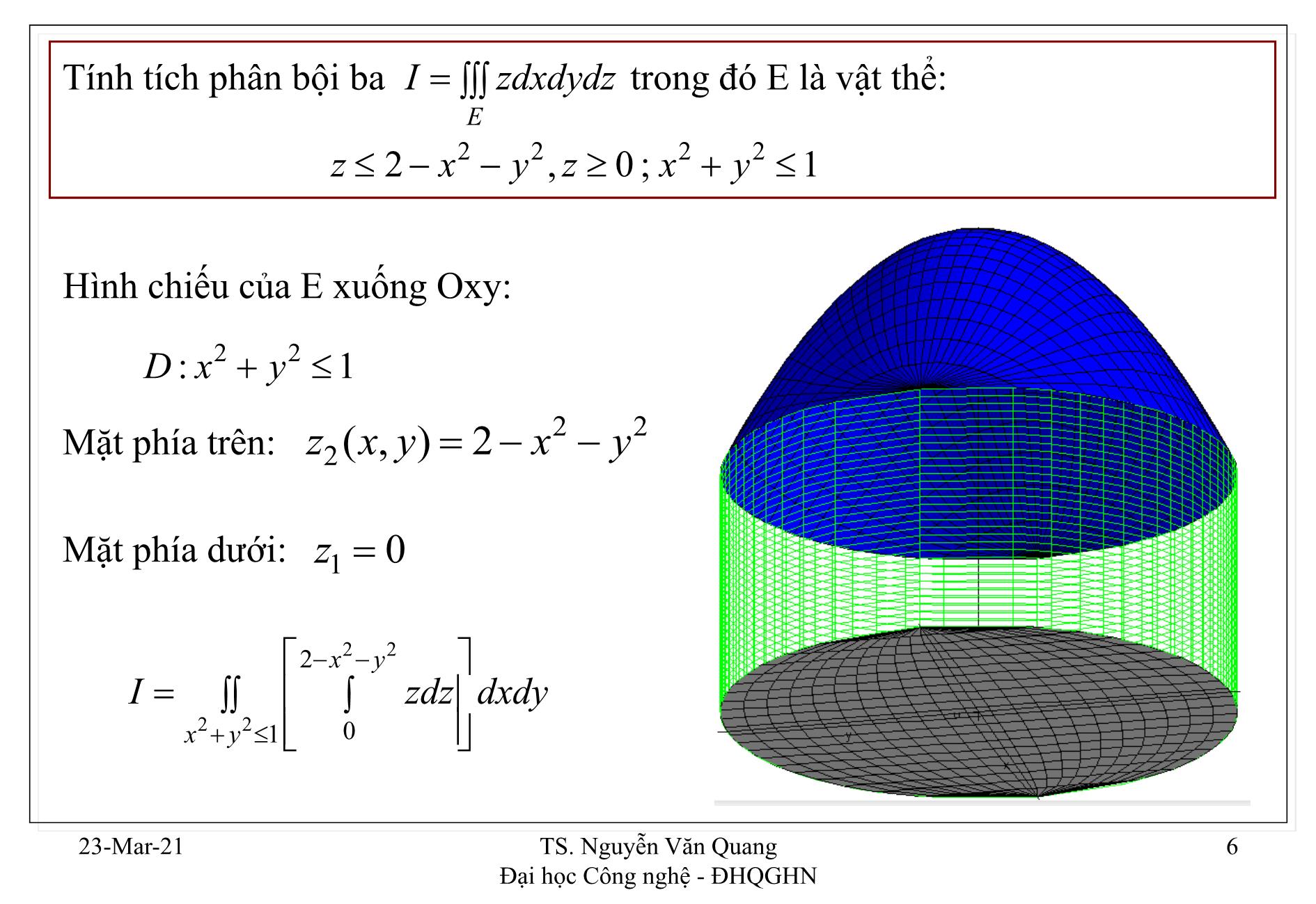
1. Định nghĩa, cách tính tích phân bội ba 
2. Hệ tọa độ trụ 
3. Hệ tọa độ cầu 
4. Ứng dụng hình học 
5. Ứng dụng cơ học 
Định nghĩa 
 f f (,,) x y z xác định trên vật thể đóng, bị chặn E . 
 Chia E một cách tùy ý ra thành n khối hình hộp nhỏ: EEE12, ,...,n .
 Thể tích tương ứng mỗi khối: VEVEVE ( 12 ), ( ),..., (n ).
 Trên mỗi khối E i lấy tuỳ ý một điểm M i ( x i , y i , z i ). 
 n
 Lập tổng Riemann: I n   f ()() M i V E i
 i 1
 II lim n , không phụ thuộc cách chia E, và cách lấy điểm Mi 
 n 
 I f(,,) x y z dxdydz
 E
 được gọi là tích phân bội ba của f = f(x,y,z) trên khối E. 
 23-Mar-21 TS. Nguyễn Văn Quang 2 
 Đại học Công nghệ - ĐHQGHN 
Tính chất 
 1) Hàm liên tục trên một khối đóng, bị chặn, thì khả tích trên miền này. 
 2) V E dxdydz 
 E
 3)  f ( x , y , z ) dxdydz f ( x , y , z ) dxdydz
 EE
 4) (f g ) dxdydz fdxdydz gdxdydz
 EEE
 5) Nếu E được chia làm hai khối E1 và E2 rời nhau: 
 fdxdydz fdxdydz fdxdydz
 EEE12
 6)  (,,),(,,)(,,)x y z E f x y z g x y z fdxdydz gdxdydz
 EE
 23-Mar-21 TS. Nguyễn Văn Quang 3 
 Đại học Công nghệ - ĐHQGHN 
Cách tính (Định lý 
 I f(,,) x y z dxdydz
Fubini): tích phân lặp E z z2 (,) x y
Phân tích khối E: Chọn mặt chiếu là . 
Mặt phía dưới: z z1(,) x y
Mặt phía trên: z z2 (,) x y
Hình chiếu: PrOxyED xy
 z z1(,) x y
 I f(,,) x y z dxdydz
 E
 z2 (,) x y
 dxdy f(,,) x y z dz
 Dxy z1 (,) x y
 Hình chiếu: 
 23-Mar-21 TS. Nguyễn Văn Quang 4 
 Đại học Công nghệ - ĐHQGHN 
Cách tính – Định lý Fubini (tích phân lặp) 
 Chú ý 
 • Tương tự ta có 2 công thức tích phân lặp khác, khi chiếu khối E 
 lên 2 mặt phẳng Oxz, Oyz. 
 • Thông thường, miền hình chiếu sẽ có biên là phương trình 
 của biên khối E nhưng không chứa . 
  Ta sẽ khử ở trong phương trình của biên khối E, hoặc tìm 
 phương trình nào không chứa của biên khối E. 
 23-Mar-21 TS. Nguyễn Văn Quang 5 
 Đại học Công nghệ - ĐHQGHN 
Tính tích phân bội ba I zdxdydz trong đó E là vật thể: 
 E
 z 2 x2 y 2 , z 0 ; x 2 y 2 1
Hình chiếu của E xuống Oxy: 
 D:1 x22 y
 22
Mặt phía trên: z2 ( x , y ) 2 x y
Mặt phía dưới: z 1 0
 2 xy22
 I zdz dxdy
 xy22 1 0
 23-Mar-21 TS. Nguyễn Văn Quang 6 
 Đại học Công nghệ - ĐHQGHN 
 2 xy22
 z2
 Id xdy
 22 2
 xy 1 0
 (2 xy2 2 ) 2
 I dxdy . Đổi sang hệ tọa độ cực. 
 xy22 1 2
 2
 2
 21 2 r 7 
 I d  r  dr 
 00 2 6
23-Mar-21 TS. Nguyễn Văn Quang 7 
 Đại học Công nghệ - ĐHQGHN 
Ví dụ 
 Tính tích phân bội ba I zdxdydz , trong đó E là vật thể giới hạn bởi: 
 E
 y 1 x , z 1 x2 , nằm trong góc phần tám thứ nhất. 
 Hình chiếu của E xuống Oxy: 
 Tam giác OAB. 
 2
 Mặt phía trên: z2 ( x , y ) 1 x
 Mặt phía dưới: z 1 0
 2
 1 x B 
 I dxdy zdz
 OAB 0
 A 
 23-Mar-21 TS. Nguyễn Văn Quang 8 
 Đại học Công nghệ - ĐHQGHN 
Ví dụ 
 1 x2
 I zdz dxdy
 A 
 OAB 0
 1 x2
 z2
 I dxdy
 OAB 2
 0
 2 B 
 1 x2 O 
 I dxdy
 OAB 2
 2
 2
 11 x 1 x 11
 dx dy 
 00 2 60
 23-Mar-21 TS. Nguyễn Văn Quang 9 
 Đại học Công nghệ - ĐHQGHN 
Ví dụ 
 Tính tích phân I (2 x 3 y ) dxdydz , trong đó E là vật thể giới hạn bởi: 
 E
 y x, z 1 y , x 0, z 0.
 Mặt phía trên: zy 1
 Mặt phía dưới: z 0
 Hình chiếu của E xuống Oxy: 
 23-Mar-21 TS. Nguyễn Văn Quang 10 
 Đại học Công nghệ - ĐHQGHN 
Ví dụ 
 1 y
 I 23 x y dz dxdy
 D 0
 I (2 x 3 y )z 1 y d xdy
 0
 D 
 I 2 x 3 y (1 y ) dxdy
 D
 11
 I dx 2 x 3 y (1 y ) dy
 0 x
 11
 I 
 60
 23-Mar-21 TS. Nguyễn Văn Quang 11 
 Đại học Công nghệ - ĐHQGHN 
Ví dụ 
 Tính tích phân I ( z 1) dxdydz , trong đó E là vật thể giới hạn bởi: 
 E
 x y2, z x , z 0, x 1.
 Mặt phía trên: zx 
 Mặt phía dưới: z 0
 Hình chiếu của E xuống Oxy: 
 23-Mar-21 TS. Nguyễn Văn Quang 12 
 Đại học Công nghệ - ĐHQGHN 
Ví dụ 
 x
 I ( z 1) dz dxdy
 D 0
 x
 z2
 I z dxdy
 D 2
 0
 x2
 I x dxdy
 D 2
 11 x2
 I dy x dx
 1 y2 2
 38
 I 
 35
 23-Mar-21 TS. Nguyễn Văn Quang 13 
 Đại học Công nghệ - ĐHQGHN 
Đổi biến tổng quát 
 Định lý: 
 Giả sử có phép đổi biến: = , 푣, 푤 , = , 푣, 푤 , = ( , 푣, 푤); sao cho 
 phép đổi biến này là 1-1 (có thể trừ trên biên), và 퐽 ≠ 0 (có thể 퐽 = 0 tại một số 
 điểm hữu hạn), khi đó: 
 ( , , ) =
 ( , 푣, 푤 , , 푣, 푤 , ( , 푣, 푤)). 퐽 . 푣 푤 
 푣푤
 Trong đó: 
 ′ ′ ′
 푣 푤
 휕( , , ) ′ ′ ′
 퐽 = = 푣 푤 
 휕( , 푣, 푤) ′ ′ ′
 푣 푤
 23-Mar-21 TS. Nguyễn Văn Quang 14 
 Đại học Công nghệ - ĐHQGHN 
Định nghĩa 
 z Điểm M(x,y,z) trong hệ trục tọa độ Oxyz. 
 M được xác định duy nhất bởi bộ (rz , , ).
 (,,)rz được gọi là hệ tọa độ trụ của điểm M. 
 M(,,) x y z Công thức đổi biến từ tọa độ Decasters sang 
 tọa độ trụ: 
 xr cos 
 yr sin 
 z 
 zz 
 y 
 r xrz x x 
 J y y y r
 x rz 
 M1( x , y ,0)
 zrz z z 
 23-Mar-21 TS. Nguyễn Văn Quang 15 
 Đại học Công nghệ - ĐHQGHN 
Đổi biến sang tọa độ trụ. I f(,,) x y z dxdydz
 xr cos E
 yr sin Mặt phía dưới: z z1(,) r 
 zz 
 z z(,) r 
 2 Mặt phía trên: z z2 (,) r 
 Hình chiếu: D 
 Xác định cận r , của D: 
 12 
 z z1(,) r D : 
 r12 r r
 2r 2 z 2 (,) r
 Id dr f( r cos , r sin , z ) r  dz
 1r 1 z 1(,) r
 23-Mar-21 TS. Nguyễn Văn Quang 16 
 Đại học Công nghệ - ĐHQGHN 
 22
 Tính tích phân I x y dxdydz , trong đó E là vật thể giới hạn bởi: 
 E
 z 4, z 1 x2 y 2 , x 2 y 2 1.
Mặt phía trên: z 4
Mặt phía dưới: zr 1 2
Hình chiếu xuống Oxy: D :1 x22 y
 02 
 D : 
 01 r
 2 1 4
I d dr r r  dz
 001 r2
 21 4 21 
 2 22 12 
I d dr r z d (3 r ) r dr 
 1 r2
 00 00 5
 23-Mar-21 TS. Nguyễn Văn Quang 17 
 Đại học Công nghệ - ĐHQGHN 
 Tính tích phân I zdxdydz , trong đó E là vật thể giới hạn bởi: 
 E
 z x2 y 2, z 2 x 2 y 2 , x 2 y 2 1.
 Mặt phía trên: zr 2 2
 Mặt phía dưới: zr 2
 Hình chiếu của E xuống O : 
 D:1 x22 y
 Cận của D: 
 02 
 D : 
 01 r
23-Mar-21 TS. Nguyễn Văn Quang 18 
 Đại học Công nghệ - ĐHQGHN 
 2
 2 2 r
 2 1 2 r 21 z2
 I d dr z r  dz d r dr 3 
 00 2 2
 r 00 r2
 22 22
Tính tích phân I x z dxdydz , trong đó E: 2y x z , y 2.
 E
Chiếu xuống O . 
Mặt trên: y 2
 r2
Mặt dưới: y 
 2
Hình chiếu: D:4 x22 z
 y 
 2 2 2
 2 16 
I d d r r r dy 
 00r2 /2 3
23-Mar-21 TS. Nguyễn Văn Quang 19 
 Đại học Công nghệ - ĐHQGHN 
Định nghĩa 
 Điểm ( , , ) trong hệ trục tọa độ O . 
 z M được xác định duy nhất bởi bộ ( , , ).
 (,,) được gọi là hệ tọa độ cầu của điểm M. 
 M(,,) x y z 
 Công thức đổi biến sang tọa độ cầu: 
 x sin   cos 
 y sin   sin 
 z cos z  cos
 
 y 
 x x x  
 J y y y J 2 sin
 r sin 
 z z z  
x 
 M1( x , y ,0)
 23-Mar-21 TS. Nguyễn Văn Quang 20 
 Đại học Công nghệ - ĐHQGHN 
Định nghĩa 
 Giả sử trong tọa độ cầu, vật thể E được giới hạn bởi: 
 12  
 12 
 12 
 I f(,,) x y z dxdydz
 E
  
 2 2 2 2
 d d f( sin  cos , sin  sin , cos )  sni  d
 1 1 1
 Chú ý: 0  
 02 hay 
 0 
 23-Mar-21 TS. Nguyễn Văn Quang 21 
 Đại học Công nghệ - ĐHQGHN 
 2 2 2
Tính tích phân I x y z dxdydz , trong đó E là vật thể giới hạn bởi: 
 E
 z x2 y 2,. x 2 y 2 z 2 z
 x sin   cos 
Đổi sang tọa độ cầu: y sin   sin 
 z  cos
Ta có: x2 y 2 z 2 z  cos
 z x22 y  
 4
 23-Mar-21 TS. Nguyễn Văn Quang 22 
 Đại học Công nghệ - ĐHQGHN 
 , const const 0,2 
  0,cos   0, 4  0, 4
  0,cos   0,cos 
23-Mar-21 TS. Nguyễn Văn Quang 23 
 Đại học Công nghệ - ĐHQGHN 
 Xác định cận: 0 
 4
 02 
 0  cos
 / 4 2 cos 
 2 12
 I d d  sin  d 
 0 0 0 10 80
23-Mar-21 TS. Nguyễn Văn Quang 24 
 Đại học Công nghệ - ĐHQGHN 
 Tính tích phân I zdxdydz , trong đó E là vật thể giới hạn bởi: 
 E
 z x2 y 2, x 2 y 2 z 2 1.
 x sin   cos z 
Đổi sang tọa độ cầu: y sin   sin 
 z  cos
 3 
 Xác định cận:  
 4
 02 y 
 01 
 2 1
 2 x 
I d d cos   sin  d 
 3 / 4 00
 8
 23-Mar-21 TS. Nguyễn Văn Quang 25 
 Đại học Công nghệ - ĐHQGHN 
 Tính tích phân I () y z dxdydz , trong đó E là vật thể giới hạn bởi: 
 E
 z 0, x2 y 2 z 2 2 y ( z 0)
Cách 1: 
 x sin   cos z 
Đổi sang tọa độ cầu: y sin   sin 
 z  cos y 
Xác định cận:  
 2 x 
 0 
 0 2sin   sin 
 2sin  sin
 2 5 
 I d d ( sin  sin + cos  )  sin  d 
 / 2 0 0 12
 23-Mar-21 TS. Nguyễn Văn Quang 26 
 Đại học Công nghệ - ĐHQGHN 
Cách 2: 
 z 
 Đổi sang tọa độ cầu mở rộng: 
 Gốc tọa độ dời về đây 
 x sin   cos 
 y 1  sin  sin 
 z  cos
 y 
 Xác định cận:  
 2
 02 
 01 x 
 21
 2 5 
 I d d (1 sin  sin + cos)   sni  d 
 / 2 0 0 12
 23-Mar-21 TS. Nguyễn Văn Quang 27 
 Đại học Công nghệ - ĐHQGHN 
 ()x2 y 2 z 2 3/ 2
 Tính tích phân I e dxdydz , trong đó E là vật thể giới hạn bởi: 
 E
 y 0, x2 y 2 z 2 1 ( y 0)
 x sin   cos z 
Đổi sang tọa độ cầu: y sin   sin 
 z  cos
 Xác định cận: 0  
 2 
 y 
 01 
 x 
 21
 3 2 2(e 1) 
 I d d e  sin  d 
 00 3
 23-Mar-21 TS. Nguyễn Văn Quang 28 
 Đại học Công nghệ - ĐHQGHN 
Tính tích phân I zdxdydz , trong đó E là vật thể giới hạn bởi: 
 E
 z 1, x2 y 2 z 2 2 z ( z 1)
 x sin   cos 
Đổi sang tọa độ cầu: y sin   sin 
 z  cos
Xác định cận: 0 
 2
 02 
 0 ?
Phải chia khối E ra làm 2 khối. Việc tính toán rất phức tạp. 
23-Mar-21 TS. Nguyễn Văn Quang 29 
 Đại học Công nghệ - ĐHQGHN 
Đổi sang tọa độ cầu mở rộng: 
 x sin   cos Gốc tọa độ dời về đây 
 y  sin  sin 
 z 1  cos
 Xác định cận:  
 2
 02 
 01 
 21
 2 5 
 I d d (1 cos )  sin  d 
 / 2 0 0 12
 23-Mar-21 TS. Nguyễn Văn Quang 30 
 Đại học Công nghệ - ĐHQGHN 
 1
 Tính tích phân I dxdydz , trong đó E là vật thể giới hạn bởi: 
 E xy22 
 z 0, x2 y 2 z 2 4, x 2 y 2 1 ( z 0)
Sử dụng tọa độ cầu, việc tính toán phức tạp 
hơn nhiều. 
 xr cos 
Đổi sang tọa độ trụ: yr sin 
 zz 
Xác định cận: 02 
 01 r
 04 zr 2
 2 1 4 r2 r 2 3 3 
 I d dr dz 
 0 0 0 r 3
 23-Mar-21 TS. Nguyễn Văn Quang 31 
 Đại học Công nghệ - ĐHQGHN 
Ví dụ 
 0 0 0
 Đổi sang tọa độ cầu rồi tính: I dx dy xdz
 2 44 x2 x 2 y 2
 Xác định vật thể E: Vẽ khối E: z y 
 20 x 
 x 
 2
 40 xy 
 22
 40 x y z 
 23-Mar-21 TS. Nguyễn Văn Quang 32 
 Đại học Công nghệ - ĐHQGHN 
Đổi biến sang tọa độ cầu: z y 
 x sin   cos 
 x 
 y sin   sin 
 z  cos
Xác định cận:  
 2
 3 
 2
 02 
 3 / 2 2
 2
I d d sin  cos  sin   d 
 / 2 0
 3 / 2 2 3 / 2
 221 2
I sin d   cos d   d  sindd  cos 
 / 2 0 4 /2
 23-Mar-21 TS. Nguyễn Văn Quang 33 
 Đại học Công nghệ - ĐHQGHN 
 2 2xx 2 4
 22
Đổi sang tọa độ trụ rồi tính: I dx dy z x y dz
 0 0 0
 z
Xác định vật thể E: Vẽ khối E: 
 02 x
 2
 02 y x x
 04 z
 y 
 y
 x 
 x
23-Mar-21 TS. Nguyễn Văn Quang 34 
 Đại học Công nghệ - ĐHQGHN 
Đổi biến sang tọa độ trụ: 
 z 
 xr cos 
 yr sin 
 zz 
Xác định cận: 0 
 2
 0 r 2cos 
 04 z
 / 22cos 4 y 
 I d dr z  r  r  dz
 0 0 0
 4
 /2 2cos 2
 2 z
 I d r dr
 2
 00 0
 128 x 
 I 
 9
 23-Mar-21 TS. Nguyễn Văn Quang 35 
 Đại học Công nghệ - ĐHQGHN 
Ứng dụng hình học của tích phân bội ba 
 Từ định nghĩa tích phân bội ba ta có công thức tính thể tích vật thể E: 
 VE dxdydz
 E
 Có thể sử dụng tích phân kép để tính thể tích vật thể. 
 Tuy nhiên trong một số trường hợp sử dụng tích phân bội ba tính nhanh hơn, 
 vì tích phân bội ba có cách đổi sang tọa độ trụ hoặc tọa độ cầu. 
 23-Mar-21 TS. Nguyễn Văn Quang 36 
 Đại học Công nghệ - ĐHQGHN 
 Tính thể tích vật thể E được giới hạn bởi: 
 x2 y 2 z 2 1; x 2 y 2 z 2 4, z x 2 y 2
V dxdydz 0 
 E 4
Sử dụng tọa độ cầu: 02 
 12 
 /4 22
 2
V  d d sin d 
 0 0 1
 (14 7 2) 
V 
 3
 Sử dụng tích phân kép, tính toán rất phức tạp !!! 
 23-Mar-21 TS. Nguyễn Văn Quang 37 
 Đại học Công nghệ - ĐHQGHN 
 Tính thể tích vật thể E được giới hạn bởi: x 22 y 2 x ; x z 3, x z 3
V dxdydz
 z 
 E xr cos 
Sử dụng tọa độ trụ: yr sin 
 zz 
 22
 0 r 2cos x 
 rcos 3 z 3 r cos
 y 
 /2 2cros 3 cos
 V  d dr r dz
 / 2 0r cos 3
 V 4 
 23-Mar-21 TS. Nguyễn Văn Quang 38 
 Đại học Công nghệ - ĐHQGHN 
 Tính thể tích vật thể E được giới hạn bởi: x 2 y 2 z 2 4; x 2 y 2 z 2 4 z
 V dxdydz
 E
Sử dụng tọa độ trụ: 
 02 
 03 r y 
 2 4 r22 z 4 r
 2 3 4 r2
 V  d dr r dz
 0024 r2 x 
 10 
 V Sử dụng tọa độ cầu tính phức tạp hơn nhiều. 
 3
 23-Mar-21 TS. Nguyễn Văn Quang 39 
 Đại học Công nghệ - ĐHQGHN 
Tính thể tích vật thể E được giới hạn bởi: y x 2 , y z 1, z 0. 
 1 y 111 y
 V dxdydz dz dxdy dx dy dz
 E Parabol 0 10x2
23-Mar-21 TS. Nguyễn Văn Quang 40 
 Đại học Công nghệ - ĐHQGHN