Bài giảng Đồ họa máy tính - Bài: Xác định mặt hiện (Visible surface determination) - Ma Thị Châu

 Đồ họa máy tính
 Xác định mặt hiện
 (Visible surface determination)
1 2/17/17
 Sự hữu hình của các đối tượng cơ bản
 l Chúng ta không muốn phí thời gian để hiển thị 
 những đối tượng không đóng góp vào bức ảnh cuối 
 cùng.
 l Một đối tượng có thể không hữu hình vì 3 lý do:
 – Nằm ngoài vùng hiển thị
 – Quay vào trong (back-facing)
 – Bị che bởi các đối tượng khác gần người quan sát hơn
 l Làm thế nào để loại bỏ chúng một cách hiệu quả?
 l Làm thế nào để xác định chúng một cách hiệu quả?
2 2/17/17
 Vấn đề hữu hình
 Hai vấn đề còn lại:
 (Chúng ta đã làm quen với clipping)
 • Loại bỏ các bề mặt hướng ra phía khác so với người quan sát.
 • Loại bỏ các bề mặt che bởi các đối tượng gần hơn.
3 2/17/17
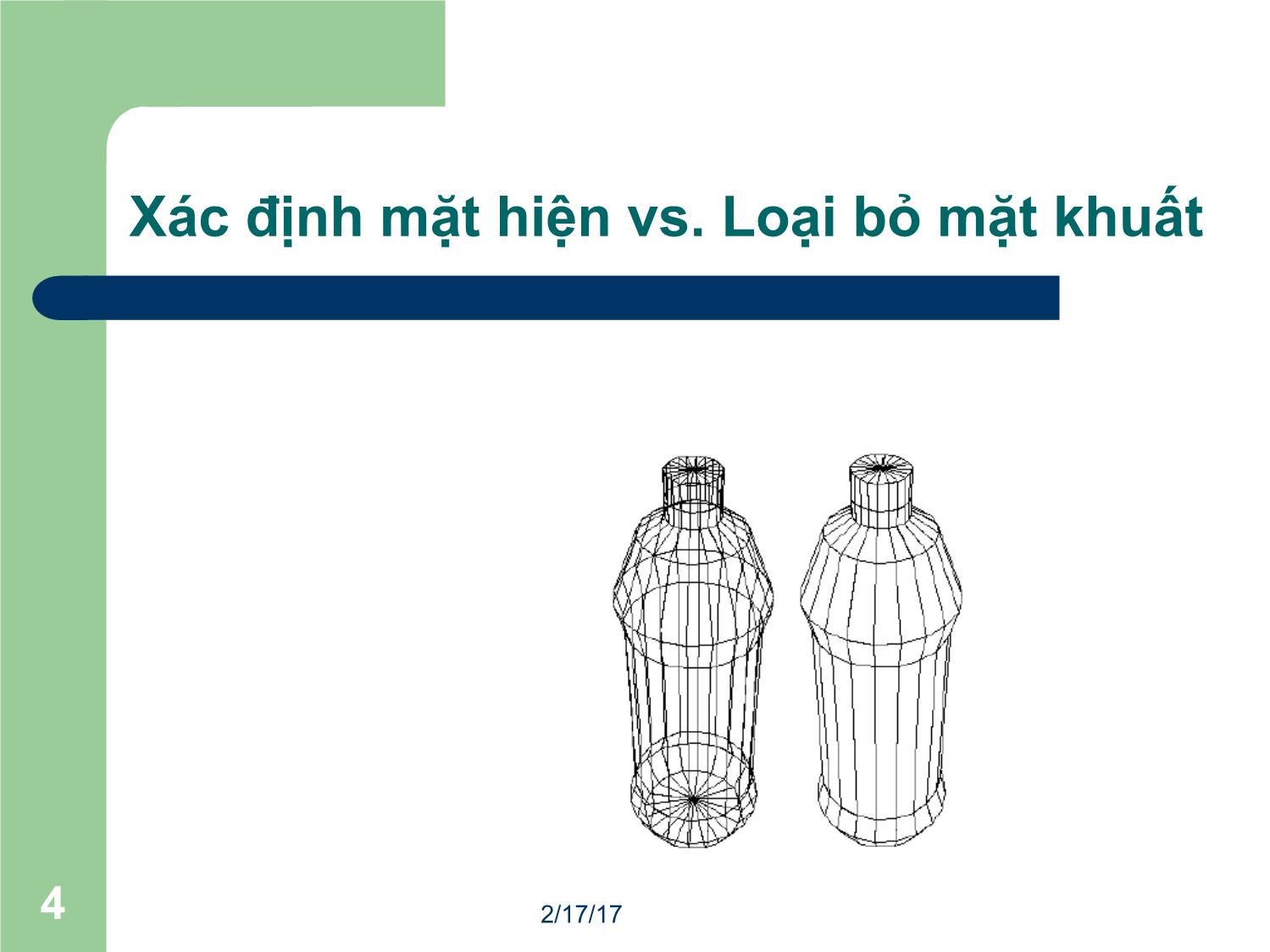
 Xác định mặt hiện vs. Loại bỏ mặt khuất
4 2/17/17
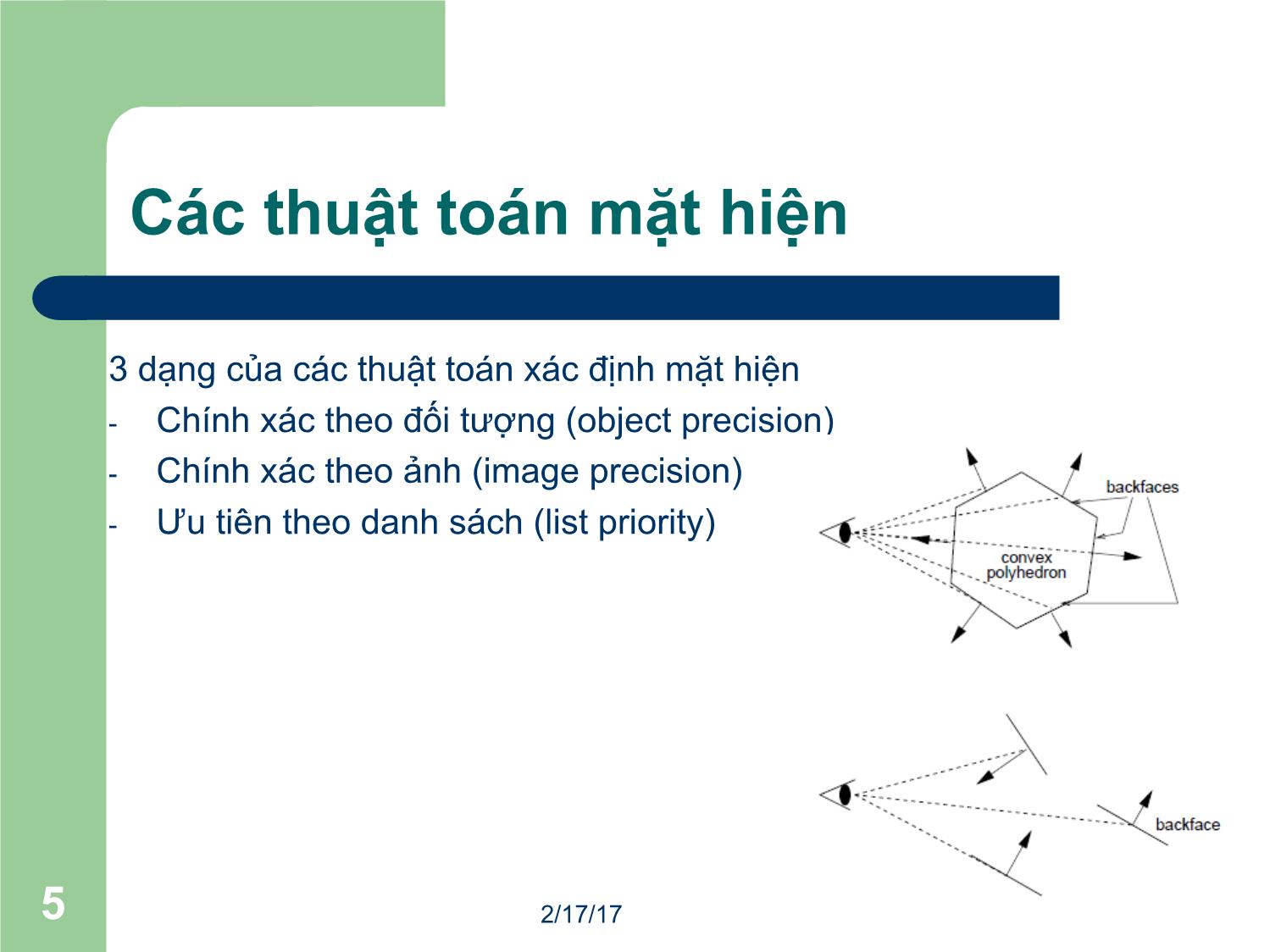
 Các thuật toán mặt hiện
 3 dạng của các thuật toán xác định mặt hiện
 - Chính xác theo đối tượng (object precision)
 - Chính xác theo ảnh (image precision)
 - Ưu tiên theo danh sách (list priority)
5 2/17/17
 Các thuật toán mặt hiện
 Loại bỏ/Xác định Mặt/đoạn Ẩn/hiện
 l Yêu cầu
 – Có thể xử lý các tập đối tượng khác nhau
 – Có thể xử lý một lượng lớn các đại lượng hình học
 Phân loại: Sutherland, Sproull, Schumacher (1974):
 l Không gian vật thể
 – Tính toán hình học liên quan đến đa giác
 – Độ chính xác số thực
 – Thường xử lý cảnh vật theo thứ tự các vật thể
 l Không gian ảnh
 – Visibility at pixel samples
 – Độ chính xác số nguyên
 – Thường xử lý cảnh vật theo thứ tự ảnh
6 2/17/17
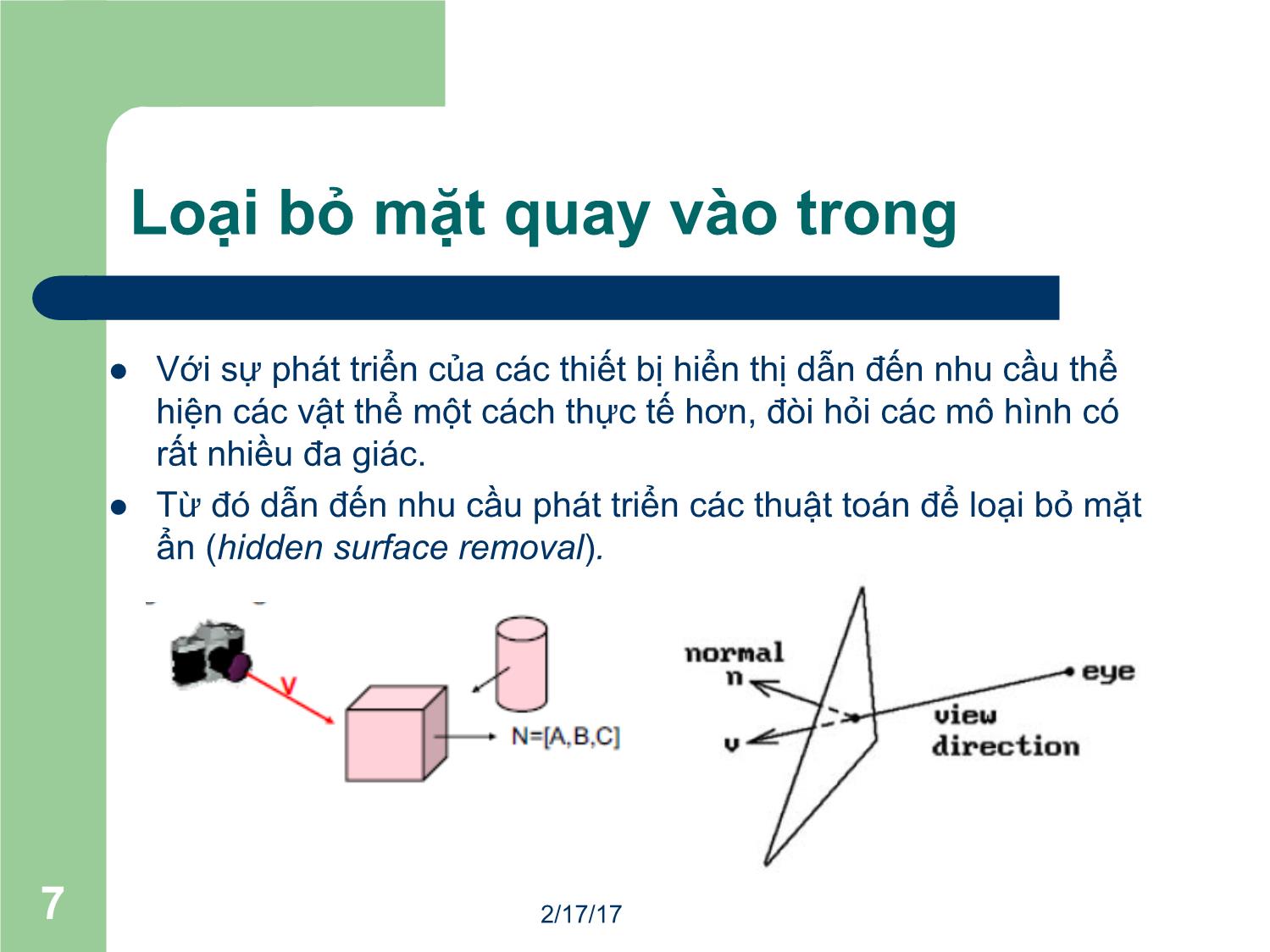
 Loại bỏ mặt quay vào trong
 l Với sự phát triển của các thiết bị hiển thị dẫn đến nhu cầu thể 
 hiện các vật thể một cách thực tế hơn, đòi hỏi các mô hình có 
 rất nhiều đa giác.
 l Từ đó dẫn đến nhu cầu phát triển các thuật toán để loại bỏ mặt 
 ẩn (hidden surface removal).
7 2/17/17
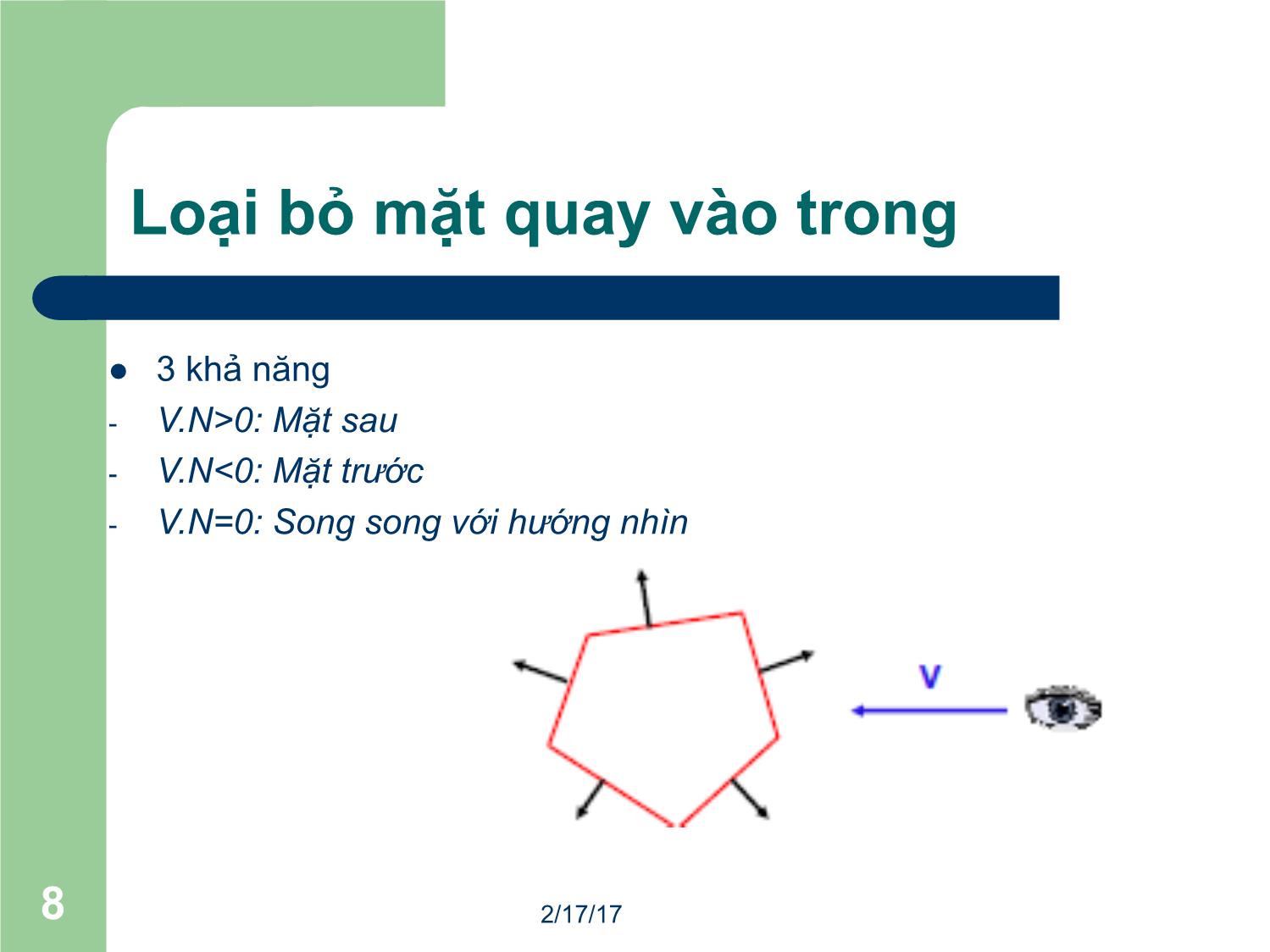
 Loại bỏ mặt quay vào trong
 l 3 khả năng
 - V.N>0: Mặt sau
 - V.N<0: Mặt trước
 - V.N=0: Song song với hướng nhìn
8 2/17/17
 Loại bỏ mặt quay vào trong
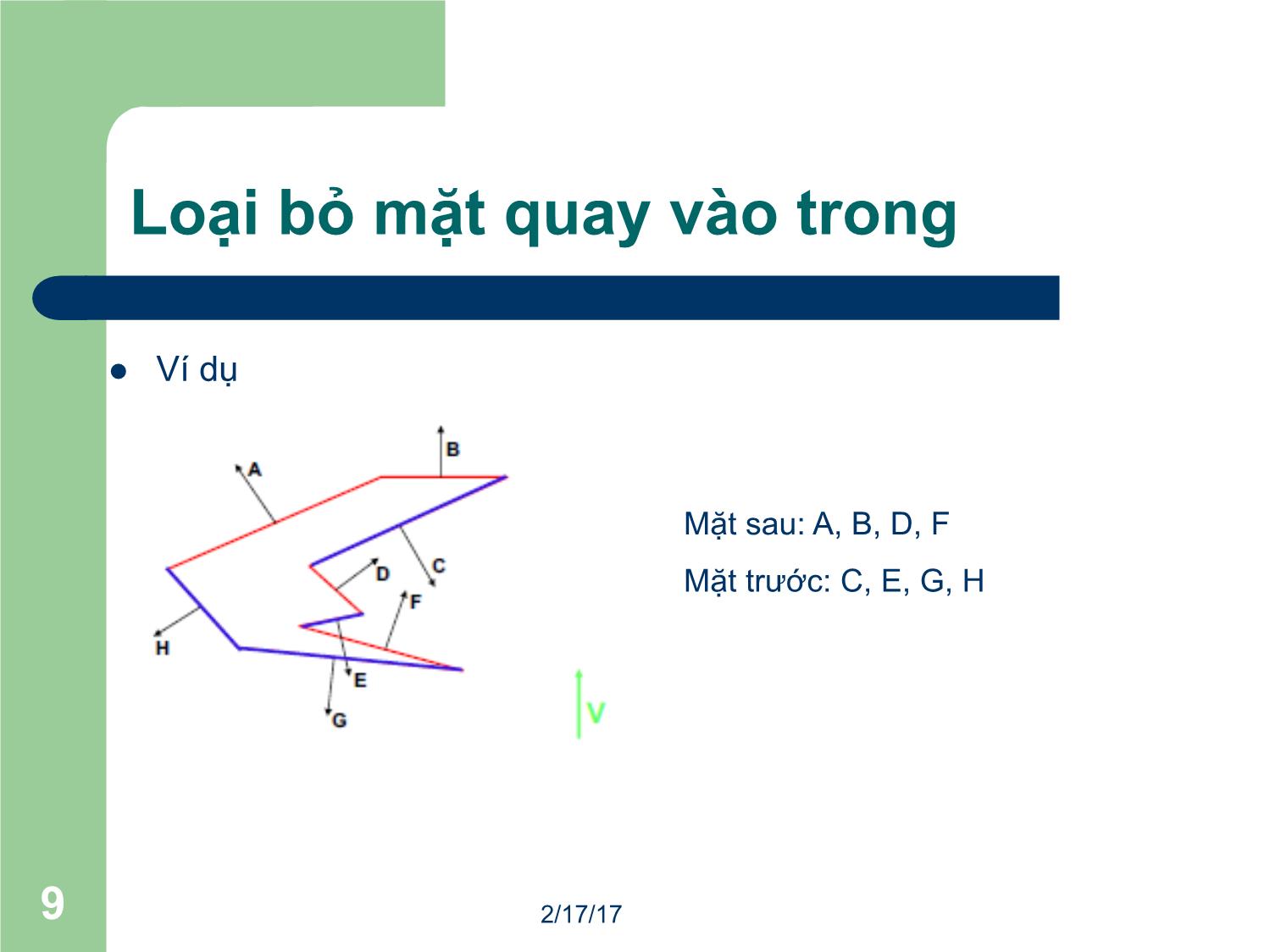
 l Ví dụ
 Mặt sau: A, B, D, F
 Mặt trước: C, E, G, H
9 2/17/17
 Thuật toán ưu tiên theo danh sách
 Schumacker
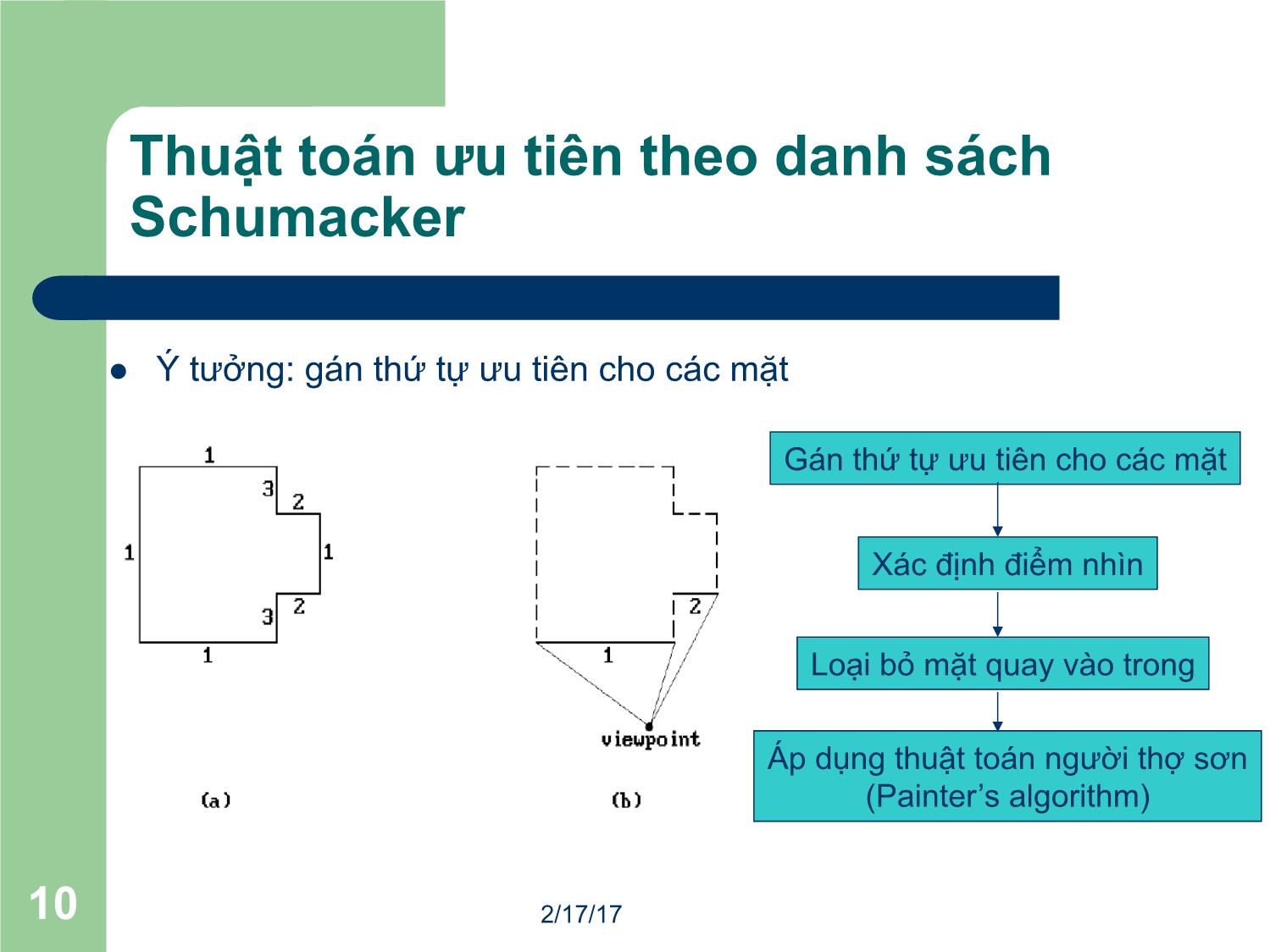
 l Ý tưởng: gán thứ tự ưu tiên cho các mặt
 Gán thứ tự ưu tiên cho các mặt
 Xác định điểm nhìn
 Loại bỏ mặt quay vào trong
 Áp dụng thuật toán người thợ sơn
 (Painter’s algorithm)
10 2/17/17
 Thuật toán người thợ sơn
 l Vẽ các bề mặt theo thứ tự 
 từ sau đến trước – các đa 
 giác gần hơn sẽ được vẽ đề 
 lên đa giác xa hơn.
 l Hỗ trợ tính trong suốt.
 l Vấn đề mấu chốt là xác định 
 thứ tự.
 l Không phai lúc nào cũng 
 thực hiện được.
11 2/17/17
 Thuật toán người thợ sơn
12 2/17/17
 Gán thứ tự ưu tiên?
 l Sắp xếp các đối tượng theo chiều sâu
 à Thuật toán Newell-Newell-Sancha
13 2/17/17
 Sắp xếp theo chiều sâu Newell-Newell-Sancha
 l Sắp xếp các đối tượng theo chiều sâu dựa trên giá trị z
 - Xét P – đa giác xa nhất so với điểm nhìn và đa giác tiếp theo Q
 - P&Q tách biệt nhau về độ sâu
 - Đúng: P không bao giờ che khuất mặt nào à vẽ P
 - Sai: Xét các tập đa giác {QS} giao P theo chiều sâu
14 2/17/17
 Sắp xếp theo chiều sâu Newell-Newell-Sancha
 l {QS} giao P? à Các phép thử:
 1. Có thể phân tách P và {QS} theo x được 
 không?
 2. Có thể phân tách P và {QS} theo y được 
 không?
15 2/17/17
 Sắp xếp theo chiều sâu Newell-Newell-Sancha
 l {QS} giao P? à Các phép thử:
 3. P có nằm ở phần xa của {QS} không?
 (all vertices of P lie deeper than the plane of Q)
 4. {QS} có nằm ở phần gần của P không?
 (all vertices of Q lie closer to the viewpoint than the plane of P)
16 2/17/17
 Sắp xếp theo chiều sâu Newell-Newell-Sancha
 l {QS} giao P? à Các phép thử:
 5. Hình chiếu của P và {QS} có rời rạc không?
 nếu tất cả các câu trả lời là không
 à Hoán đổi P với một mặt trong {QS}: lặp lại 
 các phép thử
17 2/17/17
 Sắp xếp theo chiều sâu Newell-Newell-Sancha
 l Vòng lặp vô hạn
18 2/17/17
 Cây BSP (Binary Space Partitioning)
 •2 bước:
 -Chuyển danh sách đa giác sang 5
 dạng cấu trúc cây nhị phân (cây 
 BSP) 2
 -Duyệt cây BSP và vẽ các đa giác 
 3
 ra bộ đệm khung theo thứ tự từ sau 1 4
 ra trước
 View of scene from above
19 2/17/17
 Cây BSP 
 •Mặt phẳng phân tách: sao cho 
 không có đa giác nào nằm ở nửa 5
 không gian chứa điểm nhìn bị một 
 đa giác nằm ở nửa không gian còn 2
 lại che khuất
 3
 1 4
 5 đa giác
 các mũi tên chỉ về phía có điểm nhìn
20 2/17/17