Bài giảng Đồ họa máy tính - Bài: Vẽ đường thẳng và đường tròn - Ma Thị Châu

 Đồ họa máy tính
 Vẽ đường thẳng và đường tròn
1 2/17/17 Ma Thị Châu - Bộ môn KHMT
 Hướng tới một đường thẳng lý tưởng
 l Chúng ta chỉ có thể vẽ xấp xỉ đường thẳng một cách 
 rời rạc
 l Chiếu sáng các điểm gần nhất với đường thẳng 
 thực tế trong trường hợp chỉ có hai cách thể hiện 
 một điểm:
 – Điểm được thắp sáng hoặc không thắp sáng
2 2/17/17 Ma Thị Châu - Bộ môn KHMT
 Thế nào là một đường thẳng lý tưởng
 l Trông phải thẳng và liên tục
 – Trong máy tính chỉ có thể được như vậy với các đường 
 thẳng song song với trục tọa độ hoặc có góc 45o với trục tọa 
 độ
 l Phải đi qua hai điểm đầu và cuối
 l Phải có mật độ và cường độ sáng đều
 – Đều trên một đường thẳng và đều trên tất cả các đường 
 thẳng
 l Thuật toán vẽ phải hiệu quả và có thể thực hiện 
 nhanh
3 2/17/17 Ma Thị Châu - Bộ môn KHMT
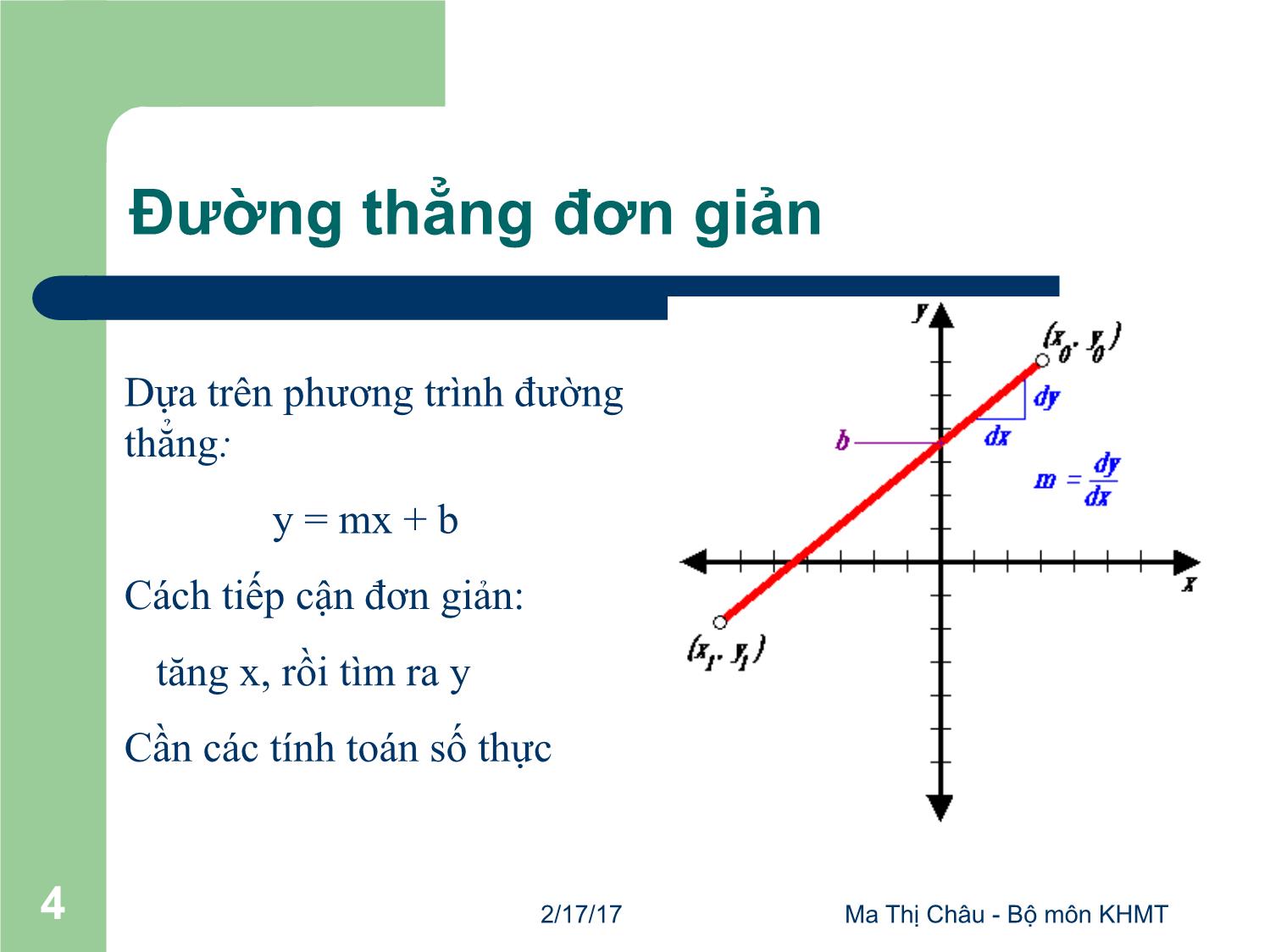
 Đường thẳng đơn giản
 Dựa trên phương trình đường 
 thẳng:
 y = mx + b
 Cách tiếp cận đơn giản:
 tăng x, rồi tìm ra y
 Cần các tính toán số thực
4 2/17/17 Ma Thị Châu - Bộ môn KHMT
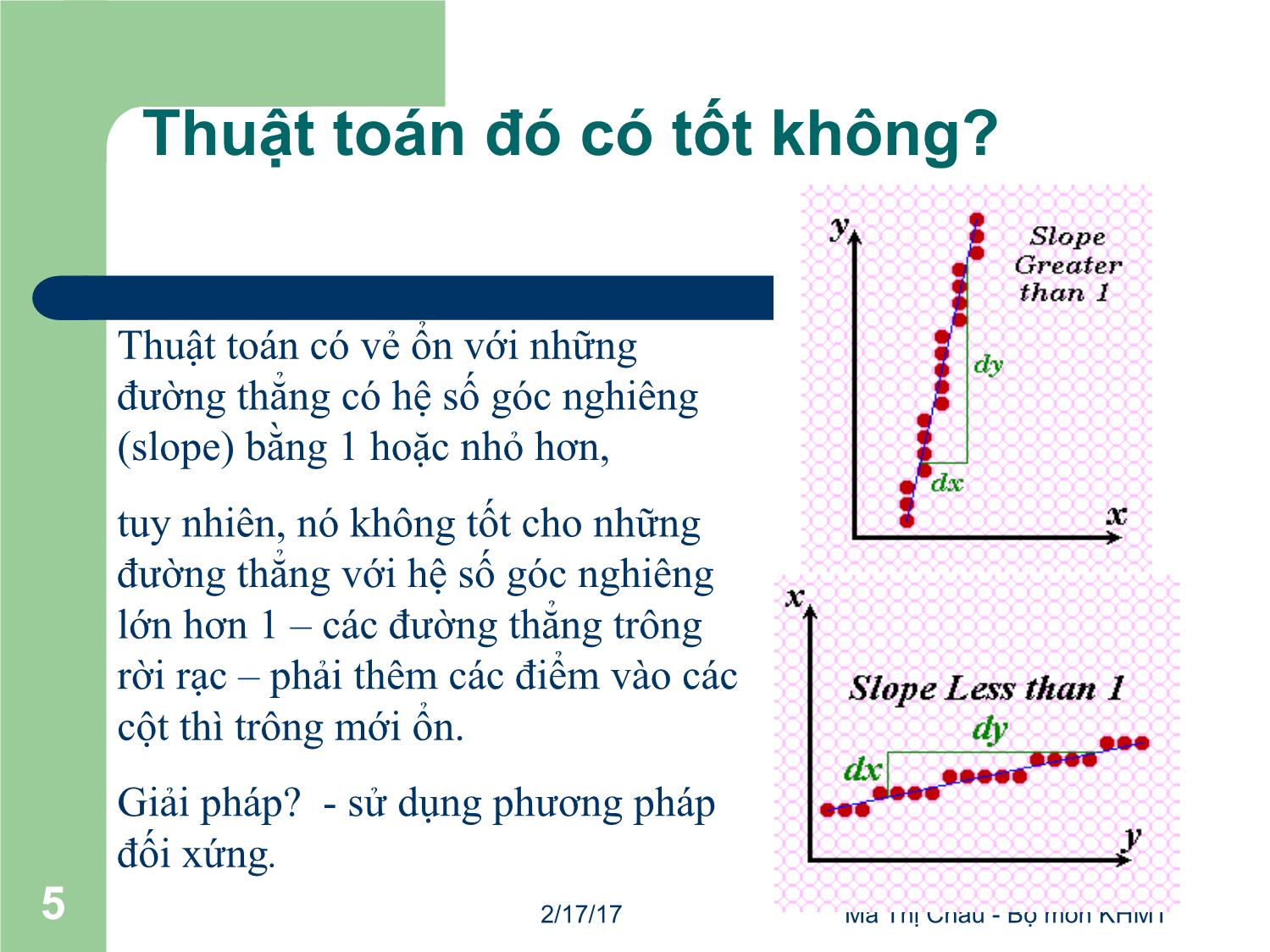
 Thuật toán đó có tốt không?
 Thuật toán có vẻ ổn với những 
 đường thẳng có hệ số góc nghiêng 
 (slope) bằng 1 hoặc nhỏ hơn,
 tuy nhiên, nó không tốt cho những 
 đường thẳng với hệ số góc nghiêng 
 lớn hơn 1 – các đường thẳng trông 
 rời rạc – phải thêm các điểm vào các 
 cột thì trông mới ổn.
 Giải pháp? - sử dụng phương pháp 
 đối xứng.
5 2/17/17 Ma Thị Châu - Bộ môn KHMT
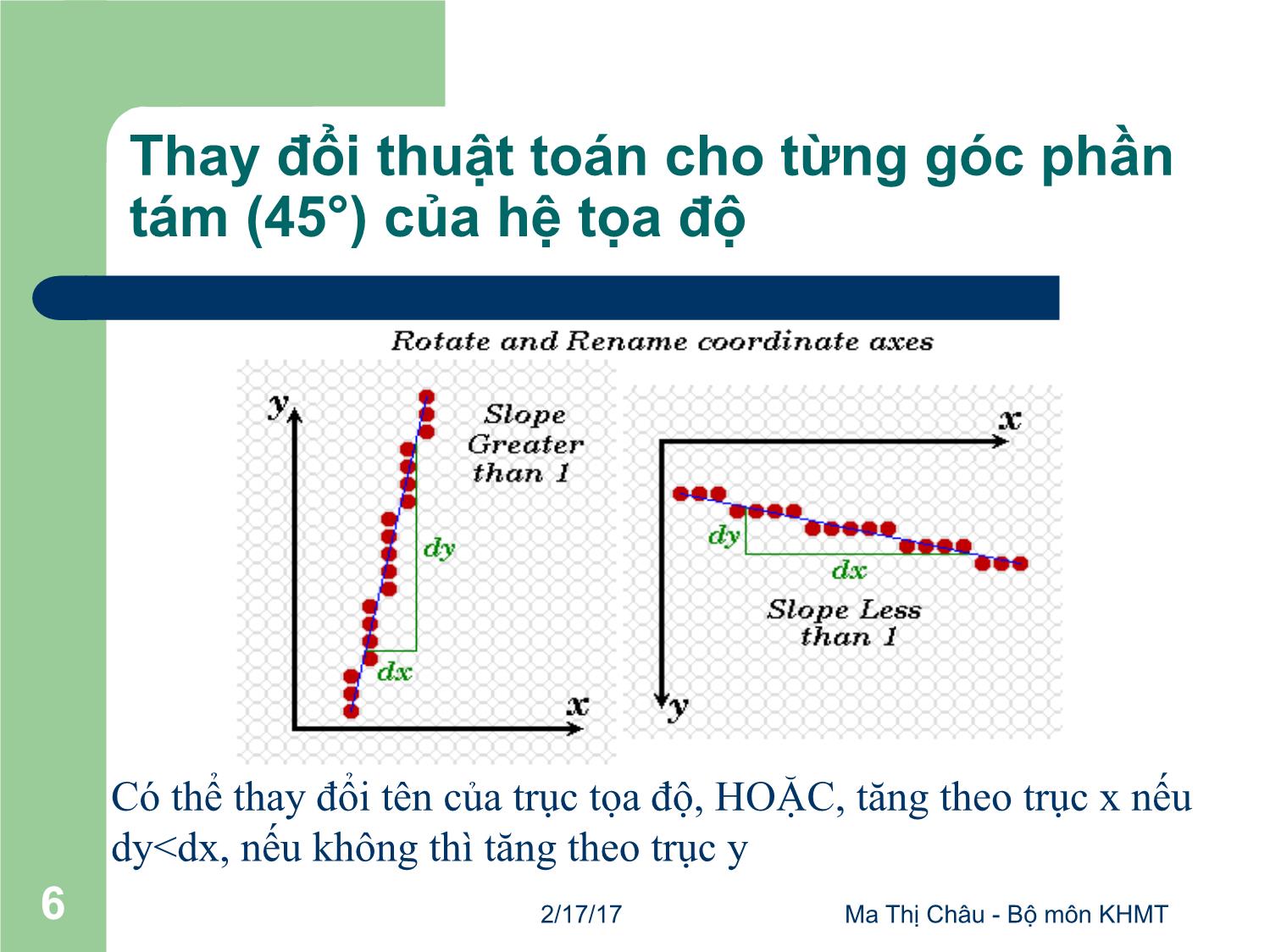
 Thay đổi thuật toán cho từng góc phần 
 tám (45°) của hệ tọa độ
 Có thể thay đổi tên của trục tọa độ, HOẶC, tăng theo trục x nếu 
 dy<dx, nếu không thì tăng theo trục y
6 2/17/17 Ma Thị Châu - Bộ môn KHMT
 Thuật toán DDA
 l DDA = Digital Differential Analyser
 (Phân tích vi phân số hóa)
 l Xét đường thẳng theo phương trình tham số theo t:
 x(t) = x + t(x - x )
 Start point - (x1, y1) 1 2 1
 End point - (x , y )
 2 2 y(t) = y1 + t(y2 - y1)
7 2/17/17 Ma Thị Châu - Bộ môn KHMT
 x(t) = x + t(x - x )
 Thuật toán DDA 1 2 1
 y(t) = y1 + t(y2 - y1)
 l Bắt đầu với t = 0 dx
 x = x +
 l Tại mỗi bước, tăng t một lượng moi cu dt
 dy
 dt y = y +
 moi cu dt
 l Chọn giá trị thích hợp cho dt
 l Sao cho không bỏ mất điểm nào:
 dx dy
 – Nghĩa là: < 1 và <1
 dt dt
 l Chọn dt là giá trị max của dx và dy
8 2/17/17 Ma Thị Châu - Bộ môn KHMT
 Thuật toán DDA
 line(int x1, int y1, int x2, int y2)
 { n - range of t.
 float x,y;
 int dx = x2-x1, dy = y2-y1;
 int n = max(abs(dx),abs(dy));
 float dt = n, dxdt = dx/dt, dydt = dy/dt;
 x = x1;
 y = y1;
 while( n-- ) {
 point(round(x),round(y));
 x += dxdt;
 y += dydt;
 }
9 } 2/17/17 Ma Thị Châu - Bộ môn KHMT
 Thuật toán DDA
 l Vẫn còn sử dụng rất nhiều phép toán số 
 thực.
 – 2 phép làm tròn và hai phép cộng số thực.
 l Liệu có cách nào đơn giản hơn không?
 l Có cách nào mà chúng ta chỉ cần dùng các 
 phép toán số nguyên?
 – Như vậy sẽ có thể cài đặt dễ dàng trên máy tính 
 hiện thời và có thể chạy rất nhanh.
10 2/17/17 Ma Thị Châu - Bộ môn KHMT