Bài giảng Đồ họa máy tính - Bài: Đường cong và bề mặt II - Mai Thị Châu
Bề mặt cong
l Có thể mở rộng khái niệm đoạn cong cho các bề
mặt cong.
l Các bề mặt cong được xác định bởi công thức tham
số của hai biến, s và t.
l Nghĩa là, một bề mặt cong là một tập hợp các
đường cong tham số
l Xấp xỉ bằng một lưới đa giác. Khi vẽ, càng giảm nhỏ
bước của s và t càng cho độ chính xác cao

Trang 1

Trang 2

Trang 3

Trang 4
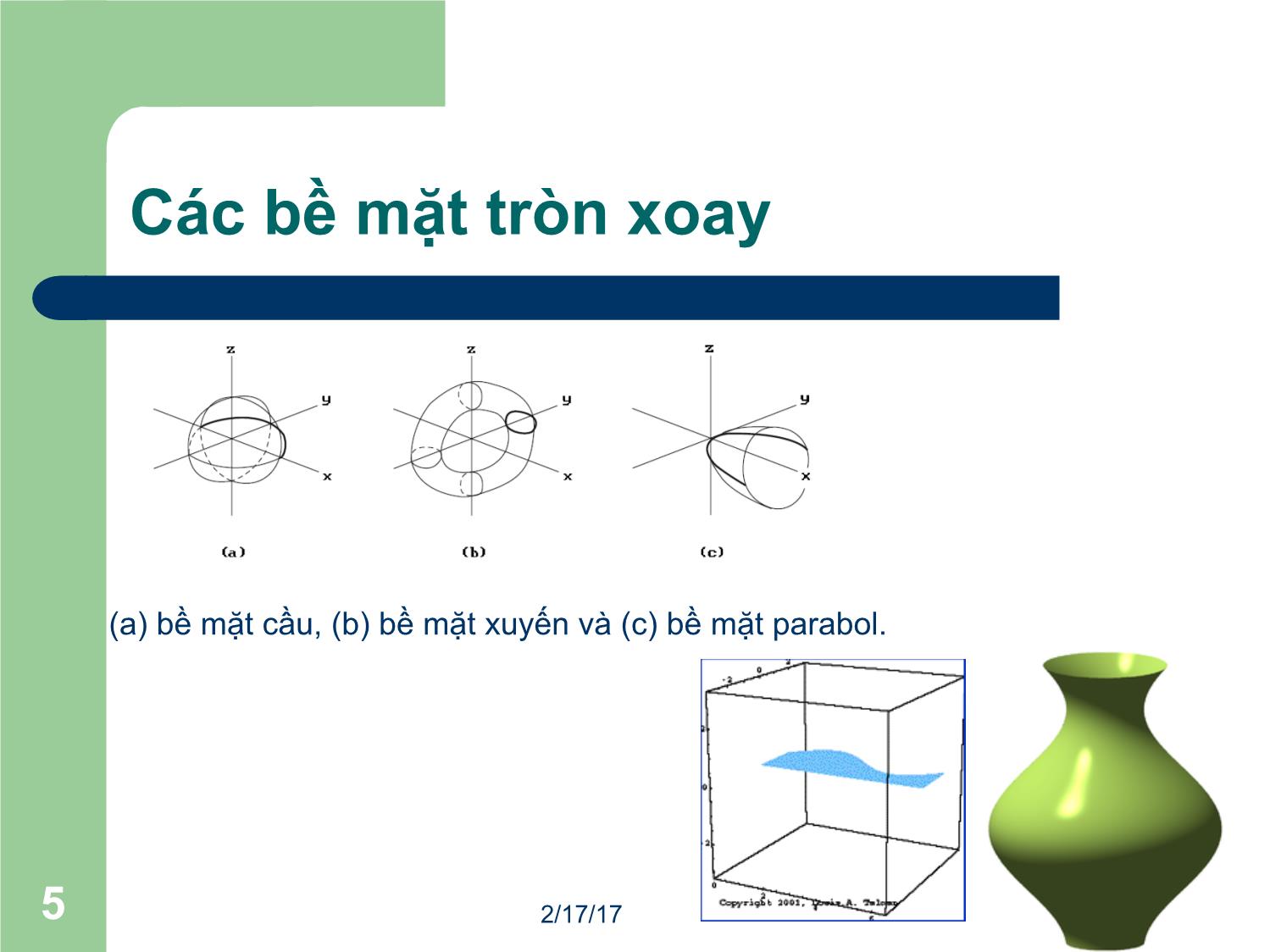
Trang 5
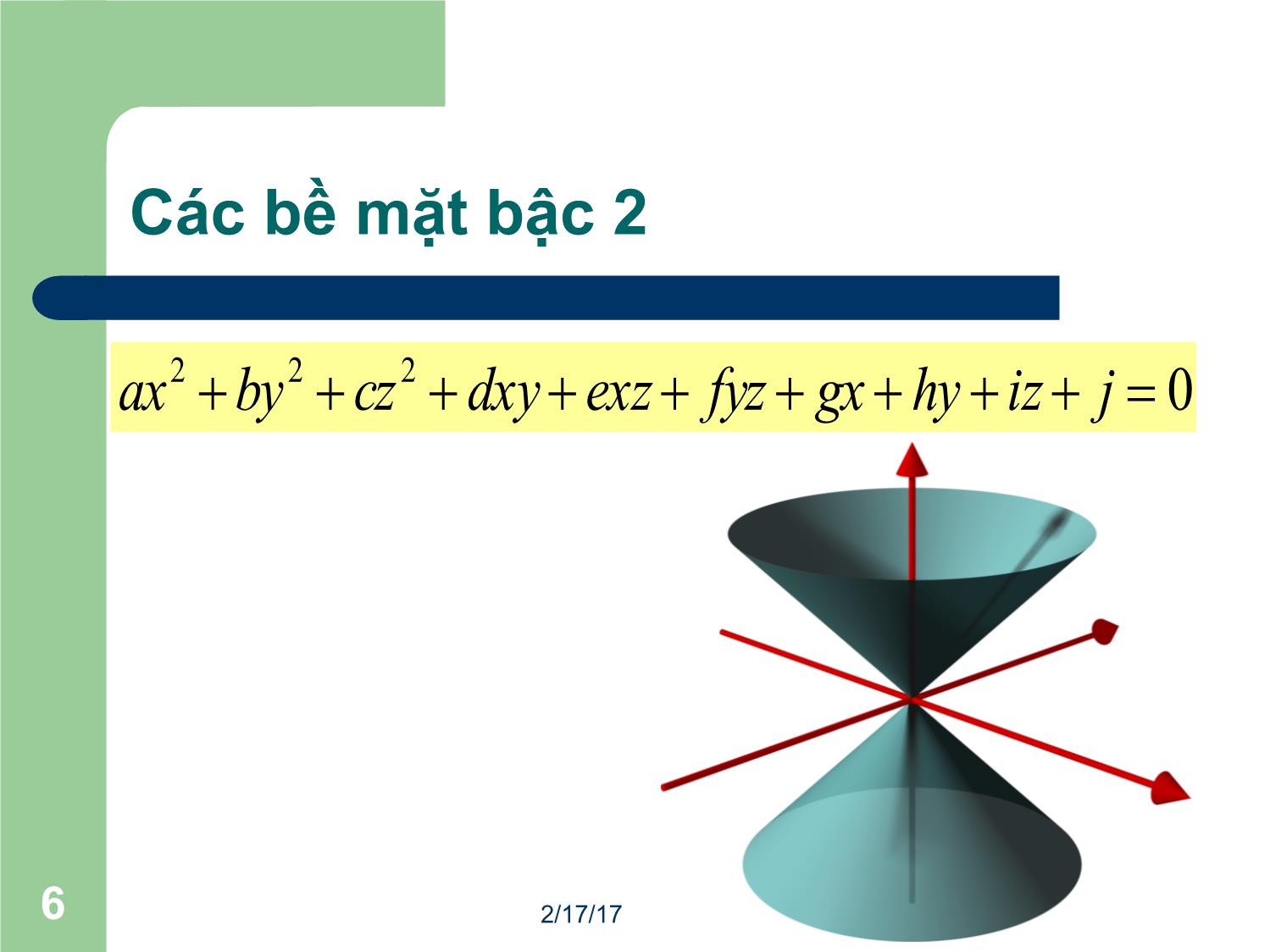
Trang 6
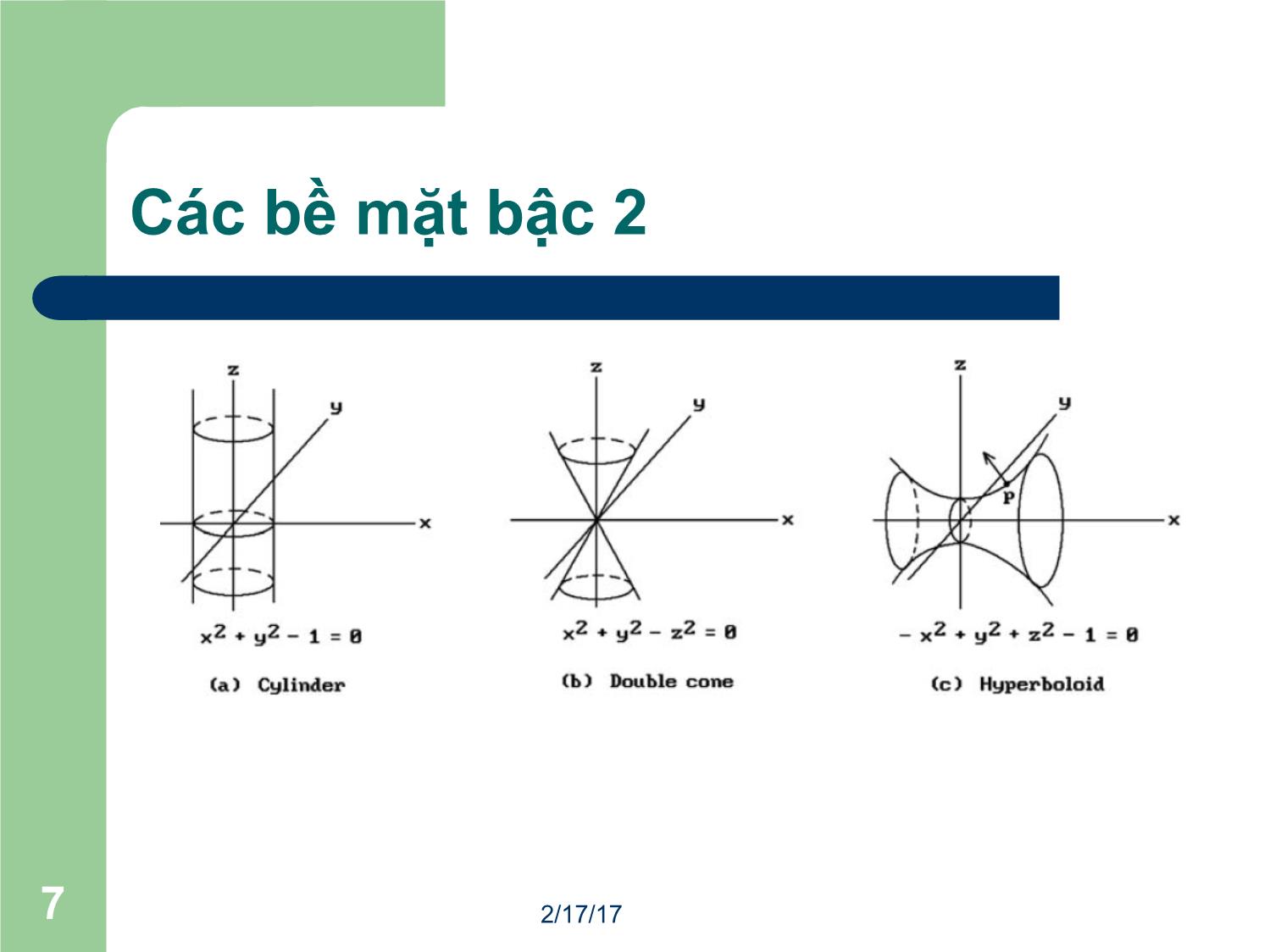
Trang 7
Bạn đang xem tài liệu "Bài giảng Đồ họa máy tính - Bài: Đường cong và bề mặt II - Mai Thị Châu", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Đồ họa máy tính - Bài: Đường cong và bề mặt II - Mai Thị Châu

2/17/171 Đồ họa máy tính Đường cong và bề mặt II 2/17/172 Bề mặt cong l Có thể mở rộng khái niệm đoạn cong cho các bề mặt cong. l Các bề mặt cong được xác định bởi công thức tham số của hai biến, s và t. l Nghĩa là, một bề mặt cong là một tập hợp các đường cong tham số l Xấp xỉ bằng một lưới đa giác. Khi vẽ, càng giảm nhỏ bước của s và t càng cho độ chính xác cao. 1010 ££££ tands s t Q(sc, t) Q(s, tc) 2/17/173 Bề mặt cong Bézier 2/17/174 Kiểm soát hình dạng của bề mặt l Điều khiển bởi một lưới 2D các điểm điều khiển. l Hàm bề mặt hai tham số có dạng: l Sử dụng các hàm cơ bản phù hợp cho các bề mặt Bézier và B-Spline. ),(),( )()(),( tsZandtsYforsimilarly qtfsftsX ijj ij iå= 2/17/175 Các bề mặt tròn xoay (a) bề mặt cầu, (b) bề mặt xuyến và (c) bề mặt parabol. 2/17/176 Các bề mặt bậc 2 0222 =+++++++++ jizhygxfyzexzdxyczbyax 2/17/177 Các bề mặt bậc 2
File đính kèm:
 bai_giang_do_hoa_may_tinh_bai_duong_cong_va_be_mat_ii_mai_th.pdf
bai_giang_do_hoa_may_tinh_bai_duong_cong_va_be_mat_ii_mai_th.pdf

