Bài giảng Đồ họa máy tính - Bài: Đường cong và bề mặt I - Mai Thị Châu
Tại sao lại dùng tham số?
l Các đường cong tham số rất linh hoạt.
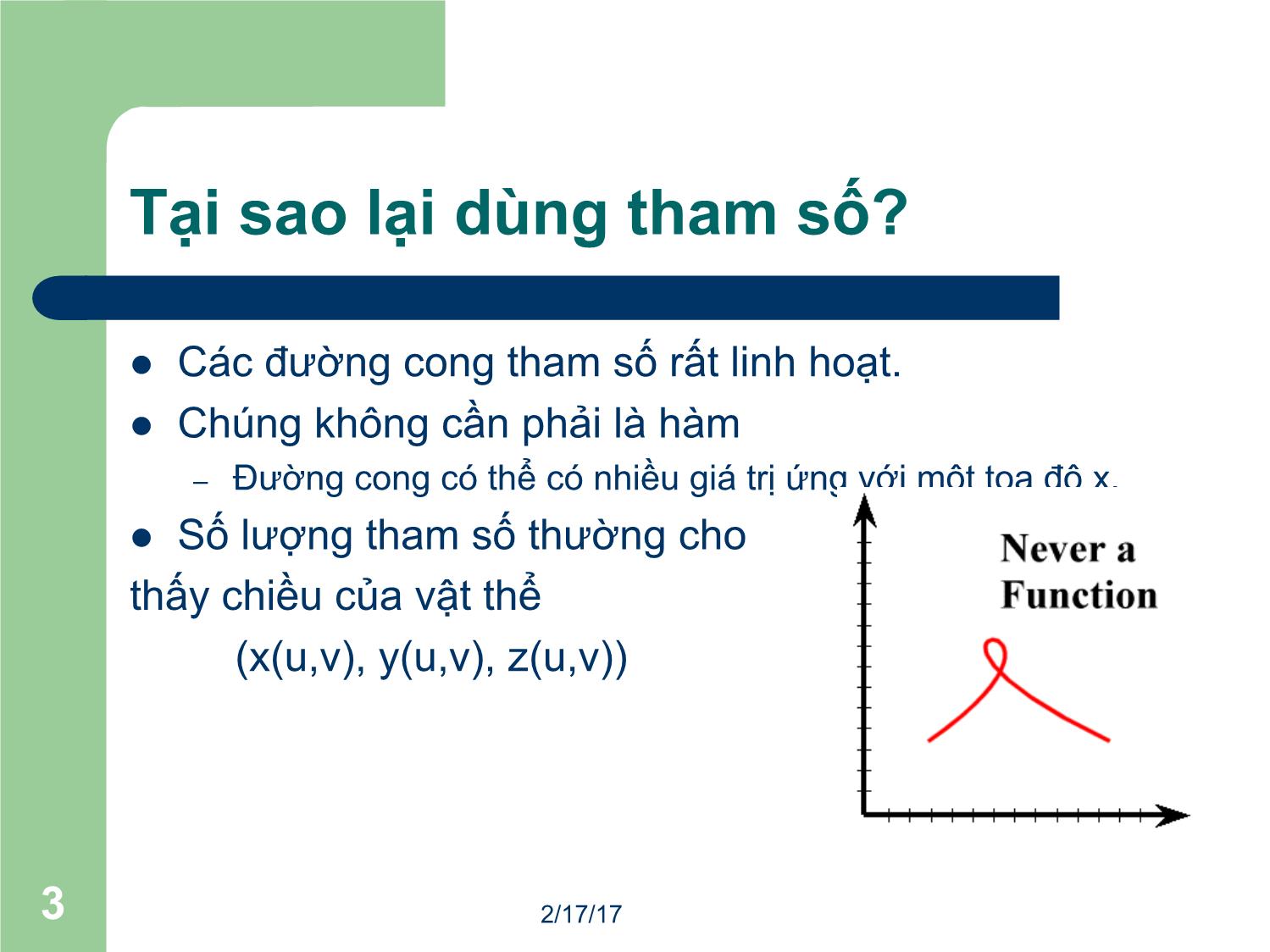
l Chúng không cần phải là hàm
– Đường cong có thể có nhiều giá trị ứng với một tọa độ x.
l Số lượng tham số thường cho
thấy chiều của vật thể
(x(u,v), y(u,v), z(u,v))

Trang 1

Trang 2
Trang 3
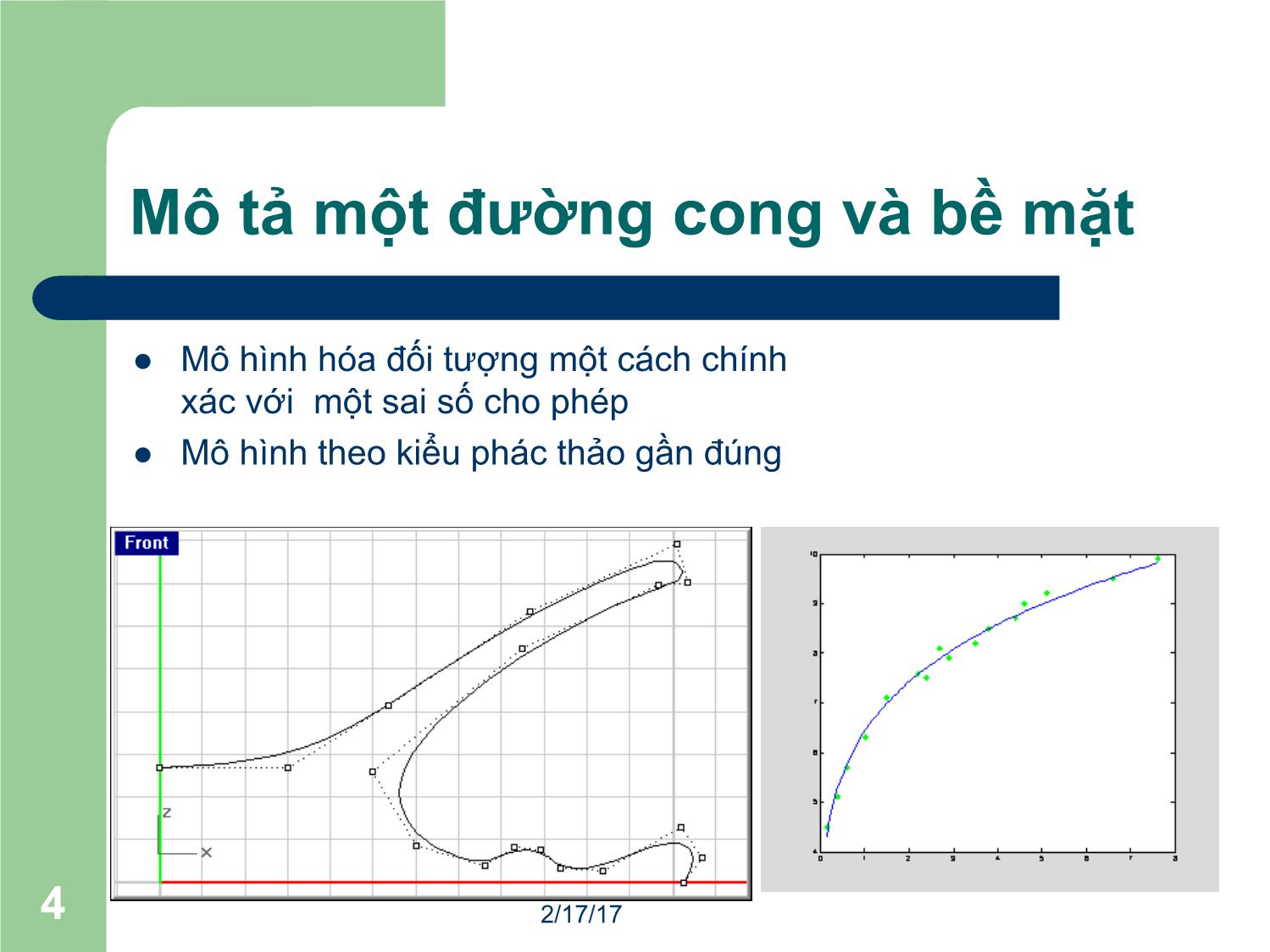
Trang 4

Trang 5

Trang 6

Trang 7

Trang 8

Trang 9
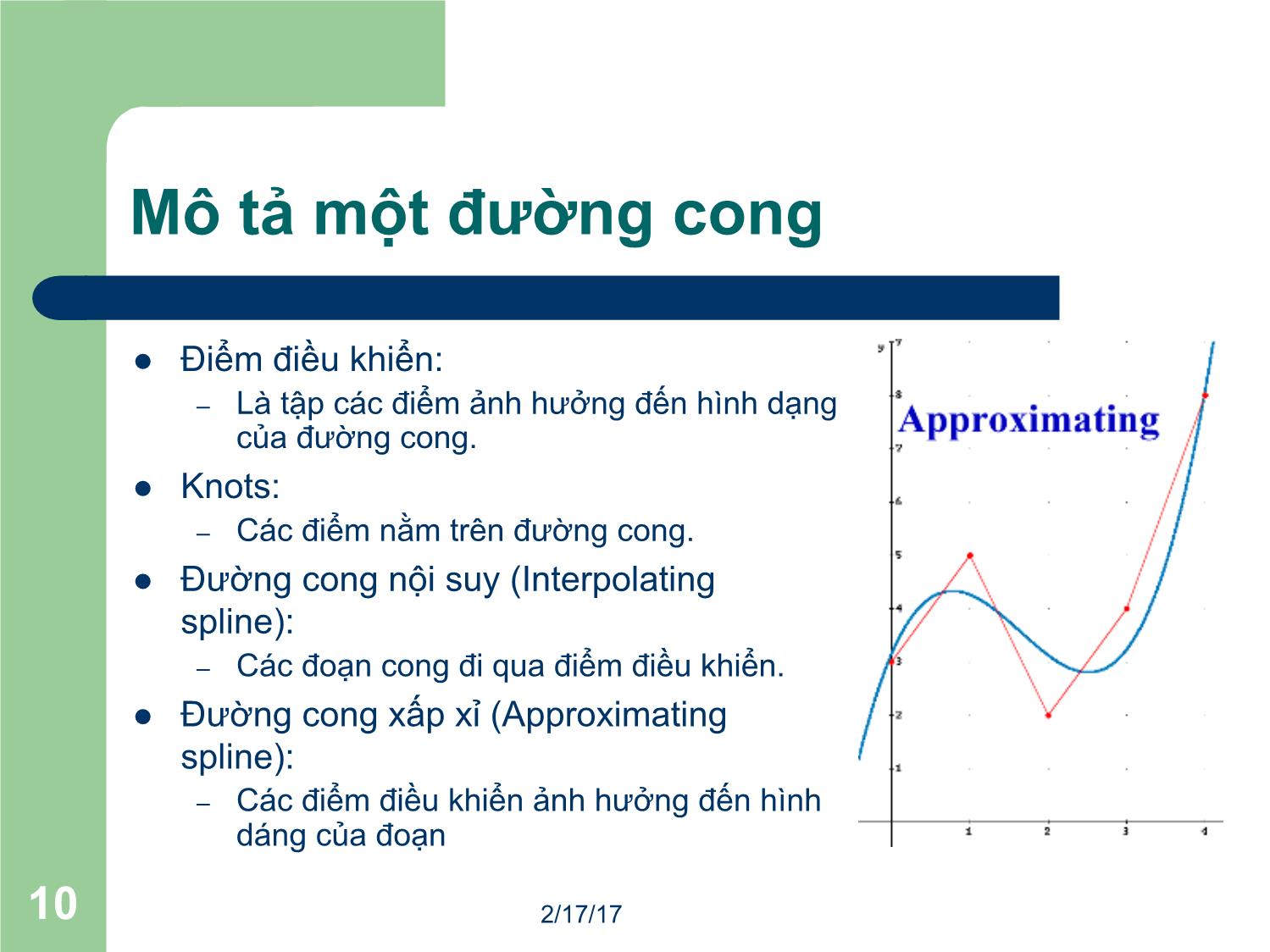
Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Đồ họa máy tính - Bài: Đường cong và bề mặt I - Mai Thị Châu", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Đồ họa máy tính - Bài: Đường cong và bề mặt I - Mai Thị Châu

2/17/171 Đồ họa máy tính Đường cong và bề mặt I 2/17/172 Biểu diễn các đối tượng cong • Bằng tham số • Qua ẩn của phương trình 2/17/173 Tại sao lại dùng tham số? l Các đường cong tham số rất linh hoạt. l Chúng không cần phải là hàm – Đường cong có thể có nhiều giá trị ứng với một tọa độ x. l Số lượng tham số thường cho thấy chiều của vật thể (x(u,v), y(u,v), z(u,v)) 2/17/174 Mô tả một đường cong và bề mặt l Mô hình hóa đối tượng một cách chính xác với một sai số cho phép l Mô hình theo kiểu phác thảo gần đúng 2/17/175 Bài toán xấp xỉ tổng quát l Hàm g là một xấp xỉ tốt với các tính chất sau: 1. Hàm g rất gần f theo một tính chất nào đó 2. Các hệ số ci là duy nhất 2/17/176 Bài toán xấp xỉ tổng quát l Cho một tập cố định các hàm φ1, φ2, , φk, tìm các hệ số ci sao cho: là một phép tính xấp xỉ đối với một hàm f(x) nào đó. Hàm φi thường được gọi là các hàm cơ sở (basic function) å = = k i ii xcxg 1 )()( j 2/17/177 Xấp xỉ bình phương tối thiểu l Hàm g(x, c1, c2, , ck) mà tối thiểu được gọi là xấp xỉ bình phương tối thiểu (least squares approximation) của hàm f(x) ( ) ( )å = -= s j kjjk cccxgxfcccE 1 2 2121 ),...,,;()(,...,, 2/17/178 Một số ràng buộc 1. Những ràng buộc nội suy: g(xj) = f(xj) với một số điểm xj cố định. 2. Kết hợp điều kiện (1) với những điều kiện về độ trơn, ví dụ như điều kiện về đạo hàm của g và f đồng nhất tại điểm xj. 3. Các ràng buộc về tính trực giao (f - g) • φi = 0 với mọi i. 4. Những ràng buộc về hình dạng trực quan, ví dụ như độ cong của đường cong và bề mặt. 2/17/179 Đường cong tham số với các hàm thành phần pi của p là các hàm giá trị thực thông thường với một biến thực. ))(),...,(),(()(,],[: 21 upupupupRbap m m =® 2/17/1710 Mô tả một đường cong l Điểm điều khiển: – Là tập các điểm ảnh hưởng đến hình dạng của đường cong. l Knots: – Các điểm nằm trên đường cong. l Đường cong nội suy (Interpolating spline): – Các đoạn cong đi qua điểm điều khiển. l Đường cong xấp xỉ (Approximating spline): – Các điểm điều khiển ảnh hưởng đến hình dáng của đoạn 2/17/1711 Phép nội suy Lagrange l Bài toán:cho các điểm (x0, y0), (x1, y1), , và (xn, yn), tìm một đa thức p(x), để p(xi) = yi với i = 0, 1, , n. l Đa thức Lagrange: ( ) ( ) ji jn ijjnnini xx xx xxxxLxL - - P== ¹= ,010,, ,...,,; ( ) ( )å = = n i nii xLyxp 0 , 2/17/1712 Phép nội suy Lagrange l Hạn chế - Bậc lớn nếu n lớn - Tạo vết gợn không mong muốn 2/17/1713 Các đoạn cong Chúng ta có thể biểu diễn một đường cong với độ dài bất kỳ bằng một chuỗi các đoạn cong nối với nhau. Chúng ta quan tâm đến các đoạn này nối với nhau như thế nào 2/17/1714 Đường cong tham số bậc 3 (Parametric Cubic Curves) l Để đảm bảo tính liên tục C2 các hàm của chúng ta phải có bậc ít nhất là 3. l Đường cong cubic có 4 bậc tự do và thay đổi 4 thứ. l Sử dụng thức: x(t) có bậc n là một hàm của t. - y(t) và z(t) cũng tương tự và được xử lý độc lập. l Có nghĩa là: i n i i xatx å = = 0 )( 2/17/1715 Đường cong Hermite l 4 bậc tự do, 2 để điều khiển tính liên tục C0 và C1 tại mỗi đầu. l Sử dụng đa thức để biểu diễn đường cong. l Xác định: x = X(t) theo các giá trị x0, x0/, x1, x1/ Bây giờ: X(t) = a3t3 + a2t2 + a1t + a0 và X/(t) = 3a3t2 + 2a2t + a1 2/17/1716 Tìm các hệ số Hermite Thay t vào hai đầu: x0 = X(0) = a0 x0/ = X/(0) = a1 x1 = X(1) = a3 + a2 + a1 + a0 x1/ = X/(1) = 3a3 + 2a2+ a1 Và lời giải là: a0 = x0 a1 = x0/ a2 = -3x0 – 2x0/ + 3x1 – x1/ a3 = 2x0 + x0/ - 2x1 + x1/ 2/17/1717 Ma trận Hermite: MH Đa thức kết quả có thể được biểu diễn qua dạng ma trận: X(t) = tTMHq ( q là véc-tơ điều khiển) [ ] ú ú ú ú û ù ê ê ê ê ë é ú ú ú ú û ù ê ê ê ê ë é --- - = / 1 1 / 0 0 23 0001 0010 1323 1212 1)( x x x x ttttX Bây giờ chúng ta có thể định nghĩa đa giác tham số cho các tọa độ một cách độc lập X(t), Y(t) và Z(t) 2/17/1718 Các hàm Hermite cơ bản )1()( )1()( )23()( )12()1()( 2 4 2 3 2 2 2 1 -= -= -= +-= xxxF xxxF xxxF xxxF 2/17/1719 Các hàm Hermite cơ bản x0 x1 x0/ x1/ Đồ thị cho thấy hình dạng của bốn hàm cơ bản (hay còn gọi là blending functions). Chúng được gán nhãn với thành phần trọng số của nó. 2/17/1720 Bài toán nội suy ghép đoạn Hermite Cho các bộ ba (x0, y0, m0), (x1, y1, m1), ..., và (xn, yn, mn), tìm các đa thức bậc ba pi(x), i = 0, 1, ..., n-1, để pi(xi) = yi, pi’(xi) = mi, pi(xi+1) = yi+1, và pi’(xi+1) = mi+1
File đính kèm:
 bai_giang_do_hoa_may_tinh_bai_duong_cong_va_be_mat_i_mai_thi.pdf
bai_giang_do_hoa_may_tinh_bai_duong_cong_va_be_mat_i_mai_thi.pdf

