Bài giảng Đồ họa hiện thực ảo - Bài 7: Đường cong trong không gian 3D curve - Lê Tấn Hưng

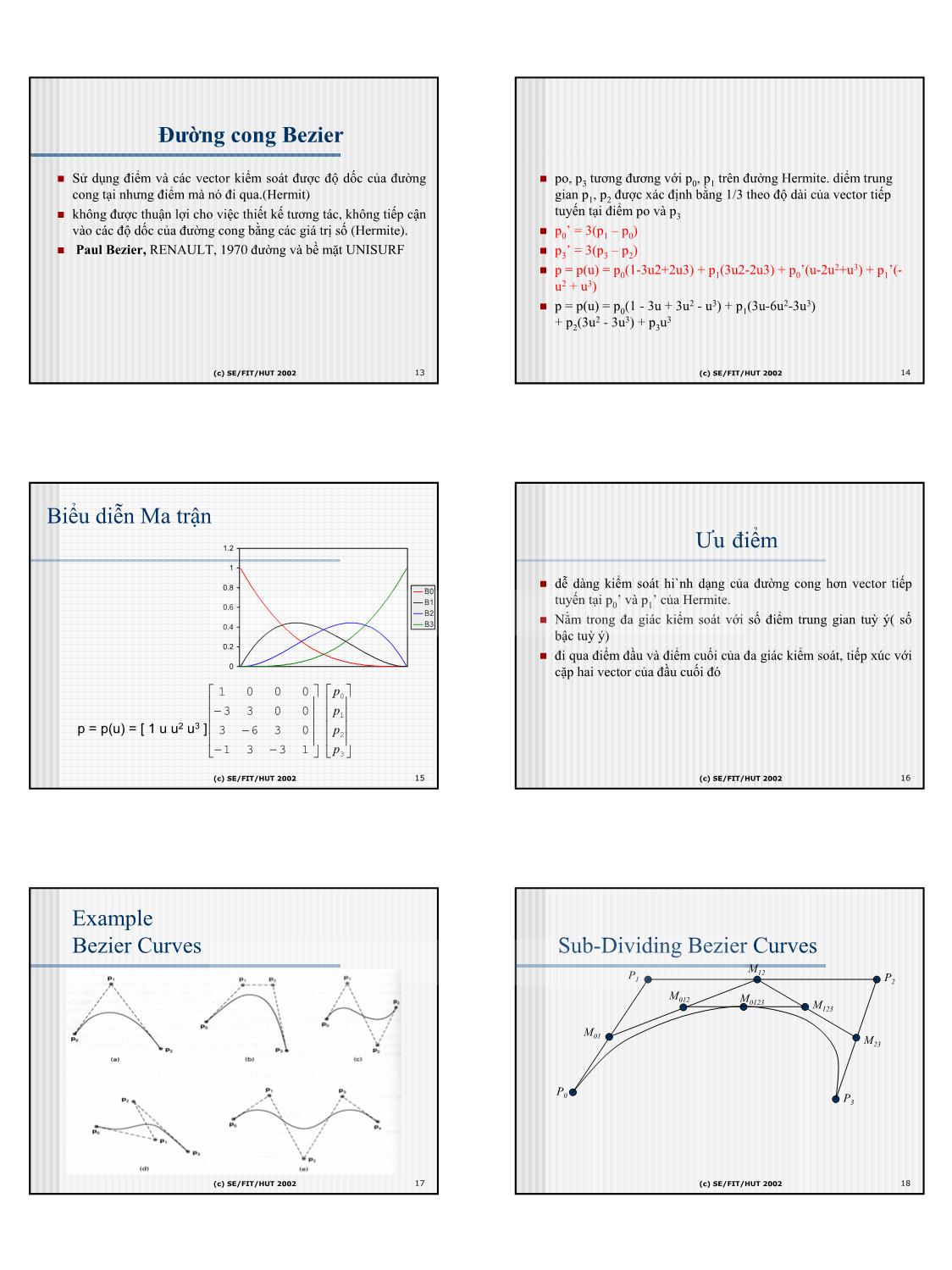
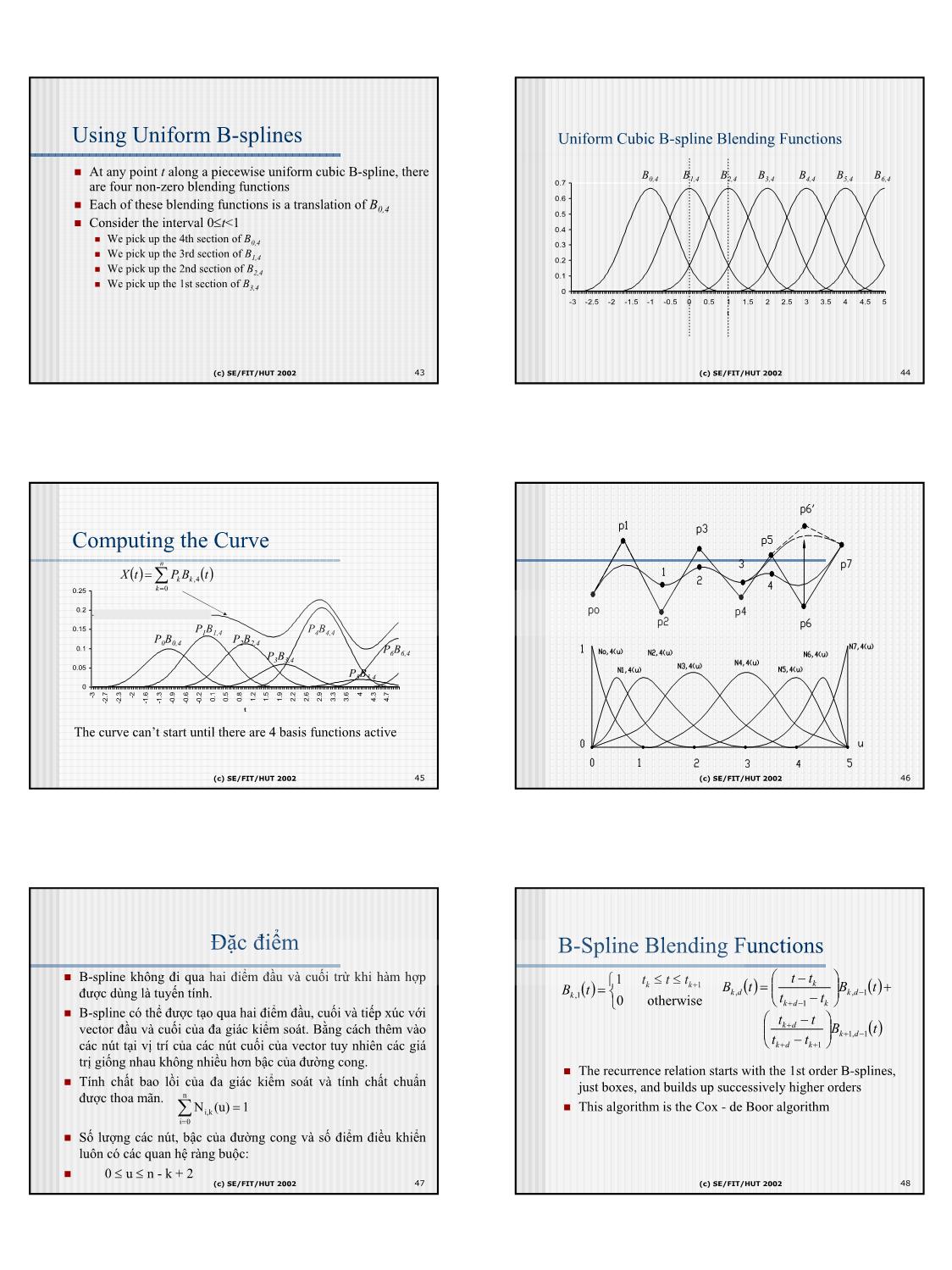
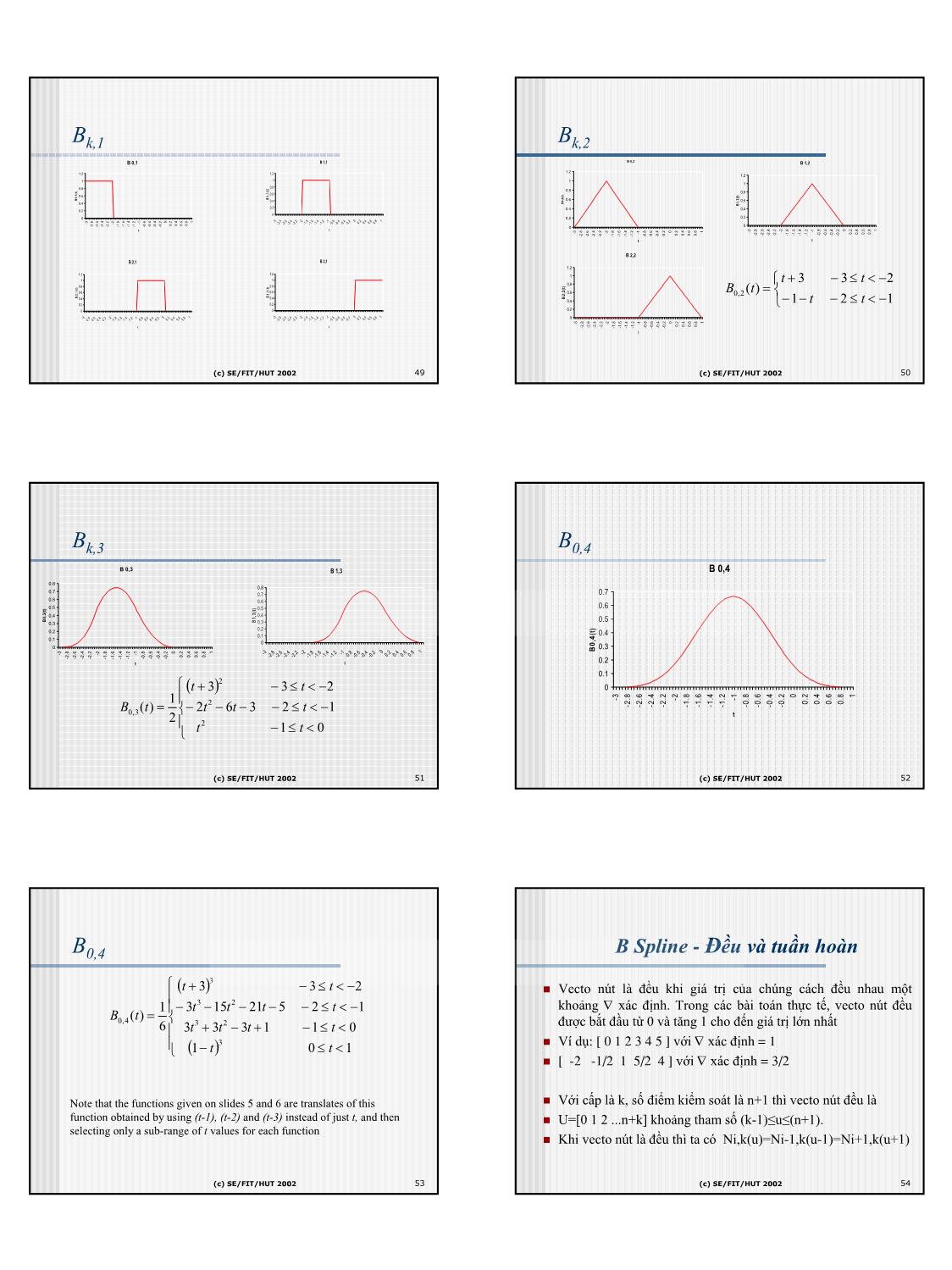
sing a repeated-lirping procedure.
  But this time, we can use any number of control points.
 (c) SE/FIT/HUT 2002 35 (c) SE/FIT/HUT 2002 36
 6
CNTT-DHBK Hanoi
hunglt@it-hut.edu.vn
 B-Splines:
 B-Splines
 The Idea [2/2]
  We form an order-2 B-Spline by lirping between the order-1 blending functions.
  As discussed, we get functions that start at 0, ramp up to 1 and back down, then stay at Types of B-Splines Approximation Curves Used
 zero. Each function is 0 most of the time.
  So each blending function is defined in pieces. Each piece is a polynomial of degree 1 B-Spline approximations can be classified based on the 
 (graph is a line). spacing of the knot vector and the use of weights. 
  So an order-2 B-spline is just the control polygon.
  Again, any number of control points may be used. 1. Uniform/Periodic B-splines : The spacing is
  We form an order-3 B-Spline by lirping between the order-2 blending functions. unform and the knots (control points) are equispaced e.g. 
 [0,1,2,3,4,5] These have satisfactory smoothness but lack 
  Now blending functions are smooth. They start at 0, curve up to 1 then back down. 
 Again, each function is 0 most of the time. local control and the starting and ending poits are ill 
 defined as above. 
  Again, each blending function is defined in pieces. Each piece is a polynomial of 
 degree 2. 2. Non-periodic: The knots are repeated at the ends m 
 times and the interior is equispaced. e.g. [0 0 0 1 2 3 3 3 
  We continue this repeated-lirping procedure to define B-splines of higher order.
 ] These can be used to force the control point to start 
  See the blue book for details and graphs. and finish at a control point. 
 3. Non-uniform B-Splines : The spacing is non-
 uniform and or repeated knots e.g. [0 1124566 
 ] These can be used to obtain local control
 (c) SE/FIT/HUT 2002 37 (c) SE/FIT/HUT 2002 38
 Ví dụ: Uniform Cubic B-spline on 
 [0,1] Basis Functions on [0,1]
  Four control points are required to define the curve for 0≤t<1 (t is the  Does the curve interpolate its endpoints?
 parameter)
  Does it lie inside its convex hull?
  Not surprising for a cubic curve with 4 degrees of freedom 0.7 B1,4
 B2,4
  The equation looks just like a Bezier curve, but with different basis functions 0.6
  Also called blending functions - they describe how to blend the control points to 
 0.5
 make the curve P (t ) P 1 t t 2 t 3
 = 0 ()1−3 + 3 −
 0.4 6
 0.3
 P 1 t 2 t 3
 + 1 ()4 − 6 + 3
 3 0.2 B0,4 B3,4
 61
 P (t ) = Pi Bi , (t )
 ∑ 4 0.1
 i =
 0 + P 1 ()+ t + t 2 − t 3
 0 2 1 3 3 3
 = P 1 ()− t + t 2 −t 3 + P 1 ()− t 2 + t 3 + P 1 ()+ t + t 2 − t 3 + P 1 ()t 3 6
 0 1 3 3 4 6 3 2 1 3 3 3 3 0 .5 1
 6 61 6 6 0.1 0.2 0.3 0.4 0 0.6 0.7 0.8 0.9
 t P 1 t 3
 + 3 ()
 6
 (c) SE/FIT/HUT 2002 39 (c) SE/FIT/HUT 2002 40
 Uniform Cubic B-spline on [0,1) Uniform - B-spline
 n
  The blending functions sum to one, and are positive everywhere 1 u ∈[u ,u ]
 P(u) = N (u).P i i+1
  The curve lies inside its convex hull ∑ i,k i Ni,1(u) = 
 i=0 0 others
  The curve does not interpolate its endpoints
  Requires hacks or non-uniform B-splines (u −U ) (U − u)
 N (u) = i+1−k N (u) + i+1 N (u)
  There is also a matrix form for the curve: i,k i−1,k −1 i,k −1
 U i −U i+1−k (U i+1 −U i+2−k )
  Ni,k(u) đa thức B-Spline cơ bản
 3
  −1 3 −3 1t   Vớin+ 1 sô điểmkiểmsoát
   
 − t 2
 P (t ) = 1 P P P P  3 6 0 4   Pi điểm kiểm soát thứ i
 []0 1 2 3
 6 − 3 3 3 1 t 
     k bậc của đường cong 1<k<n+2
  1 0 0 0 1  Ui vector nút của đường cong U=[U1,U2...Un+k+1]
 (c) SE/FIT/HUT 2002 41 (c) SE/FIT/HUT 2002 42
 7
CNTT-DHBK Hanoi
hunglt@it-hut.edu.vn
 Using Uniform B-splines Uniform Cubic B-spline Blending Functions
  At any point t along a piecewise uniform cubic B-spline, there 
 B0,4 B1,4 B2,4 B3,4 B4,4 B5,4 B6,4
 are four non-zero blending functions 0.7
 0.6
  Each of these blending functions is a translation of B0,4
 0.5
  Consider the interval 0≤t<1
 0.4
  We pick up the 4th section of B
 0,4 0.3
  We pick up the 3rd section of B
 1,4 0.2
  We pick up the 2nd section of B
 2,4 0.1
  We pick up the 1st section of B3,4
 0
 -3 -2.5 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
 t
 (c) SE/FIT/HUT 2002 43 (c) SE/FIT/HUT 2002 44
 Computing the Curve
 n
 X ()t = ∑ Pk Bk,4 ()t
 0.25 k =0
 0.2
 0.15
 P1B1,4 P4B4,4
 P0B0,4 P2B2,4
 0.1
 P6B6,4
 P3B3,4
 0.05
 P5B5,4
 0
 4
 -3 -2
 0.1 0.5 0.8 1.2 1.5 1.9 2.2 2.6 2.9 3.3 3.6 4.3 4.7
 -2.7 -2.3 -1.6 -1.3 -0.9 -0.6 -0.2
 t
 The curve can’t start until there are 4 basis functions active
 (c) SE/FIT/HUT 2002 45 (c) SE/FIT/HUT 2002 46
 Đặc điểm B-Spline Blending Functions
  B-spline không đi qua hai điểm đầu và cuối trừ khi hàm hợp  
 1 tk ≤ t ≤ tk+1 t − tk
 B ()t = Bk ,d ()t =  Bk,d −1()t +
 được dùng là tuyến tính. k ,1   t − t 
 0 otherwise  k +d −1 k 
  B-spline có thể được tạo qua hai điểm đầu, cuối và tiếp xúc với  t − t 
  k+d 
 vector đầu và cuối của đa giác kiểm soát. Bằng cách thêm vào  Bk+1,d −1()t
 các nút tại vị trí của các nút cuối của vector tuy nhiên các giá  tk +d − tk+1 
 trị giống nhau không nhiều hơn bậc của đường cong.
  The recurrence relation starts with the 1st order B-splines, 
  Tính chất bao lồi của đa giác kiểm soát và tính chất chuẩn just boxes, and builds up successively higher orders
 được thoa mãn. n
 
 ∑ Ni,k (u) = 1 This algorithm is the Cox - de Boor algorithm
 i=0
  Số lượng các nút, bậc của đường cong và số điểm điều khiển 
 luôn có các quan hệ ràng buộc: 
  0 ≤ u ≤ n - k + 2
 (c) SE/FIT/HUT 2002 47 (c) SE/FIT/HUT 2002 48
 8
CNTT-DHBK Hanoi
hunglt@it-hut.edu.vn
 Bk,1 Bk,2
 B 0,1 B 1,1 B 0,2 B 1,2
 1.2
 1.2 1.2 1.2
 1 1 1
 1
 0.8
 0.8 )
 t
 ( 0.8
 0.6 0.8
 0.6
 B1,1
 B0,1(t) 0.4 0.6 0.6
 0.4 B0,2(t)
 B1,2(t)
 0.2 0.4
 0.2 0.4
 0
 0 0.2 0.2
 2 0 1
 0 1 -3 8 6 4 2 - 8 .6 4 2 -1 .8 6 4 2 .4
 -3 -2 -1 -2. -2. -2. -2. -1. -1 -1. -1. -0 -0. -0. -0. 0.2 0 0.6 0.8
 0.2 0.4 0.6 0.8
 -2.8 -2.6 -2.4 -2.2 -1.8 -1.6 -1.4 -1.2 -0.8 -0.6 -0.4 -0.2 0 0
 t t 0 1
 -3 -2 -1
 0 1
 -3 -2 -1
 0.2 0.4 0.6 0.8
 0.2 0.4 0.6 0.8
 -2.8 -2.6 -2.4 -2.2 -1.8 -1.6 -1.4 -1.2 -0.8 -0.6 -0.4 -0.2
 -2.8 -2.6 -2.4 -2.2 -1.8 -1.6 -1.4 -1.2 -0.8 -0.6 -0.4 -0.2
 t t
 B 2,2
 B 2,1 B 3,1
 1.2
 1.2 1.2 1
 1 1
 0.8 t + 3 − 3 ≤ t < −2
 ) 0.8
 ) 0.8
 t
 t
 (
 (
 1
 0.6 , 0.6 0.6 B0,2 (t) =
 B3 
 B2,1
 0.4 0.4 B2,2(t)
 0.4 −1− t − 2 ≤ t < −1
 0.2 0.2 
 0 0 0.2
 3 2 0 1
 -3 8 .6 .4 2 -2 8 6 .4 .2 -1 8 6 4 2 0 6 8 1 - 8 .6 .4 2 - .8 .6 4 2 -1 8 6 .4 .2 2 4 .6 8 0
 -2. -2 -2 -2. -1. -1. -1 -1 -0. -0. -0. -0. 0.2 0.4 0. 0. -2. -2 -2 -2. -1 -1 -1. -1. -0. -0. -0 -0 0. 0. 0 0.
 0 1
 -3 -2 -1
 0.2 0.4 0.6 0.8
 t t -2.8 -2.6 -2.4 -2.2 -1.8 -1.6 -1.4 -1.2 -0.8 -0.6 -0.4 -0.2
 t
 (c) SE/FIT/HUT 2002 49 (c) SE/FIT/HUT 2002 50
 Bk,3 B0,4
 B 0,3 B 1,3 B 0,4
 0.8
 0.8
 0.7
 0.7 0.7
 0.6 0.6
 0.5 0.5 0.6
 0.4 0.4
 B0,3(t)
 B1,3(t) 0.5
 0.3 0.3
 0.2 0.2
 0.1 0.4
 0.1
 0
 0 0.3
 B0,4(t)
 0 1 6 8 6 8 2 0 1
 -3 -2 -1 -3 .8 .2 -2 .4 .2 -1 .4 .2 .4
 0.2 0.4 0.6 0.8 -2 -2. -2.4 -2 -1. -1. -1 -1 -0. -0.6 -0 -0. 0 0 0.6 0.8
 -2.8 -2.6 -2.4 -2.2 -1.8 -1.6 -1.4 -1.2 -0.8 -0.6 -0.4 -0.2
 t t 0.2
 0.1
 2
 ()t + 3 − 3 ≤ t < −2 0
 0 1
 -3 -2 -1
 1  2 0.2 0.4 0.6 0.8
 B (t) = − 2t − 6t − 3 − 2 ≤ t < −1 -2.8 -2.6 -2.4 -2.2 -1.8 -1.6 -1.4 -1.2 -0.8 -0.6 -0.4 -0.2
 0,3  t
 2  2
  t −1 ≤ t < 0
 (c) SE/FIT/HUT 2002 51 (c) SE/FIT/HUT 2002 52
 B0,4 B Spline - Đềuvàtuần hoàn
 3
  ()t + 3 − 3 ≤ t < −2  Vecto nút là đều khi giá trị của chúng cách đều nhau một 
 
 1 − 3t3 −15t 2 − 21t − 5 − 2 ≤ t < −1 khoảng ∇ xác định. Trong các bài toán thực tế, vecto nút đều 
 B (t) =
 0,4  3 2 được bắt đầu từ 0 và tăng 1 cho đến giá trị lớn nhất 
 6  3t + 3t − 3t +1 −1 ≤ t < 0
 3  Ví dụ: [ 0 1 2 3 4 5 ] với ∇ xác định = 1
  ()1− t 0 ≤ t < 1
  [ -2 -1/2 1 5/2 4 ] với ∇ xác định = 3/2
 Note that the functions given on slides 5 and 6 are translates of this  Với cấp là k, số điểm kiểm soát là n+1 thì vecto nút đều là
 function obtained by using (t-1), (t-2) and (t-3) instead of just t, and then  U=[0 1 2 ...n+k] khoảng tham số (k-1)≤u≤(n+1).
 selecting only a sub-range of t values for each function
  Khi vecto nút là đều thì ta có Ni,k(u)=Ni-1,k(u-1)=Ni+1,k(u+1)
 (c) SE/FIT/HUT 2002 53 (c) SE/FIT/HUT 2002 54
 9
CNTT-DHBK Hanoi
hunglt@it-hut.edu.vn
 Không tuần hoàn B-Splines:
 Open – Non Uniform Properties
  Một vector không tuần hoàn hoặc mở là Cấp số lượng nút (m Vector nút  The most used B-splines are:
 vector nút có giá trị nút tại các điểm đầu k = n + k) không tuần  Order 3 (“quadratic B-splines”).
 • Smooth.
 cuối lặp lại với số lượng các giá trị lặp hoàn
  Order 4 (“cubic B-splines”).
 lại này bằng chính cấp k của đường cong 2 6 [0 0 1 2 3 3] • Smoother, but control is a little less local.
 và các giá trị nút trong mỗi điểm lặp này  B-splines have the following properties.
 là bằng nhau  An order-k B-spline has blending functions that are defined in pieces, using 
 3 7 [0 0 0 1 2 2 2] polynomials of degree k–1.
  Nếu một trong hai điều kiện này hoặc cả hai 
 • This is true for any number of control points. We can choose the number of control points and 
 điều kiện không được thoả mãn thì vecto nút the polynomial degree separately. ☺
 là không đều. 4 8 [0 0 0 0 1 1 1 1]  B-splines are affine invariant (of course).
  Cách tính Ui  They have the convex-hull property. ☺
 Ui = 0 1=<i<=k  They have local control. ☺
  A B-spline (of order 3 or more) does not interpolate any of its control points.  But we 
 Ui = i-k k+1<i<=n+1 can deal with this 
 Ui = n-k+2 n+1<i<=n+k+1
 (c) SE/FIT/HUT 2002 55 (c) SE/FIT/HUT 2002 56
 Kếtluận Rational Curves
  B-spline là một dòng của Bezier  Each point is the ratio of two curves
  Thực tế khi ta chọn bậc k cho tập hợp k điểm thì thi B-spline chuyển thành  Just like homogeneous coordinates:
 Bezier  x(t) y(t) z(t) 
 [x(t), y(t), z(t), w(t)] →  , , 
  Khi bậc của đa thức giảm sựảnh hưởng cục bộ của mỗi điểm nút càng rõ w(t) w(t) w(t)
 ràng hơn.  NURBS: x(t), y(t), z(t) and w(t) are non-uniform B-splines
  Khi tồn tại anh hưởng cục bộ càng lớn và đường cong phai đi qua điểm đó.  Advantages:
  Chúng ta có thể thay đổi hình dạng đường cong B-spline bằng cách:  Perspective invariant, so can be evaluating in screen space
  Thay đổi kiểu vecto nút : đều tuần hoàn, mở, không đều  Can perfectly represent conic sections: circles, ellipses, etc
 • Piecewise cubic curves cannot do this
  Thay đổi cấp k của đường cong
  Thay đổi số đỉnh và vị trí các đỉnh đa giác kiểm soát
  Sử dụng các điểm kiểm soát trùng nhau
 (c) SE/FIT/HUT 2002 57 (c) SE/FIT/HUT 2002 58
 Rational Spline - NURBS OpenGL and NURBS
  A Rational Spline is like a B-Spline L  NURBS: Non-uniform Rational B-splines
 but the designer can add weightings  The curved surface of choice in CAD packages
 to the blending functions to modify (t ) =
 P ∑P k R k (t )  Support routines are part of the GLu utility library
 the curve. k =0
  Allows you to specify how they are rendered:
  Can use points constantly spaced in parametric space
 (t)  Can use various error tolerances - the good way!
  The blending functions produce a k k ,m
 (t) = w N  Allows you to get back the lines that would be drawn
 ratio of the polynomials used. Rk L
 (t)  Allows you to specify trim curves
 ∑wk N k ,m
 k =0  Only for surfaces
  Cut out parts of the surface - in parametric space
 (c) SE/FIT/HUT 2002 59 (c) SE/FIT/HUT 2002 60
 10
CNTT-DHBK Hanoi
hunglt@it-hut.edu.vn
 Other Splines:
 Non-uniform Rational B-Splines(NURBS)
 NURBS, etc.
 The last 3 types are good for representing free form curves but also introduce  There are any number of other types of splines.
 unnecessary approximations in the representation of conic sections. NURBS build on  Often we want a very general type of curve that will do whatever we want.
 non-uniform B-Splines and introduce a weight function to obtain an approximation  One such type of curve that has been very successful is the NURBS.
 that retains all the advantages of the non-uniform B-Splines and is also capable of  NURBS = Non-Uniform Rational B-Spline.
 exact representation of conic sections (circles, parabolas etc.).The general form is  A NURBS is defined using rational functions.
 given below: • A rational function is a polynomial divided by a polynomial.
  Control points can be given weights, so some are more important than others.
  NURBS curves (and surfaces) are built into GLU, but can be rather complex to use.
  One important issue when defining curves and surfaces:
  In advanced rendering the technique of ray tracing is often used.
  In ray tracing, we determine the color of a pixel by tracing a ray of light backward from 
 the viewer’s eye, through the pixel, and we see where the ray came from.
 The curve is described as rational since it is expressed as the ratio of two 
  In order to do ray tracing efficiently, we must be able to test quickly whether a 
 polynomials. wi defines a weight function. If wi is set to 1 we get back the non- particular ray hits a particular object and, if so, where.
 uniform B-Spline. Other values of the wi can be used to produce curves for straight  Types of surfaces in which this test can be done quickly will be more useful in 3-D 
 line, parabola, ellipse and hyperbola. graphics.
 (c) SE/FIT/HUT 2002 61 (c) SE/FIT/HUT 2002 62
 Tính chất cả đường cong đa thức How to Choose a Spline
  Tham biến – parametric sử dụng tham biến ngoài để biểu diễn cho các  Hermite curves are good for single segments where you know the 
 tham biến trong parametric derivative or want easy control of it
  Độ mượt - smooth. Với đường cong Hermite and Bézier tính liên tục  Bezier curves are good for single segments or patches where a user 
 continuity của đường cong hay đạo hàm bậc 1-first derivative tại các điểm controls the points
 kiểm soát-control point. Với B-splines tính liên tục trên đạo hàm bậc 2 
 second derivative hay độ cong được đảm bảo curvature.  B-splines are good for large continuous curves and surfaces
  Độ biến đổi -"variation diminishing." đường cong ít bị khuếch đại sai  NURBS are the most general, and are good when that generality is useful, 
 số bởi các điểm kiểm soát hay tính nhấp nhô của đường cong hạn chế - or when conic sections must be accurately represented (CAD)
 oscillate. 
  Ví dụ Bézier curve, for instance, lies within the convex hull (polygon 
 envelope) of the set of control points. 
  Điêm kiểm soát cục bộ-local control. đường cong bịảnh hưởng mạnh 
 nhất với chính các điểm kiểm soát gần chúng nhất.
 (c) SE/FIT/HUT 2002 63 (c) SE/FIT/HUT 2002 64
 11