Bài giảng Đồ họa hiện thực ảo - Bài 5: Nguyên lý về 3D và Phép chiếu-Projection - Lê Tấn Hưng
Nguyên lý về 3D
Ðồ họa 3 chiều - 3D computer graphics bao gồm việc bổ
xung kích thước về chiều sâu của đối tượng, cho phép ta biểu
diễn chúng trong thế giới thực một cách chính xác và sinh
động hơn.
Tuy nhiên các thiết bị truy xuất hiện tại đều là 2 chiều, Do
vậy việc biểu diễn được thực thi thông qua phép tô chát –
render để gây ảo giác illusion về độ sâu
3D Graphics là việc chyển thế giới tự nhiên dưới dạng các mô
hình biểu diễn trên các thiết bị hiển thị thông qua kỹ thuật tô
chát (rendering).

Trang 1

Trang 2

Trang 3

Trang 4

Trang 5
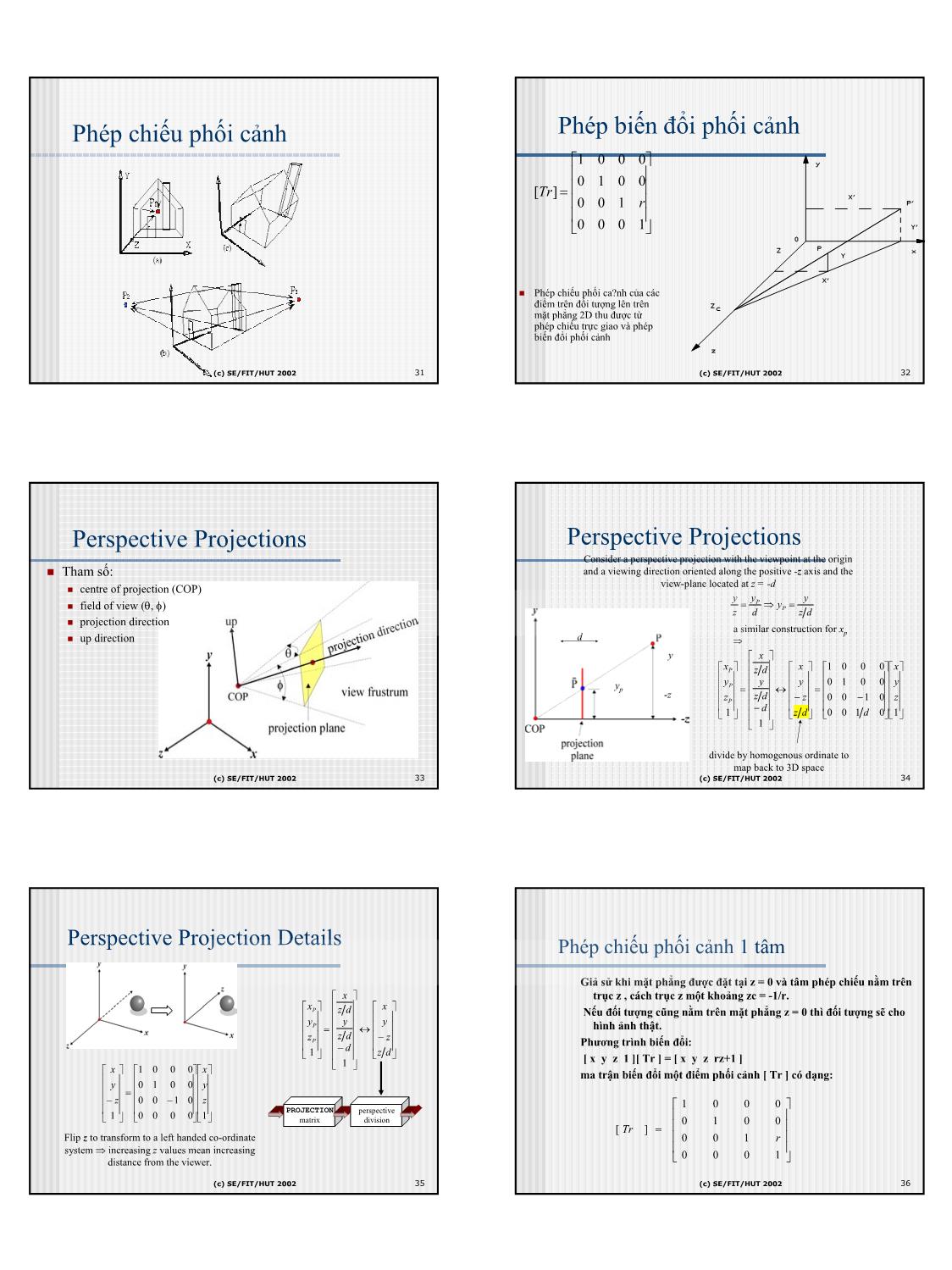
Trang 6

Trang 7

Trang 8
Bạn đang xem tài liệu "Bài giảng Đồ họa hiện thực ảo - Bài 5: Nguyên lý về 3D và Phép chiếu-Projection - Lê Tấn Hưng", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Đồ họa hiện thực ảo - Bài 5: Nguyên lý về 3D và Phép chiếu-Projection - Lê Tấn Hưng

Khoa CNTT – DHBK Hanoi hunglt@it-hut.edu.vn 8682595 Bài 5 Nguyên lý về 3D và Nguyên lý về 3D Phép chiếu-Projection Ðồ họa3 chiều - 3D computer graphics bao gồmviệcbổ xungkíchthướcvề chiềusâucủa đốitượng, cho phép ta biểu diễn chúng trong thế giớithựcmột cách chính xác và sinh động hơn. Tuy nhiên các thiếtbị truy xuấthiệntại đềulà2 chiều, Do Lê Tấn Hùng vậyviệcbiểudiễn đượcthực thi thông qua phép tô chát – 0913030731 render để gây ảo giác illusion vềđộsâu hunglt@it-hut.edu.vn 3D Graphics là việcchyểnthế giớitự nhiên dướidạng các mô hình biểudiễn trên các thiếtbị hiểnthị thông qua kỹ thuậttô chát (rendering). (c) SE/FIT/HUT 2002 1 (c) SE/FIT/HUT 2002 2 Ðặc điểmcủakỹ thuật đồ hoạ 3D Các phương pháp hiểnthị 3D Có các đốitượng phứctapjhơn các đốitượng trong Vớicácthiếtbị hiểnthị 2D: không gian 2D 3D viewing positions Bao bởi các mặtphẳng hay các bề mặt Kỹ thuậtchiếu - projection: orthographic/perspective Có các thành phần trong và ngoài Kỹ thuật đánh dấu độ sâu - depth cueing Các phép biến đổihìnhhọcphứctạp Nét khuất - visible line/surface identification Các phép biến đổihệ toạđộphứctạphơn Tô chát bề mặt-surface rendering Cắt lát - exploded/cutaway scenes, cross-sections Thường xuyên phảibổ xung thêm phép chiếutừ không gian 3D vào không gian 2D Thiếtbị hiểnthị 3D: Kính stereo - Stereoscopic displays* Luôn phảixácđịnh các bề mặthiểnthị Màn hình 3D - Holograms (c) SE/FIT/HUT 2002 3 (c) SE/FIT/HUT 2002 4 Perspective and Exploded/cutaway scenes Depth of Field 3D GRAPHICS PIPELINE WORLD SCENE/OBJECT Shadows as depth cues Modelling coordinates: - world coordinate system, 3D MODELLING - object coordinate system VIEWING 3D CLIPPING Camera coordinates PROJECTION Screen/Window coordinates RASTERIZATION Device coordinates Different views of a 3D model 2D PIXELMAP DISPLAY (c) SE/FIT/HUT 2002 5 (c) SE/FIT/HUT 2002 6 1 Khoa CNTT – DHBK Hanoi hunglt@it-hut.edu.vn 8682595 3D - Modelling Clipping 3D x2 + y2 + z2 = r2 view frustrum Polygonal Implicit 3D Modelling x = sin4θ y = cos2θ outside view so must be clipped Parametric Particles (c) SE/FIT/HUT 2002 7 (c) SE/FIT/HUT 2002 8 Viewing and Projection Rasterization 3d models camera setup viewport (c) SE/FIT/HUT 2002 9 (c) SE/FIT/HUT 2002 10 Phép chiếu Các bướcxâydựng hình chiếu täa ®é thùc täa ®é theo vïng täa ®é thiÕt khung nh×n 3D c¾t bÞ Định nghĩavề phép chiếu PhÐp biÕn ®æi vµo C¾t theo view PhÐp chiÕu trªn cæng nh×n cña volum mÆt ph¼ng chiÕu täa ®é thiÕt bÞ Định nghĩavề hình chiếu 1. đốitượng trong không gian 3Dvớitọa độ thực đượccắttheomột không gian Ảnh của đốitượng trên mặtphẳng chiếu được hình thành từ xác định gọilàviewvolume. phép chiếubởi các đường thẳng gọi là tia chiếu projector ( ) 2. view volume đượcchiếulênmặtphẳng chiếu. Diện tích choán bởiviewvolume xuất phát từ một điểmgọilàtâmchiếu (center of projection) trên mặtphẳng chiếu đósẽ cho chúng ta khung nhìn. đi qua các điểmcủa đốitượng giao vớimặtchiếu (projection 3. là việcánhxạ khung nhìn vào trong mộtcổng nhìn bấtkỳ cho trướctrênmàn plan). hình để hiểnthị hình ảnh (c) SE/FIT/HUT 2002 11 (c) SE/FIT/HUT 2002 12 2 Khoa CNTT – DHBK Hanoi hunglt@it-hut.edu.vn 8682595 Phép chiếu song song Parallel Projections Phép chiếu song song - Parallel Projections Phân loạiphépchiếusong songdựatrênhướng của tia chiếu Direction Of Projection và mặtphẳng chiếu- projection plane Phép chiếutrực giao (Orthographic projection) Ứng vớimỗimặtphẳng chiếutacó1 ma trậnchiếu tương ứng 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 [Ty ] = [T ] = [T ] = 0 0 1 0 x 0 0 1 0 z 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 1 (c) SE/FIT/HUT 2002 13 (c) SE/FIT/HUT 2002 14 Phép chiếutrụclượng (Axonometric) Trimetric Phép chiếutrụclượng SF- tỉ lệ co theo các trụclà: Phép chiếu Trimetric 2 2 fx = x'x +y'x trên cơ sở tỉ lệ co - SF của ảnh đốitượng trên mỗitrụclà 2 2 khác nhau. fy = x' y +y' y ' ' xx yx 0 1 1 0 0 1 2 2 x' y' 0 1 fz = x'z +y'z [U ] = 0 1 0 1 [T] = y y ' ' xz yz 0 1 0 0 1 1 0 0 0 1 (c) SE/FIT/HUT 2002 15 (c) SE/FIT/HUT 2002 16 Phép chiếuDimetric Là phép chiếu Trimetric với 2 hệ số tỉ lệ co bằng nhau, giá trị thứ 3 [T ] = [Ry][Rx][Pz] còn lạilàtuỳ ý. 2 '2 '2 2 2 2 cosφ 0 − sinφ 0 1 0 0 0 1 0 0 0 f = (x + y ) = sin φ +cos φsin ϕ z z z 0 1 0 0 0 cosϕ sinϕ 0 0 1 0 0 = . . sinφ 0 cosφ 0 0 − sinϕ cosϕ 0 0 0 0 0 2 '2 '2 2 f = (x + y ) = cos ϕ 0 0 0 1 0 0 0 1 0 0 0 1 y y y −1 f z cosφ sinφ sinϕ 0 0 φ = sin (± ) 2 0 cosϕ 0 0 2 − f [T ] = z sinφ − cosφ sinϕ 0 0 −1 f z 0 0 0 1 ϕ = sin (± ) 2 (c) SE/FIT/HUT 2002 17 (c) SE/FIT/HUT 2002 18 3 Khoa CNTT – DHBK Hanoi hunglt@it-hut.edu.vn 8682595 Phép chiếu Isometric 1 − 2sin 2 ϕ sin 2 φ = 1 − sin 2 ϕ sin 2 ϕ sin 2 φ = 1− sin 2 ϕ . sin2 ϕ 1/3 sin2 φ = = =1/2 1−sin2 ϕ 1−1/3 1 sin ϕ = ± 3 ϕ = ±35.260 φ = ±450 f = cos2 ϕ = 2 / 3 = 0.8165 (c) SE/FIT/HUT 2002 19 (c) SE/FIT/HUT 2002 20 Parallel Projections Phép chiếuxiên-Oblique Phép chiếu Cavalier Phép chiếu Cabinet orthographic oblique isometric axonometric (c) SE/FIT/HUT 2002 21 (c) SE/FIT/HUT 2002 22 Phép chiếu Cavalier f = 0, β = 900 phép chiếu sẽ trở thành phép chiếu trựcgiao. Còn với f = 1 kích thước 1 0 0 0 a = f cosα củahìnhchiếubằng kích 0 1 0 0 b = f sinα [T '' ] = thướccủa đốitượng => − a − b 0 0 cavalier 1 0 0 0 0 0 0 1 Phép chiếu Cavalier cho 0 1 0 0 [T ] = phép giá trị của α biến − f cosα − f sinα 0 0 đổimột cách tự do α = 300 và 450 0 0 0 1 (c) SE/FIT/HUT 2002 23 (c) SE/FIT/HUT 2002 24 4 Khoa CNTT – DHBK Hanoi hunglt@it-hut.edu.vn 8682595 Phép chiếuCabinet Oblique Projections Phép chiếuxiênvớihệ số co tỉ lệ f = 1/2 f β = cos −1 ( ) 12 + f 2 1 = cos −1 ( 2 ) = 63.4350 12 + (1 2) 2 D/2 D D Cabinet Projection D Cavalier Project (c) SE/FIT/HUT 2002 25 (c) SE/FIT/HUT 2002 26 Phép chiếuphốicảnh Perspective Projection Vanishing points Phép chiếu phốicảnh Each set of parallel lines (=direction) meets at a different point: The vanishing point for this direction Các đoạnthẳng song song củamôhình3D sauphépchiếuhộitụ tại1 điểmgọilà điểmtriệt tiêu - vanishing point Sets of parallel lines on the same plane lead to collinear vanishing points: the horizon for that plane Phân loại phép chiếu phốicảnh dựavàotâmchiếu-Centre Of Projection (COP) và mặtphẳng chiếu projection plane Easy examples corridor higher = further away Good way to spot faked images (c) SE/FIT/HUT 2002 27 (c) SE/FIT/HUT 2002 28 Điểm triệt tiêu Vanishing point Perspective Projections 3-point perspective điểm triệt tiêu quy tắc - principle vanishing point 1-point perspective The number of principal vanishing points is determined by the number of principal axes cut by the projection plane. If the plane only cut the z axis (most common), there is only 1 vanishing point. 2-points sometimes used in architecture and engineering. 3- points seldom used add little extra realism 2-point perspective (c) SE/FIT/HUT 2002 29 (c) SE/FIT/HUT 2002 30 5 Khoa CNTT – DHBK Hanoi hunglt@it-hut.edu.vn 8682595 Phép chiếuphốicảnh Phép biến đổiphốicảnh 1 0 0 0 0 1 0 0 [Tr] = 0 0 1 r 0 0 0 1 Phép chiếuphốica?nhcủa các điểmtrênđốitượng lên trên mặtphẳng 2D thu đượctừ phép chiếutrựcgiaovàphép biến đổiphốicảnh (c) SE/FIT/HUT 2002 31 (c) SE/FIT/HUT 2002 32 Perspective Projections Perspective Projections Consider a perspective projection with the viewpoint at the origin Tham số: and a viewing direction oriented along the positive -z axis and the view-plane located at z = -d centre of projection (COP) y yP y field of view (θ, φ) = ⇒ yP = z d z d projection direction a similar construction for xp up direction d ⇒ y x xP z d x 1 0 0 0x yP y y 0 1 0 0 y yp = ↔ = -z zP z d − z 0 0 −1 0 z − d 1 z d 0 0 1 d 01 1 divide by homogenous ordinate to map back to 3D space (c) SE/FIT/HUT 2002 33 (c) SE/FIT/HUT 2002 34 Perspective Projection Details Phép chiếuphốicảnh 1 tâm Giả sử khi mặtphẳng được đặttại z = 0 và tâm phép chiếunằmtrên x trục z , cách trụcz một khoảng zc = -1/r. xP z d x Nếu đốitượng cũng nằm trên mặtphẳng z = 0 thì đốitượng sẽ cho y y y P = ↔ hình ảnh thật. zP z d − z Phương trình biến đổi: 1 − d z d [ x y z 1 ][ Tr ] = [ x y z rz+1 ] 1 x 1 0 0 0x ma trậnbiến đổimột điểmphốicảnh [ Tr ] có dạng: y 0 1 0 0 y = − z 0 0 −1 0 z 1 0 0 0 PROJECTION perspective 1 0 0 0 0 1 matrix division 0 1 0 0 [ Tr ] = Flip z to transform to a left handed co-ordinate 0 0 1 r system ⇒ increasing z values mean increasing 0 0 0 1 distance from the viewer. (c) SE/FIT/HUT 2002 35 (c) SE/FIT/HUT 2002 36 6 Khoa CNTT – DHBK Hanoi hunglt@it-hut.edu.vn 8682595 phép chiếuphốicảnh 1 tâm Y’ Phép chiếuphốicVPả (y=10)nh 2 tâm VP ≡ y = 10 D’, H’C’, G’ y y’ D’ H’ C’,G’ VP( x = 10) D’ C’ VP 1 0 0 0 1 0 0 0 1 0 0 0 H G X=10 H’ G’ A’, E’B’, F’ 0 1 0 0 0 1 0 0 0 1 0 0 DC A’, E’B’, F’x’ = = E F 0 0 1 r 0 0 0 0 0 0 0 r x A’ E’ F’ B x 0 0 0 1 0 0 0 1 0 0 0 1 A B z 1 0 0 0 0 1 0 0 x y 1 0 0 p []x y z 1 = [x y 0 rz+1 ][]x' y' z' 1 = 0 1 1 0 0 p 0 0 0 r rz+1 rz+1 0 1 0 q 0 1 0 q [T ] = []x y z 1 = [x y z ( px + qy +1) ] 0 0 0 1 pq 0 0 1 0 0 0 1 0 0 0 0 1 0 0 0 1 (c) SE/FIT/HUT 2002 37 (c) SE/FIT/HUT 2002 38 x y z []x' y' z' 1 = 1 ( px + qy +1) ( px + qy +1) ( px + qy +1) Phép chiếuphốicảnh 3 tâm chiếu [ Tpqr ] = [Tp ][Tq ][Tr ] [ Tc ] = [ Tpq ][ Tz ] 1 0 0 p 1 0 0 0 1 0 0 p 1 0 0 p 1 0 0 0 1 0 0 0 1 0 0 p 0 1 0 0 0 1 0 q 0 1 0 0 0 1 0 q 0 1 0 q 0 1 0 0 0 1 0 q = = = = 0 0 1 0 0 0 1 0 0 0 1 r 0 0 1 r 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 2 tâm chiếu: 1 0 0 p [ -1/p 0 0 1 ] 0 1 0 q []x y z 1 = [x y z ( px + qy + rz +1) ] [ 0 -1/q 0 1 ] 0 0 1 r VP (Vanishing point) tương ứng trên 2 trụcxvàylàđiểm: [ 0 0 0 1 1/p 0 0 1 ] và [ 0 1/q 0 1 ]. (c) SE/FIT/HUT 2002 39 (c) SE/FIT/HUT 2002 40 x y z []x' y' z' 1 = 1 ( px + qy + rz +1) ( px + qy + rz +1) ( px + qy + rz +1) y' 3 tâm chiếu: VP ( y = 10) y' trên trụcxtại điểm [ -1/p 0 0 1 ], H' ytại điểm [ 0 -1/q 0 1 ] D' D' ztại điểm [ 0 0 -1/r 1 ]. H' G' C' VP sẽ tương ứng với các giá trị : G' E' C' [ 1/p 0 0 1 ], [ 0 1/q 0 1 ] [ 0 0 1/r 1 ] [ Tc ] = [ Tpqr ][ Tz ] VP ( x = 10 ) VP ( z = 10 ) F' 1 0 0 p 1 0 0 0 1 0 0 p A' x' 0 1 0 q 0 1 0 0 0 1 0 q z' = . = x' 0 0 1 r 0 0 0 0 0 0 0 r A', E' F' B' B' 0 0 0 1 0 0 0 1 0 0 0 1 (c) SE/FIT/HUT 2002 41 (c) SE/FIT/HUT 2002 42 7 Khoa CNTT – DHBK Hanoi hunglt@it-hut.edu.vn 8682595 Phân loại các phép chiếu (c) SE/FIT/HUT 2002 43 8
File đính kèm:
 bai_giang_do_hoa_hien_thuc_ao_bai_5_nguyen_ly_ve_3d_va_phep.pdf
bai_giang_do_hoa_hien_thuc_ao_bai_5_nguyen_ly_ve_3d_va_phep.pdf

