Bài giảng Đồ họa hiện thực ảo - Bài 4b: Phép biến đổi trong không gian - Lê Tấn Hưng
Ma trận biến đổi 3 chiều
3D Matrix Transformations
Các phép biến đổi chuyển vị - translation, tỉ lệ-scaling và
quay-rotation sử dụng trong không gian 2D đều co thể mở
rộng trong không gian 3D
Again, using homogeneous coordinates it is possible to
represent each type of transformation in a matrix form
In 3D, each transformation is represented by a 4x4 matrix

Trang 1

Trang 2

Trang 3
Trang 4

Trang 5
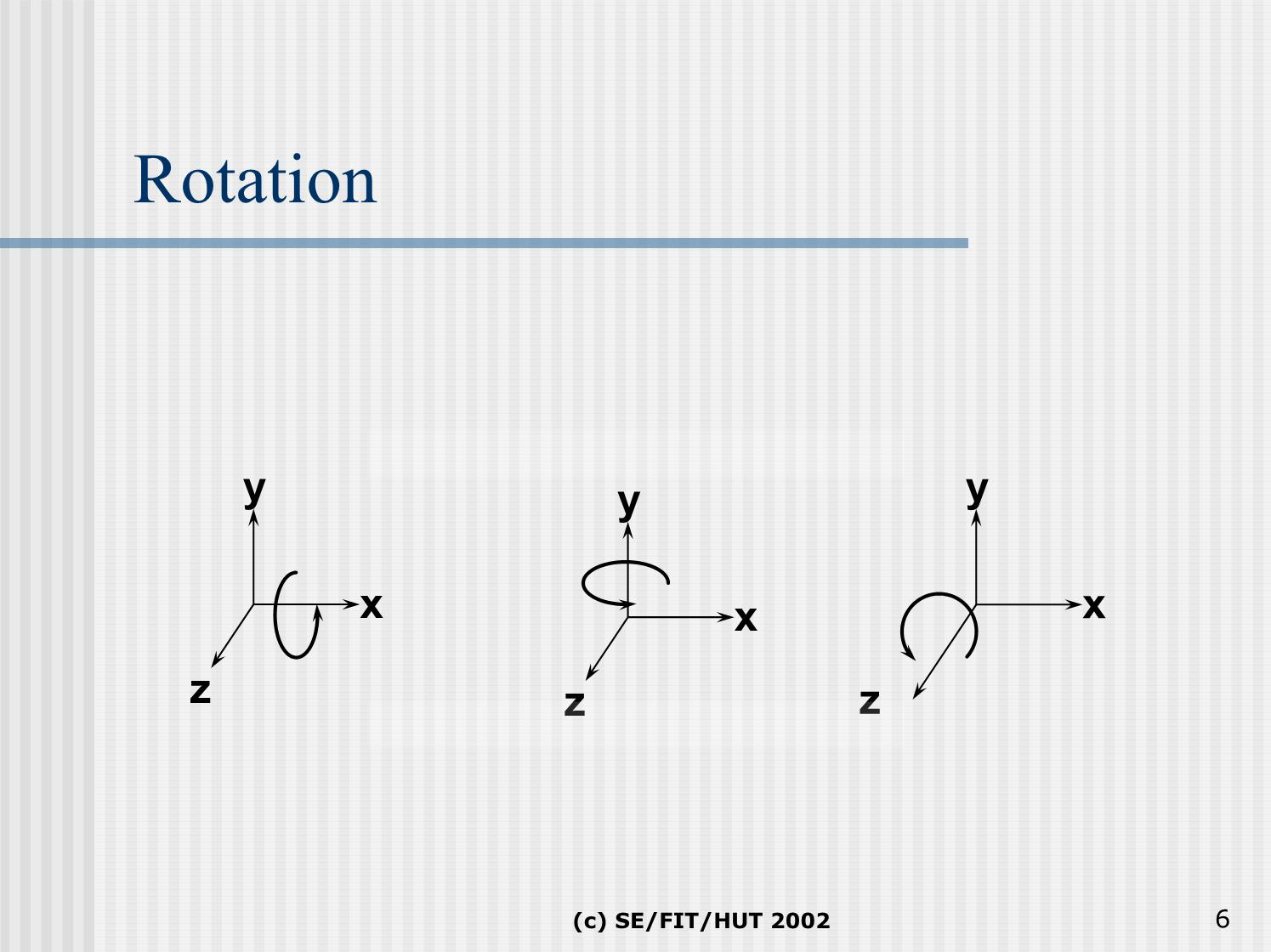
Trang 6

Trang 7
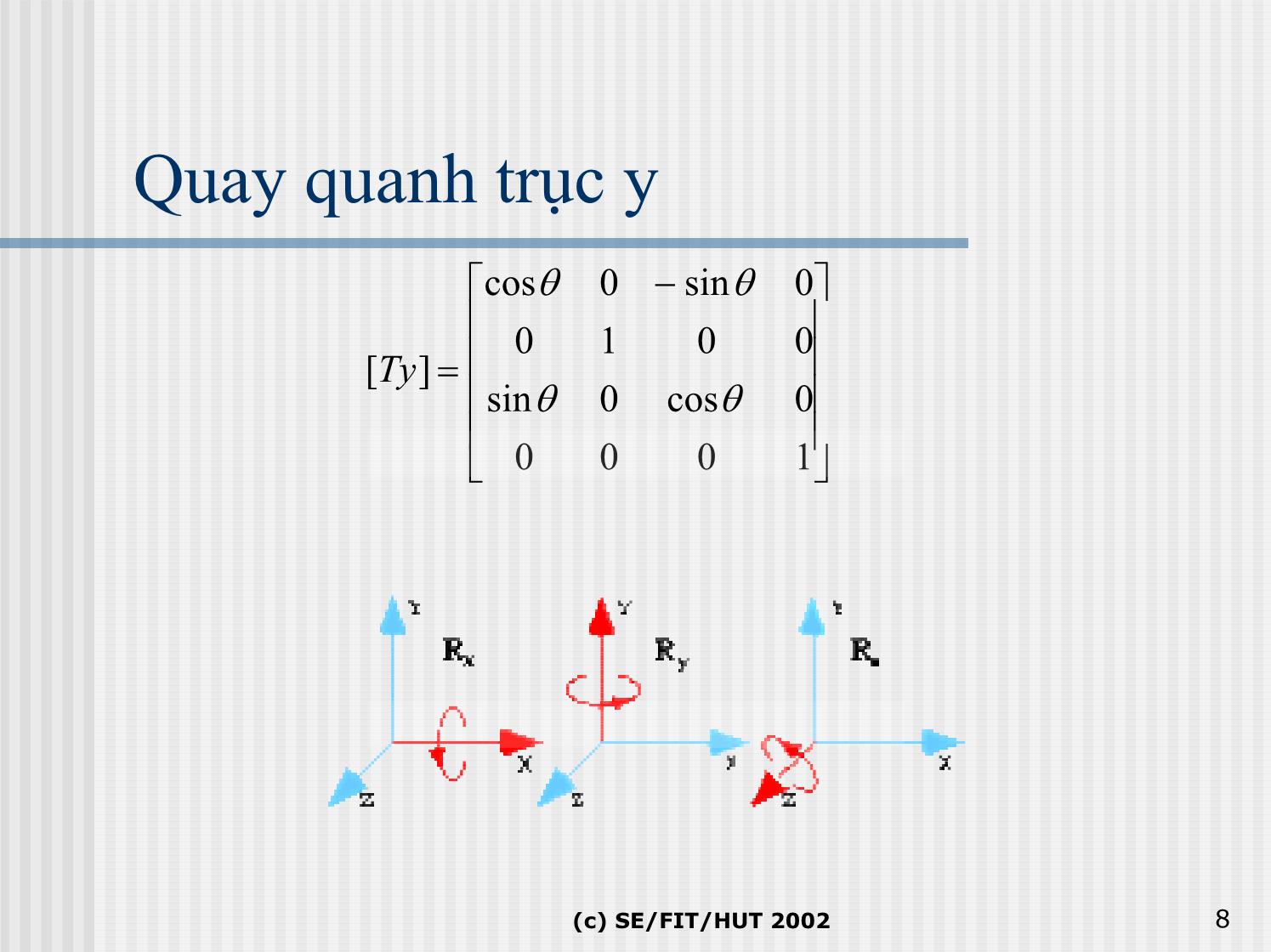
Trang 8
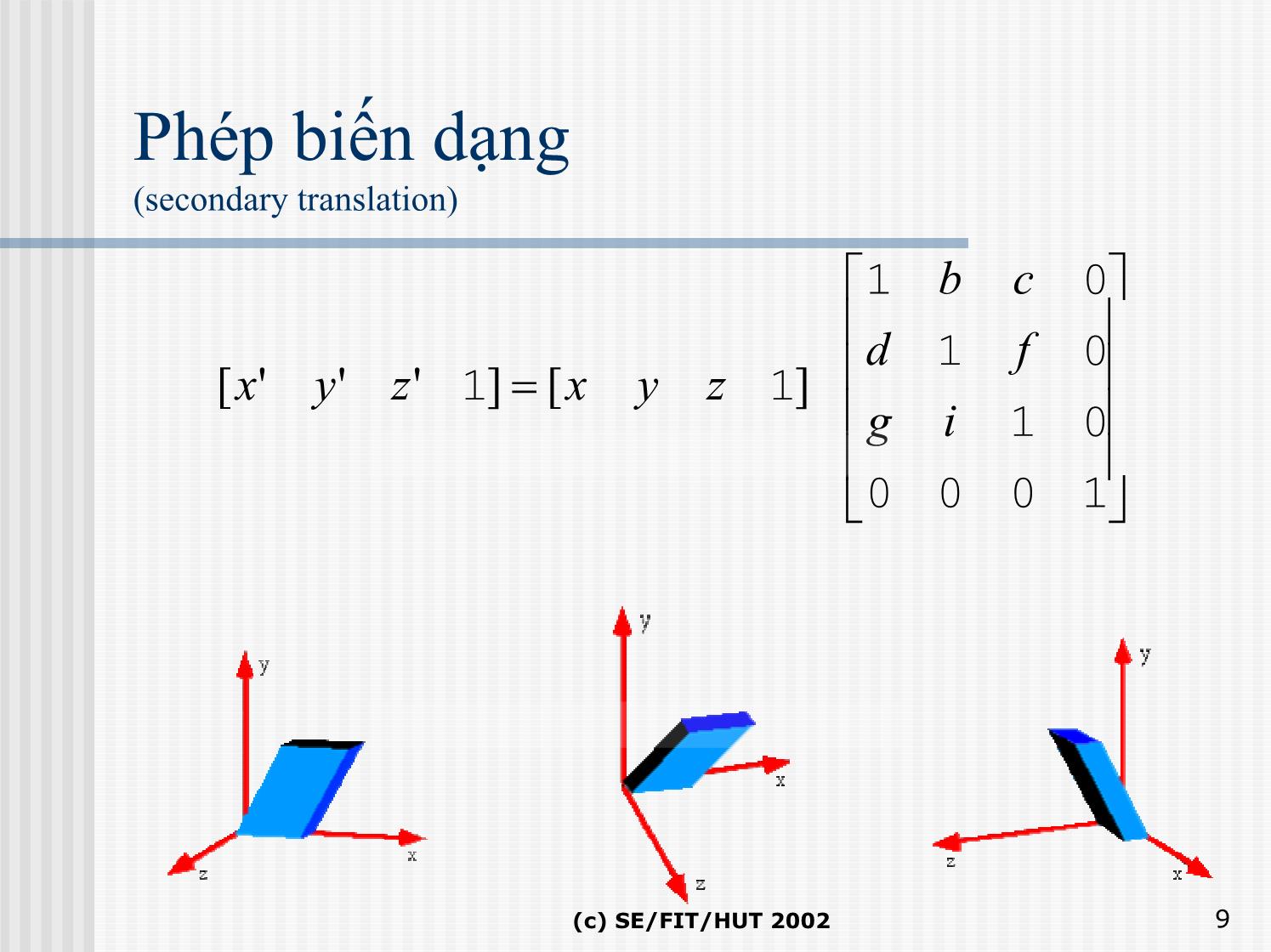
Trang 9
Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Đồ họa hiện thực ảo - Bài 4b: Phép biến đổi trong không gian - Lê Tấn Hưng", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Đồ họa hiện thực ảo - Bài 4b: Phép biến đổi trong không gian - Lê Tấn Hưng

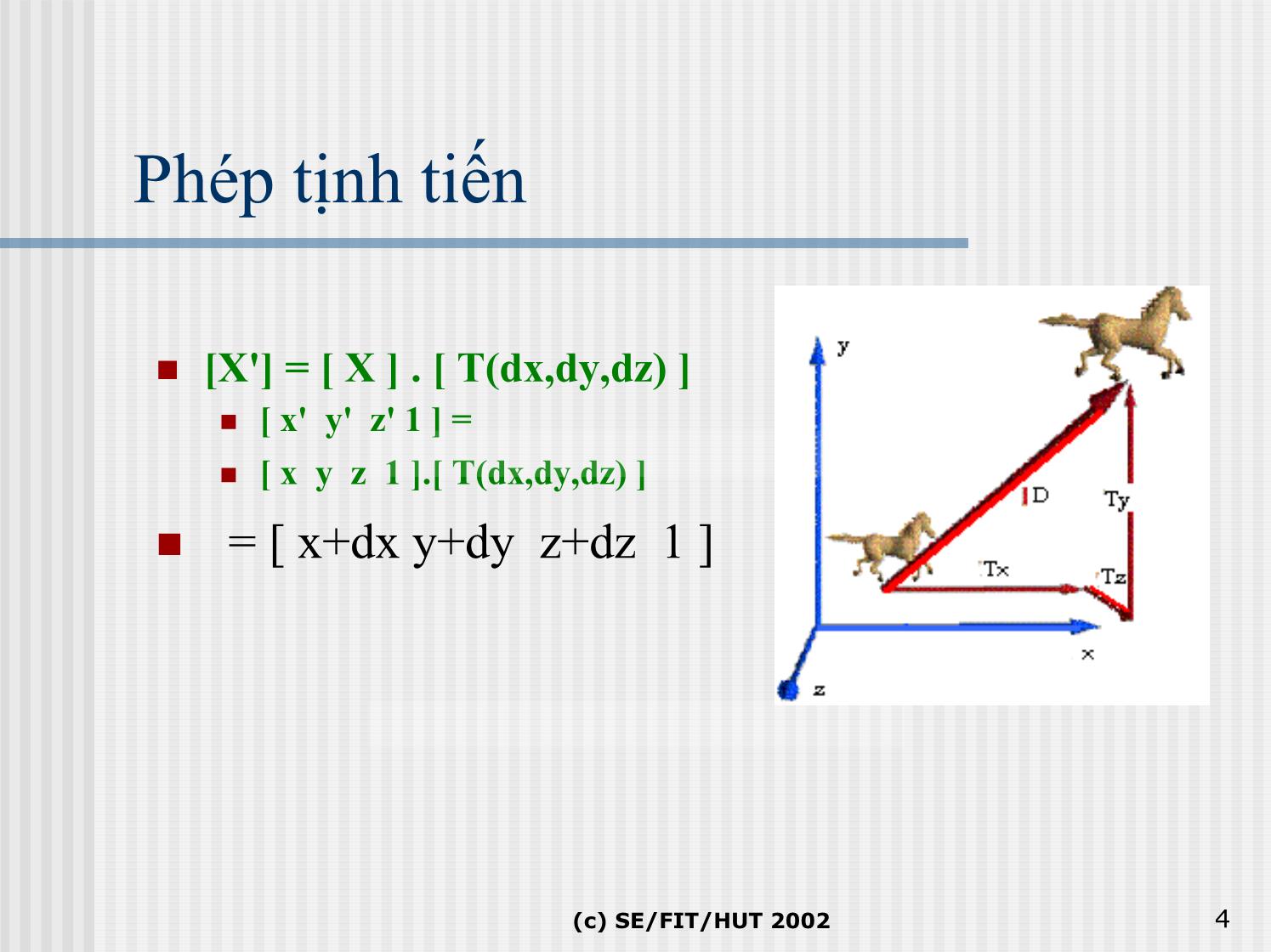
Bài 4B: Phép biến đổi trong không gian (c) SE/FIT/HUT 2002 1 Ma trận biến đổi 3 chiều 3D Matrix Transformations Các phép biến đổi chuyển vị - translation, tỉ lệ-scaling và quay-rotation sử dụng trong không gian 2D đều co thể mở rộng trong không gian 3D Again, using homogeneous coordinates it is possible to represent each type of transformation in a matrix form In 3D, each transformation is represented by a 4x4 matrix (c) SE/FIT/HUT 2002 2 Các phép biến đổihìnhhọc3 chiều Biểudiễn điểm trong không gian 3 chiều • [ x* y* z* h ] = [ x y z 1 ]. [ T ] • [x' y' z' 1 ]= [ x*/h y*/h z*/h 1 ][ T ] Ma trậnbiến đổi a b c p d e f q [T ] = g i j r l m n s (c) SE/FIT/HUT 2002 3 Phép tịnh tiến [X'] = [ X ] . [ T(dx,dy,dz) ] [ x' y' z' 1 ] = [ x y z 1 ].[ T(dx,dy,dz) ] = [ x+dx y+dy z+dz 1 ] (c) SE/FIT/HUT 2002 4 Phép tỉ lệ = [x .s1 y .s2 z .s3 1] • s1, s2, s3 là các hệ số tỉ lệ tương ứng trên các trụctoạđộ (c) SE/FIT/HUT 2002 5 Rotation y y y x x x z z z (c) SE/FIT/HUT 2002 6 Phép quay 3 chiều Quay quanh các trụctoạđộ • Quay quanh trụcx • Quay quanh trụcz (c) SE/FIT/HUT 2002 7 Quay quanh trụcy cosθ 0 − sinθ 0 0 1 0 0 [Ty] = sinθ 0 cosθ 0 0 0 0 1 (c) SE/FIT/HUT 2002 8 Phép biếndạng (secondary translation) 1 b c 0 d 1 f 0 [x' y' z' 1] = [x y z 1] g i 1 0 0 0 0 1 (c) SE/FIT/HUT 2002 9 Phép lấy đốixứng (reflections-secondary translation) (c) SE/FIT/HUT 2002 10 Quay quanh mộttrụcbấtkỳ song song vớicác trụctọa độ 1 0 0 0 1 0 0 0 0 1 0 0 0 cosφ sin φ 0 [Tr ] = [T (φ)] = 0 0 1 0 0 − sin φ cosφ 0 , 0 0 0 1 , 0 y z 1 1 0 0 0 1 0 0 0 0 cosφ sinφ 0 0 1 0 0 [Tth]= [Tr]−1 = 0 −sinφ cosφ 0 0 0 1 0 0 y(1−cosφ)+zsinφ z(1−cosφ)−ysinφ 1 0 − y − z 1 (c) SE/FIT/HUT 2002 11 Quay quanh mộttrụcbấtkỳ (c) SE/FIT/HUT 2002 12 Solution Chuyển P1 về gốctọa độ. Quay quanh trục y sao cho P1P2 nằmtrênmặtphẳng (y, z) Quay quanh trục x sao cho P1P2 trùng vớitrụcz. Quay quanh trục z sao cho P1P3 nằmtrênmặtphẳng (y, z) Euler’s Theorem: Every rotation around the origin can be decomposed into a rotation around the x-axis followed by a rotation around the y-axis followed by a rotation around the z-axis. (c) SE/FIT/HUT 2002 13 Bước1: ChuyểnP1 về gốctọa độ 1 0 0 0 0 1 0 0 [T (−x1,−y1,−z1)] = 0 0 1 0 − x1 − y1 − z1 1 y y P3 P3 P2 P1 P2 p P1 z z x x (c) SE/FIT/HUT 2002 14 Bước 2: Quay quanh trụcy cos( - 90 + φ) = sinφ = z'2/L = ( z2 - z1)/L sin( - 90 + φ) = - cosφ = x'2/L = ( x2 - x1)/L y 2 2 2 2 L = (z'2 ) (x'2 ) = (z2 −z1) (x2 −x1) P3 [ P''2 ] = [ P'2 ][ T(φ-90) ] P'2(x'2,y'2,z'2) = [ 0 y2-y1 L ] P'1 L φ z(x'2,0,z'2)x (c) SE/FIT/HUT 2002 15 Bước 3: Quay quanh trục x. cos ϕ = z''2/N, sin ϕ = y''2/N y Với N = | P''1P''2| là độ dài của đoạn P''1P''2 P''2 N P''1 ''' ϕ [P 2] = [P''2][T(ϕ)] = [P'2][T(φ-90)][T(ϕ)] x = [P2 ][T(-x1,-y1,-z1 ][T(φ-90)][T(ϕ)] z = [ 0 0 |P1P2| 1 ] (c) SE/FIT/HUT 2002 16 Bước 4: Quay quanh trụcz ''' [P 3]= [P3 ][T(-x1,-y1,-z1 ][T(φ-90)][T(ϕ)] Với góc quay dương ψ trên trụcz ''' ''' cos ψ = y3 /M; sin ψ = x3 /M; Ma trậntổng hợpcủa các phép biến đổi[ T ] có dạng sau đáp ứng toàn bộ quá trình biến đổiquay đốitượng quanh mộttrụcbấtkỳ. y y''' [ T ] = [T(-x1,-y1,-z1)][T(φ-90)][T(ϕ)][T(ψ)] 3 P'''3 ψ M x'''3 P'''2P'''1 x z (c) SE/FIT/HUT 2002 17 Kếtquả sau biến đổicầnphải đưavề vị trí ban đầu qua các phép biến đổi ngược. [Tth]= [T(-x1,-y1,-z1)]x[T(φ-0)]x[T(ϕ)]x [T(ψ)]x[T(ψ)]x[T(ϕ)]x [T(φ-90)]x[T(-x1,-y1,-z1)] (c) SE/FIT/HUT 2002 18 Hệ toạ độ Coordinate Frame y j φ i k z x Coordinate frame is given by origin φ and three mutually orthogonal unit vectors, i, j, k. Mutually orthogonal (dot products): i•j = ?; i•k = ?; j•k = ?. Unit vectors (dot products): i•i = ?; j•j = ?; k•k = ?. (c) SE/FIT/HUT 2002 19 Orientation Right handed coordinate system: Left handed coordinate system: k y y j j φ i i φ k z x z x Cross product: i x j = ? Cross product: i x j = ? (c) SE/FIT/HUT 2002 20 Coordinate Transformations y j i φ k z x Transform (x, y, z, 0) coordinate frame to (i, j, k, φ) coordinate frame. Affine transformation matrix: ix jx kx φx i j k φ y y y y . iz jz kz φz 0 0 0 1 Maps (i, j, k, φ) coordinates into (x, y, z, 0) coordinates! (c) SE/FIT/HUT 2002 21 Coordinate change (Translation) b y (φx, φy, φz) a (0,0,0) z c x Change from (a,b,c,φ) coordinates to x a (x,y,z,0) coordinates: y b = . z c 1 0 0 0 1 1 (c) SE/FIT/HUT 2002 22 Coordinate change (Rotation) b y x θ (φx, φy, φz) (0,0,0) a c z Change from (a,b,c,φ) coordinates to x a (x,y,z,0) coordinates: y b = . z c 1 0 0 0 1 1 (c) SE/FIT/HUT 2002 23 Composition of coordinate change y’’ y’ M2 y φ’’ z’’ M1 x’ φ’ x’ ’ ’ φ z z x M1 changes from coordinate frame (x,y,z,θ) to (x’,y’,z’,θ’). M2 changes from coordinate frame (x’,y’,z’,θ’) to (x’’,y’’,z’’,θ’’). Change from coordinate frame (x,y,z,θ) to (x’’,y’’,z’’,θ’’): ? (c) SE/FIT/HUT 2002 24 Object vs. coordinate transformations Translate and then rotate object: y y y φ φ φ z x z x z x Translate and then rotate coordinate frame: y y y’ y y’’ φ x’’ φ φ’ φ ’’ z x φ z z’ x x’ x z z’’ (c) SE/FIT/HUT 2002 25 Object vs. coordinate transformations (2) Translate and then rotate object: y y y φ φ φ z x z x z x Rotate and then translate coordinate frame: y’’ y y’y y x’’ φ’’ φ x’ φ φ ’’ ’ z z x z φ x z’ z x (c) SE/FIT/HUT 2002 26 Order of transformations Let Mi be the transformation matrix for transformation Ti. Sequence of object (point) transformations, T1, T2, T3. Transformation matrix = M3 x M2 x M1. Sequence of coordinate system transformations, T1, T2, T3. Transformation matrix = M1 x M2 x M3. Note: OpenGL, OpenInventor use coordinate system transformations. (c) SE/FIT/HUT 2002 27
File đính kèm:
 bai_giang_do_hoa_hien_thuc_ao_bai_4b_phep_bien_doi_trong_kho.pdf
bai_giang_do_hoa_hien_thuc_ao_bai_4b_phep_bien_doi_trong_kho.pdf

