Bài giảng Đồ họa hiện thực ảo - Bài 4a: Các phép biến đổi Đồ hoạ - Lê Tấn Hưng
Ví dụ
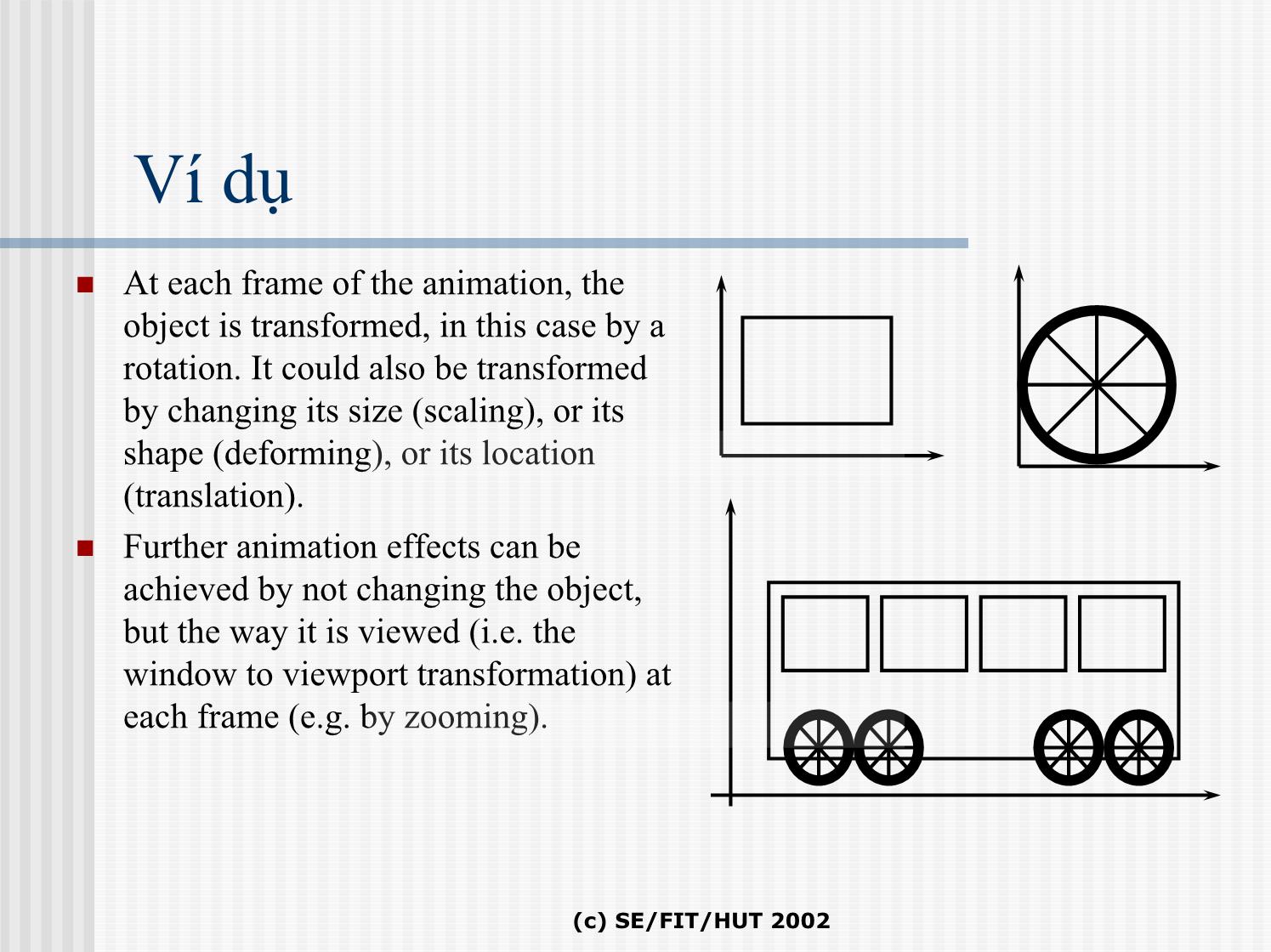
At each frame of the animation, the
object is transformed, in this case by a
rotation. It could also be transformed
by changing its size (scaling), or its
shape (deforming), or its location
(translation).
Further animation effects can be
achieved by not changing the object,
but the way it is viewed (i.e. the
window to viewport transformation) at
each frame (e.g. by zooming).

Trang 1

Trang 2
Trang 3
Trang 4
Trang 5
Trang 6

Trang 7
Trang 8
Trang 9

Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Đồ họa hiện thực ảo - Bài 4a: Các phép biến đổi Đồ hoạ - Lê Tấn Hưng", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Đồ họa hiện thực ảo - Bài 4a: Các phép biến đổi Đồ hoạ - Lê Tấn Hưng

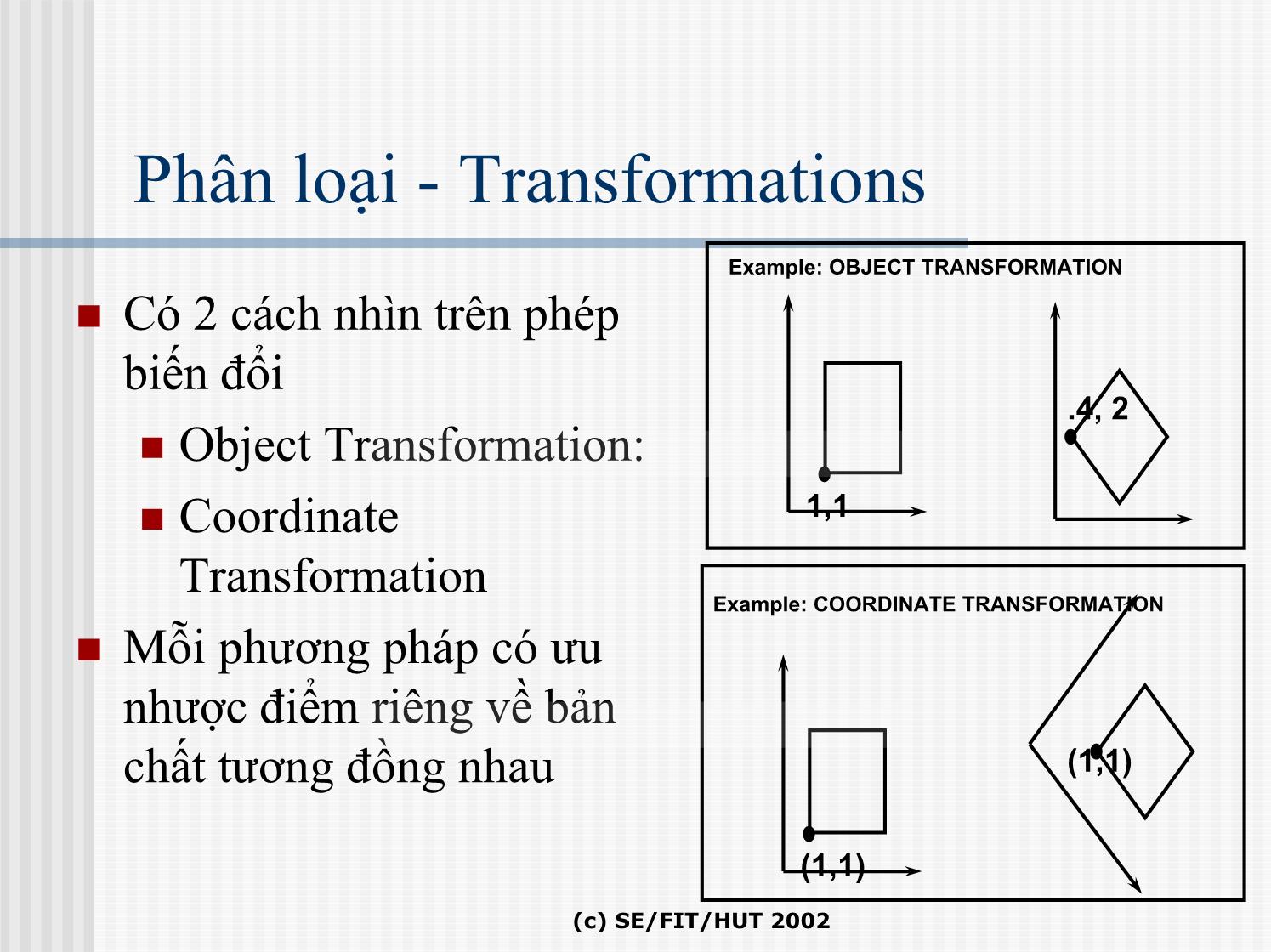
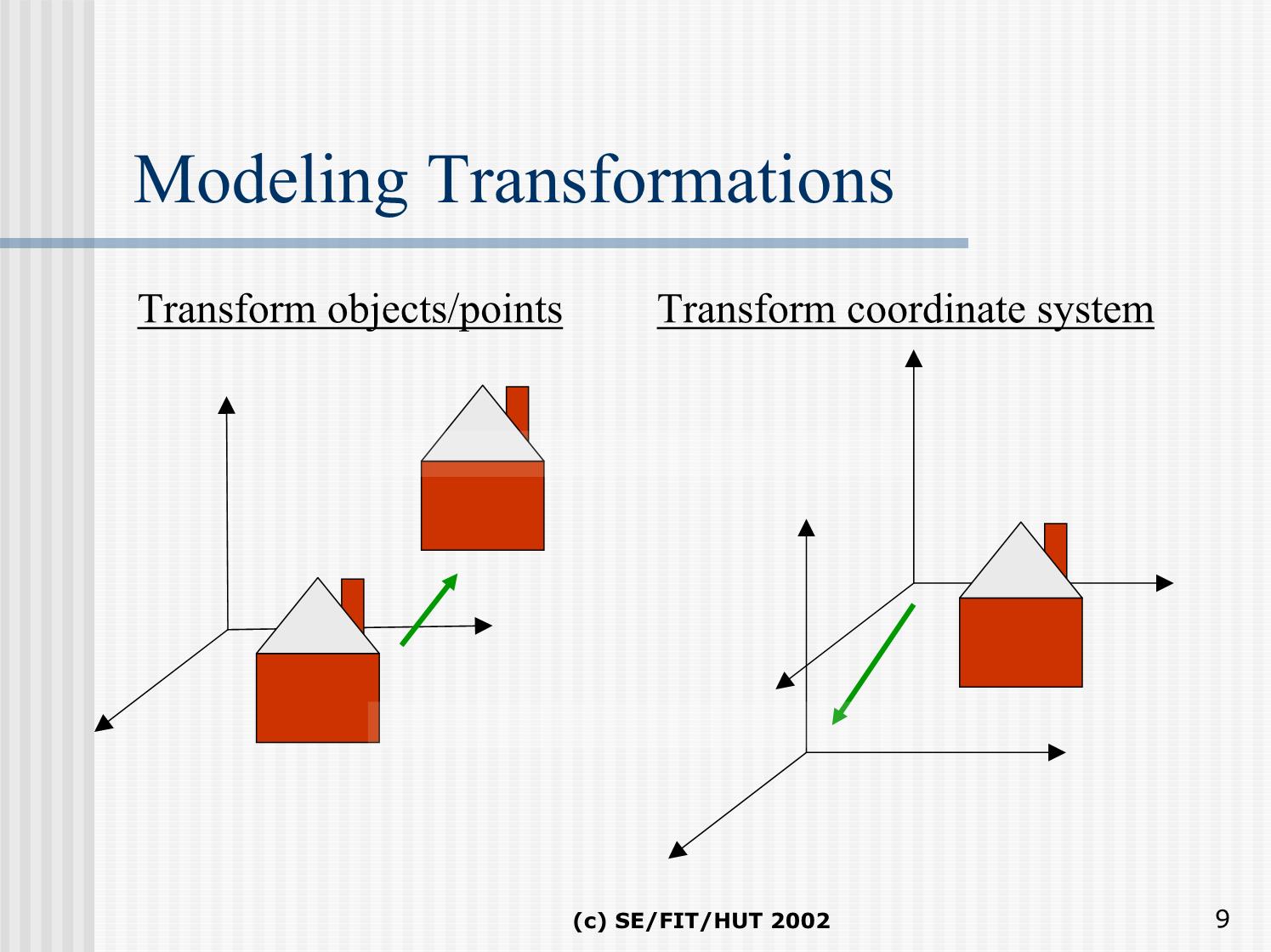
Bài 4 Các phép biến đổi Đồ hoạ Affine Transformations I KHái niệm cơ bản Le Tan Hung Email: hunglt@it-hut.edu.vn II Các phép biến đổi III Hệ tọa độ đồng nhất (c) SE/FIT/HUT 2002 1 Mô hình hoá - Modelling mô hình - model : Modeling - Mô hình hoá Thực thể cơ sở - primitives object như circles, lines polygons hay cubes Cảnh - A scene mô hình hoá cảnh - Scene Modeling A scene with several instances of the object (c) SE/FIT/HUT 2002 2 Ví dụ At each frame of the animation, the object is transformed, in this case by a rotation. It could also be transformed by changing its size (scaling), or its shape (deforming), or its location (translation). Further animation effects can be achieved by not changing the object, but the way it is viewed (i.e. the window to viewport transformation) at each frame (e.g. by zooming). (c) SE/FIT/HUT 2002 Phép biến đổi - Transformations Trong kỹ thuật đồ hoạ 3 bước: modeling, rendering, displaying Với Modeling: modeling world viewing coordinate Modeling coordinate Viewing coordinate (eye coordinate) transformation transformation Phép biến đổi - Transformation Biến đổi mô hình hoá - Modeling transformations Biến đổitạo góc nhìn - Viewing transformations Biến đổitạoHoạtcảnh - Animation (c) SE/FIT/HUT 2002 4 Transformations - Modeling world (c) SE/FIT/HUT 2002 5 Viewing Transformations - Viewing Viewing Transformations - Viewing CAMERA OBJECT Trong phép biến đổi này : Một mô hình có thể quan sát trên các góc cạnh khác nhau (e.g. faraway, near, looking down, looking up) WORLD (c) SE/FIT/HUT 2002 6 Phép biến đổiAffine Affine Transformations? Phép biến đổi Affine Ví dụ: phép biến đổitọa độ vớichỉ 2 điểm đầucuốicủa đoạnthẳng tạo thành 2 điểmmớimàkhinối chúng với nhau tạothànhđoạnthẳng mới. Các điểmnằmtrênđoạnthẳng sẽ có kếtquả là điểm nằmtrênđoạnthẳng mớivới cùng phép biến đổi thông qua phép nộisuy. (c) SE/FIT/HUT 2002 7 Phân loại - Transformations Example: OBJECT TRANSFORMATION Có 2 cách nhìn trên phép biến đổi .4, 2 Object Transformation: Coordinate 1,1 Transformation Example: COORDINATE TRANSFORMATION Mỗi phương pháp có ưu nhược điểm riêng về bản chất tương đồng nhau (1,1) (1,1) (c) SE/FIT/HUT 2002 Modeling Transformations Transform objects/points Transform coordinate system (c) SE/FIT/HUT 2002 9 2D Object Transformations A 2D object transformation alters each point P into a new point Q using a specific formula or algorithm. It therefore alters the co-ordinates of P (Px,Py) into new values which specify point Q (Qx,Qy) This can be expressed using some function T, that maps co-ordinate pairs into co-ordinate pairs: (c) SE/FIT/HUT 2002 Matrix Representation If affine transformation T maps P onto Q, then Q is related to P as follows: where a, b, c, d, tx and ty are all constants, and ad = bc This gives rise to the following matrix representation: Q a b P t x x x i.e. = + Q y c d P y t y (c) SE/FIT/HUT 2002 Các phép biến đổihìnhhọc hai chiều Phương pháp biểudiễn đốitượng P = [ x y ] Phép biến đổivị trí điểm a b T = c d Thực thi phép biến đổi đúng trên 1 điểm ảnh sẽđúng trên toàn bộđối tượng y pW pM x z (c) SE/FIT/HUT 2002 12 y Phép biến đổi Phép bấtbiến z x Phép biến đổitỉ lệ - Scaling A scaling changes the size of an object with two scale factors, Sx and Sy Phép biếndạng A shearing shears an object in a particular direction, (in 2D, it’s either in the x or in the y direction (c) SE/FIT/HUT 2002 13 Phép quay- Rotation y ( x’, y’ ) ρ ( x, y ) ρ θ α x (c) SE/FIT/HUT 2002 14 Thuộc tính cơ bản của phép biến đổi Affine Transformations Preservation of lines: Affine transformations map lines to lines; Preservation of parallelism Preservation of proportional distances Affine transformations change volume by | Det(M) |; (c) SE/FIT/HUT 2002 15 Kếthợpcácphépbiến đổi Composition of Affine Transforms Any affine transformation can be decomposed into elementary transformations. Mọi phép biến đổiphứctạp đềucó thể tạo thành từ các phép biến đổicơ sở như: Dịch chuyển-Translation Tỉ lệ - Scaling Quay- Rotation Biếndạng - Shearing (c) SE/FIT/HUT 2002 Affine transformations preserve affine combinations It is rare that we want to perform just one elementary transformation. Usually an application requires that we build a complex transformation out of several elementary ones e.g. translate an object, rotate it, and scale it, all in one move These individual transformations combine into one overall transformation This is called the composition of transformations. The composition of two or more affine transformations is also an affine transformation (c) SE/FIT/HUT 2002 Thuộc tính T Tác động lên tập các điểm đặc trưng của đối tượng tạo thành phép biến đổi cho đối tượng We have defined each transformation by their effects on single points In practice these will be applied to multiple points to transfer entire scenes or objects made up of many defining points (c) SE/FIT/HUT 2002 18 Điểm gốc - Pivotal points Cho phép quay và tỉ lệ Rotation and Scaling The simple versions of rotation and scaling have been based around the origin. This means that when we rotate or scale, the object will also move, with respect to the origin Translate all points through (-c1,-c2) Rotate all points about the origin by Translate all points back through (c1,c2) (c1,c2) (0,0) (c) SE/FIT/HUT 2002 Pivotal points Often we wish to rotate or scale with respect to some pivotal point, not the origin Most significantly, we often wish to rotate or scale an object about its centre, or midpoint In this way, the object’s location does not change To do this, we relate the rotation or scaling about the pivotal point V, to an elementary rotation or scaling about the origin We first translate all points so that V coincides with the origin We then rotate or about the origin then all points are translated back, so that V is restored to its original location (c) SE/FIT/HUT 2002 Hệ toạ độ đồng nhất Vấn đề gặp phải: An affine transformation is composed of a linear transformation followed by a translation Unfortunately, the translation portion is not a matrix multiplication but must instead be added as an extra term, or vector What we need is a “trick”, so that translations can be represented in matrix multiplication form This then means that they can be easily composed with other transformations, by simply multiplying the matrices together (c) SE/FIT/HUT 2002 Tọa độ đồng nhất Homogeneous Transform x' = ax + by + n y' = bx + dy + m Phương pháp biểudiễnmở rộng thông qua tọa độ đồng nhấtcủa các vector vị trí Với ứng dụng của phép chiếuhìnhhọcmàởđótọa độ điểm đượcmôtả dướima trận [ x* y* h] với x = x*/h, y = y*/h, z = z*/h và h là mộtsố thựctuỳ ý (c) SE/FIT/HUT 2002 22 Ưu điểmcủaHệ tọa độ đồng nhất Homogeneous Transform Ðưa ra cái nhìn hợpnhấtcủa các phép biến đổidưới phép nhân ma trận, hỗ trợ cho việcxử lý bằng cả phầncứng và phầnmềm Kếthợp các các phép biến đổitạo thành ma trậntíchđơngiảnduy nhất. Tránh nhầmlẫnvề thứ tự của các phép nhân khi sử dụng. Order matters: AB is generally not the same as BA Cho phép kếthợpvớicả các phép biến đổi đặcbiệt không tuyến tính khác(non-affine) như: Phép chiếuphốicảnh - Perspective projections! Uốn - Bends, Vuốt tapers v.v.v (c) SE/FIT/HUT 2002 23 Phép biến đổivớitọa độ đồng nhất Ma trậnbiến đổi đồng nhất a b 0 [T ] = c d 0 Phép tịnh tiến m n 1 1 0 0 [x' y' 1] = [x y 1] 0 1 0 = [x + m y + n 1] m n 1 (tx, ty, tz) (c) SE/FIT/HUT 2002 24 Phép tỉ lệ S1 0 0 [x' y' 1] = [x y 1] 0 S2 0 = [x.S1 y.S2 1] 0 0 1 (c) SE/FIT/HUT 2002 25 Phép quay y ( x’, y’ ) = [x.cosφ − y.sinφ x.sinφ + y.cosφ 1] ρ ( x, y ) ρ θ α x (c) SE/FIT/HUT 2002 26 Phép biến đổitổng hợp (c) SE/FIT/HUT 2002 27 Phép chuyển đổi (c) SE/FIT/HUT 2002 28 Windows and Viewports Mapping involves scaling and translation (moving). Both the world window and viewport can be any aligned rectangle. Usually the viewport is set to take up the entire screen window. (c) SE/FIT/HUT 2002 29 Phép biến đổitheoma trận Ma trận chuyểnvị theo Window Xvmax- Xvmin 0 0 Xwmax- Xwmin Ma trậnbiến đổitỉ lệ Yv max−Yv min [S1] = 0 0 Ywmax−Ywmin 0 0 1 Ma trận chuyểnvị theo tọa độ viewport (c) SE/FIT/HUT 2002 30 Ma trậnbiến đổitổng hợpcủa phép chuyển đổi tọa độ [T] = [T1]x[S1]x[T2] Xvmax- Xvmin 0 0 Xwmax- Xwmin Yvmax−Yvmin [T] = 0 0 Ywmax−Ywmin Xvmax- Xvmin Yvmax−Yvmin Xvmin− Xwmin Yvmin−Ywmin 1 Xwmax- Xwmin Ywmax−Ywmin (c) SE/FIT/HUT 2002 31 Coordinate Transforms (c) SE/FIT/HUT 2002 Coordinate Transforms x u u’ (1,1) (1,1) v v’ Object defined in Local Coordinate System y Object after transformation in Global Coordinate System (c) SE/FIT/HUT 2002 33 Identity as a Coordinate Transform x x u u’ (1,1) (1,1) v y v’ y 1 0 0 Q = 0 1 0P 0 0 1 (c) SE/FIT/HUT 2002 34 Translation x u 1 0 tx x u’ Q = 0 1 tyP (1,1) (1+tx,1+ty) 0 0 1 v y v’ y 1 0 tx0 tx 1 0 tx1 1+ tx 1 0 tx0 tx 0 1 ty0 = ty 0 1 ty0 = ty 0 1 ty1 = 1+ ty 0 0 1 1 1 0 0 1 1 1 0 0 1 1 1 origin (c) SE/FIT/HUT 2002 35 0 Rotation O = 0 x u x 1 u’ (1,1) v’ v y y cosθ − sinθ 0 cosθ − sinθ v = sinθ u = cosθ Q = sinθ cosθ 0P 1 1 0 0 1 (c) SE/FIT/HUT 2002 36 Scaling u x u x (sx*1,sy*1) (1,1) v y y v sx 0 0 0 sx 0 Q = 0 sy 0P u = sy O = 0 v = 0 0 0 1 1 1 1 (c) SE/FIT/HUT 2002 37 Composite Transformations x x x1(1− cosθ ) + y1 sinθ u y (1− cosθ ) − y sinθ O = 1 1 (1,1) 1 u’ v ’ cosθ + x1(1−cosθ)+ y1 sinθ v y sinθ + y (1−cosθ)− y sinθ y v = 1 1 1 cosθ − sinθ x (1− cosθ ) + y sinθ 1 1 −sinθ + x1(1−cosθ)+ y1 sinθ M = sinθ cosθ y1(1− cosθ ) − x1 sinθ u = cosθ + y1(1−cosθ)− y1 sinθ 0 0 1 1 (c) SE/FIT/HUT 2002 38 Modeling Transformations To make full use of the computational optimisation made possible by composite transforms, we only want to apply the transformations to points at the very end i.e. the transformation operation (multiplying point p by transform matrix is the very last thing we do in the modelling phase) Specify Specify points Send to Transformations in local coords (composite if necessary) Pipeline (c) SE/FIT/HUT 2002 39 + + This of course shouldn’t = mean all objects need to share the same transformations (c) SE/FIT/HUT 2002 40 + + + + transform transform transform Obviously we want something more versatile = (c) SE/FIT/HUT 2002 41
File đính kèm:
 bai_giang_do_hoa_hien_thuc_ao_bai_4_cac_phep_bien_doi_do_hoa.pdf
bai_giang_do_hoa_hien_thuc_ao_bai_4_cac_phep_bien_doi_do_hoa.pdf

