Bài giảng Đồ họa hiện thực ảo - Bài 2: Các giải thuật sinh các thực thể cơ sở - Lê Tấn Hưng

Bài 2:
 Các giảithuậtsinh 
 các thực thể cơ sở
 Le Tan Hung
 hunglt@it-hut.edu.vn
 (c) SE/FIT/HUT 2002
Giảithuậtxâydựng các
thựcthể cơ sở
„ Giảithuậtsinhđường thẳng – Line
„ Giảithuậtsinhđường tròn - Circle
„ Giảithuật VanAken sinh Ellipse
„ Giảithuậtsinhđagiác
„ Giảithuậtsinhkýtự
 (c) SE/FIT/HUT 2002 2
Rờirạchoáđiểm ảnh
(Scan Conversion rasterization)
„ Scan Conversion rasterization
„ Tính chất các đốitượng cần đảmbảo:
 „ smooth
 „ continuous
 „ pass through specified points
 „ uniform brightness
 „ efficient
 (c) SE/FIT/HUT 2002 3
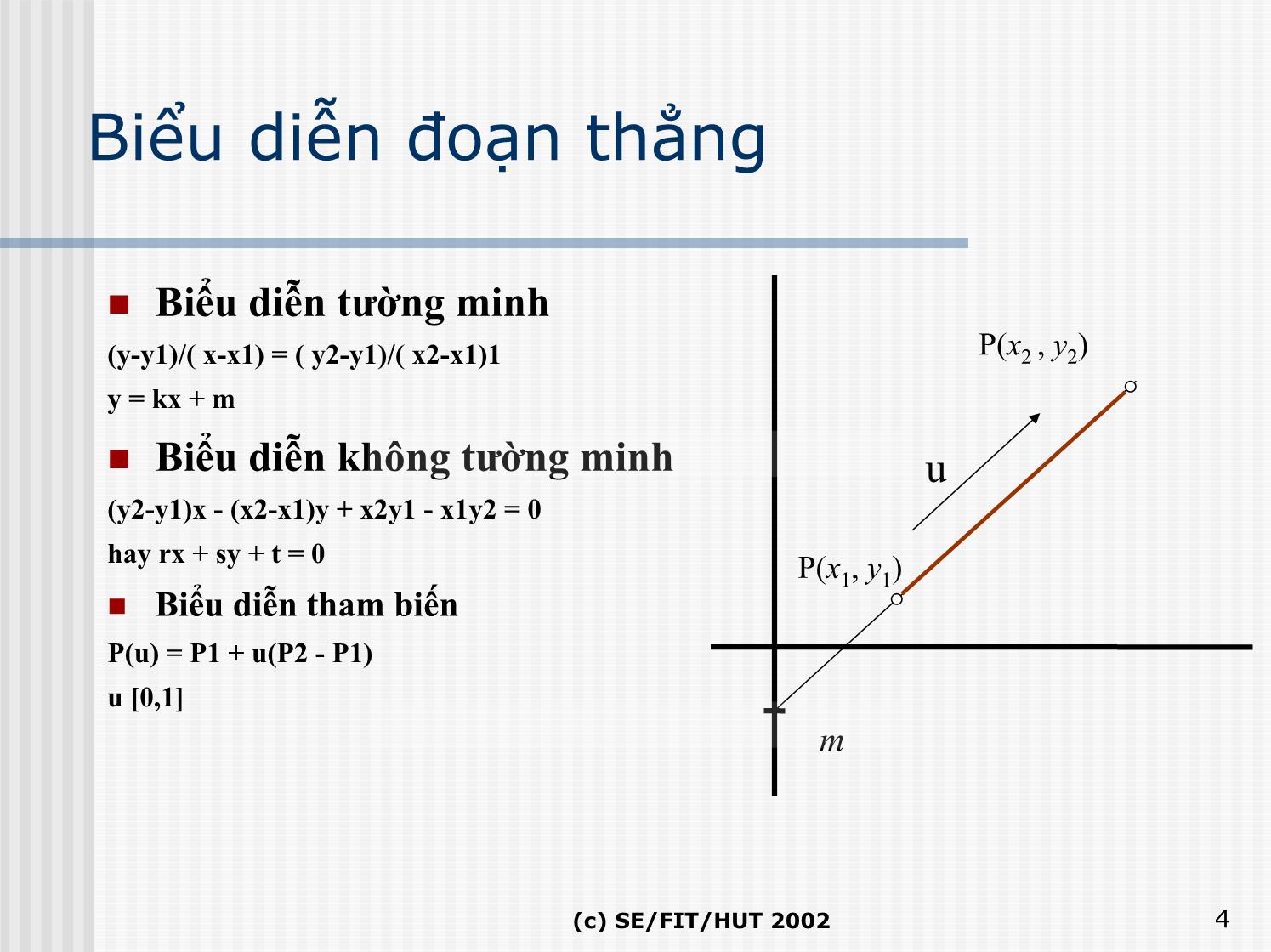
Biểudiễn đoạnthẳng
 „ Biểudiễntường minh
 (y-y1)/( x-x1) = ( y2-y1)/( x2-x1)1 P(x2 , y2)
 y = kx + m
 „ Biểudiễnkhôngtường minh u
 (y2-y1)x - (x2-x1)y + x2y1 - x1y2 = 0
 hay rx + sy + t = 0 
 P(x1, y1)
 „ Biểudiễnthambiến
 P(u) = P1 + u(P2 - P1)
 u [0,1]
 m
 (c) SE/FIT/HUT 2002 4
 ThuậttoánDDA 
 (Digital Differential Analizer)
Giảithuật thông thường
DrawLine(int x1,int y1, int x2,int y2, GiảithuậtDDA
int color) „ Với 0 < k < 1 
 x = x + 1 
{ i+1 i
 y = y + k
 float y; i+1 i
 int x; với i=1,2,3....
 for (x=x1; x<=x2; x++) 
 {
 y = y1 + (x-x1)*(y2-y1)/(x2-x1)
 WritePixel(x, Round(y), color );
 }}
 (c) SE/FIT/HUT 2002 5
 GiảithuậtBresenham
„ 1960 Bresenham thuộcIBM 
„ điểmgầnvới đường thẳng dựa
 2
 trên độ phân giai hưuhạn d1
„ loạibỏđược các phép toán d2
 chia và phép toán làm tròn 1
 như ta đãthấy trong giảithuật
 DDA 0
„ Xét đoạnthẳng với 0 < k < 1
 012
 (c) SE/FIT/HUT 2002 6
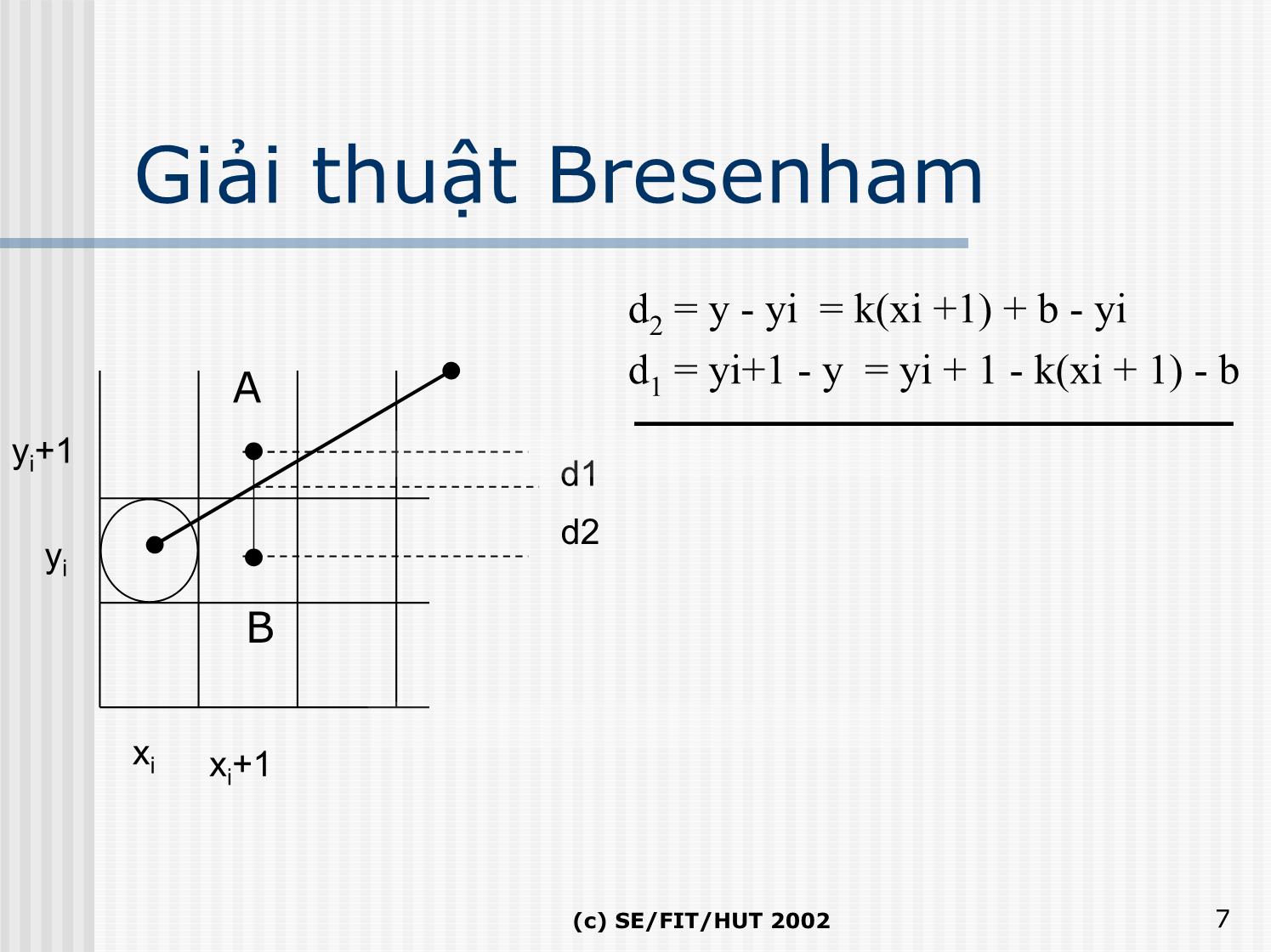
 GiảithuậtBresenham
 d2 = y - yi = k(xi +1) + b - yi
 A d1 = yi+1 - y = yi + 1 - k(xi + 1) - b
y +1
 i d1
 d2
 yi
 B
 xi
 xi+1
 (c) SE/FIT/HUT 2002 7
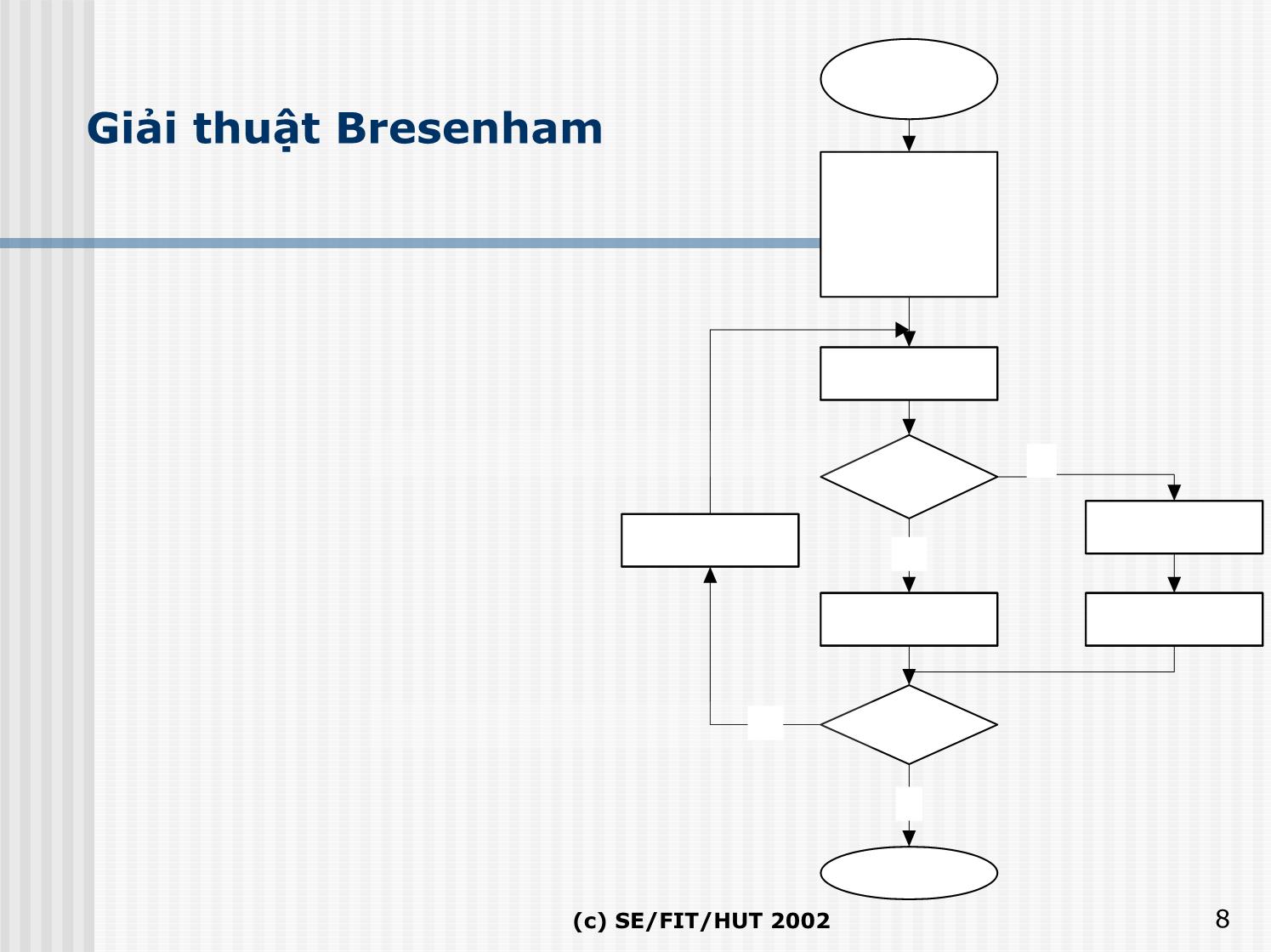
Giảithuật Bresenham
 (c) SE/FIT/HUT 2002 8
Giảithuậttrungđiểm-Midpoint 
„ Jack Bresenham 1965 / Pitteway 1967 
„ VanAken áp dụng cho việc sinh các đường
 thẳng và đường tròn 1985
„ Các công thức đơngiảnhơn, tạo đượccác
 điểmtương tự như với Bresenham
 yi+1 A
 M
„ d = F (xi + 1, yi + 1/2) là trung điểmcủa
 đoạnAB B
„
 Việc so sánh, hay kiểmtraM sẽđượcthay (xi , yi ) 
 bằng việcxétgiátrị d.
 x x
 „ Nếud > 0 điểmB đượcchọn, yi+1 = yi i i+1
 „ nếud < 0 điểmA đượcchọn. yi+1 = yi + 1
 „ Trong trường hợp d = 0 chúng ta có thể
 chọn điểmbấtkỳ hoặcA, hoặcB.
 (c) SE/FIT/HUT 2002 9
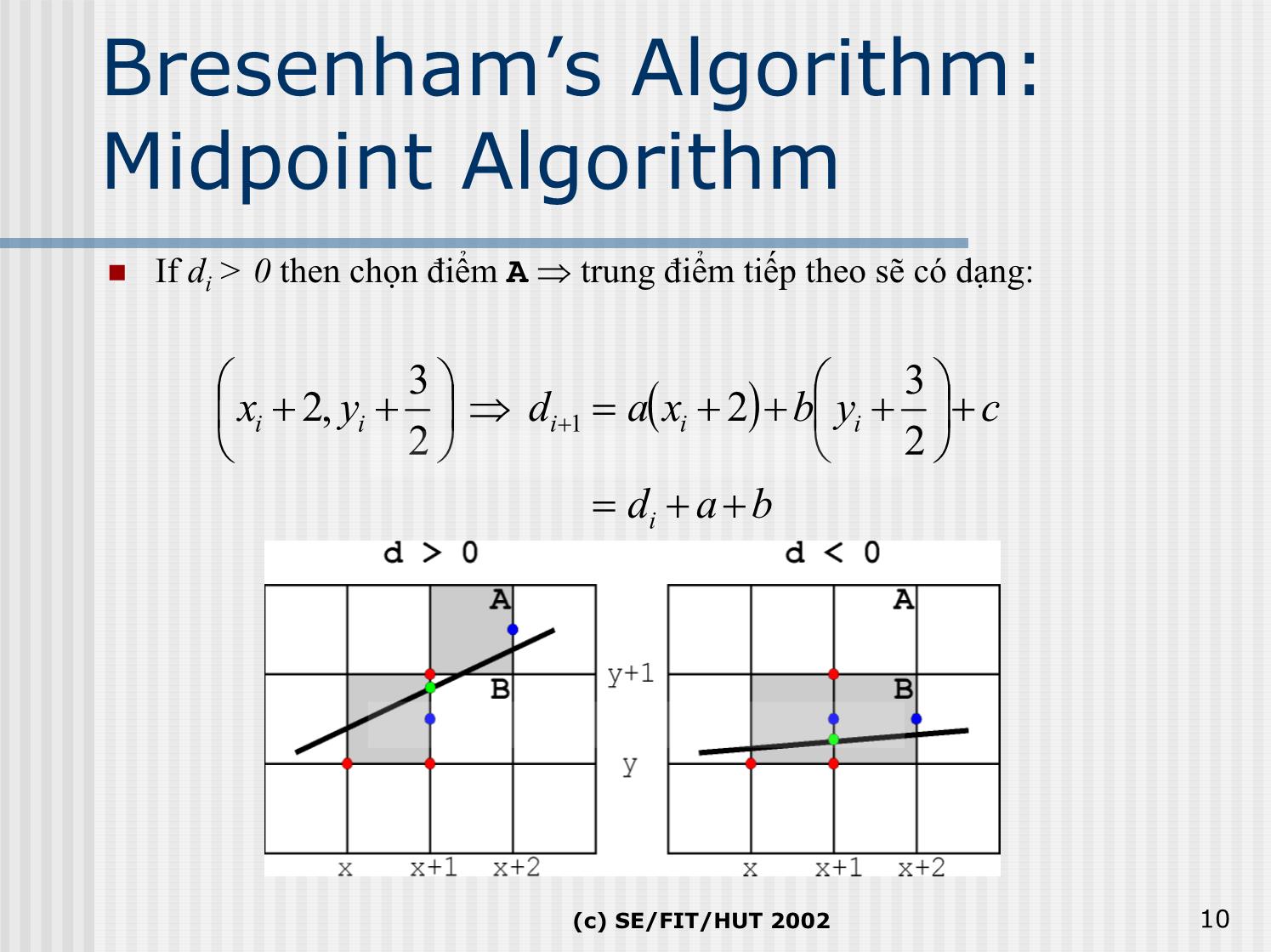
Bresenham’s Algorithm: 
Midpoint Algorithm
 „ If di > 0 then chọn điểm A ⇒ trung điểmtiếptheosẽ có dạng:
  3  3
 xi +2, yi +  ⇒ di+1 = a()xi +2 +b yi + +c
  2  2
 = di +a +b
 (c) SE/FIT/HUT 2002 10
Midpoint Line Algorithm
 dx = x_end-x_start
 dy = y_end-y_start
 d = 2*dy-dx initialisation
 x = x_start
 y = y_start
 while x < x_end 
 if d <= 0 then
 d = d+(2*dy) choose B
 x = x+1
 else
 d = d+2*(dy-dx)
 x = x+1 choose A
 y = y+1
 endif
 SetPixel(x,y)
 endwhile
 (c) SE/FIT/HUT 2002 11
Giảithuật B¾t ®Çu
 x = x1 ;
Bresenham's Midpoint y = y1;
 dx = x2 - x1;
 dy = y2 - y1;
 d = dy - dx/2;
 Putpixel (x ,y);
 No
 d <= 0
 d = d + dy - dx
 x = x + 1
 yes
 d = d + dy y = y + 1
 yes x < x2
 no
 KÕt thóc
 (c) SE/FIT/HUT 2002 12
 Sinh đường tròn
 Scan Converting Circles
 „ Explicit: y = f(x)
 yRx=±22 −
 Usually, we draw a quarter circle by 
 incrementing x from 0 to R in unit steps 
 and solving for +y for each step.
 „ Parametric:
 xR= cosθ - by stepping the angle from 0 to 90
 yR= sinθ - avoids large gaps but still insufficient.
„ Implicit: f(x) = x2+y2-R2
 If f(x,y) = 0 then it is on the circle.
 f(x,y) > 0 then it is outside the circle.
 f(x,y) < 0 then it is inside the circle.
 (c) SE/FIT/HUT 2002 13
 Midpoint Circle Algorithm
„ Sử dụng phương pháp biểudiễn không
 tường minh trong giảithuật
„ Thựchiệngiảithuậttrên1/8 đường
 tròn và lấy đốixứng xho các góc còn
 lại.
„ Với di là giá trị của đường tròn tại
 một điểmbấtkỳ ta có
 (c) SE/FIT/HUT 2002 14
Midpoint Circle Algorithm
„ As with the line, we determine the value of the decision variable by 
 substituting the mid-point of the next pixel into the implicit form of the 
 circle: 2
 2  1 2
 di = ()xi +1 + yi −  −r
  2
„ If di < 0 we choose pixel A otherwise we choose pixel B
 „ Note: we currently assume the circle is centered at the origin
 (c) SE/FIT/HUT 2002 15
Midpoint Circle Algorithm
 d = 1-r
 x = 0 initialisation
 y = r stop at diagonal ⇒ end of octant
 while y < x 
 if d < 0 then
 d = d+2*x+3
 choose
 x = x+1 A
 else
 d = d+2*(x-y)+5
 x = x+1 choose B
 y = y-1
 endif
 SetPixel(cx+x,cy+y)
 endwhile
 Translate to the circle center
 (c) SE/FIT/HUT 2002 16
 Scan Converting Ellipses
 Fxybxayab(, )=+−=22 22 22 0
„ 2a is the length of the major axis along the x axis.
„ 2b is the length of the minor axis along the y axis.
„ The midpoint can also be applied to ellipses.
„ For simplicity, we draw only the arc of the ellipse that lies 
 in the first quadrant, the other three quadrants can be drawn 
 by symmetry
 (c) SE/FIT/HUT 2002 17
 Scan Converting Ellipses: Algorithm
 A
 M tiep tuyen = -1
 B gradient
 B C
 M
 i
„ Firstly we divide the quadrant into two regions
„ Boundary between the two regions is
 „ the point at which the curve has a slope of -1
 „ the point at which the gradient vector has the i and j components of equal 
 magnitude 
 grad F(, x y )=∂Fx / ∂i +∂ F / ∂y j = 2bx22i + 2 ay j
 (c) SE/FIT/HUT 2002 18
 Ellipses: Algorithm (cont.)
 2 2
„ At the next midpoint, if a (yp-0.5)2
„ In region 1, choices are E and SE
 2 2
 „ Initial condition: dinit = b +a (-b+0.25)
 2
 „ For a move to E, dnew = dold+DeltaE with DeltaE = b (2xp+3)
 „ For a move to SE, dnew = dold+DeltaSE with 
 2 2
 DeltaSE = b (2xp+3)+a (-2yp+2)
„ In region 2, choices are S and SE
 2 2 2 2 2
 „ Initial condition: dinit = b (xp+0.5) +a ((y-1) -b )
 2
 „ For a move to S, dnew = dold+Deltas with Deltas = a (-2yp+3)
 „ For a move to SE, dnew = dold+DeltaSE with 
 2 2
 DeltaSE = b (2xp+2)+a (-2yp+3)
„ Stop in region 2 when the y value is zero. 
 (c) SE/FIT/HUT 2002 19
 Ký tự Bitmap
„ Trên cơ sỏđịnh nghĩamỗikýtự với
 một font chư cho trướclàmột
 bitmap chữ nhậtnhỏ
„ Font/typeface: set of character 
 shapes
„ fontcache
 „ các ký tự theo chuỗiliêntiếp nhau trong
 bộ nhớ
„ Dạng cơ bản ab
 „ (thường N, nghiêng I, đậm B, nghiêng
 đậmB+I) 
„ Thuộc tính
 „ Also colour, size, spacing and 
 orientation
 (c) SE/FIT/HUT 2002 20
Cấu trúc font chữ
 (c) SE/FIT/HUT 2002 21
 Ký tự vector
„ Xây dựng theo phương pháp
 định nghĩa các ký tự bởi
 đường cong mềm bao ngoài
 của chúng. 
„ Tốnkémnhấtvề mặttính
 toán
„ Chất lượngcao
 (c) SE/FIT/HUT 2002 22
 So sánh
 „ Phứctạp (Tính toán phương
„ Đơngiản trông việcsinhkýtự trình)
 ( copypixel) 
 „ Lưutrữ gọnnhẹ
„ Lưutrữ lớn
 „ Các phép biến đổidựa vào các
„ Các phép biến đổi (I,B, scale) công thứcbiến đổi
 đòi hỏilưutrữ thêm „ Kích thướcphụ thuôc vào môi
„ Kích thước không dổi trường ( ko có kích thướccố
 định)
 (c) SE/FIT/HUT 2002 23
Giải thuật đường quét sinh đa giác
Polygon Scan Conversion
„ Tồn tại rất nhiều giải thuật sinh đa giác.
„ Mỗi giải thuật phục vụ cho 1 loại đa giác nhất 
 định:
 „ some algorithms allow triangular polygons only
 „ others require that the polygons are convex and non self-
 intersecting and have no holes
 triangular convex non-convex self-intersecting religious
 (c) SE/FIT/HUT 2002 24
 Polygon Scan Conversion
„ Polygon scan conversion là giải thuật chung kinh điển cho các loại 
 khác nhau
„ Cho mỗi đoạn thẳng quét, chúng ta xác định các cạnh của đa giác cắt 
 đoạn thẳng compute spans representing the interior portions of the 
 polygons along this scan-line and fill the associated pixels.
„ This represents the heart of a scan-line rendering algorithm used in 
 many commercial products including Renderman and 3D Studio 
 MAX.
 (c) SE/FIT/HUT 2002 25
Polygon Scan Conversion
„ Dùng giảithuật (trung điểm) để xác
 định các điểmbiênchomỗi đagiác
 theo thứ tự tăng củax.
„ Các diểmphải:
 „ Không bị chia sẻ bởicácđagiáclân
 cận
 „ Các đagiácchỉ toàn các điểmcạnh( 
 điểmbiên)
„ Đảmbảo các đagiácchiasẻđiểmbiên
 mà không chia sẻ các điểm ảnh bên
 trong củamình.
 (c) SE/FIT/HUT 2002 26
 Polygon Scan Conversion
„ Thủ tục chung:
 „ Xác định giao của đường thẳng quét với cạnh đa giác
 „ Sắp xếp các giao điểm theo mức độ tăng dần của x value
 „ Điền các điểm ảnh vào giữa cặp các điểm x
„ Need to handle 4 cases to prevent pixel sharing:
 „ if intersection has fractional x value, do we round up or down?
 • if inside (on left of span) round up, if outside (on right) round down
 „ what happens if intersection is at an integer x value?
 • if on left of span assume its interior otherwise exterior
 „ how do we handle shared vertices?
 • ignore pixel associated with ymax of an edge 
 „ how do we handle horizontal edges?
 • handled as a result of previous rule (lower edges not drawn)
 (c) SE/FIT/HUT 2002 27
Polygon Scan Conversion
 integer x value is on
 right = exterior
 horizontal edge ymax not 
 removed rounded down for A included
 rounded up for B
 (c) SE/FIT/HUT 2002 28