Bài giảng Đại số tuyến tính - Chương II: Ma trận. Định thức. Hệ phương trình tuyến tính - Bài 4: Hạng ma trận - Nguyễn Hải Sơn

BÀI 4
 1
  §4: Hạng ma trận
 4.1. Định nghĩa.
 - Cho A là một ma trận cỡ mxn và một số k ≤ min{m,n}. Ma 
 trận con cấp k của A là ma trận có được từ ma trận A bằng cách bỏ 
 đi (m-k) hàng và (n-k) cột. Định thức của ma trận con cấp k của A 
 gọi là định thức con cấp k của A. 
Ví dụ: 1 2 3 4 12
 A12 
 A 2 4 6 8 
 24 2 4 
 A12 
 3 5 7 9 4 8 
 2 3 4 
 234 4 6 8 
 A123 
 2
 5 7 9 
 §4: Hạng ma trận
 -Đ/n: Hạng của ma trận A là cấp cao nhất của các 
 định thức con khác 0 có trong A. 
 Kí hiệu: rank(A) hoặc r(A)
 3
 §4: Hạng ma trận
 2
 0 0 0 0 A1 0
 O 0 0 0 0 0 0
 24 
 A13 
 0 0 0 0 0 0 
 4
 §4: Hạng ma trận
 a b c d 
 A 
 x y z t 
 5
  §4: Hạng ma trận
Ví dụ:
 a b c A có duy nhất 1 định 
 A x y z thức con cấp 3 và đó 
 là định thức con có 
 u v w cấp lớn nhất
 6
 §4: Hạng ma trận
 7
 §4: Hạng ma trận
 8
 §4: Hạng ma trận
4.2. Tính hạng của ma trận bằng biến đổi sơ cấp 
 a. Ma trận bậc thang (ma trận hình thang) là ma trận thỏa mãn 
 hai tính chất: 
 (i) Các hàng khác không nằm trên các hàng không (hàng có tất 
 cả các phần tử là 0)
 (ii) Với 2 hàng khác không, phần tử khác 0 đầu tiên của hàng 
 trên đứng trước phần tử khác 0 đầu tiên của hàng dưới. 
 Ví dụ 0 1 ... ... ... ... 
 0 0 0 2 ... ... 
 A 0 0 0 0 3 ... 
 0 0 0 0 0 0 
 0 0 0 0 0 0 
 9
 §4: Hạng ma trận
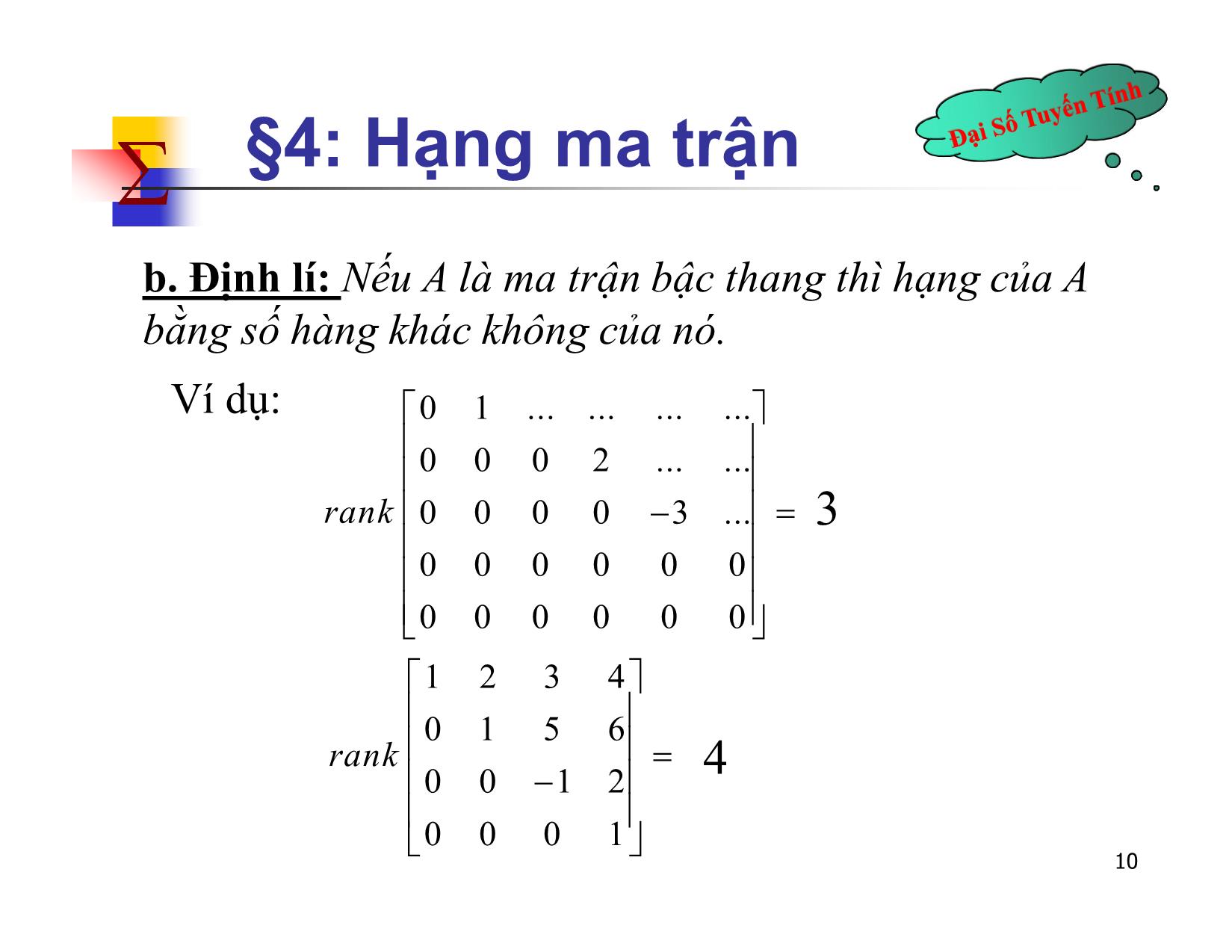
 b. Định lí: Nếu A là ma trận bậc thang thì hạng của A 
 bằng số hàng khác không của nó. 
 Ví dụ: 0 1 ... ... ... ... 
 0 0 0 2 ... ... 
 rank 0 0 0 0 3 ... 3
 0 0 0 0 0 0 
 0 0 0 0 0 0 
 1 2 3 4 
 0 1 5 6 
 rank 
 0 0 1 2 4
 0 0 0 1 
 10
 §4: Hạng ma trận
 Chứng minh định lí:
 a a... a ... a
 11 12 1r 1 n a11 a 12.. a 1r 
 0a ... a ... a 0a .. a 
 22 2r 2 n A12..r 22 2r 
 .. .. ... .. ... .. 12..r .. .. .. .. 
 a a 
A 0 0 ...r r ... r n 0 0 .. arr 
 0 0 ... 0 ... 0 
 Các MT con cấp > r 
 ... ... ... ... ... ... chứa ít nhất 1 hàng = 0
 0 0 ... 0 ... 0 
 11
 §4: Hạng ma trận
 “Sử dụng các phép biến 
 Chú ý: đổi sơ cấp trên ma trận”
 A B (ma trận bậc thang)
 ?
 Vấn đề: r(A) = r(B)
 12
 §4: Hạng ma trận
Chú ý:
Định lý: Các phép biến đổi sơ cấp không làm 
 thay đổi hạng của ma trận.
 13
 §4: Hạng ma trận
 “biến đổi 
 sơ cấp
 A B (ma trận bậc thang)
 r(A) = r(B)
 14
 §4: Hạng ma trận
 15
 §4: Hạng ma trận
 Ví dụ: Tìm hạng ma trận:
 1 3 2 0 1 4 
 0 3 3 4 0 1 
 A 0 0 5 8 9 1 r( A ) 3
 0 0 0 0 0 0 
 0 0 0 0 0 0 
 16
 §4: Hạng ma trận
  Ví dụ: Tìm hạng của ma trận:
 1 1 2 0 
 2 1 1 3 
 A 
 4 5 2 1 
 1 7 3 2 
 17
 §4: Hạng ma trận
  Lời giải.
 1 1 2 0 1 1 2 0 
 2 1 1 3 0 -1 -5 3 
A  h2 ( 2) h 1 
 h 4 h
 4 5 2 1 3 1 
 h 1 h 0 9 10 -1
 4 1 
 1 7 3 2 0 8 5 2 
 18
 §4: Hạng ma trận
 1 1 2 0 1 1 2 0 
 2 1 1 3 0 1 5 3 
  h2 ( 2) h 1 
 h3 4 h 1
 4 5 2 1 h 1 h 0 9 10 1 
 4 1 
 1 7 3 2 0 8 5 2 
 1 1 2 0 1 1 2 0 
 h 9 h 
 3 2 0 1 5 3 0 1 5 3
   h4 ( 1) h 3 
 h4 8 h 2 0 0 -35 26 0 0 35 26 
 0 0 -35 26 0 0 0 0 
 r(A) 3
 19
 §4: Hạng ma trận
 Ví dụ: Biện luận theo m hạng của ma trận 
 sau:
 1 5 6 m 0 r(A) = 2
 A 0 4 7 m 0 r(A) = 3
 0 0 m0 
 20
 §4: Hạng ma trận
  Ví dụ: Biện luận theo m hạng của ma trận 
 sau: 1 9 0 7 
 0 2 4 8 
 B 
 0 0 (m20 1) ( m0 1) 
 0 0 0 0 
 m 1 r( A ) 2
 m 1 r( A ) 3
 m 1 r( A ) 3
 21
 §4: Hạng ma trận
 Bài tập: Biện luận theo m hạng của ma trận 
 sau:
 1 2 2 1 2 2 
 h2 h 3
 c c 
 A 2 m 1 2 3
  1 5 4 
 1 4 5 2 1 m 
 22
 §4: Hạng ma trận
 1 2 2 
 ... 0 3 6 
 0 0 3m 42 
 3m 42 0 m 14 r(A) = 2
 3m 42 0 m 14 r(A) = 3
 23
 §4: Hạng ma trận
 Bài tập: Biện luận theo a, b hạng của ma 
 trận sau:
 1 2 0 1 
 2 1 3 0 
 A 
 0 3 a b 
 3 3 3 1 
 24