Bài giảng Đại số tuyến tính - Chương II: Ma trận. Định thức. Hệ phương trình tuyến tính - Bài 2: Định thức - Nguyễn Hải Sơn

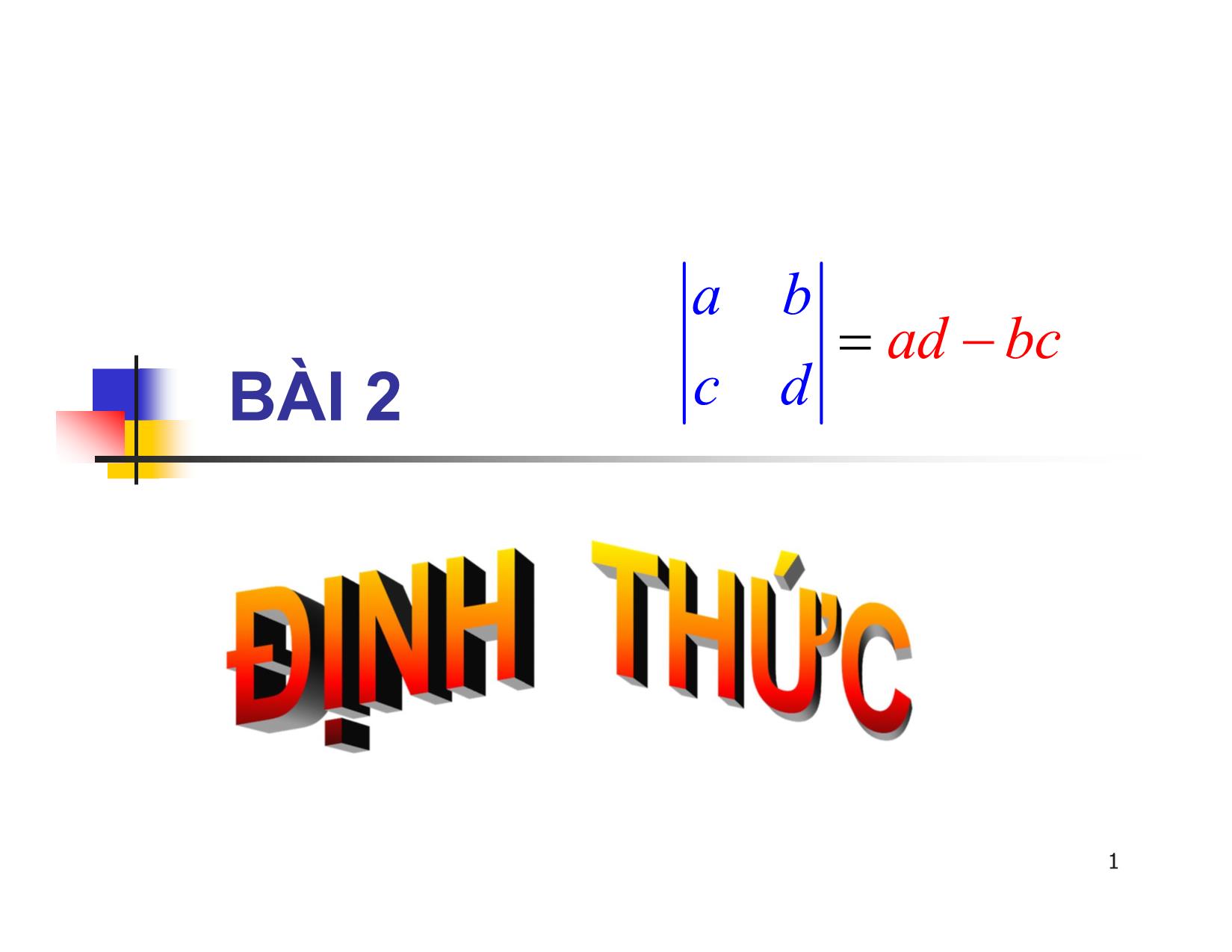
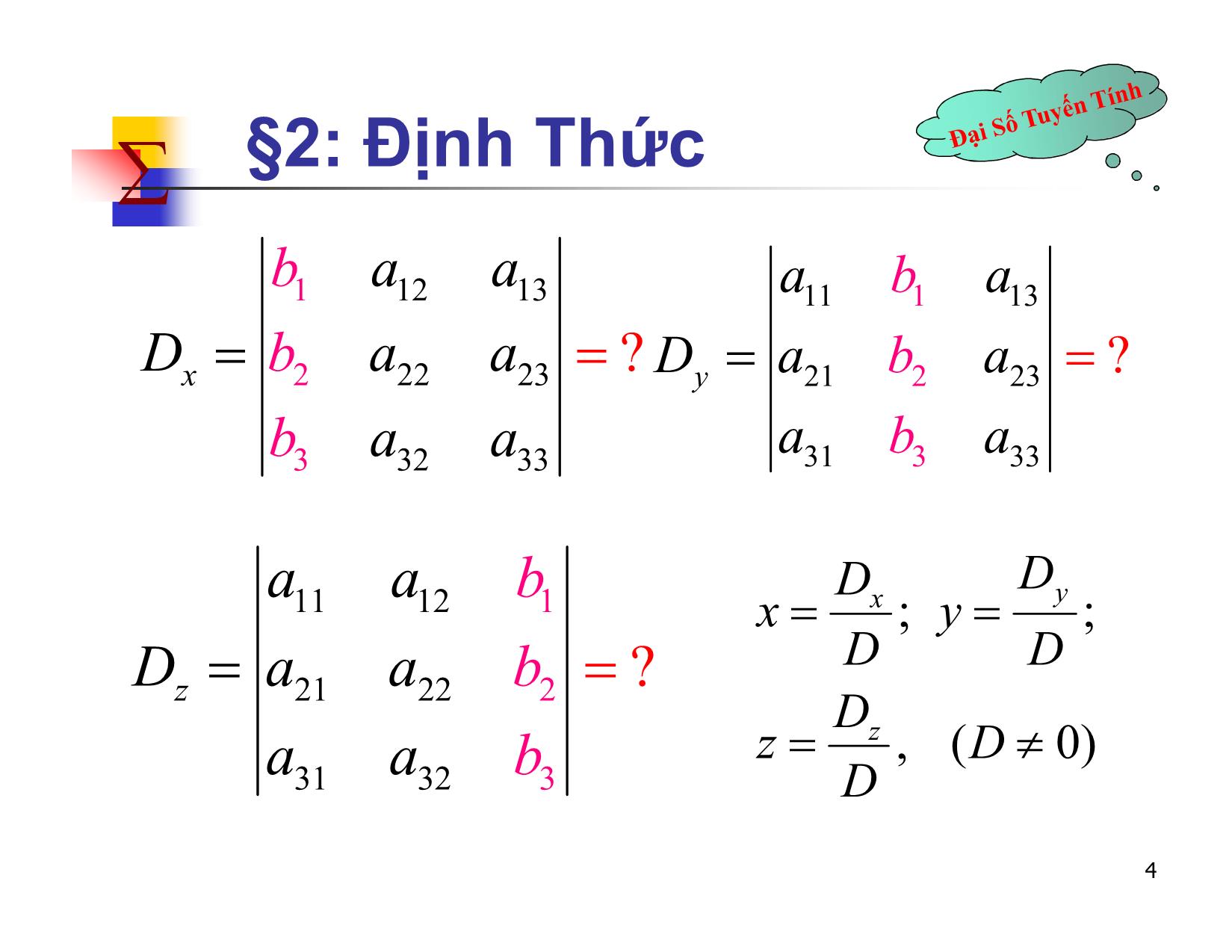
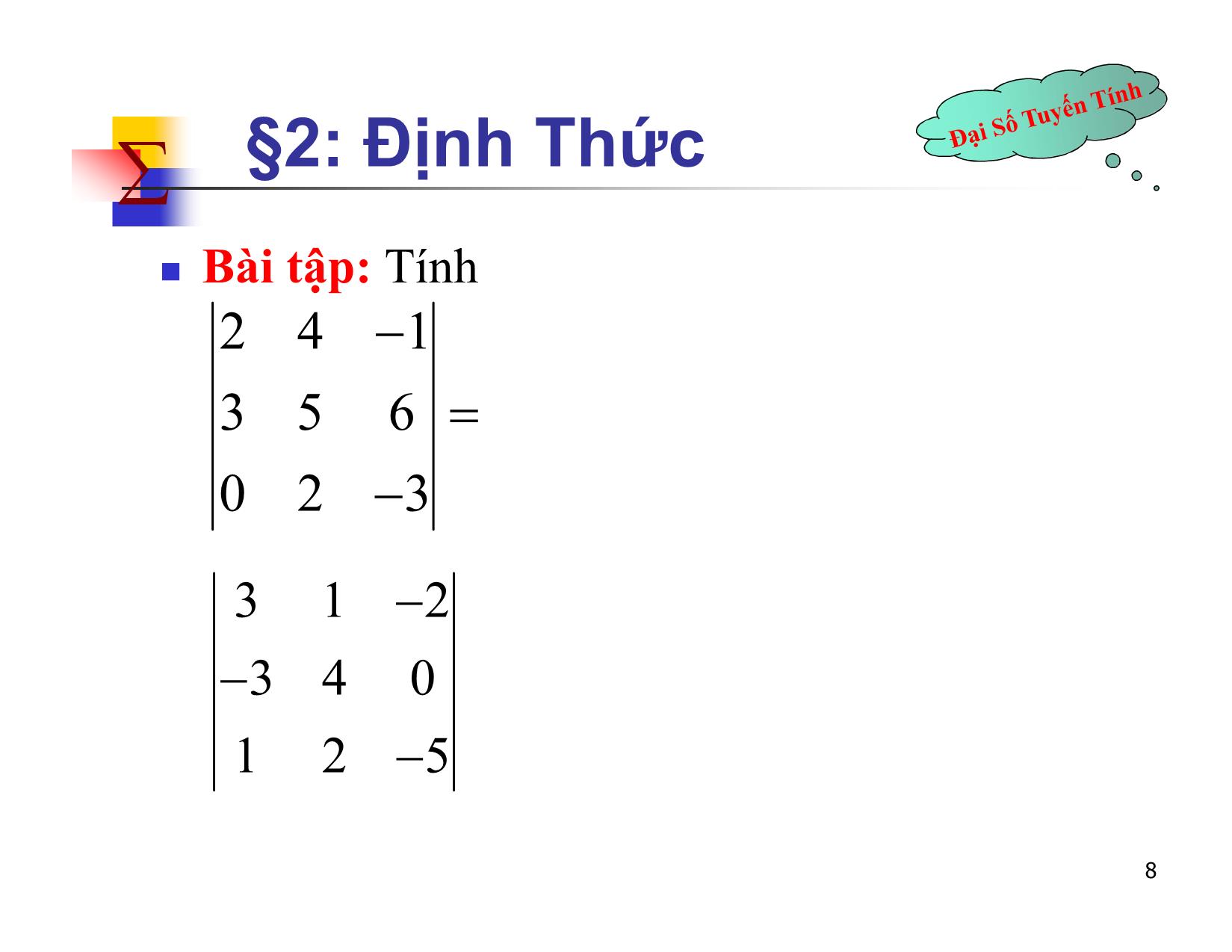
 a b
 ad b c
BÀI 2 c d
 1
 §2: Định Thức
 2.1 Mở đầu
 ax by c
- Xét hệ phương trình sau: 
 a''' x b y c
 Theo phương pháp Grame ta có công thức 
 nghiệm sau:
 D D “Định thức” cấp 2
 x x ; y y ,( D 0)
 DD
 a b c b a c
 D ;;'' D D ac a c
 a'''''' bx c b y a c
 2
 §2: Định Thức
 Xét hệ phương trình sau:
 a11 x a 12 y a 13 z b1
 a21 x a 22 y a 23 z b2
 a31x a 32 y a 33 z b3
 a11 a 12 a 13
Ta có thể định nghĩa: D a21 a 22 a 23 ?
 a31 a 32 a 33
 3
 §2: Định Thức
 b1 a12 a 13 a11b1 a 13
 Dx b2 a22 a 23 ? Dy a21b2 a 23 ?
 b3 a32a 3 3 a31b3 a 33
 a a b D Dy
 11 12 1 x x ;; y 
D a a b ? DD
 z 21 22 2 D
 z z , ( D 0)
 a31 a3 2 b3 D
 4
 §2: Định Thức
 Định thức cấp 2:
 a11 a 12
 D2 a 11 a 22 a 12 a 21.
 a21 a 22
  Ví dụ:
 2 3
 2.6 5.3 3.
 5 6
 5
  §2: Định Thức
  Định thức cấp 3: (Quy tắc hình sao)
 a11 a 12 a 13
 ()a a a a a a a a a
D3 a 21 a 22 a 23 11 22 33 31 12 23 13 32 21
 ()a13 a 22 a 31 a 33 a 21 a 12 a 11 a 32 a 23
 a31 a 32 a 33
 6
 §2: Định Thức
 Ví dụ: Tính
 2 1 5
 1 4 0
 3 6 2
 7
 §2: Định Thức
  Bài tập: Tính
 2 4 1
 3 5 6 
 0 2 3
 3 1 2
 3 4 0
 1 2 5
 8
 §2: Định Thức
  Bài tập: Tính
 3 1 4
 5 2 0
 6 1 7
 9
 §2: Định Thức
2.2 Định nghĩa
2.2.1 Đ/n1: Cho ma trận A=[aij ] vuông cấp n. Phần phụ 
 đại số của aij, kí hiệu là Aij , được xác định như sau
 i j
 Aij ( 1) det M ij
 trong đó Mij là ma trận có được từ ma trận A bằng cách 
 bỏ đi hàng i, cột j. 
 10
 §2: Định Thức
 Ví dụ: Cho ma trận
 1 4 3 
 A 5 2 1 
 3 6 0 
 1 1
 AM11 ( 1) det( 11 ) 6
 1 2 3 5 1
 A12 ( 1) det(M12 ) ( 1) 3
 3 0
 5 2
 AM ( 1)1 3 det( ) ( 1)4 36
 13 13 3 6
 11
 §2: Định Thức
  Bài tập: Với 1 4 3 
 A 5 2 1 
 3 6 0 
 Tính
 A21 
 A23 
 A33 
 12
 §2: Định Thức
2.2.2 Đ/n 2.
Cho ma trận vuông cấp n A [] aij
Định thức của A là một số được kí hiệu là detA, 
hay 
 a11 a 12... a 1n
 a a... a
 A 21 22 2n
 ... ... ... ...
 an1 a n 2 ... a nn
được xác định quy nạp theo n như sau:
 Nếu n=1 thì |[a11 ]| = a11.
 13
 §2: Định Thức
 Nếu n=1 thì |[a11 ]| = a11.
 Nếu n>1 thì 
 a11 a 12 a 1n 
A A a11 A 11 a 12 A 12  a 1n A 1 n
 * 
(khai triển theo hàng 1)
 - Định thức của ma trận vuông cấp n gọi là 
 định thức cấp n.
 14
 §2: Định Thức
 Ví dụ: Tính định thức sau: 1 4 3
 5 2 1
 3 6 0
 15
 §2: Định Thức
 2.3. TÝnh chÊt cña ®Þnh thøc
(i) detAt = detA.
Hq : Một mệnh đề về định thức nếu đã đúng cho 
 hàng thì cũng đúng với cột và ngược lại.
 Do đó, trong các tính chất sau đây ta chỉ phát 
 biểu cho “hàng”.
 VÝ dô: 1 4 7 1 2 3
 2 5 8 4 5 6
 3 6 9 7 8 9
 16
 §2: Định Thức
 (ii) Nếu đổi chỗ hai hàng bất kì của định thức 
 thì định thức đổi dấu
  VÝ dô:
 a b c x y z
 h1 h 3
 * ** * **.
 x y z a b c
 17
 §2: Định Thức
Hq. Khi tính định thức ta có thể khai triển theo 
 hàng và cột bất kì. 
 2 2 1 0
 j 4
 3 1 2 1
 a14AAAA14 a 24 24 a 34 34 a 44 44
 0 4 3 0
 5 0 4 2
 2 2 1 2 2 1
 6 8
 0.AA14 1 (1)04 3 0 . 34 ( 2) (1)31286 
 5 0 4 0 4 3
 18
 §2: Định Thức
  Ví dụ: Tính định thức sau:
 2 3 0 1 2 0
 i 4
 ( 1)(1) 5 1 5 1 6 (1)4 7 11
 2 2 3 0 2 3
 (24 5) 6( 3 26)
 19 174 193
 19
 §2: Định Thức
 Bµi TËp: TÝnh ®Þnh thøc sau
 1 2 3 1
 0 2 4 2
 1 3 0 4
 2 0 1 5
 20
 §2: Định Thức
(iii) Nếu các phần tử của một hàng nào đó của 
 định thức có dạng tổng của 2 số hạng thì ta có 
 thể viết định thức thành tổng của 2 định thức 
 như sau: 
 ... ... ... ... ... ... ... ... ... ... ... ...
 a b a b ...a b a a ...a b b ...b
 1122 nn12 n12 n
 ... ... ... ... ... ... ... ... ... ... ... ...
 ... ... ... ... ... ... ... ... ... ... ... ...
 (các phần tử còn lại giữ nguyên)
 21
 §2: Định Thức
  VÝ dô:
 2 3 2 3 2 3
 a b c d a c b d
 22
  §2: Định Thức
 (iv) Nếu nhân một hàng nào đó của định thức với một 
 số λ thì được định thức mới bằng λ lần định thức cũ. 
Hq: (1) Nếu các phần tử của một hàng có thừa số chung 
 thì ta có thể đưa thừa số đó ra ngoài dấu định thức.
  VÝ dô: 2 5 4 10 
 AA ; 2 
 3 4 6 8 
 410 2.2 2.5 2 5 2 5
 det(2)AA 2 2.2 2det().2
 6 8 6 8 2.3 2.4 3 4
 23
 §2: Định Thức
 VÝ dô:
 1 2 3 1 2 3 
 h1 h 3 
 ABA 5 7 9  5 7 9 
 1 2 3 1 2 3 
 det(ABAAA ) det( ) det( ) det( ) det( ).
 24
 §2: Định Thức
 (v) Nếu thêm vào một hàng của định thức bội λ của 
 hàng khác thì định thức không đổi. 
  VÝ dô:
 1 2 3 1 2 3
 h2 ( 4) h 1
 4 5 6 0 3 6
 a b c a b c
 25
  §2: Định Thức
(vi)
  Ví dụ:
 2 0 0 0
 3 0 0
 0 3 0 0 i 1
 a A 2 0 5 0
 0 0 5 0 11 11
 0 0 1
 0 0 0 1
 i 1 5 0
 2. ( 3) 2.( 3).5.1
 0 1 26
 §2: Định Thức
  Ví dụ:
 1 5 8 2
 0 3 6 0
 0 0 2 9 1.3.2.5 30
 0 0 0 5
 27
  §2: Định Thức
(vii) Cho A, B là các ma trận vuông cấp n. Khi đó
 det(AB) = detA.detB 
 28
 §2: Định Thức
 Ví dụ: Cho 2 ma trận
 2 3 1 5 8 31 
 AB ; AB 
 1 4 2 7 9 33 
 det(AB ) 5;det( ) 3
 det(AB ) 15 5.( 3) det( A ).det( B )
 29
 §2: Định Thức
2.4 Tính định thức bằng biến đổi sơ cấp 
 30
 §2: Định Thức
 Ví dụ 1: Tính định thức
 1 2 1 3 1 2 1 3
 2 3 1 5 h2 2 h 1 0 1 3 1
 D 
 1 6 5 2 1 6 5 2
 3 4 2 7 3 4 2 7
 1 2 2 1 1 3 3
 h h 1 3 1
 3 1 j 1
 0 1 3 3 1 1
 h 3 h a11 A11 1. 8 4 1
 4 1 0 8 8 4 4 1
 2 1 2
 03 4 2 1 2 7 2
 31
 §2: Định Thức
 Ví dụ 2: Tính định thức
 0 2 3 5 1 0 2 2
 1 0 2 2 h1 h 2 0 2 3 5
 D 
 2 3 0 6 2 3 0 6
 4 1 7 0 4 1 7 0
 1 0 2 2
 2 3 5
 h3 2 h 1 0 2 3 5
 1 3 4 2
h 4 h 0 3 4 2
 4 1 1 1 8
 0 1 1 8
 32
 §2: Định Thức
 Bài tập: Tính định thức sau
 1 1 2 0
 3 1 0 4
 D 
 2 0 5 2
 0 3 6 1
 33
 §2: Định Thức
 Ví dụ 3: Tính định thức cấp n sau
 1 1 1 ... 1 1 1 1 ... 1
 1 0 1 ... 1
 h2 h 1 0 1 ... 0
 Dn 1 1 0 ... 1 1 1 0 ... 1
 ... ... ... ... ... ... ... ... ... ...
 1 1 1 ... 0 1 1 1 ... 0
  Tiếp tục hàng 3 trừ hàng 1, hàng 4 trừ 
 hàng 1, 
 34
 §2: Định Thức
 Ta được:
 1 1 1 ... 1
 0 1 0 ... 0
 n 1
 Dn 0 0 1 ... 0 ( 1)
 ... ... ... ... ...
 0 0 0 ... 1
 35