Bài giảng Đại số tuyến tính - Chương II: Ma trận. Định thức. Hệ phương trình tuyến tính - Bài 1: Ma trận - Nguyễn Hải Sơn

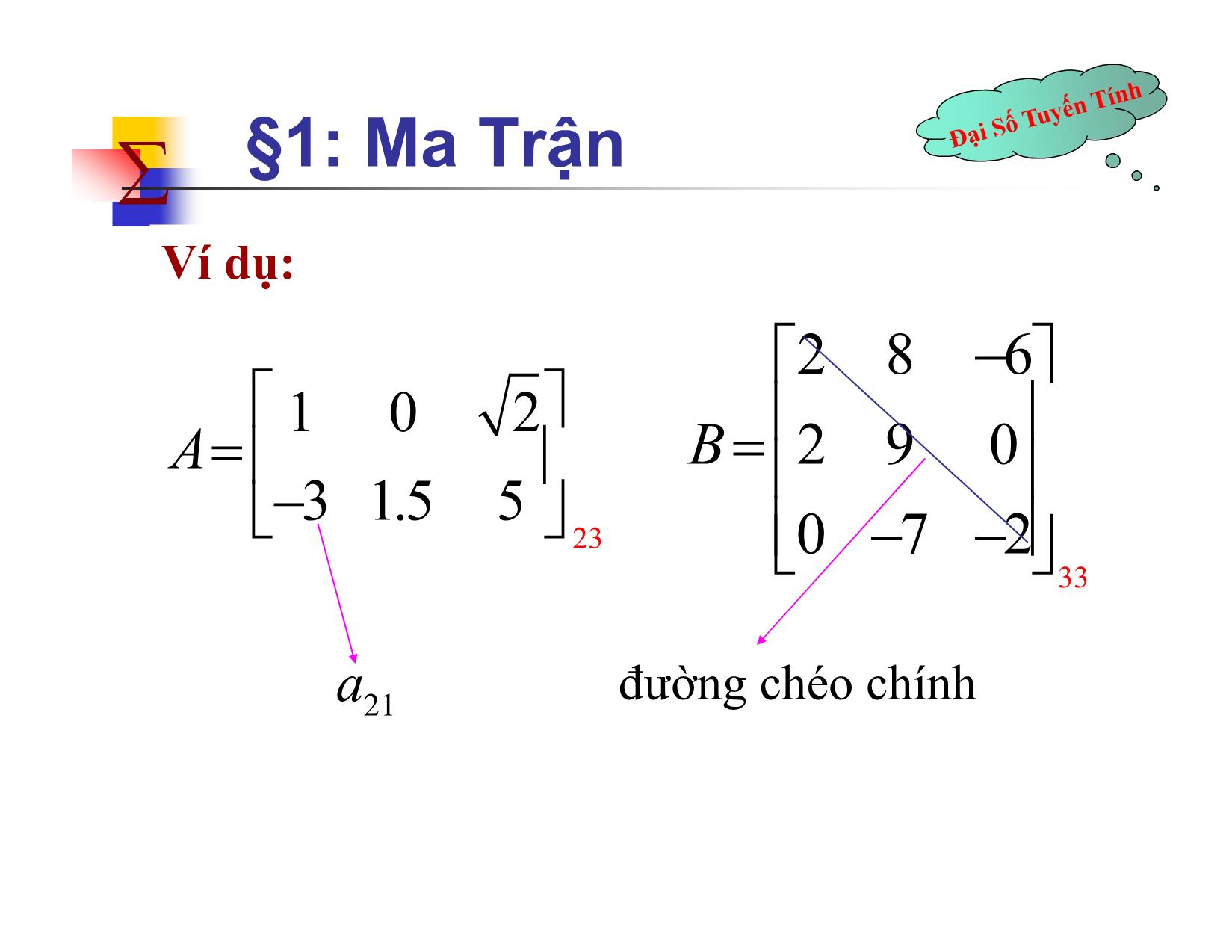
  CHƯƠNG II:
 MA TRẬN-ĐỊNH THỨC
 -HỆ PHƯƠNG TRÌNH TUYẾN TÍNH
I. MA TRẬN
II. ĐỊNH THỨC
III. HẠNG MA TRẬN-MA TRẬN NGHỊCH ĐẢO
IV. HỆ PHƯƠNG TRÌNH TUYẾN TÍNH
   
  
   
BÀI 1 
 §1: Ma Trận
 1.1 Các khái niệm
 a) Định nghĩa: Ma trận là một bảng gồm m.n 
 số thực (phức) được viết thành m hàng và n cột 
 như sau: 
 a11 a 12... a 1n 
 a a... a 
 21 22 2n 
 ... ... ... ... 
 am1 a m 2 ... a mn 
 Ký hiệu: A = [aij]mn
 §1: Ma Trận
 Hàng thứ nhất
 a11 a 12... a 1j ... a 1 n 
 a a... a ... a 
 21 22 2j 2 n 
 ... ... ... ... ... ... 
 Hàng thứ i
 ai1 a i 2 ... a ij ... a in 
 ... ... ... ... ... ... 
 mn: gọi là cấp của ma trận
 am1 a m 2 ... a mj ... a mn 
 aij: Phần tử nằm ở hàng i cột j
 Cột thứ 2 Cột thứ j
 §1: Ma Trận
 Ví dụ:
 2 8 6 
 1 0 2 
 A B 2 9 0
 3 1.5 5 
 23 0 7 2 
 33
 a21 đường chéo chính
 §1: Ma Trận
 b) Các ma trận đặc biệt.
 1. Ma trận không:a ij 0,  i , j .
 (tất cả các phần tử đều = 0)
 Ví dụ:
 0 0 0 
 O 
 0 0 0 
 §1: Ma Trận
 2. Ma trận vuông: m = n. (số hàng = số cột)
 Đ/n: Ma trận vuông n hàng, n cột được gọi là ma trận 
 vuông cấp n.
 Ma trận vuông cấp 3
 Ví dụ:
 0 7 8 
 1 3 
 ; 4 2 0 
 2 7 
 5 0 2 
Ma trận vuông cấp 2
 §1: Ma Trận
 A [] a a
 Cho ma trận vuông cấp n ij . Các phân tử ii gọi 
 là các phần tử chéo. Đường thẳng qua các phần tử 
 chéo gọi là đường chéo chính. 
 Ví dụ: 2 8 6 
 B 2 9 0 
 0 7 2 
 33
 đường chéo chính
 §1: Ma Trận
 3. Ma trận chéo: là ma trận vuông có:
 aij 0,  i j .
 (các phần tử ngoài đường chéo chính = 0)
 Ví dụ:
 a11 0 ... 0 
 2 0 0 0a ... 0 
 22 
 0 4 0 ... ... ... ... 
 0 0 9 
 0 0 ... ann 
 §1: Ma Trận
 4. Ma trận đơn vị: là ma trận chéo có:
 aii 1,  i 1,2,..., n .
 Ký hiệu: E, En ( hoặc I, In).
 Ví dụ:
 1 0 ... 0 
 1 0 0 
 1 0 0 1 ... 0
 EEE , 0 1 0 , 
 2 3 n
 01 ......... 
 0 0 1 
 0 0 ... 1 
 §1: Ma Trận
 5. Ma trận tam giác: là ma trận vuông có
 aij 0,  i j . (tam giác trên)
 aij 0,  i j . (tam giác dưới)
 Ví dụ:
 1 2 5 4 2 0 0 0 
 7 1 0 0 
 0 3 1 0 
 0 0 2 6 0 8 2 0 
 0 0 0 9 2 9 1 5 
 MT tam giác trên MT tam giác dưới
 §1: Ma Trận
 6. Ma trận cột:là ma trận có n=1.
 Ma trận cột có dạng: a11 
 a 
 21 
 : ai 
 .. m
 am1 
 7. Ma trận hàng: là ma trận có m=1.
 Ma trận hàng có dạng: a11 a 12 ... a 1n 
 §1: Ma Trận
 8. Ma trận chuyển vị: cho ma trận A=[aij]mn, 
 ma trận chuyển vị của ma trận A ký hiệu: 
 T T
 A và xác định A =[bij]nm với bij=aji với 
 mọi i,j. 
 (chuyển hàng thành cột, cột thành hàng )
 Ví dụ:
 1 6 
 1 2 5 T 
 AA 2 7 
 6 7 9 
 5 9 
 NX: ()AATT 
 §1: Ma Trận
 1.2. Ma trận bằng nhau:
 A a b B a b,,.  i j
 ij m n ij m n ij ij
 VD
 a 1
 a 1 2 1 1 y b 3
 9 b 0 x 3 0 x 9
 y 2
 Chú ý: Chỉ xét 2 ma trận bằng nhau nếu chúng 
 cùng cỡ. 
 §1: Ma Trận
 1.3. Các phép toán trên ma trận:
 a. Phép cộng hai ma trận: (cùng cỡ)
 a b a b 
 ij mn ij mn ij ij mn
 (cộng theo từng vị trí tương ứng)
 Ví dụ:
 11 2 03 
 -1 1 
 3 5 2 4 
 4 2 1 5 5 3 
 §1: Ma Trận
 Bài tập: Tính
 2 3 3 3 4 2 7 -1 
 11 8 
 1 4 6 1 7 2 
 4 2 0 6 3 2 -2 1 
 §1: Ma Trận
 Các tính chất: Giả sử A,B,C, θ là các ma 
 trận cùng cấp, khi đó:
 i) A B B A
 ii) A  A
 iii)()() A B C A B C
 §1: Ma Trận 
 1.3. Các phép toán trên ma trận:
 b. Phép nhân một số với một ma trận:
  a ., a  
 ij mn ij mn
 (các phần tử của ma trận đều được nhân cho  )
 Ví dụ:
 3 2 0 0 
 2 7 4 5 14 8 10 
 0 2 1 0 -4 2 
 §1: Ma Trận 
 Bài tập: Tính
 2 3 -9 
 3 4 0 12 
 5 1 -3 
 §1: Ma Trận 
 Các tính chất:  ,,,  RAB  là hai ma trận 
 cùng cấp, khi đó 
 i) ( A B ) A B
 ii) (  ) A A  A
 iii) (  A ) (  ) A
 iv) 1 A A
 §1: Ma Trận
 Chú ý: ABAB ( 1)
 Nhận xét: trừ 2 ma trận là trừ theo vị trí tương ứng
 1 3 6 5 5 2 
 4 5 1 3 3 2 
 §1: Ma Trận
 Bài tập: Tính
 2 4 1 3 
 2 
 3 7 2 4 
 §1: Ma Trận 
 1.3 Các phép toán trên ma trận:
 c. Phép nhân hai ma trận: Cho hai ma trận AB mp ;, pn 
 Khi đó ma trận A mp B pn [] c ij mn gọi là tích của 
 hai ma trận A, B. Trong đó: 
 cababij i1 1 j i 2 2 j ... ab ip pj ,  i 1, mj ; 1, n .
 ai1 ai2 aip Hàng thứ i của ma trận A.
 Cột thứ j của ma trận B.
 b1 j b2 j bpj
Như vậy c i j = hàng thứ i của ma trận A nhân tương ứng 
với cột thứ j của ma trận B rồi cộng lại.
 §1: Ma Trận 
 Ví dụ: Nhân hai ma trận sau:
 3 2 1 1 2 
 0 1 4 3 0 
 2 3 0 4 1 
 33 32 32
 §1: Ma Trận
 Ví dụ: Tính
 2 4 1 
 1 4 2 
 2 3 0 
 1 0 4 
 3 5 1 
 §1: Ma Trận
 Bài tập: Tính
 1 2 3 3 1 
 0 4 2 2 0 
 5 1 1 6 3 
 §1: Ma Trận
 Chú ý:
 - Muốn nhân A với B thì số cột của A = số hàng của B. 
 Do đó, việc tồn tại AB không suy ra được việc tồn tại BA. 
 -Nói chung AB BA
 Ví dụ:
 3 3 3 6 
 1 2  11  1 2 
 4 4 4 8 
 1 4 3 1 19 1 3 1 1 4 2 10 
 5 2 4 0 23 5 4 0 5 2 4 16 
 §1: Ma Trận
 Các tính chất: Ta giả sử các ma trận có cấp 
 phù hợp để tồn tại ma trận tích
 i)()() A BC AB C
 ii)() A B C AB AC
 iii)() A B C AC BC
 iv) AE EA A ( E là MT đơn vị)
 §1: Ma Trận
  Ví dụ:
 1 5 7 1 0 0 1 5 7 
 AE 8 4 2 0 1 0 8 4 2 A
 3 1 0 0 0 1 3 1 0 
 1 0 0 1 5 7 1 5 7 
 EA 0 1 0 8 4 2 8 4 2 A
 0 0 1 3 1 0 3 1 0 
 §1: Ma Trận
*Chú ý:
 - Nếu A, B là các ma trân vuông cấp n thì AB và BA 
 tồn tại và cũng là ma trận vuông cấp n. 
 - Kí hiệu: Am = A.AA (m ma trận A) 
 - Đa thức của ma trận:
 n n 1
 Cho đa thức Pn()... x a0 x a 1 x a n
 và ma trận vuông A [] aij n
 Khi đó: 
 n n 1
 Pn( A ) a0 A a 1 A ... a n E n
 §1: Ma Trận
 2
 Bài tập: Cho f( x ) x 3 x 4
 1 2 3 
và ma trận A 0 3 4 
 0 0 2 
Tính f(A) =?
 §1: Ma Trận
 2
 f( A ) A 3 A 4 I3
 123123 123 100 
 034034 3034 4010 
 002002 002 001 
 0 14 26 
 0 14 32 
 0 0 6 
 §1: Ma Trận
1.4 Các phép biến đổi sơ cấp trên ma trận:
1. Nhân một số khác không với một hàng (cột) 
 của ma trận. Ký hiệu: AB hi (  c i )
2. Đổi chỗ hai hàng (cột) của ma trận. Ký 
 hiệu: AB hi h j ( c i  c j )
3. Cộng vào một hàng (cột) với một hàng (cột) 
 khác đã nhân thêm một số khác không. Ký 
 h  h ( c  c )
 hiệu: AB i j i j
 §1: Ma Trận
  Ví dụ: Đưa ma trận sau về dạng ma trận hình 
 thang.
 1 1 2 0 
 2 1 1 3 
 4 5 2 1 
 1 7 3 2 
 §1: Ma Trận
 1 1 2 0 1 1 2 0 
 2 1 1 3 0 1 5 3 
  h2 ( 2) h 1 
 h3 4 h 1
 4 5 2 1 h 1 h 0 9 10 1 
 4 1 
 1 7 3 2 0 8 5 2 
 1 1 2 0 1 1 2 0 
 h 9 h 
 3 2 0 1 5 3 0 1 5 3
   h4 ( 1) h 3 
 h4 8 h 2 0 0 -35 26 0 0 35 26 
 0 0 -35 26 0 0 0 0 
 §1: Ma Trận
 Ví dụ: Đưa ma trận sau về dạng ma trận hình 
 thang:
 0 2 1 
 2 1 3 
 3 0 5 
 §1: Ma Trận
 Bài tập: Đưa ma trận sau về dạng ma trận hình 
 thang:
 1 2 1 0 
 2 3 0 5 
 4 1 2 0 
 3 0 5 7 
  MỘT SỐ ĐỀ THI
 2 1 2
Câu 1. Cho ma trận A và đa thức f ( x ) 3 x 5 x 1
 5 3 
Tính f () A . Tìm ma trận X thỏa mãn (5AAXA2 3 ) t
 (Đề 1- K55)
 1 3 2
Câu 2. Cho ma trận A và đa thức f ( x ) x 8 x 1
 2 7 
Tính f () A . Tìm ma trận Y thỏa mãn YAAA(82 3 ) t
 (Đề 2- K55)
 38