Bài giảng Cơ sở truyền số liệu - Chương 3: Định tuyến động (Dynamic routing)
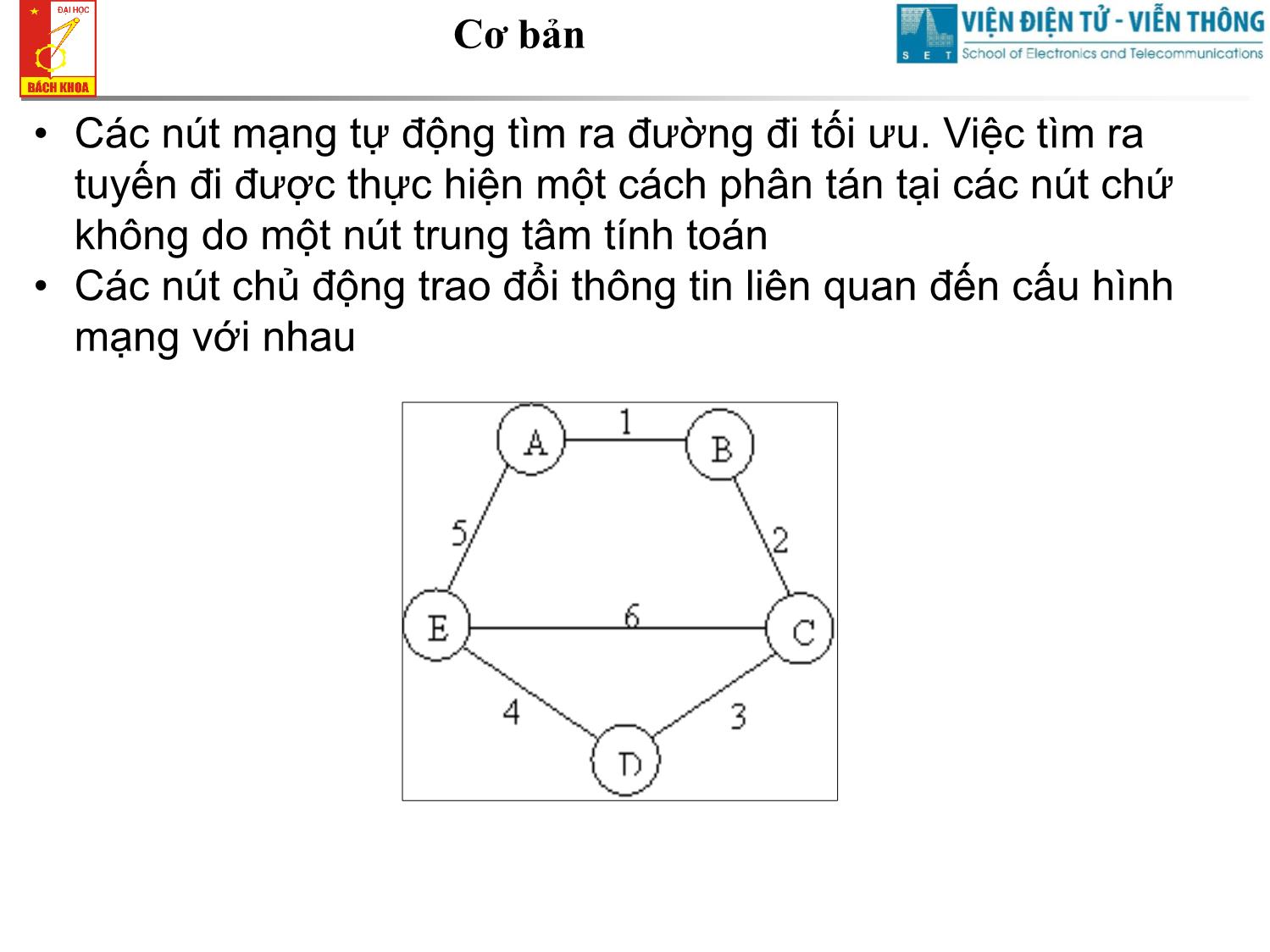
Các nút mạng tự động tìm ra đường đi tối ưu. Việc tìm ra
tuyến đi được thực hiện một cách phân tán tại các nút chứ
không do một nút trung tâm tính toán
• Các nút chủ động trao đổi thông tin liên quan đến cấu hình
mạng với nhauCơ bản
• Từ các thông tin thu thập được, mỗi nút tự tìm ra đường đi tối
ưu đến các nút khác rồi lập ra bảng định tuyến
• Mỗi khi có gói tin đến, nút mạng tra bảng định tuyến đưa ra
quyết định định tuyến
• Bảng định tuyến thường xuyên được cập nhật mỗi khi có thay
đổi cấu hỉnh mạng, tắc nghẽn

Trang 1
Trang 2

Trang 3

Trang 4
Trang 5

Trang 6
Trang 7
Trang 8

Trang 9
Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Cơ sở truyền số liệu - Chương 3: Định tuyến động (Dynamic routing)", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Cơ sở truyền số liệu - Chương 3: Định tuyến động (Dynamic routing)

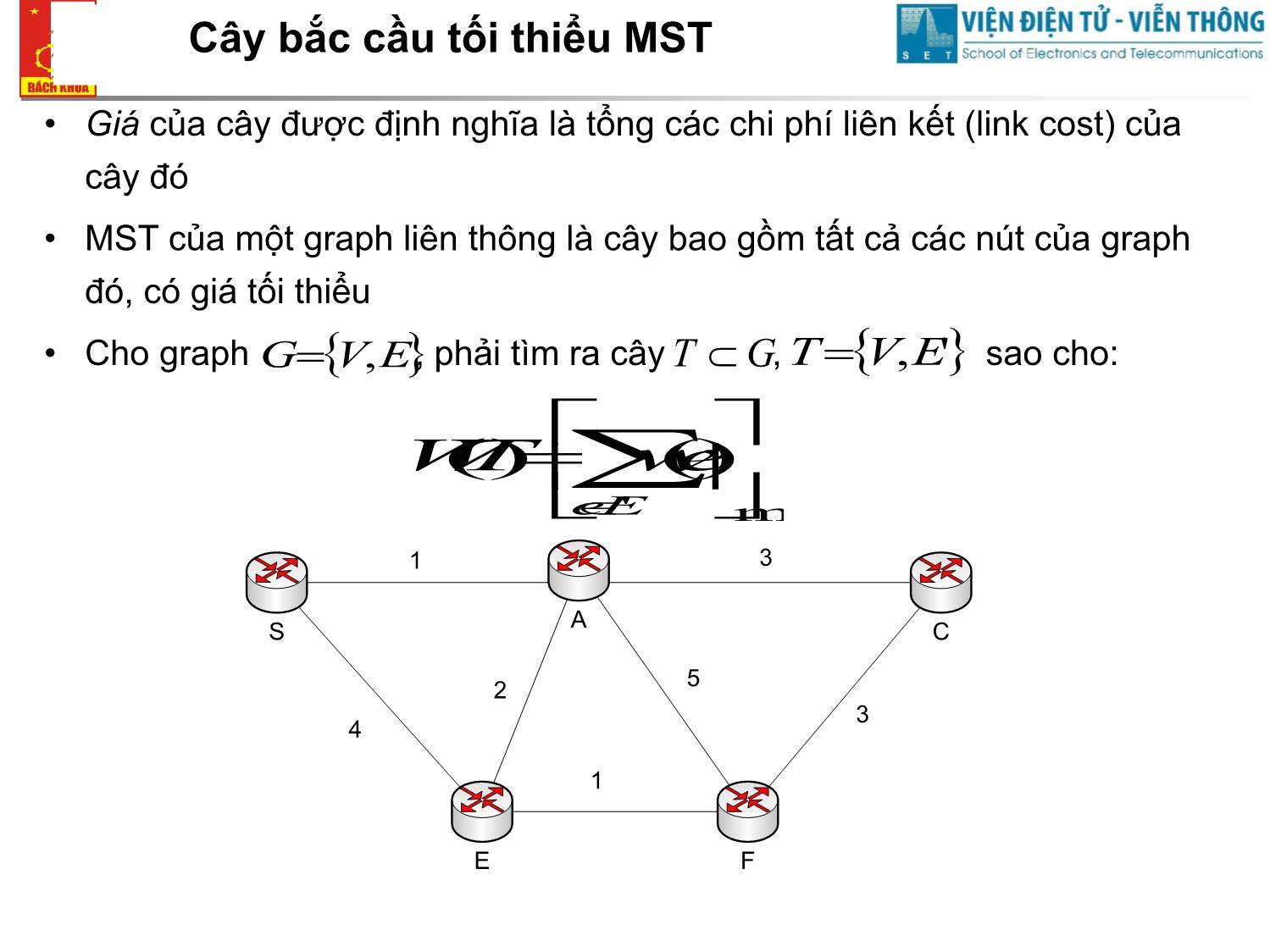
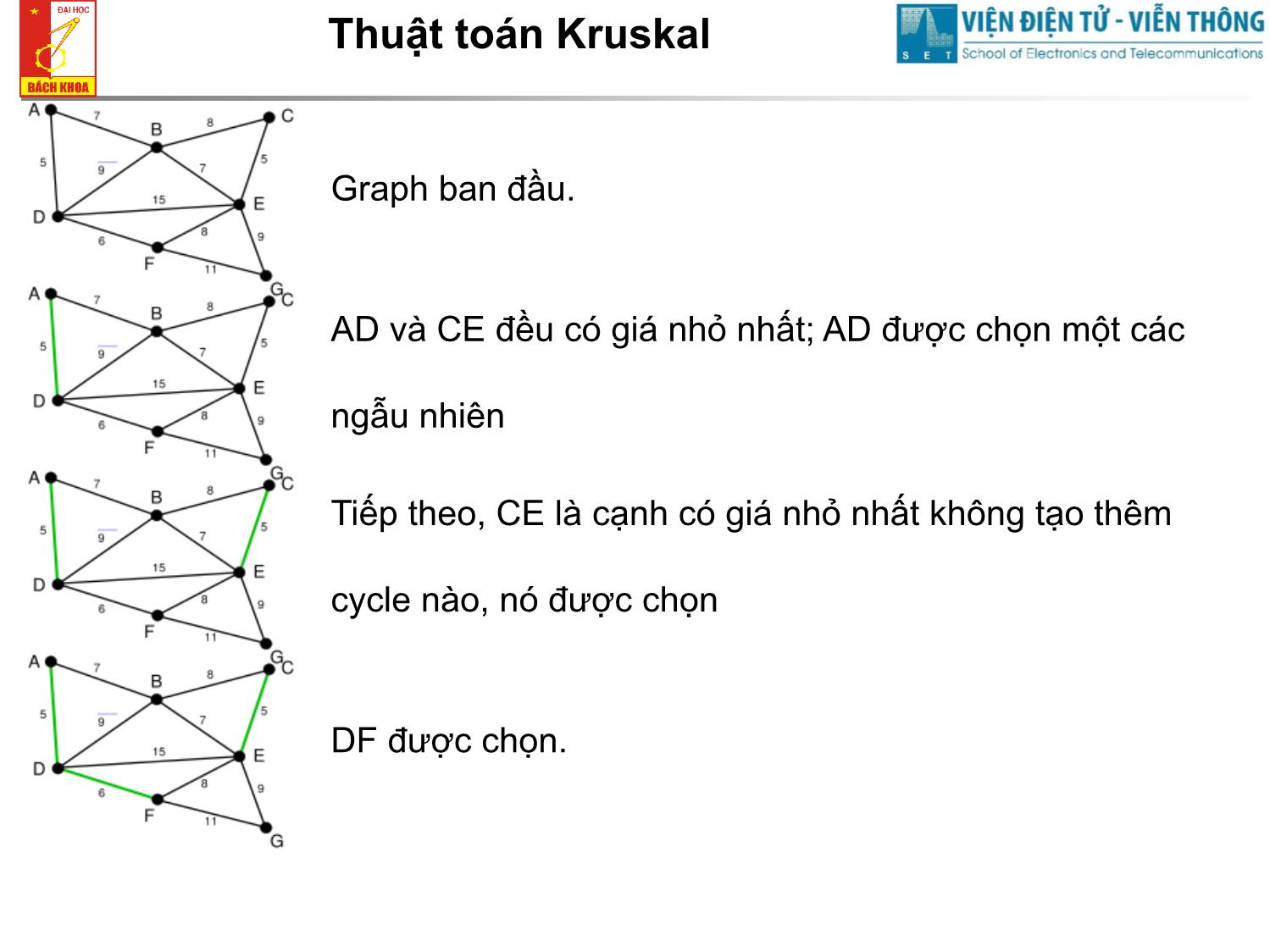
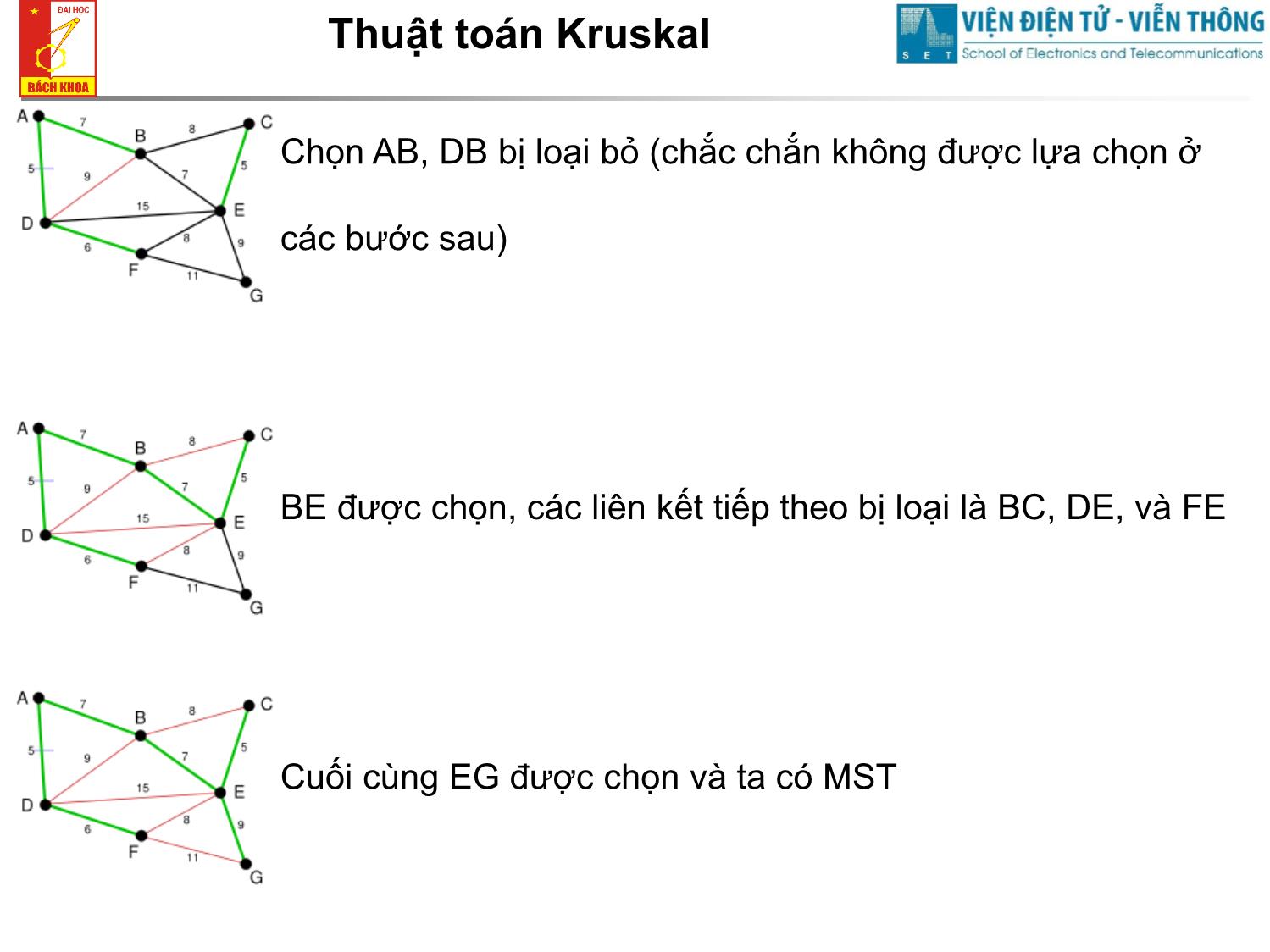
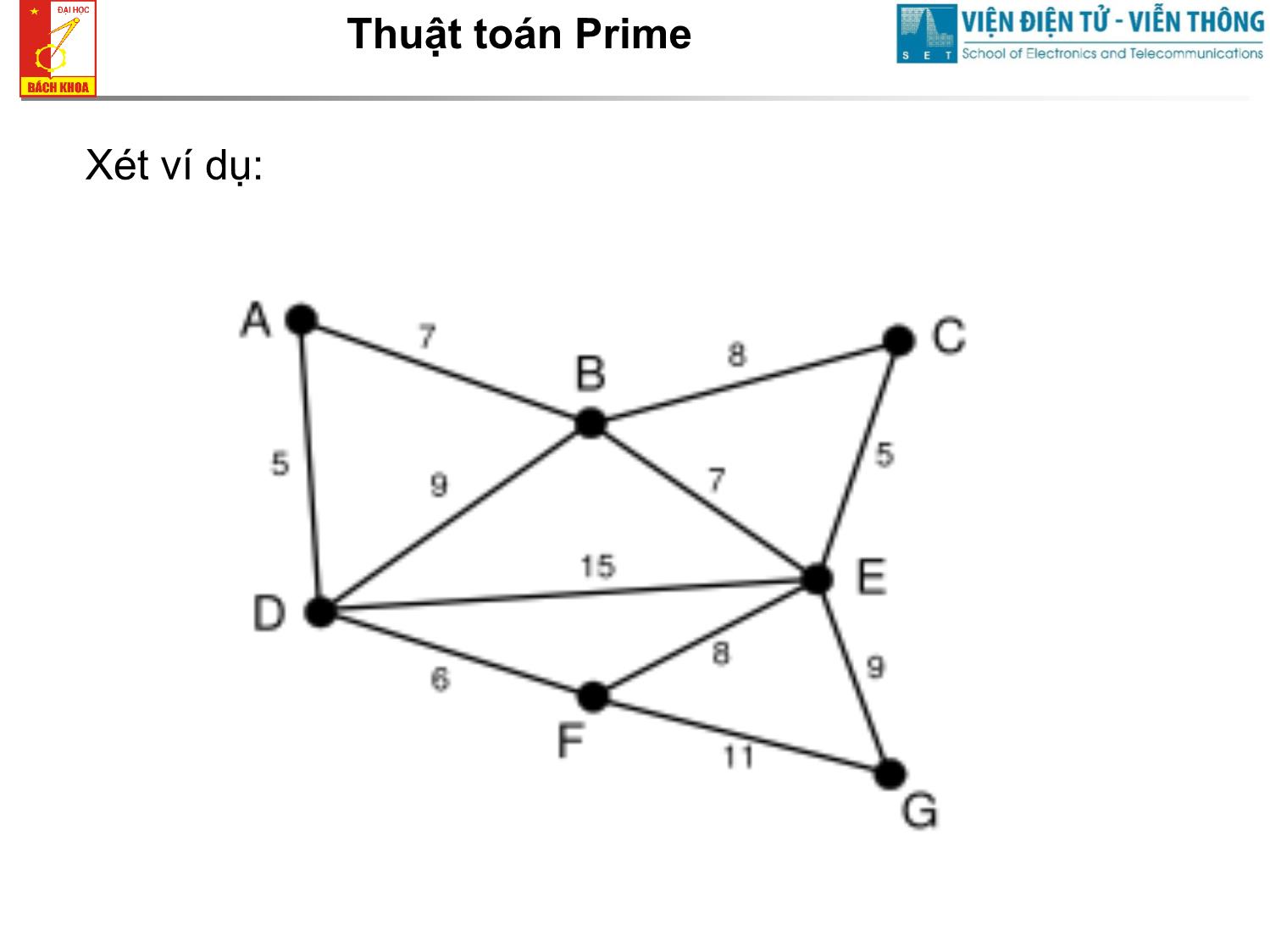
Định tuyến động (dynamic routing) Cơ bản • Các nút mạng tự động tìm ra đường đi tối ưu. Việc tìm ra tuyến đi được thực hiện một cách phân tán tại các nút chứ không do một nút trung tâm tính toán • Các nút chủ động trao đổi thông tin liên quan đến cấu hình mạng với nhau Cơ bản • Từ các thông tin thu thập được, mỗi nút tự tìm ra đường đi tối ưu đến các nút khác rồi lập ra bảng định tuyến • Mỗi khi có gói tin đến, nút mạng tra bảng định tuyến đưa ra quyết định định tuyến • Bảng định tuyến thường xuyên được cập nhật mỗi khi có thay đổi cấu hỉnh mạng, tắc nghẽn Phân loại thuật toán • Cây bắc cầu tối thiểu (MST) • Prime • Kruskal • Cây đường đi ngắn nhất (SPT) • Dijkstra • Bellman Ford Cây bắc cầu tối thiểu MST • Giá của cây được định nghĩa là tổng các chi phí liên kết (link cost) của cây đó • MST của một graph liên thông là cây bao gồm tất cả các nút của graph đó, có giá tối thiểu • Cho graph G V , E , phải tìm ra cây T G , T V , E ' sao cho: W(T) w(e) e E' min 1 3 A S C 2 5 3 4 1 E F Thuật toán Kruskal 1. Khởi tạo: T lúc đầu là một graph rỗng. 2. Nếu T đã gồm đúng n-1 cạnh của G thì T là cây bao trùm cần tìm. Kết thúc. 3. Nếu T còn chưa đủ n-1 cạnh, thì vì G liên thông, nên G có không ít hơn n-1 cạnh; do đó còn các cạnh của G chưa thuộc T. Trong các cạnh của G chưa thuộc T có các cạnh không tạo ra chu trình với các cạnh đã có trong T, chọn cạnh v có trọng số nhỏ nhất trong các cạnh ấy bổ sung (cùng với các đỉnh chưa thuộc T của nó) vào T. Loại bỏ những cạnh tạo thành chu trình. 4. Quay lại 2. Thuật toán Kruskal Graph ban đầu. AD và CE đều có giá nhỏ nhất; AD được chọn một các ngẫu nhiên Tiếp theo, CE là cạnh có giá nhỏ nhất không tạo thêm cycle nào, nó được chọn DF được chọn. Thuật toán Kruskal Chọn AB, DB bị loại bỏ (chắc chắn không được lựa chọn ở các bước sau) BE được chọn, các liên kết tiếp theo bị loại là BC, DE, và FE Cuối cùng EG được chọn và ta có MST Thuật toán Prim 1. Chọn một đỉnh s bất kỳ của G cho vào cây T. Khi đó T là một cây chỉ có một đỉnh và chưa có cạnh nào. 2. Nếu T đã gồm tất cả các đỉnh của G thì T là cây bao trùm cần tìm. Kết thúc. 3. Nếu G còn có các đỉnh không thuộc T, vì G liên thông nên có các cạnh nối một đỉnh trong T với một đỉnh ngoài T, chọn một cạnh có trọng số nhỏ nhất trong số đó cho vào T. 4. Quay lại 2. Thuật toán Prime Xét ví dụ: Nhận xét chung về MST • Có thể tìm được nhiều MST với cùng giá W(T) • Phạm vi áp dụng MST chủ yếu trong mạng LAN
File đính kèm:
 bai_giang_co_so_truyen_so_lieu_chuong_3_dinh_tuyen_dong_dyna.pdf
bai_giang_co_so_truyen_so_lieu_chuong_3_dinh_tuyen_dong_dyna.pdf

