Bài giảng Cấu trúc dữ liệu và thuật toán - Chương 6: Tìm kiếm - Nguyễn Khánh Phương

tion: right-left rotation or left-right rotation) B
Thao tác bổ sung hoặc loại bỏ có thể dẫn đến tình huống 1
 k2 k2 k2
 k1 k1 k1
 C C
 A B B B C
 A A
 • Insertion – Chiều cao • Deletion – Chiều cao của cây
 của cây con A có thể con C có thể giảm đi 1 sau khi
 tăng thêm 1 sau khi bổ loại bỏ
 sung.
Xử lý tình huống 1:
Thực hiện phép quay phải (right rotation)
 k
 2 k1
 right rotation
 k1 k2
 C
 B A B C
 A
 • Thời gian O(1) và khôi phục được cân bằng
Ví dụ: Tình huống 1 xảy ra khi thực hiện bổ sung
 12 12
 k
 2 k1
 8 16 4 16
 k2
 k1 C
 4 10 14 A 2 8 14
 B C
 A 2 6 B 1 6 10
 1
 Insert 1
Xử lý tình huống 2: 
Thực hiện phép quay trái (left rotation)
 k1 k2
 left rotation
 k2 k1
 A
 B A B C
 C
Ví dụ: Tình huống 2 xảy ra sau khi thực hiện loại bỏ
 k1
 5 5 7 k2
 delete 4 left rotation
 4 7 7 k2 5 9
 k
 9 9 1
Xử lý tình huống 3: 
Thực hiện phép quay kép: quay trái rồi quay phải
 k3 k3 k2
 left rotation quanh k1
 right rotation quanh k3
 k2
 k1 k1 k3
 k1
 k2
 C C
 A B2 AB1 B2 C
 A
 B1 B2 B1
Ví dụ: Tình huống 3 sau khi thực hiện bổ sung
 12 12 12
 k
 3 8 16 k 8 16
 3 k2 6 16
 k1
 k1 k3
 4 10 14 k2 6 10 14
 4 8 14
 C C
A k2
 2 6 k1 4
 2 5 10 C
 A B1
 B1 5 2 5
 A B1
không có B
 2 left rotation quanh 4 right rotation quanh 8
Xử lý tình huống 4:
Thực hiện phép quay kép: quay phải rồi quay trái
 right rotation left rotation 
 quanh k3 quanh k1
 k
 k1 1 k2
 k2
 k3 k1 k3
 k3
 k2
 A A
 C B1 AB1 B2 C
 B1 B2 B2 C
Ví dụ
Thuật toán bổ sung (Insertion)
• Chèn nút mới được thực hiện giống như trong cây BST.
• Lần theo đường đi từ nút mới bổ sung về gốc, với mỗi nút x kiểm tra
 | hleft(x)- hright(x) | ≤ 1.
 • Nếu đúng, thì tiếp tục với parent(x). Nếu trái lại, cần khôi phục
 cân bằng nhờ thực hiện phép quay đơn hoặc phép quay kép.
Chú ý: Khi ta đã khôi phục được tính cân bằng của một nút x, thì đồng
thời cũng khôi phục được tính cân bằng của tất cả các tổ tiên của nó.
Nghĩa là việc khôi phục chỉ phải tiến hành với không quá một nút vi
phạm.
Do việc khôi phục cân bằng của một nút đòi hỏi thời gian O(1), nên
thao tác bổ sung đòi hỏi thời gian O(h).
Thuật toán loại bỏ (Deletion) 
• Thực hiện loại bỏ nút x giống như đối với cây BST.
• Tiếp đến duyệt từ nút lá mới đến gốc:
 • Với mỗi nút x trên đường đi, kiểm tra tính cân bằng của nó. Nếu x là cân
 bằng thì tiếp tục với parent(x). Trái lại, khôi phục cân bằng của nút x nhờ
 thực hiện các phép quay.
 • Khác với thuật toán chèn, sau khi khôi phục cân bằng của nút x ta phải tiếp
 tục quá trình cho đến khi gặp gốc của cây, bởi vì việc khôi phục cân bằng
 của nút x không đảm bảo khôi phục được tính cân bằng của tổ tiên của nó.
Dễ thấy việc khôi phục cân bằng của một nút đòi hỏi thời gian O(1), còn đường đi
tới gốc có độ dài không quá h, nên thao tác loại bỏ đòi hỏi thời gian O(h).
Phân tích độ phức tạp
Ta sẽ đưa ra đánh giá chiều cao h của cây AVL với n nút.
• Ký hiệu Th là cây AVL chiều cao h có số lượng nút ít nhất.
Th phải chứa gốc và một cây con với độ cao h 1 còn cây con kia có độ
cao h 2. 
• Do đó, nếu ký hiệu Nh là số lượng nút của Th thì Nh phải thoả mãn
 công thức đệ qui sau đây
 1, khi h 0
 Nh 2, khi h 1
 Nh 1 N h 2 1 khi h 2
Từ đó, chứng minh bằng qui nạp, ta có
 Nh+1= Nh-1 + Nh +1 ≥ Fh+2 1 + Fh+1 = Fh+3 1,
trong đó Fh là số Fibonacci thứ h.
Phân tích độ phức tạp
 . Số Fibonacci thứ n được tính bởi công thức
 1n 1 5 1 5
 F (n ), ,  
 n 5 2 2
 1
 . Ta có NF 1 N h 2 2(||1)  
 h h 2 h 5
 h 2
 (Nh 2) 5 
 log ((Nh 2) 5) h 2
 h log (( Nh 2) 5) 2
 h 1.440log2 ( Nh 2) 0.328
 . Mặt khác, cây AVL với n nút có độ cao thấp nhất là log(n+1), 
 khi nó là cây đầy đủ, tức là ta có
 h ≥ log(n+1). 
Phân tích độ phức tạp
Vậy ta có bất đẳng thức sau đây đối với độ cao của cây AVL với n nút:
 log(n+1) ≤ h ≤ 1.44 log (n+2) 0.328
Do đó h = O(log n)
 Tất cả các phép toán với cây AVL đều được thực hiện với thời gian O(log n)
N i dung
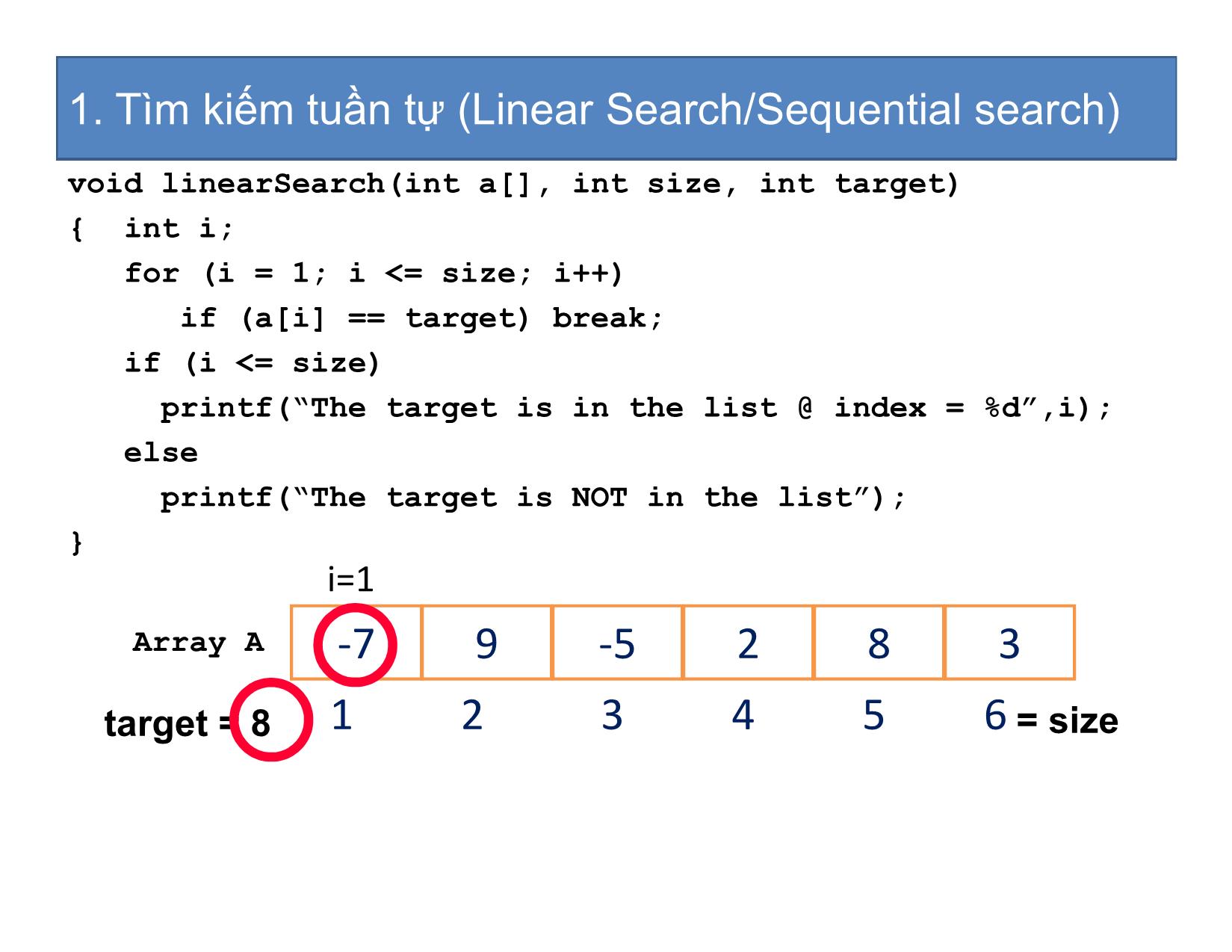
1. Tìm kiếm tuần tự
2. Tìm kiếm nhị phân
3. Cây nhị phân tìm kiếm
4. Cây AVL(Adelson-Velskii và Landis)
5. Bảng băm
 148
5. Bảng băm
5.1. Đặt vấn đề
5.2. Địa chỉ trực tiếp
5.3. Hàm băm
5.1. Đặt vấn đề
. Cho bảng T và bản ghi x, với khoá và dữ liệu đi kèm, ta cần hỗ trợ các thao
 tác sau:
  Insert (T, x)
  Delete (T, x)
  Search(T, x)
. Ta muốn thực hiện các thao tác này một cách nhanh chóng mà không phải
 thực hiện việc sắp xếp các bản ghi.
. Bảng băm (hash table) là cách tiếp cận giải quyết vấn đề đặt ra.
. Trong mục này ta sẽ chỉ xét khoá là các số nguyên dương (có thể rất lớn)
Ứng dụng
. Xây dựng chương trình dịch của ngôn ngữ lập trình (Compiler): Ta cần
 thiết lập bảng ký hiệu trong đó khoá của các phần tử là dãy ký tự tương
 ứng với các từ định danh (identifiers) trong ngôn ngữ lập trình.
. Bảng băm là cấu trúc dữ liệu hiệu quả để cài đặt các từ điển
 (dictionaries).
. Mặc dù trong tình huống xấu nhất việc tìm kiếm đòi hỏi thời gian O(n)
 giống như danh sách móc nối, nhưng trên thực tế bảng băm làm việc
 hiệu quả hơn nhiều. Với một số giả thiết khá hợp lý, việc tìm kiếm phần
 tử trong bảng băm đòi hỏi thời gian O(1).
. Bảng băm có thể xem như sự mở rộng của mảng thông thường. Việc địa
 chỉ hoá trực tiếp trong mảng cho phép truy nhập đến phần tử bất kỳ
 trong thời gian O(1).
5. Bảng băm
5.1. Đặt vấn đề
5.2. Địa chỉ trực tiếp
5.3. Hàm băm
Điạ chỉ trực tiếp (Direct Addressing)
Giả sử tập S gồm n phần tử, trường khóa key của mỗi phần tử x:
  là các số trong khoảng từ 0 đến m-1 (m ≥n)
  các khoá là khác nhau từng đôi
Ta có thể lưu trữ n phần tử này trong một mảng T[0..m-1] trong đó:
  T[i] = x nếu x T và key[x] = i
  T[i] = NULL nếu trái lại
T được gọi là bảng địa chỉ trực tiếp (direct-address table), các phần tử trong bảng T sẽ được gọi
là các ô.
Searching: Nếu cần tìm kiếm phần tử có khóa = k, ta chỉ cần truy cập vào T[k]:
. Nếu T[k] khác NULL return phần tử chứa trong T[k]
. Nếu T[k] = NULL return NULL;
 Tốn O(1)
Các phép toán
Các phép toán được cài đặt một cách trực tiếp:
. DIRECT-ADDRESS-SEARCH(T,k) 
 return T[k] 
. DIRECT-ADDRESS-INSERT(T,x) 
 T[key[x]] = x
. DIRECT-ADDRESS-DELETE(T,x) 
 T[key[x]] = NULL 
Thời gian thực hiện mỗi phép toán đều là O(1).
Hạn chế của phương pháp địa chỉ trực tiếp
. Phương pháp địa chỉ trực tiếp làm việc tốt nếu như biên độ m của các
 khoá là tương đối nhỏ.
. Nếu các khoá là các số nguyên 32-bit thì sao?
  Vấn đề 1: bảng địa chỉ trực tiếp sẽ phải có 232 (hơn 4 tỷ) phần tử
  Vấn đề 2: ngay cả khi bộ nhớ không là vấn đề, thì thời gian khởi
 tạo các phần tử là NULL cũng là rất tốn kém
. Cách giải quyết: Ánh xạ khoá vào khoảng biến đổi nhỏ hơn 0..m-1
. Ánh xạ này được gọi là hàm băm (hash function)
5. Bảng băm
5.1. Đặt vấn đề
5.2. Địa chỉ trực tiếp
5.3. Hàm băm
5.3.Hàm băm
• Trong phương pháp địa chỉ trực tiếp, phần tử với khoá k được cất giữ ở ô k.
• Với bảng băm phần tử với khoá k được cất giữ ở ô h(k), trong đó ta sử dụng hàm băm h
 để xác định ô cất giữ phần tử này từ khoá của nó (k).
• Định nghĩa. Hàm băm h là ánh xạ từ không gian khoá U vào các ô của bảng băm
 T[0..m-1]:
 h : U {0, 1, ..., m-1}
Ta sẽ nói rằng phần tử với khoá k được gắn vào ô h(k) và nói h(k) là giá trị băm của khoá k.
Vấn đề nảy sinh lại là xung đột (collision), khi nhiều khoá được đặt tương ứng với cùng một
ô trong bảng địa chỉ T.
 h(j)=h(k)
5.3.Hàm băm: Giải quyết xung đột
Ta cần giải quyết xung đột như thế nào?
. Cách giải quyết 1:
 Tạo chuỗi (chaining)
. Cách giải quyết 2: 
 Phương pháp địa chỉ mở (open addressing)
 h(j)=h(k)
Giải quyết xung đột: (1) Tạo chuỗi (Chaining)
. Theo phương pháp này, ta sẽ tạo danh sách móc nối để chứa các phần tử được gắn
 với cùng một vị trí trong bảng.
. Ta cần thực hiện bổ sung phần tử như thế nào?
(Như bổ sung vào danh sách móc nối)
. Ta cần thực hiện loại bỏ phần tử như thế nào? Có cần sử dụng danh sách nối đôi
 để thực hiện xoá một cách hiệu quả không? 
(Không ! Vì thông thường chuỗi có độ dài không lớn)
. Thực hiện tìm kiếm phần tử với khoá k cho trước như thế nào?
(Tìm kiếm trên danh sách móc nối trỏ bởi T[h(k)])
Tạo chuỗi (Chaining): Các thao tác
. CHAINED-HASH-INSERT(T, x)
 chèn x vào đầu danh sách móc nối T[h(key[x])]
. CHAINED-HASH-SEARCH(T, k)
 tìm phần tử với khoá k trong danh sách T[h(k)]
. CHAINED-HASH-DELETE(T, x)
 xoá x khỏi danh sách T [h(key[x])]
Phân tích phương pháp chuỗi
. Giả sử rằng thực hiện điều kiện simple uniform hashing: Mỗi khoá trong bảng là
 đồng khả năng được gán với một ô bất kỳ.
. Cho n khoá và m ô trong bảng, ta định nghĩa nhân tử nạp (load factor) = n/m = Số
 lượng khoá trung bình trên một ô
. Khi đó có thể chứng minh được rằng
  Chi phí trung bình để phát hiện một khoá không có trong bảng là O(1+ )
  Chi phí trung bình để phát hiện một khoá có trong bảng là O(1+ )
Do đó chi phí tìm kiếm là O(1+ )
Phân tích tạo chuỗi
. Như vậy chi phí của thao tác tìm kiếm là O(1 + )
. Nếu số lượng khoá n là tỷ lệ với số lượng ô trong bảng thì có giá trị là
 bao nhiêu?
. Trả lời: = O(1)
  Nói cách khác, ta có thể đảm bảo chi phí tìm kiếm mong đợi là hằng
 số nếu ta đảm bảo là hằng số
Giải quyết xung đột: (2) Địa chỉ mở (Open Addressing)
. Ý tưởng cơ bản: 
  Khi bổ sung (Insert): nếu ô là đã bận, thì ta tìm kiếm ô khác, ...., cho đến khi
 tìm được ô rỗng (phương pháp dò thử - probing).
  Để tìm kiếm (search), ta sẽ tìm dọc theo dãy các phép dò thử giống như dãy
 dò thử khi thực hiện chèn phần tử vào bảng.
 Nếu tìm được phần tử với khoá đã cho thì trả lại nó,
 Nếu tìm được con trỏ NULL, thì phần tử cần tìm không có trong bảng
. Ý tưởng này áp dụng tốt khi ta làm việc với tập cố định (chỉ có bổ sung mà
 không có xoá)
  Ví dụ: khi kiểm lỗi chính tả (spell checking)
. Bảng có kích thước không cần lớn hơn n quá nhiều
Giải quyết xung đột: (2) Địa chỉ mở (Open Addressing)
Xét chi tiết 2 kỹ thuật: 
  Dò tuyến tính (Linear Probing)
  Hàm băm kép (Double Hashing)
Dò tuyến tính (Linear Probing)
 Nếu vị trí hiện tại đã bận, ta dò kiếm vị trí tiếp theo trong bảng.
 LinearProbingInsert(k) {
 if (table is full) error;
 probe = h(k);
 while (table[probe] is occupied) 
 probe = (probe+1) % m; //m – kích thước bảng
 table[probe] = k;
 }
Di chuyển dọc theo bảng cho đến khi tìm được vị trí rỗng
. Ưu điểm: Đòi hỏi bộ nhớ ít hơn phương pháp tạo chuỗi (không có móc nối)
. Hạn chế: Đòi hỏi nhiều thời gian hơn tạo chuỗi (nếu đường dò kiếm là dài)
. Thực hiện xoá bằng cách đánh dấu xoá (đánh dấu ô đã bị xoá)
Linear Probing
 Sử dụng hàm băm: h(k) = k % 13
 Chèn: 18, 41, 22, 59, 32, 31, 73
 h(k) : 5, 
 18
 0 1 2 3 4 5 6 7 8 9 10 11 12
Linear Probing
 Sử dụng hàm băm: h(k) = k % 13
 Chèn: 18, 41, 22, 59, 32, 31, 73
 h(k) : 5, 2, 
 41 18
 0 1 2 3 4 5 6 7 8 9 10 11 12
Linear Probing
 Sử dụng hàm băm: h(k) = k % 13
 Chèn: 18, 41, 22, 59, 32, 31, 73
 h(k) : 5, 2, 9, 
 41 18 22
 0 1 2 3 4 5 6 7 8 9 10 11 12
Linear Probing
 Sử dụng hàm băm: h(k) = k % 13
 Chèn: 18, 41, 22, 59, 32, 31, 73
 h(k) : 5, 2, 9, 7, 
 41 18 59 22
 0 1 2 3 4 5 6 7 8 9 10 11 12
Linear Probing
 Sử dụng hàm băm: h(k) = k % 13
 Chèn: 18, 41, 22, 59, 32, 31, 73
 h(k) : 5, 2, 9, 7, 6, 
 41 18 32 59 22
 0 1 2 3 4 5 6 7 8 9 10 11 12
Linear Probing
 Sử dụng hàm băm: h(k) = k % 13
 Chèn: 18, 41, 22, 59, 32, 31, 73
 h(k) : 5, 2, 9, 7, 6, 5,
 41 18 32 59 22
 0 1 2 3 4 5 6 7 8 9 10 11 12
Linear Probing
 Sử dụng hàm băm: h(k) = k % 13
 Chèn: 18, 41, 22, 59, 32, 31, 73
 h(k) : 5, 2, 9, 7, 6, 5,
 41 18 32 59 22
 0 1 2 3 4 5 6 7 8 9 10 11 12
Linear Probing
 Sử dụng hàm băm: h(k) = k % 13
 Chèn: 18, 41, 22, 59, 32, 31, 73
 h(k) : 5, 2, 9, 7, 6, 5,
 41 18 32 59 22
 0 1 2 3 4 5 6 7 8 9 10 11 12
Linear Probing
 Sử dụng hàm băm: h(k) = k % 13
 Chèn: 18, 41, 22, 59, 32, 31, 73
 h(k) : 5, 2, 9, 7, 6, 5,
 41 18 32 59 31 22
 0 1 2 3 4 5 6 7 8 9 10 11 12
Linear Probing
 Sử dụng hàm băm: h(k) = k % 13
 Chèn: 18, 41, 22, 59, 32, 31, 73
 h(k) : 5, 2, 9, 7, 6, 5, 8
 41 18 32 59 31 22
 0 1 2 3 4 5 6 7 8 9 10 11 12
Linear Probing
 Sử dụng hàm băm: h(k) = k % 13
 Chèn: 18, 41, 22, 59, 32, 31, 73
 h(k) : 5, 2, 9, 7, 6, 5, 8
 41 18 32 59 31 22 73
 0 1 2 3 4 5 6 7 8 9 10 11 12
Giải quyết xung đột: (2) Địa chỉ mở (Open Addressing)
Xét chi tiết 2 kỹ thuật: 
  Dò tuyến tính (Linear Probing)
  Hàm băm kép (Double Hashing)
Double Hashing
Ý tưởng: Nếu vị trí hiện tại là bận, tìm vị trí khác trong bảng nhờ sử dụng hai
hàm băm
 DoubleHashInsert(k) {
 if (table is full) error;
 probe = h1(k);
 offset = h2(k);
 while (table[probe] is occupied) 
 probe = (probe+offset) % m; //m – kích thước bảng
 table[probe] = k;
 }
. Dễ thấy: Nếu m là nguyên tố, thì ta sẽ dò thử tất cả các vị trí
. Ưu (nhược) điểm được phân tích tương tự như dò tuyến tính
. Ngoài ra, các khoá được rải đều hơn là dò tuyến tính
Double Hashing
 probe = (probe+offset) % 13;
 h1(k) = k % 13
 h2(k) = 8 – (k % 8)
 Chèn: 18, 41, 22, 59, 32, 31, 73
 h1(k) : 5, 2, 9, 7, 6, 5, 8
 h2(k) : 6, 7, 2, 5, 8, 1, 7
 0 1 2 3 4 5 6 7 8 9 10 11 12
Double Hashing
 probe = (probe+offset) % 13;
 h1(k) = k % 13
 h2(k) = 8 – (k % 8)
 Chèn: 18, 41, 22, 59, 32, 31, 73
 h1(k) : 5, 2, 9, 7, 6, 5, 8
 h2(k) : 6, 7, 2, 5, 8, 1, 7
 41 18 32 5931 22
 0 1 2 3 4 5 6 7 8 9 10 11 12
Double Hashing
 probe = (probe+offset) % 13;
 h1(k) = k % 13
 h2(k) = 8 – (k % 8)
 Chèn: 18, 41, 22, 59, 32, 31, 73
 h1(k) : 5, 2, 9, 7, 6, 5, 8
 h2(k) : 6, 7, 2, 5, 8, 1, 7
 4173 18 32 5931 22
 0 1 2 3 4 5 6 7 8 9 10 11 12
Kết quả lý thuyết: Số phép thử trung bình
 Không tìm được Tìm được
 Chaining 1 1 
 2
 1 1 1 1
 Linear Probing 
 2 2 1 2 2 2 1 
 1 1 1
 Double Hashing ln
 1 1 
 = /
Expected Probes
 Linear Probing
 Double Hashing
 Chaining
 1.0
 0.5 1.0
Chọn hàm băm
. Rõ ràng việc chọn hàm băm tốt sẽ có ý nghĩa quyết định
  Thời gian tính của hàm băm là bao nhiêu?
  Thời gian tìm kiếm sẽ như thế nào?
. Một số yêu cầu đối với hàm băm:
  Phải phân bố đều các khoá vào các ô
  Không phụ thuộc vào khuôn mẫu trong dữ liệu
Hash Functions:
Phương pháp chia (The Division Method)
. h(k) = k mod m
  nghĩa là: gắn k vào bảng có m ô nhờ sử dụng ô xác định bởi phần dư của
 phép chia k cho m
. Điều gì xảy ra nếu m là luỹ thừa của 2(chẳng hạn 2p)?
. Ans: khi đó h(k) chính là p bít cuối của k
. Điều gì xảy ra nếu m là luỹ thừa 10 (chẳng hạn 10p)?
. Ans: khi đó h(k) chỉ phụ thuộc vào p chữ số cuối của k
. Vì thế, thông thường người ta chọn kích thước bảng m là số nguyên tố
 không quá gần với luỹ thừa của 2 (hoặc 10)
Hash Functions:
Phương pháp nhân (The Multiplication Method)
. Phương pháp nhân để xây dựng hàm băm được tiến hành theo hai
 bước. Đầu tiên ta nhân k với một hằng số A, 0 <A< 1 và lấy phần
 thập phân của kA. Sau đó, ta nhân giá trị này với m rồi lấy phần
 nguyên của kết quả:
  Chọn hằng số A, 0 < A < 1:
  h(k) = m (kA - kA ) 
 Phần thập phân của kA
. Chọn m = 2p
. Chọn A không quá gần với 0 hoặc 1
. Knuth: Hãy chọn A = (5 - 1)/2