Bài giảng Cấu trúc dữ liệu và thuật toán - Chương 4: Cây - Nguyễn Khánh Phương
Cây: Định nghĩa đệ quy
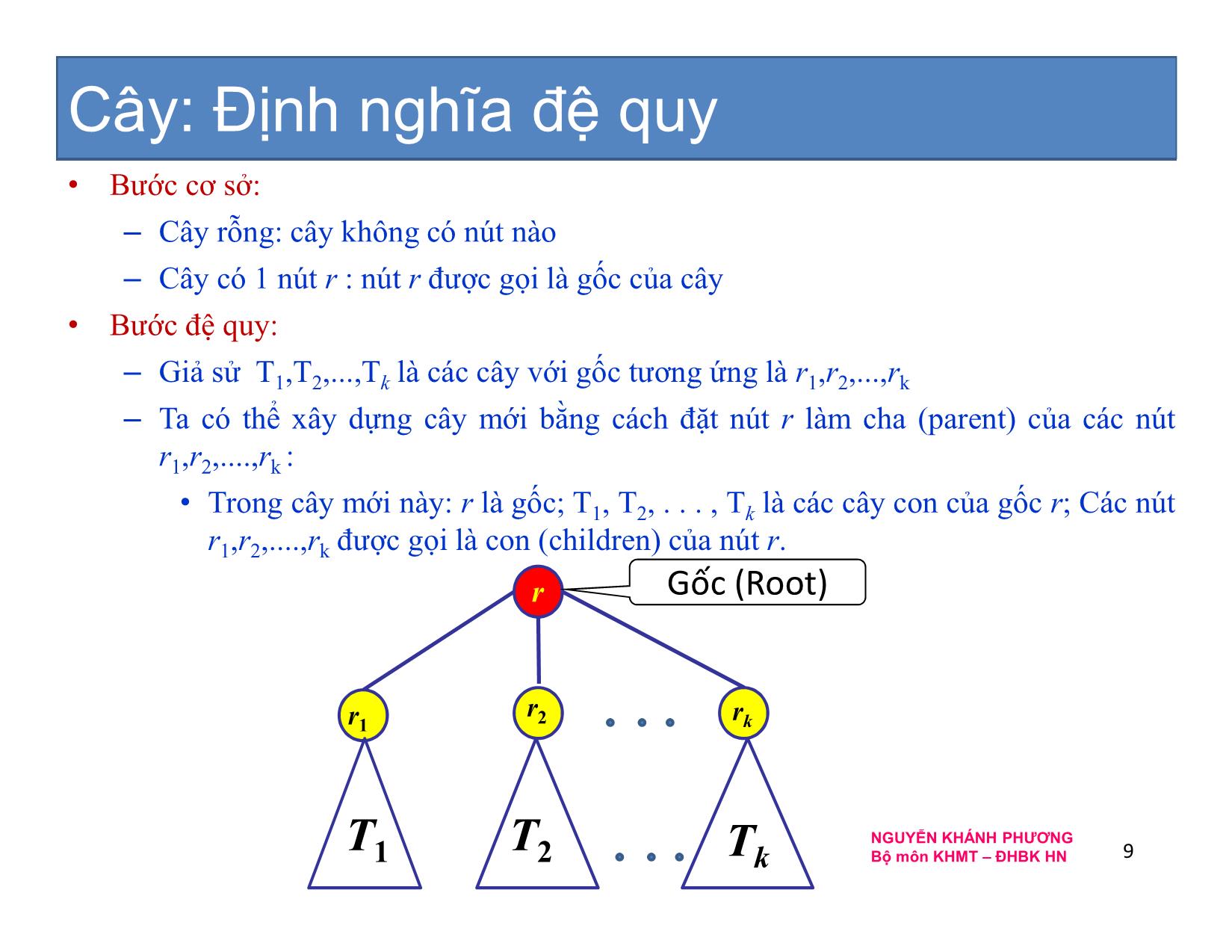
• Bước cơ sở:
– Cây rỗng: cây không có nút nào
– Cây có 1 nút r : nút r được gọi là gốc của cây
• Bước đệ quy:
– Giả sử T
1,T2,.,Tk là các cây với gốc tương ứng là r1,r2,.,rk
– Ta có thể xây dựng cây mới bằng cách đặt nút r làm cha (parent) của các nút
r
1,r2,.,rk :
• Trong cây mới này: r là gốc; T1, T2, . . . , Tk là các cây con của gốc r; Các nút
r
1,r2,.,rk được gọi là con (children) của nút r

Trang 1

Trang 2

Trang 3
Trang 4
Trang 5

Trang 6

Trang 7
Trang 8
Trang 9

Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Cấu trúc dữ liệu và thuật toán - Chương 4: Cây - Nguyễn Khánh Phương", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Cấu trúc dữ liệu và thuật toán - Chương 4: Cây - Nguyễn Khánh Phương

2 to stack 2 15 * Pop 2 3 5 3
2 3 Push 3 to stack 2 3 16 Pop 3 3 5
3 2 Push 2 to stack 2 3 2 17 Evaluate 2*3=6 3 5
4 * Pop 2 2 3 18 Push 6 to stack 3 5 6
5 Pop 3 2 19 - Pop 6 3 5
6 Evaluate 2 * 3 = 6 2 20 Pop 5 3
7 Push 6 to stack 2 6 21 Evaluate 6-5 = 1 3
8 / Pop 6 to stack 2 22 Push 1 to stack 3 1
9 Pop 2 Empty 23 + Pop 1 3
10 Evaluate: 6/2=3 Empty 24 Pop 3 Empty
11 Push 3 to stack 3 25 Evaluate 1 + 3 = 4 Empty
12 5 Push 5 to stack 3 5 26 Push 4 to stack 4
13 3 Push 3 to stack 3 5 3 27 Pop value = 4 Empty
14 2 Push 2 to stack 3 5 3 2
Giá trị biểu thức = 4
145
In biểu thức
Cho cây nhị phân có con trỏ root trỏ đến gốc của cây biểu diễn một biểu thức số học.
Viết hàm in ra biểu thức đó.
• Duyệt cây theo thứ tự giữa:
– In kí tự “(“ trước khi thực hiện duyệt cây con trái
– In ra toán hạng hoặc phép toán có ở trong nút khi thực hiện thăm nút
– In kí tự “)“ sau khi thăm xong cây con phải
void printTree(node *root)
if (root.left != NULL)
{
printf("(");
2 3 2 printTree (root.left);
}
5 1 print(root.data);
if (root.right != NULL)
Gọi printTree(+); {
Biểu thức in ra là: printTree (root.right);
((2 (5 - 1)) + (3 2)) printf (")");
}
Tính giá trị biểu thức số học
Cho cây nhị phân có con trỏ root trỏ vào gốc của cây biểu diễn một biểu thức ố
học. Hãy viết hàm tính giá trị của biểu thức này.
• Duyệt cây theo thứ tự sau (Postorder traversal):
– Tính giá trị các cây con một cách đệ quy
– Thực hiện phép toán ở nút gốc sau khi các cây con trái và phải của nó đã
được tính xong giá trị.
int evaluate (node *root)
{
if (root.left == NULL)//external node
2 3 2 return root.data;
else { //internal node
x = evaluate (root.left);
5 1 y = evaluate (root.right);
gọi OP là phép toán ở nút gốc root.data
z = x OP y
Gọi A = evaluate(+); return z;
}
Giá trị của A là: }
Bài tập: Tính giá trị biểu thức sử dụng stack
Bài tập 1: tính giá trị các kí pháp hậu tố
1) 2 3 + 4 * 5 * Cách 1: Miêu tả bẳng cách vẽ lần lượt trạng thái stack:
2) 27 3 2 ^ / 3 17 * + 27 2 * -
3) 7 6 + 4 * 410 - 5 ^
4) 7 5 – 9 2 / *
Bài tập 2: tính giá trị các kí pháp tiền tố
1) - + 7 * 4 5 + 2 10
2) - * 9 + 2 3 / 27 3 Cách 2: Miêu tả các bước của thuật toán bằng cách kẻ bảng:
Cách 3:
4.4. Một số ứng dụng
4.4.1. Biểu thức số học
4.4.2. Mã Huffman
4.4.3. Cây quyết định
149
Bài tập
• Giả sử ta cần lưu trữ một file gồm 100,000 kí tự. File này chỉ chứa 6 kí tự, với tần suất xuất
hiện như sau:
ab c d e f
Frequency 45000 13000 12000 16000 9000 5000
• Ta sẽ mã hóa mỗi kí tự bởi một xâu nhị phân (gọi là codeword). Do đó, ta cần tìm một dãy
các bit nhị phân mã hóa file này sao cho số bit sử dụng là ít nhất có thể, tức là tìm cách mã
hóa sao cho sử dụng bộ nhớ ít nhất.
• Có hai cách mã hóa:
– Mã hóa với độ dài cố định (fixed-length code): các codeword đều có độ dài bằng nhau.
– Mã hóa với độ dài biến đổi (variable-length code): các codeword có độ dài khác nhau.
• Ví dụ: nếu sử dụng mã với độ dài cố định, thì với file văn bản đã cho, với 6 kí tự, ta cần ít
2 3
nhất 3 bit cho mỗi codeword (vì 2 = 4 < 6, 2 = 8)
ab c d e f
Frequency 45000 13000 12000 16000 9000 5000
A fixed-length 000 001 010 011 100 101
A variable-length 0 101 100 111 1101 1100
Bài tập
• Ví dụ: nếu sử dụng mã với độ dài cố định, thì với file văn bản đã cho, với 6 kí tự, ta cần ít
nhất 3 bit cho mỗi codeword (vì 22 = 4 < 6, 23 = 8)
ab c d e f
Frequency 45000 13000 12000 16000 9000 5000
A fixed-length 000 001 010 011 100 101
A variable-length 0 101 100 111 1101 1100
• Mã hóa với độ dài cố định (fixed length-code) cần:
3 * 100000 = 300000 bits để lưu trữ file đã cho
3 bit chomỗikítự Sốlượngkítựtrongfile
• Mã hóa với độ dài thay đổi (variable-length code) cần:
1 * 45000 + 3*13000+ 3*12000 + 3 * 16000 + 4 * 9000 + 4 * 5000 = 224000 bit
#bit sử dụng để mã hóa kí tự “a” #bit sử dụng để mã hóa kí tự “f”
Tiết kiệm bộ nhớ: 25%
NGUYỄN KHÁNH PHƯƠNG
Bộ môn KHMT – ĐHBK HN
Bài tập
Có thể mã hóa bằng 2 cách:
• Mã hóa với độ dài cố định (fixed-length code): các codeword có độ dài bằng nhau
dễ mã hóa cũng như giải mã, nhưng lại đòi hỏi bộ nhớ lớn.
• Mã hóa với độ dài biến đổi (variable-length code): các codeword có thể có độ dài khác
nhau
– Kí tự có tần suất xuất hiện nhiều nhất (ít nhất) sẽ được mã hóa bởi codeword có độ
dài ngắn nhất (dài nhất).
– Mỗi codeword phải được xác định duy nhất, không phụ thuộc vào độ dài của nó
không có codeword nào là đoạn đầu của một codeword khác (ví dụ: {a = 1, b = 110,
c = 10, d = 111}, thì khi giải mã “1101111” ta thu được xâu ?)
Mã phi tiền tố (Prefix code): là cách mã hóa mỗi kí tự c bởi một xâu nhị phân
code(c) sao cho mã của một kí tự bất kì không là đoạn đầu của bất cứ mã của ký tự nào
trong số các kí tự còn lại (ví dụ: {a = 0, b = 110, c = 10, d = 111} là mã phi tiền tố
ab c d e f
Frequency 45000 13000 12000 16000 9000 5000
A fixed-length 000 001 010 011 100 101
A variable-length 0 101 100 111 1101 1100
Bài toán mã hóa tối ưu (Optimum source coding problem)
• Mã hóa với độ dài biến đổi sử dụng 224000 bit thay vì 300000 bits nếu sử dụng
mã hóa với độ dài cố định tiết kiệm bộ nhớ 25%. Câu hỏi: có cách mã hóa
nào tốt hơn không ? Hay đây đã là cách mã hóa tối ưu (cho chi phí nhỏ nhất) ?
ab c d e f
Frequency 45000 13000 12000 16000 9000 5000
A fixed-length 000 001 010 011 100 101
A variable-length 0 101 100 111 1101 1100
• Bài toán mã hóa tối ưu: Cho bảng kí tự A = {a1, . . . , an} với tần suất xuất hiện
f(ai), hãy tìm mã phi tiền tố C cho bảng kí tự A sao cho số lượng bit cần sử dụng
là nhỏ nhất
�
� �
���
�
Cần để mã hóa file gồm ��� kí tự, với:
– � là xâu nhị phân để mã hóa kí tự � ,
NGUYỄN KHÁNH PHƯƠNG
– � là độ dài của � . Bộ môn KHMT – ĐHBK HN
Bài toán mã hóa tối ưu (Optimum source coding problem)
• Bài toán mã hóa tối ưu: Cho bảng kí tự A = {a1, . . . , an} với tần suất xuất hiện
f(ai), hãy tìm mã phi tiền tố C cho bảng kí tự A sao cho số lượng bit cần sử dụng
là nhỏ nhất
�
� �
���
�
Cần để mã hóa file gồm ��� kí tự, với:
– � là xâu nhị phân để mã hóa kí tự � ,
– � là độ dài của � . David A. Huffman
1925-1999
Huffman đã đề xuất một thuật toán tham lam để giải quyết bài toán mã
hóa tối ưu, tức là xây dựng được một mã phi tiền tố với tổng số bit sử
dụng là ít nhất. Mã đó được gọi là mã Huffman.
NGUYỄN KHÁNH PHƯƠNG
Bộ môn KHMT – ĐHBK HN
4.4.2 Mã Huffman
Thuật toán:
• Bước 1: Lấy 2 kí tự có tần suất xuất hiện nhỏ nhất x, y từ bảng kí tự A, rồi
xây dựng cây con gồm 2 nút lá chứa 2 kí tự này (ý tưởng tham lam). Gán
nhãn cho nút gốc của cây này là z.
• Bước 2: Đặt tần suất xuất hiện f(z) = f(x) + f(y). Xóa x, y và thêm z tạo nên
bảng kí tự mới: � khi đó | �
Lặp lại 2 bước trên, đặt tên là ghép, với bảng kí tự mới � cho đến khi bảng kí
tự chỉ còn gồm 1 kí tự.
Cây thu được chính là mã Huffman
NGUYỄN KHÁNH PHƯƠNG
Bộ môn KHMT – ĐHBK HN
4.4.2 Mã Huffman
• Cho A = {a / 20, b / 15, c / 5, d /15, e / 45} là bảng kí tự cùng tần suất xuất
hiện của các kí tự.
• Bước thứ 1: mã Huffman sẽ ghép c và d
Bảng kí tự mới A1 = {a / 20, b / 15, n1 / 20, e / 45}
• Thuật toán tiếp tục ghép a và b (hoặc có thể ghép b và n1)
Bảng kí tự mới A2 = {n2 / 35, n1: / 20, e / 45}
4.4.2 Mã Huffman
Bảng kí tự mới A2 = {n2 / 35, n1 / 20, e / 45}
Ghép n1 và n2:
Bảng kí tự mới A3 = {n3 / 55, e / 45}
Ghép e và n3, và thuật toán kết thúc
Mã Huffman thu được:
a = 000, b = 001, c = 010, d = 011, e = 1
Là mã phi tiền tố tối ưu
(cho tổng số bít sử dụng ít nhất)
4.4.2 Mã Huffman
• Tần suất của các kí tự trong văn bản:
Char Freq
E 125
T 93
A 80
O 76
I 72
N 71
S 65
R 61
H 55
L 41
D 40
C 31
U 27
4.4.2 Mã Huffman
A O T E
80 76 93 125
D L R S N I H
40 41 61 65 71 73 55
C U
31 27
4.4.2 Mã Huffman
A O T E
80 76 93 125
D L R S N I H
40 41 61 65 71 73 58 55
C U
31 27
4.4.2 Mã Huffman
A O T E
80 76 81 93 125
D L R S N I H
40 41 61 65 71 73 58 55
C U
31 27
4.4.2 Mã Huffman
A O T E
80 76 81 93 125 113
D L R S N I H
40 41 61 65 71 73 58 55
C U
31 27
4.4.2 Mã Huffman
A O T E
80 76 81 93 126 125 113
D L R S N I H
40 41 61 65 71 73 58 55
C U
31 27
4.4.2 Mã Huffman
A O T E
80 76 81 93 126 144 125 113
D L R S N I H
40 41 61 65 71 73 58 55
C U
31 27
4.4.2 Mã Huffman
156
A O T E
80 76 81 93 126 144 125 113
D L R S N I H
40 41 61 65 71 73 58 55
C U
31 27
4.4.2 Mã Huffman
156 174
A O T E
80 76 81 93 126 144 125 113
D L R S N I H
40 41 61 65 71 73 58 55
C U
31 27
4.4.2 Mã Huffman
156 174
238
A O T E
81 126 144 113
D L R S N I H
58
C U
4.4.2 Mã Huffman
156 174 270
238
A O T E
80 76 81 93 126 144 125 113
D L R S N I H
40 41 61 65 71 73 58 55
C U
31 27
4.4.2 Mã Huffman
330
156 174 270
238
A O T E
80 76 81 93 126 144 125 113
D L R S N I H
40 41 61 65 71 73 58 55
C U
31 27
4.4.2 Mã Huffman
330 508
156 174 270
238
A O T E
80 76 81 93 126 144 125 113
D L R S N I H
40 41 61 65 71 73 58 55
C U
31 27
4.4.2 Mã Huffman
0 1
838
0 330 1 0 508 1
0 1
1560 174 1 270 0 1
0 1 238
A O T E
80 76
0 81 193 0126 1 0 144 1 125 0 113 1
D L R S N I H
40 41 61 65 71 73 0 58 1 55
C U
31 27
4.4.2 Mã Huffman
Char Frequency Fixed-length code Huffman code
E 125 0000 110
T 93 0001 011
A 80 0010 000
O 76 0011 001
I 73 0100 1011
N 71 0101 1010
S 65 0110 1001
R 61 0111 1000
H 55 1000 1111
L 41 1001 0101
D 40 1010 0100
C 31 1011 11100
U 27 1100 11101
Sum 838 3352 3036
• Sử dụng mã Huffman: tiết kiệm bộ nhớ 10%
• Mã Huffman là ví dụ đơn giản của mã hóa dữ liệu
NGUYỄN KHÁNH PHƯƠNG
Bộ môn KHMT – ĐHBK HN
4.4.2 Mã Huffman: giải mã
• Thuật toán giải mã:
– Đọc file nén & xây dựng cây nhị phân
– Sử dụng cây nhị phần để giải mã
• Đi từ nút gốc đến nút lá
• Ví dụ: Giải mã “11100000011”
4.4. Một số ứng dụng
4.4.1. Biểu thức số học
4.4.2. Mã Huffman
4.4.3. Cây quyết định (Decision tree)
174
4.4.2 Mã Huffman: giải mã
procedure Huffman_Decode(B)
//B là xâu mã hóa văn bản theo mã Huffman
begin
While do
begin
x bit tiếp theo trong xâu B;
If x = 0 then P Con trái của P
Else P Con phải của P
If (P là nút lá) then
begin
end;
end;
end;
4.4.3. Cây quyết định (Decision Tree)
• Cây quyết định là một cây mà mỗi đỉnh trong của nó tương ứng với một truy
vấn đối với dữ liệu. Các cạnh của cây tương ứng với các khả năng trả lời cho
câu hỏi. Mỗi lá của cây tương ứng với một đầu ra.
• Để tính toán với cây quyết định chúng ta sẽ bắt đầu từ gốc và di chuyển theo
một đường đi đến lá. Tại mỗi nút trung gian câu trả lời cho truy vấn đối với
dữ liệu sẽ dẫn ta đến nút tiếp theo. Khi đạt đến lá ta thu được một đầu ra.
NGUYỄN KHÁNH PHƯƠNG
Bộ môn KHMT – ĐHBK HN
4.4.3. Cây quyết định
Ví dụ. Bài toán tra từ điển. Cho mảng A gồm n số được sắp theo thứ tự tăng dần và một số
x. Cần xác định xem x có mặt trong mảng đã cho hay không. Nếu câu trả lời là khẳng định
cần chỉ rõ vị trí của x trong mảng A.
• Cây quyết định để giải bài toán này có dạng một cây nhị phân:
– Mỗi nút trong của cây quyết định chứa một câu hỏi dạng: “x < k ?”
– Mỗi nút ở mức sát lá của cây quyết định chứa câu hỏi : “x = A[i]?”
có hai con, một con ứng với ‘i’ còn một con ứng với ‘-’ (không có).
Ví dụ: Xét A = (2, 3, 5, 7, 11, 13, 17, 19). Cây quyết định có dạng sau đây
4.4.3. Cây quyết định
• Ta xác định thời gian của thuật toán cây quyết định là số truy vấn
trên đường đi từ gốc đến lá. Như vậy, thời gian tính trong tình
huống xấu nhất của thuật toán sẽ là độ cao của cây quyết định.
• Nếu ta hạn chế chỉ được sử dụng phép so sánh để giải bài toán tra
từ điển, thì rõ ràng hoạt động của mọi thuật toán giải bài toán tra từ
điển đều có thể mô tả bởi cây quyết định.
• Do đó nếu đánh giá được cận dưới cho độ cao của cây quyết định
(thuật toán) giải bài toán tra từ điển thì ta cũng thu được cận dưới
cho độ phức tạp của bài toán.
NGUYỄN KHÁNH PHƯƠNG
Bộ môn KHMT – ĐHBK HN 178
4.4.3. Cây quyết định
• Giả thiết rằng: “Các truy vấn đối với dữ liệu phải đảm bảo đủ thông tin để có thể xác
định được đầu ra có thể”.
• Nếu bài toán có N đầu ra có thể thì rõ ràng mọi cây quyết định đều có N lá (không loại
trừ tình huống khi có một số lá tương ứng với cùng một đầu ra).
• Từ bổ đề 1, ta biết rằng: Nếu một cây có n lá và mỗi nút có nhiều nhất 2 nút con (mỗi
truy vấn có nhiều nhất 2 câu trả lời) thì độ cao của cây ít nhất sẽ là
log n = (log n)
• Áp dụng kết quả này: Với bài toán tra từ điển với tập S gồm n phần tử, do bài toán có tất
cả n+1 đầu ra có thể, nên mọi cây quyết định có n+1 lá, và vì thế, có độ cao ít nhất là
log (n+1) = (log n).
• Suy ra: Mọi thuật toán giải bài toán tra từ điển chỉ sử dụng phép so sánh đều có
thời gian tính là (log n).
• Như đã biết: Thuật toán tìm kiếm nhị phân có thời gian tính là O(log n). Từ các kết quả
trên suy ra: “Thuật toán tìm kiếm nhị phân là thuật toán nhanh nhất trong số các
thuật toán chỉ sử dụng phép so sánh để giải bài toán tra từ điển”. 179
Bài toán sắp xếp
• Cho dãy n số phân biệt (a[1], a[2], ..., a[n]), tìm hoán vị =( (1), (2), ..., (n)) sao
cho: a[ (1)] < a[ (2)] < ... < a[ (n)].
• Giả sử ta chỉ sử dụng phép so sánh để thực hiện sắp xếp, khi đó mọi thuật toán sắp
xếp đều có thể diễn tả trong mô hình cây quyết định. Cây quyết định là cây nhị phân
thoả mãn:
– Mỗi nút một phép so sánh "a < b"
• cũng có thể coi tương ứng với một không gian con các trình tự
– Mỗi cạnh rẽ nhánh theo câu trả lời (true hoặc false)
– Mỗi lá 1 trình tự sắp xếp
– Cây quyết định có bao nhiêu lá, nếu có n phần tử phân biệt cần sắp xếp?
• n!, tức là tất cả các trình tự có thể
• Đối với mỗi bộ dữ liệu, chỉ có 1 lá chứa trình tự sắp xếp cần tìm
NGUYỄN KHÁNH PHƯƠNG
Bộ môn KHMT – ĐHBK HN 180
Cây quyết định cho bài toán sắp xếp ba số a, b, c
a < b < c, b < c < a,
c < a < b, a < c < b,
b < a < c, c < b < a
a < b < c "a < b?" b < c < a
a > b
c < a < b a < b b < a < c
a < c < b c < b < a
"a < c?" "b < c?"
a c b c
a < b < c c < a < b b < c < a c < b < a
a < c < b b < a < c
"b < c?" "c < a?"
b c c a
a < b < c a < c < b b < c < a b < a < c
Mỗi lá tương ứng với một trình tự sắp xếp ba số a, b, c
181
Bài toán sắp xếp
• Do có tất cả n! hoán vị, nên mọi cây quyết định giải bài toán sắp xếp yêu
cầu ít nhất n! lá, vì thế có độ cao ít nhất là (log n!).
Ta có:
log n! = log 1+log 2 +...+ logn
≥ log(n/2) + log(n/2+1) +...+ log n
≥ (n/3) log(n/2)
= (1/3) (n log n - n log 2)
= (n log n).
• Như vậy, ta đã chứng minh được kết quả sau đây:
"Mọi thuật toán sắp xếp chỉ sử dụng phép so sánh đều đòi hỏi thời
gian (n log n)".
NGUYỄN KHÁNH PHƯƠNG
Bộ môn KHMT – ĐHBK HN 182File đính kèm:
 bai_giang_cau_truc_du_lieu_va_thuat_toan_chuong_4_cay_nguyen.pdf
bai_giang_cau_truc_du_lieu_va_thuat_toan_chuong_4_cay_nguyen.pdf

