Bài giảng Cấu trúc dữ liệu và thuật toán - Chương 3: Các cấu trúc dữ liệu cơ bản - Nguyễn Khánh Phương
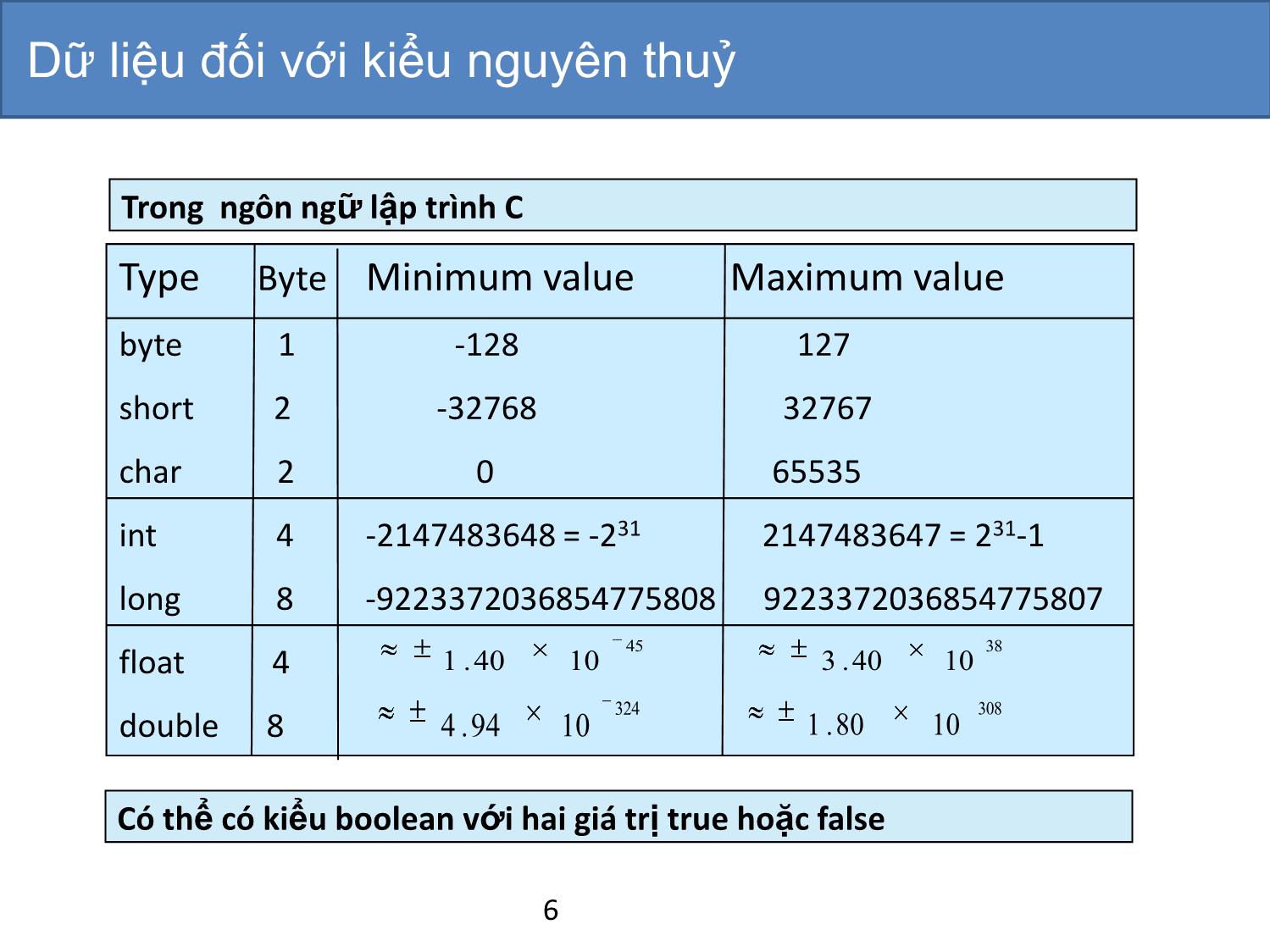
Kiểu dữ liệu (Data types)
• Kiểu dữ liệu (data type) được đặc trưng bởi:
– Tập các giá trị (a set of values);
– Cách biểu diễn dữ liệu (data representation) được sử dụng chung
cho tất cả các giá trị này và
– Tập các phép toán (set of operations) có thể thực hiện trên tất cả
các giá trị.
• Chú ý:
– Mỗi giá trị có một cách biểu diễn nào đó mà người sử dụng
không nhất thiết phải biết
– Mỗi phép toán được cài đặt theo một cách nào đó mà người sử
dụng cũng không cần phải biết

Trang 1

Trang 2

Trang 3

Trang 4

Trang 5
Trang 6

Trang 7

Trang 8

Trang 9
Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Cấu trúc dữ liệu và thuật toán - Chương 3: Các cấu trúc dữ liệu cơ bản - Nguyễn Khánh Phương", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Cấu trúc dữ liệu và thuật toán - Chương 3: Các cấu trúc dữ liệu cơ bản - Nguyễn Khánh Phương

ĐHBK HN
Cài đặt hàng đợi Queue: dùng mảng (Array)
• Cách 2: hàng đợi Q vòng tròn,[quấn quanh] • Q[front]: phần tử đầu tiên của Q
• Q[rear]: phần tử cuối cùng của Q
(circular queue [“wrap around”]) • Thêm phần tử vào Q (Enqueue): rear+=1;Q[rear]=item;
Ví dụ 1: Mảng có maxSize = 4; • Xóa phần tử khỏi Q (Dequeue): xóa Q[front]; sau đó front+=1
Khởi tạo: Q rỗng: front = 0; rear = -1;
enqueue(Q,2) enqueue(Q,3) enqueue(Q,5) dequeue(Q) dequeue(Q) enqueue(Q,10)
rear ++; rear++; rear++; Dequeue Q[front] Dequeue Q[front] rear++;
Q[rear] = 2; Q[rear] = 3; Q[rear] = 5; Q = (3, 5) Q = (5) Q[rear] = 10;
Q = (2) Q = (2, 3) Q = (2, 3, 5)
front++; front++; Q = (5,10)
enqueue(Q,20) ???
Thực hiện quấn quanh
“wrap around”
If (rear == maxSize -1)
rear = 0;
else
rear ++; rear = rear +1;
Q = (5,10, 20) Q vòng tròn
Q[rear] = 20; Or
rear = 4 = maxSize (Circular queue)
rear = (rearmaxSize + 1) %;
Mảng Q tràn (over flow)
Cài đặt hàng đợi Queue: dùng mảng (Array)
• Cách 2: hàng đợi Q vòng tròn,[quấn quanh] • Q[front]: phần tử đầu tiên của Q
• Q[rear]: phần tử cuối cùng của Q
Ví dụ 2: Mảng có kích thước maxSize = 4 • Thêm phần tử vào Q (Enqueue): rear+=1;Q[rear]=item;
• Xóa phần tử khỏi Q (Dequeue): xóa Q[front]; sau đó front+=1
Q gồm 3 phần tử: Q = (5, 10, 20)
enqueue(Q,30) enqueue(Q,50) ?? Thêm 50 vào Q khi Q đã đầy
Q đã đầyl!!!
Làm thế nào để kiểm tra được Q đã đầy ?
rear + 1 == front
rear++; rear++;
Q[rear] = 30; Q[rear] = 50; Nếu vậy ta không phân biệt được 2 trường
Q = (5, 10, 20, 30) rear = 2 = front hợp: hàng đợi Q
RỖNG VÀ ĐẦY!!
dequeue(Q) dequeue(Q) dequeue(Q) dequeue(Q)
Q đã rỗng!!!
Làm thế nào để kiểm tra được Q rỗng ?
rear + 1 == front
Dequeue Q[front] Dequeue Q[front] Dequeue Q[front]
Q = (20, 30) Dequeue Q[front]
Q = (10, 20, 30) front++; Q = (30) Q = empty
front++; => front = 4=maxSize front++;
=> “wrap around” front++;
front = 0
Cài đặt hàng đợi Queue: dùng mảng (Array)
• Cách 2: hàng đợi Q vòng tròn,[quấn quanh]
Giải pháp 1: Dùng biến front trỏ tới phần tử ngay trước phần tử đầu Q (khi đó, 1 ô nhớ sẽ không
được dùng tới -> lãng phí 1 ô nhớ).
Make front point to the element preceding the front element in the queue (one memory
location will be wasted).
NGUYỄN KHÁNH PHƢƠNG
Bộ môn KHMT – ĐHBK HN
Ví dụ 3: mô phỏng giải pháp 1
Giải pháp 1: Dùng enqueue(Q, 30)
biến front trỏ tới
phần tử ngay trước Q đã đầy!!!
phần tử đầu Q (khi Làm thế nào để kiểm tra
đó, 1 ô nhớ sẽ lãng Q đã đầy ?
phí không được
dùng tới)
rear + 1 == front
Make front point to
Q = (10, 20) the element Q = (10, 20) rear++; Q[rear] = 30;
preceding the front Q = (10, 20, 30)
elementdequeue in the(Q) dequeue(Q) dequeue(Q)
queue (one
memory location
will be wasted). Q đã rỗng!!!
Làm thế nào để kiểm tra Q
đã rỗng ?
rear == front
Q = (10, 20, 30)
front++; front++; front++;
Dequeue Q[front] front = 4 = maxSize Dequeue Q[front]
Q = (20, 30) wrap around: front = 0 Q = empty
Dequeue Q[front]
Q = (30)
Dùng giải phápô nhớ1, mộtcủa mảng sẽ bị lãng phí vì khôngdùngđƣợctới!!!
Cài đặt hàng đợi Queue: dùng mảng (Array)
• Cách 2: hàng đợi Q vòng tròn,[quấn quanh]
Giải pháp 1: Dùng biến front trỏ tới phần tử ngay trước phần tử đầu Q (khi đó, 1 ô nhớ sẽ không
được dùng tới -> lãng phí 1 ô nhớ)
Giá trị khởi tạo ban đầu của 2 biến front và rear ?
front = rear = maxSize – 1;
Hàng đợi Q chỉ chứa được tối đa (maxSize – 1) phần tử, các phần tử nằm lần lượt từ
Q[front+1] đến Q[rear]
Hàng đợi Q đầy khi: rear + 1 == front
Hàng đợi Q rỗng khi: rear == front
• Q[front+1]: phần tử đầu tiên của hàng đợi
Make• Q[rear] front point: phần to tửthecuối elementcùng precedingcủa hàng đợithe front element in the queue (one memory
•locationThêm will(Enqueue be wasted).) 1 phần tử mới vào Q : rear+=1; Q[rear]=item
• Xóa (Dequeue) 1 phần tử khỏi Q : front+=1; sau đó xóa Q[front] khỏi hàng đợi
Ví dụ 4: Mảng có maxSize = 4
Khởi tạo: front = rear = maxSize – 1 = 3; Mô phỏng giải pháp 1
Q rỗng
Khởi tạo: front=rear=3; enqueue(Q, 2) enqueue(Q, 3) enqueue(Q, 5) dequeue(Q)
rear++; rear++; rear++; front++;
Q[rear] = 2; Q[rear] = 3; Q[rear] = 5; => front = 4 = maxSize
Q= (2) Q= (2, 3) Q= (2, 3, 5) => wrap around : front = 0
Dequeue Q[front]
Q= (3, 5)
rear + 1 == front
Hàng đợi Q đầy!!!
dequeue(Q) enqueue(Q, 10) enqueue(Q, 20)
Tổng quát:kiểm tra Q đầy:
(rear + 1)% maxSize == front
enqueue(Q, 30) ??
ERROR: Q đầy
front++; rear++; rear++;
dequeue Q[front] Q[rear] =10; Q[rear] =20;
Q= (5, 10) Q= (5, 10, 20)
Q= (5)
Ví dụ 4: Mảng có maxSize = 4
Khởi tạo: front = rear = maxSize – 1 = 3; Mô phỏng giải pháp 1
Q rỗng
dequeue(Q) dequeue(Q) dequeue(Q)
Q= (5, 10, 20) front++; front++; front++;
Dequeue Q[front] Dequeue Q[front] =>front = 4 = maxSize
Q= (10, 20) Q= (20) => wrap around: front =0
Dequeue Q[front]
Q empty
Hàng đợi Q rỗng !!!
rear == front
Cài đặt hàng đợi Queue: dùng mảng (Array)
• Cách 2: hàng đợi Q vòng tròn,[quấn quanh]
Giải pháp 1: Dùng biến front trỏ tới phần tử ngay trước phần tử đầu Q (khi đó, 1 ô nhớ sẽ không
được dùng tới -> lãng phí 1 ô nhớ)
• Giá trị ban đầu của biến front và rear :
front = rear = maxSize – 1;
• Q[front+1]: phần tử đầu hàng đợi
• Q[rear]: phần tử cuối hàng đợi
• Thêm (Enqueue) 1 phần tử item vào hàng đợi Q :
– rear+=1; if (rear == maxSize) rear = 0;
– Q[rear]=item
• Xóa (Dequeue) 1 phần tử khỏi hàng đợi Q :
– front = (front + 1) % maxSize;
– sau đó xóa phần tử Q[front] khỏi hàng đợi
• Hàng đợi rỗng nếu : rear == front
• Hàng đợi đầy nếu: (rear + 1) % maxSize == front in the queue (one memory location
will be wasted).
Cài đặt cho Giải pháp 1: Dùng biến front trỏ tới phần tử ngay trước phần tử đầu Q (khi
đó, 1 ô nhớ sẽ không được dùng tới -> lãng phí 1 ô nhớ)
init(int max) //khởi tạo hàng đợi Q rỗng
{
maxSize = max;
front = maxSize – 1;
rear = maxSize – 1;
Q = new ItemType[maxSize];
}
int sizeQ(Q) //hàm trả về số lượng phần tử đang có trong hàng đợi Q
{
int size = (maxSize – front + rear) % maxSize;
return size;
}
Q = (5, 10, 20)
Q = (10, 20)
số phần tử = (4 – 1+ 0) % 4 = 3
số phần tử = (4 – 2+ 0) % 4 = 2
241
Cài đặt cho Giải pháp 1: Dùng biến front trỏ tới phần tử ngay trước phần tử đầu Q (khi
đó, 1 ô nhớ sẽ không được dùng tới -> lãng phí 1 ô nhớ)
isEmpty(Q) // trả về giá trị "true“ nếu hàng đợi Q là rỗng(empty)
{
if (rear == front) return true;
else return false;
}
isFull(Q) /*hàm trả về giá trị “true” nếu hàng đợi Q đầy (full), tức là đã dùng hết bộ nhớ dành cho Q; ngược lại hàm
trả về giá trị “false” */
{
if ((rear + 1) % maxSize == front) return true;
else return false;
}
frontQ(Q) //hàm trả về giá trị phần tử đầu (front (head)) hàng đợi, hoặc trả về thông báo error nếu Q đã đầy.
{
return Q[front + 1];
}
242
Cài đặt cho Giải pháp 1: Dùng biến front trỏ tới phần tử ngay trước phần tử đầu Q (khi
đó, 1 ô nhớ sẽ không được dùng tới -> lãng phí 1 ô nhớ)
enqueue(Q,x) /*hàm thêm phần tử x vào phía sau (back (rear)) hàng đợi Q. Nếu Q đã đầy trước khi thêm, cần thông báo: Q đã đầy,
không thể thêm*/
{
if (isFull(Q)) ERROR(“Queue is FULL”);
else
{ rear ++;
if (rear == maxSize) rear = 0;
Q[rear] = x;
}
}
enqueue(Q,x)
{
if (isFull(Q)) ERROR(“Queue is FULL”);
else
{ rear = (rear + 1) % maxSize;
Q[rear] = x;
}
} 243
Cài đặt cho Giải pháp 1: Dùng biến front trỏ tới phần tử ngay trước phần tử đầu Q (khi
đó, 1 ô nhớ sẽ không được dùng tới -> lãng phí 1 ô nhớ)
dequeue(Q) /*deletes the element at the front (head) of the queue Q, then returns x which is the data of this element. If the queue Q is empty
before dequeue, then give the error notification*/
{
if (isEmpty(Q)) ERROR(“Queue is EMPTY”);
else
{ front = (front + 1);
if (front == maxSize) front = 0;
return Q[front];
}
}
dequeue(Q) //Một cách viết khác:
{ if (isEmpty(Q)) ERROR(“Queue is EMPTY”);
else
{ front = (front + 1) % maxSize;
return Q[front];
}
} front = front + 1;
=>front = 4 = maxSize
Dequeue (Q)
=> wrap around: front =0
Dequeue Q[front]
Q empty 244
Cài đặt hàng đợi Queue: dùng mảng (Array)
• Cách 2: hàng đợi Q vòng tròn,[quấn quanh] (circular queue [“wrap around”])
Giải pháp 1: Dùng biến front trỏ tới phần tử ngay trước phần tử đầu Q (khi đó, 1 ô nhớ sẽ không
được dùng tới -> lãng phí 1 ô nhớ)
Solution 2: Dùng biến rear trỏ tới phần tử ngay sau phần tử cuối Q (khi đó, 1 ô nhớ sẽ không
được dùng tới -> lãng phí 1 ô nhớ) in the queue (one memory location will be wasted).
NGUYỄN KHÁNH PHƢƠNG
Bộ môn KHMT – ĐHBK HN
Ví dụ 5: Mô phỏng giải pháp 2
Giải pháp 2: Dùng enqueue(Q, 30)
biến rear trỏ tới
phần tử ngay sau Q đã đầy!!!
phần tử cuối Q (khi Làm thế nào để biết được
đó, 1 ô nhớ sẽ lãng Q đã đầy ?
phí vì không được ? ?
dùng tới) in
rear + 1 == front
Make front point to
Q = (10, 20) the element Q = (10, 20) Q[rear] = 30; rear++;
preceding the front Q = (10, 20, 30)
element in the
dequeue(Q) queue (onedequeue (Q) dequeue(Q)
memory location
will be wasted). Q đã rỗng!!!
? ? ? Làm thế nào để biết được Q đang rỗng ?
rear == front
front++; front++; front++;
front = 4 = maxSize Q = (30) Q = empty
wrap around: front = 0
Q = (20, 30)
Dùng giải phápô nhớ2, mộtcủa mảng sẽ bị lãng phí vì không đƣợc dùng tới!!!
Cài đặt hàng đợi Queue: dùng mảng (Array)
• Cách 2: hàng đợi Q vòng tròn,[quấn quanh] (circular queue [“wrap around”])
Giải pháp 1: Dùng biến front trỏ tới phần tử ngay trước phần tử đầu Q (khi đó, 1 ô nhớ sẽ không
được dùng tới -> lãng phí 1 ô nhớ)
Vậy với giải pháp 2: giá trị ban đầu cho biến front và rear ?
front = rear = maxSize – 1;
Giải pháp 2: Dùng biến rear trỏ tới phần tử ngay sau phần tử cuối Q (khi đó, 1 ô nhớ sẽ không
được dùng tới -> lãng phí 1 ô nhớ) in the queue (one memory location will be wasted).
Vậy với giải pháp 2, giá trị ban đầu cho biến front và rear ?
front = rear = 0;
Make front point to the element preceding the front element in the queue (one memory
location will be wasted).
Ví dụ 6: Mảng có kích thước maxSize = 4
Khởi tạo: front = rear = 0; Minh họa giải pháp 2
Queue Q rỗng
Init: front = rear = 0; enqueue(Q, 2) enqueue(Q, 3) enqueue(Q, 5) dequeue(Q)
? ?
Q[rear] = 2; Q[rear] = 3; Q[rear] = 5; Dequeue Q[front]
rear++; rear++; rear++; front++;
Q= (2, 3, 5)
Q= (2) Q= (2, 3) Q= (3, 5)
(rear + 1) % maxSize == front
dequeue(Q) enqueue(Q, 10) enqueue(Q, 20) Queue Q đầy!!!
enqueue(Q, 30) ??
? ?
ERROR: Queue đầy
dequeue Q[front] Q[rear] =10; Q[rear] =20;
rear++;
front++; rear++;
Q= (5) rear==maxSize
wrap around:rear=0 Q= (5, 10, 20)
Q= (5, 10)
Ví dụ 6: Mảng có kích thước maxSize = 4
Khởi tạo: front = rear = 0; Minh họa giải pháp 2
Queue Q rỗng
dequeue(Q) dequeue(Q) dequeue(Q)
?
Q= (5, 10, 20) Dequeue Q[front] Dequeue Q[front] Dequeue Q[front]
front++; front++; front++;
Q= (10, 20) =>front = 4 =maxSize Q empty
=> wrap around: front =0
Q= (20)
Queue Q rỗng!!!
rear == front
Giải pháp 2: Dùng biến rear trỏ tới phần tử ngay sau phần tử cuối Q (khi đó, 1 ô nhớ sẽ
không được dùng tới -> lãng phí 1 ô nhớ) in
Bài tập: Viết các hàm sau trên hàng đợi Q cho trường hợp giải pháp 2
• isEmpty(Q); hàm trả về “true” nếu hàng đợi Q đang rỗng (empty)
• isFull(Q); hàm trả về “true” nếu hàng đợi Q đang đầy (full), tức là đã sử dụng tối đa bộ nhớ dành cho hàng đợi Q;
ngược lại hàm trả về giá trị “false”
• frontQ(Q); hàm trả về phần tử đầu (front (head)) hàng đợi Q; hoặc báo lỗi error nếu Q rỗng.
• enqueue(Q,x); hàm thêm phần tử x vào phía sau (back (rear)) hàng đợi Q. Nếu trước khi thêm mà Q đã đầy, thì
không thể thêm được, cần đưa ra thông báo: Q đã đầy, không thể thêm phần tử.
• x = dequeue(Q); hàm thực hện xóa phần tử nằm đầu (front (head)) hàng đợi Q, trả về x là giá trị của phần tử này.
Nếu trước khi xóa mà hàng đợi Q đã rỗng, thì đưa ra thông báo lỗi (error).
• sizeQ(Q); hàm trả về số lượng phần tử đang có trong hàng đợi Q.
250
Ứng dụng 1: nhận dạng palindrome (recognizing palindromes)
• Định nghĩa. Ta gọi palindrome là xâu mà đọc nó từ trái qua phải cũng giống như
đọc nó từ phải qua trái.
Ví dụ: NOON, DEED, RADAR, MADAM
Able was I ere I saw Elba
• Để nhận biết một xâu cho trước có phải là palindrome hay không: ta thực hiện 2
bước sau:
– Bước 1: đưa các ký tự của nó đồng thời vào một hàng đợi và một ngăn xếp.
– Bước 2: Sau đó lần lượt loại bỏ các ký tự khỏi hàng đợi và ngăn xếp và tiến
hành so sánh:
• Nếu phát hiện sự khác nhau giữa hai ký tự, một ký tự được lấy ra từ ngăn
xếp còn ký tự kia lấy ra từ hàng đợi, thì xâu đang xét không là palindrome.
• Nếu tất cả các cặp ký tự lấy ra là trùng nhau thì xâu đang xét là palindrome.
Ví dụ 1: kiểm tra “RADAR” có phải là palindrome
Bước 1: Đẩy “RADAR” vào Queue và Stack:
Kí tự hiện tại Queue Stack
(front ở bên trái, (top ở bên trái)
rear ở bên phải)
R R R
A R A A R
D R A D D A R
A R A D A A D A R
R R A D A R R A D A R
front rear top
Ví dụ 1: kiểm tra “RADAR” có phải là palindrome
Bước 2: Xóa “RADAR” khỏi Queue và Stack:
• Dequeue lần lượt từng kí tự cho đến khi queue rỗng
• Pop lần lượt từng kí tự khỏi stack cho đến khi stack rỗng
Queue Front của Top của Stack
(front ở bên trái) Queue Stack (top ở bên trái)
R A D A R R R R A D A R
A D A R A A A D A R
D A R D D D A R
A R A A A R
R R R R
empty empty empty empty
Kết luận: xâu "RADAR" là palindrome
Ví dụ 2: phát hiện palindrome
Able was I ere I saw Elba
Ứng dụng 2: Chuyển đổi xâu số về số thập phân
Thuật toán đƣợc mô tả trong sơ đồ sau:
// Chuyển dãy chữ số trong Q thành số thập phân n
// Loại bỏ các dấu cách/trống ở đầu nếu có
do { dequeue(Q, ch)
} until ( ch != blank)
// ch lúc này chứa chữ số đầu tiên của xâu đã cho
// Tính n từ dãy chữ số trong hàng đợi
n = 0;
done = false;
do { n = 10 * n + số nguyên mà ch biểu diễn;
if (! isEmpty(Q) )
dequeue(Q,ch)
else
done = true
} until ( done || ch != digit)
// Kết quả: n chứa số thập phân cần tìm
255
Cài đặt hàng đợi Queue
• Cũng tương tự stack, ta có thể cài đặt Queue bằng 2 cách:
– Sử dụng mảng (array)
– Sử dụng danh sách liên kết (linked list)
Cài đặt hàng đợi Queue: dùng danh sách liên kết
typedef struct {
DataType element;
struct node *next;
} node;
typedef struct {
node *front;
node *rear;
} queue;
với DataType là kiểu dữ liệu của phần tử sẽ lưu trữ trong hàng đợi;
DataType cần phải được khai báo trước khi khai báo hàng đợi queue.
• Cài đặt hàng đợi sử dụng danh sách liên kết:
– Phần tử ở đầu (Front/head) hàng đợi được lưu trữ là nút đầu (head) của
danh sách liên kết, phần tử ở cuối (rear) của hàng đợi là nút cuối (tail)
của danh sách.
– Thao tác Thêm (Enqueue): thêm phần tử vào cuối danh sách.
– Thao tác Xóa (Dequeue): xóa phần tử đang ở đầu danh sách.File đính kèm:
 bai_giang_cau_truc_du_lieu_va_thuat_toan_chuong_3_cac_cau_tr.pdf
bai_giang_cau_truc_du_lieu_va_thuat_toan_chuong_3_cac_cau_tr.pdf

