Bài giảng Cấu trúc dữ liệu và giải thuật - Chương: Hàng đợi ưu tiên - Bùi Tiến Lên

HÀNG ĐỢI ƯU TIÊN
 Bùi Tiến Lên
 01/01/2017
 Dẫn nhập
 Một số ứng dụng kiểu hàng đợi thông thường không thể giải quyết
 được như
 I Sắp hàng mua vé: thường sẽ ưu tiên cho người già, phụ nữ có
 thai, người tàn tật
 I Trạm thu phí: thường ưu tiên sẽ cứu thương, xe cứu hỏa
Spring 2017 Data structure & Algorithm 2
 Hàng đợi ưu tiên
 Định nghĩa 1
 Hàng đợi ưu tiên (priority queue) là một hàng đợi trong đó mỗi
 phần tử được gắn với một con số được gọi là độ ưu tiên
 I Độ ưu tiên sẽ do ứng dụng xác định
 I Việc lấy một phần tử ra khỏi hàng đợi sẽ được dựa trên độ ưu
 tiên và quy tắc FIFO. Nghĩa là phần tử nào có độ ưu tiên cao
 nhất sẽ được lấy ra trước nhất. Trong trường hợp có nhiều
 phần tử có cùng độ ưu tiên thì sử dụng quy tắc FIFO
Spring 2017 Data structure & Algorithm 3
 Các thao tác cơ bản của hàng đợi ưu tiên
 Các thao tác đối với hàng đợi ưu tiên giống với hàng đợi bình
 thường
 I Khởi tạo hàng đợi rỗng
 I Xóa hàng đợi
 I Thêm phần tử vào hàng đợi (enqueue)
 I Lấy phần tử ở đỉnh ra khỏi hàng đợi (dequeue)
 I Lấy thông tin phần tử ở đỉnh của hàng đợi (top)
Spring 2017 Data structure & Algorithm 4
 Cài đặt hàng đợi ưu tiên
 Hàng đợi ưu tiên có thể cài đặt
 I Bằng mảng
 I Bằng cây heap
Spring 2017 Data structure & Algorithm 5
 Cấu trúc dữ liệu cây heap
 Định nghĩa 2
 I Cấu trúc dữ liệu cây heap (heap tree) là cây có thứ tự bộ
 phận. Trong phạm vi môn học chúng ta sẽ xét cây heap nhị
 phân
 I Cây max heap nhị phân là một cây nhị phân hoàn chỉnh
 sao cho giá trị khóa tại một nút bất kỳ p không nhỏ hơn khóa
 của cây con trái và cây con phải của nó
 ∀q ∈ {p → left, p → right} : q → key ≤ p → key (1)
 I Cây min heap nhị phân là một cây nhị phân hoàn chỉnh sao
 cho giá trị khóa tại một nút bất kỳ p không lớn hơn khóa của
 cây con trái và cây con phải của nó
 ∀q ∈ {p → left, p → right} : q → key ≥ p → key (2)
Spring 2017 Data structure & Algorithm 6
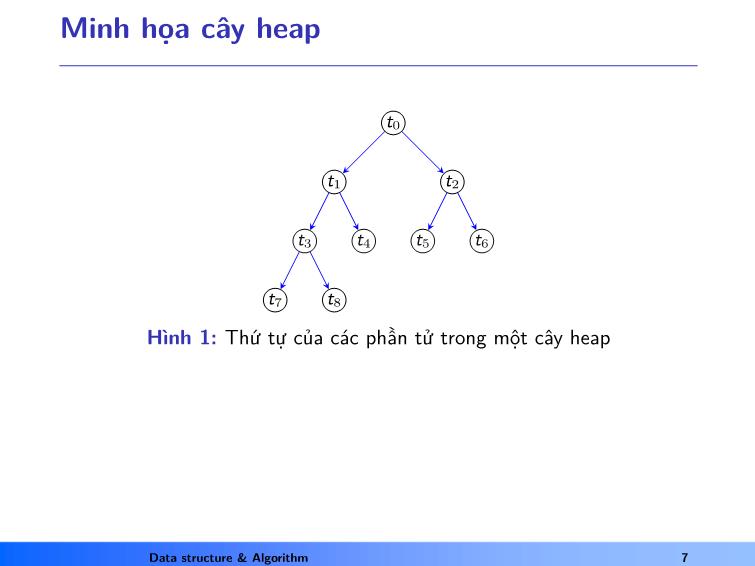
 Minh họa cây heap
 t0
 t1 t2
 t3 t4 t5 t6
 t7 t8
 Hình 1: Thứ tự của các phần tử trong một cây heap
Spring 2017 Data structure & Algorithm 7
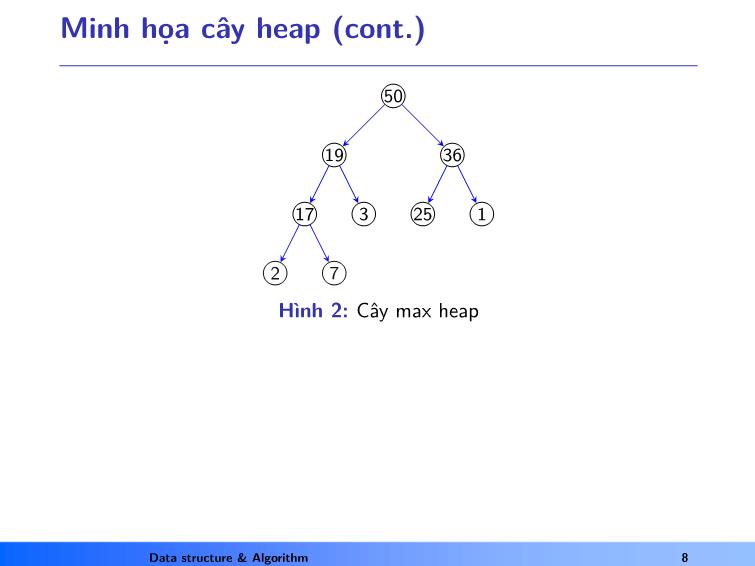
 Minh họa cây heap (cont.)
 50
 19 36
 17 3 25 1
 2 7
 Hình 2: Cây max heap
Spring 2017 Data structure & Algorithm 8
 Thao tác thêm phần tử
 Thao tác thêm một phần tử vào hàng đợi ưu tiên được cài đặt
 bằng cây max heap như sau
 I Chèn phần tử với độ ưu tiên (khóa) v vào cuối heap
 I Nếu độ ưu tiên (khóa) của nó cao hơn nút cha thì hoán đổi
 hai nút với nhau và lặp lại
Spring 2017 Data structure & Algorithm 9
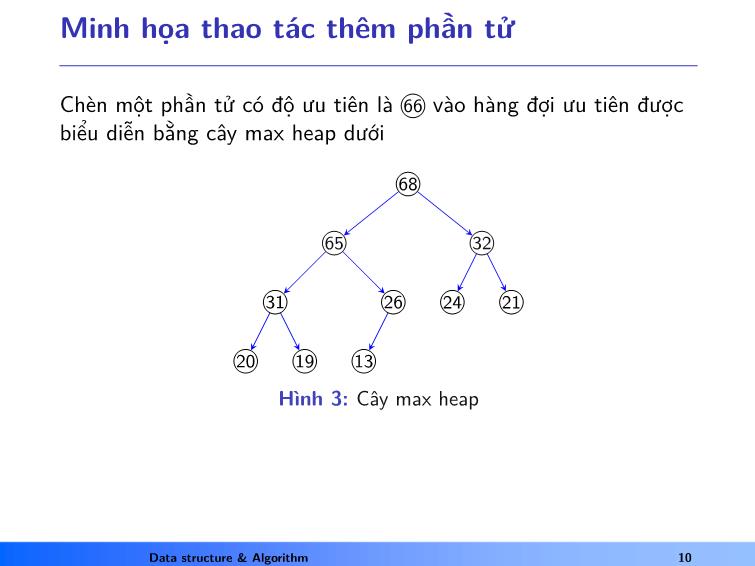
 Minh họa thao tác thêm phần tử
 Chèn một phần tử có độ ưu tiên là 66 vào hàng đợi ưu tiên được
 biểu diễn bằng cây max heap dưới
 68
 65 32
 31 26 24 21
 20 19 13
 Hình 3: Cây max heap
Spring 2017 Data structure & Algorithm 10
 Minh họa thao tác thêm phần tử (cont.)
 68
 65 32
 31 26 24 21
 20 19 13 66
 Hình 4: Thêm phần tử 66
Spring 2017 Data structure & Algorithm 11
 Minh họa thao tác thêm phần tử (cont.)
 68
 65 32
 31 66 24 21
 20 19 13 26
 Hình 5: 66 hoán đổi với 26
Spring 2017 Data structure & Algorithm 12
 Minh họa thao tác thêm phần tử (cont.)
 68
 66 32
 31 65 24 21
 20 19 13 26
 Hình 6: Hoán đổi 66 với 65
Spring 2017 Data structure & Algorithm 13
 Thao tác lấy phần tử
 Thao tác lấy một phần tử ra khỏi hàng đợi được cài đặt bằng cây
 heap như sau
 I Xóa phần tử gốc của cây heap ra khỏi cây
 I Thay thế bằng phần tử gốc bằng phần tử cuối của cây
 I Nếu độ ưu tiên của nó bằng hay thấp hơn của nút con thì
 hoán đổi nó với nút con có độ ưu tiên cao hơn
Spring 2017 Data structure & Algorithm 14
 Minh họa thao tác lấy phần tử
 Lấy phần tử gốc có độ ưu tiên cao nhất 68 khỏi cây max heap
 68
 65 32
 31 26 24 21
 20 19 13
 Hình 7: Cây max heap
Spring 2017 Data structure & Algorithm 15
 Minh họa thao tác lấy phần tử (cont.)
 xx
 65 32
 31 26 24 21
 20 19 13
 Hình 8: Xóa phần tử 68
Spring 2017 Data structure & Algorithm 16
 Minh họa thao tác lấy phần tử (cont.)
 13
 65 32
 31 26 24 21
 20 19
 Hình 9: Thay thế bằng phần tử 13
Spring 2017 Data structure & Algorithm 17
 Minh họa thao tác lấy phần tử (cont.)
 65
 13 32
 31 26 24 21
 20 19
 Hình 10: Hoán đổi 13 và 65
Spring 2017 Data structure & Algorithm 18
 Minh họa thao tác lấy phần tử (cont.)
 65
 31 32
 13 26 24 21
 20 19
 Hình 11: Hoán đổi 13 và 31
Spring 2017 Data structure & Algorithm 19
 Minh họa thao tác lấy phần tử (cont.)
 65
 31 32
 20 26 24 21
 13 19
 Hình 12: Hoán đổi 13 và 20
Spring 2017 Data structure & Algorithm 20
 Bài luyện tập
 Ví dụ 1
 Hãy xây dựng cây heap từ dãy {5, 1, 4, 3, 2, 8, 9, 7, 16, 11, 12,
 15}
 I Xóa các nút 8, 16
 I Thêm các nút 6, 17
Spring 2017 Data structure & Algorithm 21
 Đánh giá hàng đợi ưu tiên
 Cài đặt bằng mảng
 Phân tích chi phí thực hiện theo n (số lượng phần tử)
 xấu nhất trung bình tốt nhất
 tìm một phần tử ???
 thêm một phần tử ???
 xóa một phần tử ???
Spring 2017 Data structure & Algorithm 22
 Đánh giá hàng đợi ưu tiên (cont.)
 Cài đặt bằng cây heap
 Phân tích chi phí thực hiện theo n (số lượng nút)
 xấu nhất trung bình tốt nhất
 tìm một phần tử ???
 thêm một phần tử ???
 xóa một phần tử ???
Spring 2017 Data structure & Algorithm 23
 Tài liệu tham khảo
Spring 2017 Data structure & Algorithm 24