Bài giảng Cấu trúc dữ liệu và giải thuật - Chương 7: Giải thuật tìm kiếm - Ngô Công Thắng

Chương 7: Giải thuật tìm kiếm
1. Bài toán tìm kiếm
* Bài toán tìm kiếm được phát biểu như sau:
Cho một bảng gồm n bản ghi r1, r2 , . . . , rn; 
ri ( 1<= i <=n ) tương ứng với một khoá ki . 
Hãy tìm bản ghi có giá trị khoá tương ứng 
bằng x cho trước.
* Gọi x là khoá tìm kiếm hay giá trị tìm kiếm. 
Công việc tìm kiếm sẽ hoàn thành khi có 
một trong 2 tình huống sau xảy ra:
1- Tìm được bản ghi có giá trị khoá tương 
ứng bằng x. Lúc đó ta nói phép tìm kiếm 
được thoả. 
2- Không tìm được bản ghi nào có giá trị 
khoá bằng x . Khi đó ta nói phép tìm kiếm 
không thoả.
Sau phép tìm kiếm không thoả nếu có yêu 
cần bổ sung bản ghi mới có khoá x vào
bảng. Giải thuật này gọi là “ Tìm kiếm có bổ 
sung”.
Khoá của mỗi bản ghi chính là đặc điểm 
nhận biết của bản ghi đó trong tìm kiếm, ta 
coi nó là đại diện của bản ghi trong giải 
thuật.
2. Tìm kiếm tuần tự ( Sequential searching )
2.1. Phương pháp
Đây là giải thuật đơn giản, cổ điển.
Cách thức làm như sau: Bắt đầu từ bản ghi thứ 
nhất, lần lượt so sánh khoá tìm kiếm với tương 
ứng của các bản ghi trong bảng cho đến khi tìm 
thấy bản ghi mong muốn hoặc đã hết danh sách 
mà chưa thấy.
* Giải thuật:
Cho dãy khoá K có n phần tử. Tìm xem có khoá 
nào bằng x, nếu có đưa ra thứ tự của khoá đó, 
nếu không có thì đưa ra giá trị 0. Trong giải thuật 
sử dụng khoá phụ kn+1=x.
Function SequenceSearch(k,n,x)
1. { Khởi đầu }
i:=1; k[n+1]:=x;
2. {Tìm kiếm trong dãy}
While k[i] x Do i:=i+1;
3. { Không tìm thấy }
If i=n+1 then Return(0) Esle Return(i);
Return
3. Tìm kiếm nhị phân (Binary searching )
3.1 Phương pháp
* Phương pháp tìm kiếm thực hiện trên dãy
khóa đã sắp xếp, có nội dung như sau:
- Tương tự như tra tìm từ trong từ điển hoặc
danh bạ điện thoại. Chỉ khác là trong tra cứu
ta chọn từ ngẫu nhiên, còn trong tìm kiếm
nhị phân luôn chọn khoá “ở giữa” dẫy khoá.
- Giả sử có dãy khoá kL, . . ., kR thì khoá ở 
giữa là km với
m=(L+R) div 2
+ Tìm kiếm sẽ kết thúc nếu: x=km
+ Nếu x<km tìm kiếm sẽ được thực hiện 
tiếp với kL, . . . , km-1 với cách tương 
tự.
+ Nếu x>km tìm kiếm sẽ được thực hiện 
tiếp với km+1, . . . , kR với cách tương 
tự.
Qúa trình tìm kiếm kết thúc khi tìm thấy 
một khoá mong muốn hoặc dãy khoá 
rỗng (không tìm thấy ).
* Giải thuật:
Cho dãy K gồm n khoá, sắp xếp theo thứ tự tăng dần. Tìm 
khoá có giá trị =x.
Dùng biến L, R, m: chỉ số đầu, chỉ số cuối, chỉ số giữa của 
khoá k.
Nếu tìm thấy cho ra chỉ số của khoá đó, nếu không tìm thấy 
cho ra 0.
Function BinarySearch(K,n,x)
1. { Khởi tạo }
L:=1; R:=n;
2. { Tìm kiếm }
While L<= R Do
Begin
3. { Tính chỉ số giữa }
m:=( L+R) div 2;
4. { So sánh }
If x<k[m] then R:=m-1
Else IF x>k[m] then L:=m+1
Else Return (m);
End; {End of While}
5. { Không tìm thấy }
Return (0)
* Giải thuật viết dạng đệ quy như sau:
L, r là chỉ số đầu, chỉ số cuối của dãy K, biến 
nguyên Loc để đưa ra chỉ số ứng với khoá cần 
tìm, nếu không tìm thấy thì Loc =0.
Function BinarySearch(L,R,x)
If L>R then Loc:=0
Else 
begin m:=(L+R) div 2;
If x<k[m] then 
Loc:=BinarySearch(L,m-1,x)
Else If x>k[m] then 
Loc:=BinarySearch(m+1,R,x)
Else Loc:=m;
end;
Return(Loc)
3.2. Đánh giá
Phép tính tích cực là phép so sánh L<= r
Cmin=1
Người ta đã tính được 
Cmax=[log2n ]
Ttb=O(log2n )
Tìm kiếm nhị phân tốt hơn tìm kiếm 
tuần tự nhưng dãy k phải được sắp.
4. Cây nhị phân tìm kiếm
4.1. Định nghĩa cây nhị phân tìm kiếm
* Cây nhị phân tìm kiếm ứng với n khoá k1, k2, ..., kn
là một cây nhị phân mà mỗi nút của nó đều được 
định danh bởi một khoá nào đó trong các khoá đã 
cho. Đối với mọi nút trên cây tính chất sau đây 
luôn được thoả mãn:
- Mọi khoá thuộc cây con trái của một nút đều nhỏ
hơn khoá ứng với nút đó.
- Mọi khoá thuộc cây con phải của một nút đều lớn 
hơn khoá ứng với nút đó.
Chú ý : Khoá là số thì so sánh số bình thường, 
Khoá là chữ thì ta so sánh xâu kí tự.
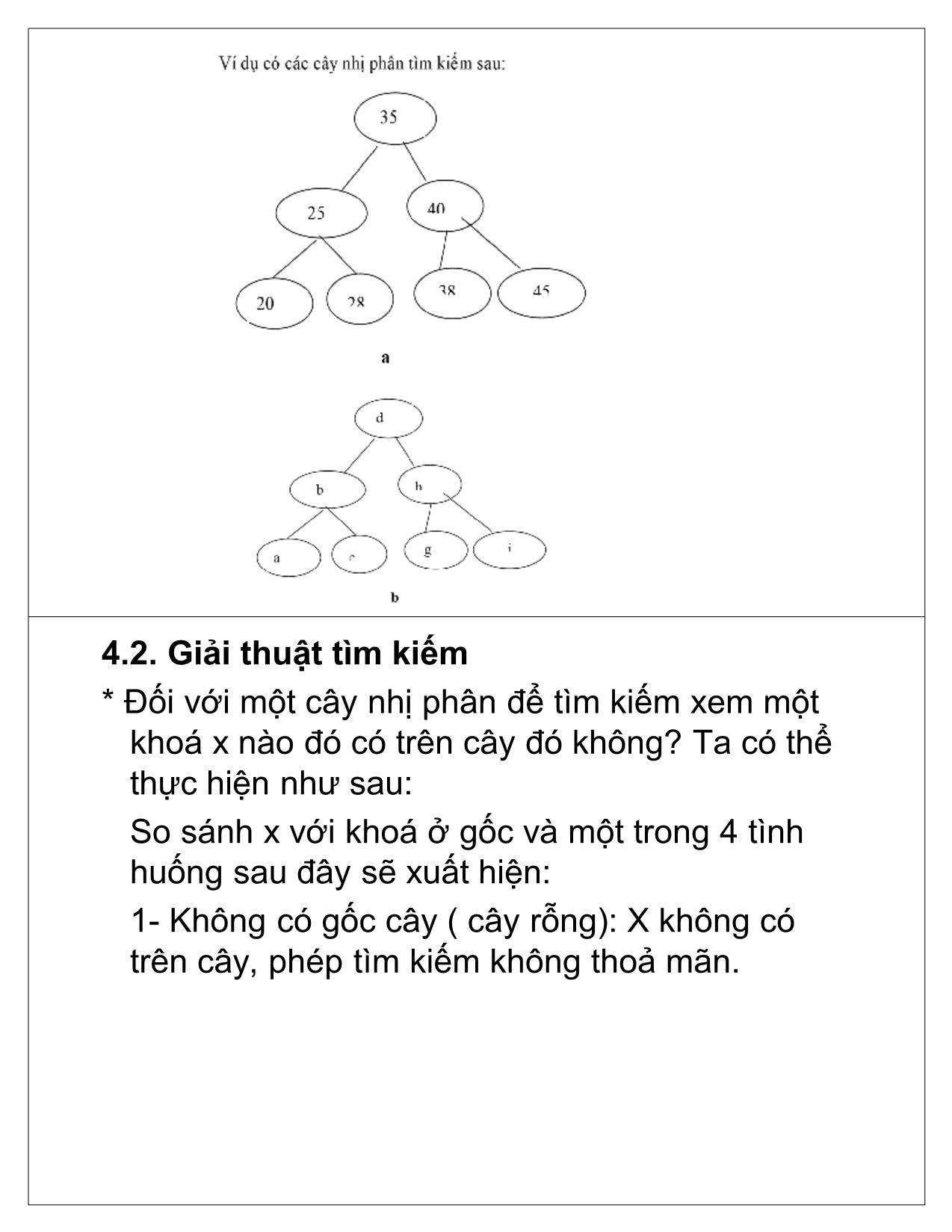
4.2. Giải thuật tìm kiếm
* Đối với một cây nhị phân để tìm kiếm xem một 
khoá x nào đó có trên cây đó không? Ta có thể 
thực hiện như sau:
So sánh x với khoá ở gốc và một trong 4 tình 
huống sau đây sẽ xuất hiện:
1- Không có gốc cây ( cây rỗng): X không có 
trên cây, phép tìm kiếm không thoả mãn.
2- X trùng với khoá ở gốc: Phép tìm kiếm 
được thoả mãn.
3- X nhỏ hơn khoá ở gốc: Tìm kiếm được 
thực hiện tiếp tục bằng cách xét cây con trái 
của gốc với cách làm tương tự.
4- X lớn hơn khoá ở gốc: Tìm kiếm được 
thực hiện tiếp tục bằng cách xét cây con 
phải của gốc với cách làm tương tự.
Ví dụ Tìm x=28 trên cây a: So x và 35, x<35 
nên ta tìm trên cây con trái của 35
X>25 nên lại tìm trong cây con phải. So sánh 
ta có x=cây con phải cũng là 28 nên phép 
tìm kiếm được thoả mãn.
Bài tập chương 8
Bài 1: Cho 1 dãy số a1, a2, ..., an. Hãy tìm phần tử bằng 
giá trị x nhập vào từ bàn phím. Lập trình theo 3 cách 
tìm kiếm nêu trên: tìm kiếm tuần tự, tìm kiếm nhị 
phân, cây nhị phân tìm kiếm.
Bài 2: Cho 1 danh sách điểm của sinh viên. Mỗi bản ghi 
gồm các trường: Họ tên, số báo danh, điểm thi. Hãy 
tìm sinh viên có số báo danh bằng giá trị x nhập vào 
từ bàn phím. Lập trình theo 3 cách tìm kiếm nêu 
trên:tìm kiếm tuần tự, tìm kiếm nhị phân, cây nhị phân 
tìm kiếm.