Bài giảng Cấu trúc dữ liệu và giải thuật - Chương 5: Đồ thị - Ngô Công Thắng
1. Các khái niệm
1.1. Định nghĩa đồ thị
Đồ thị G(V,E) bao gồm một tập hữu hạn V các đỉnh
(hay nút) và một tập hữu hạn E các cặp đỉnh mà ta
gọi là cung ( hay cạnh).
Ví dụ 1: Một mạng gồm các máy tính và các kênh điện
thoại nối các máy tính này là một đồ thị.
Ví dụ 2: Một mạng gồm các thành phố, thị xã và các
đường bộ nối các thành phố, thị xã là một đồ thị.
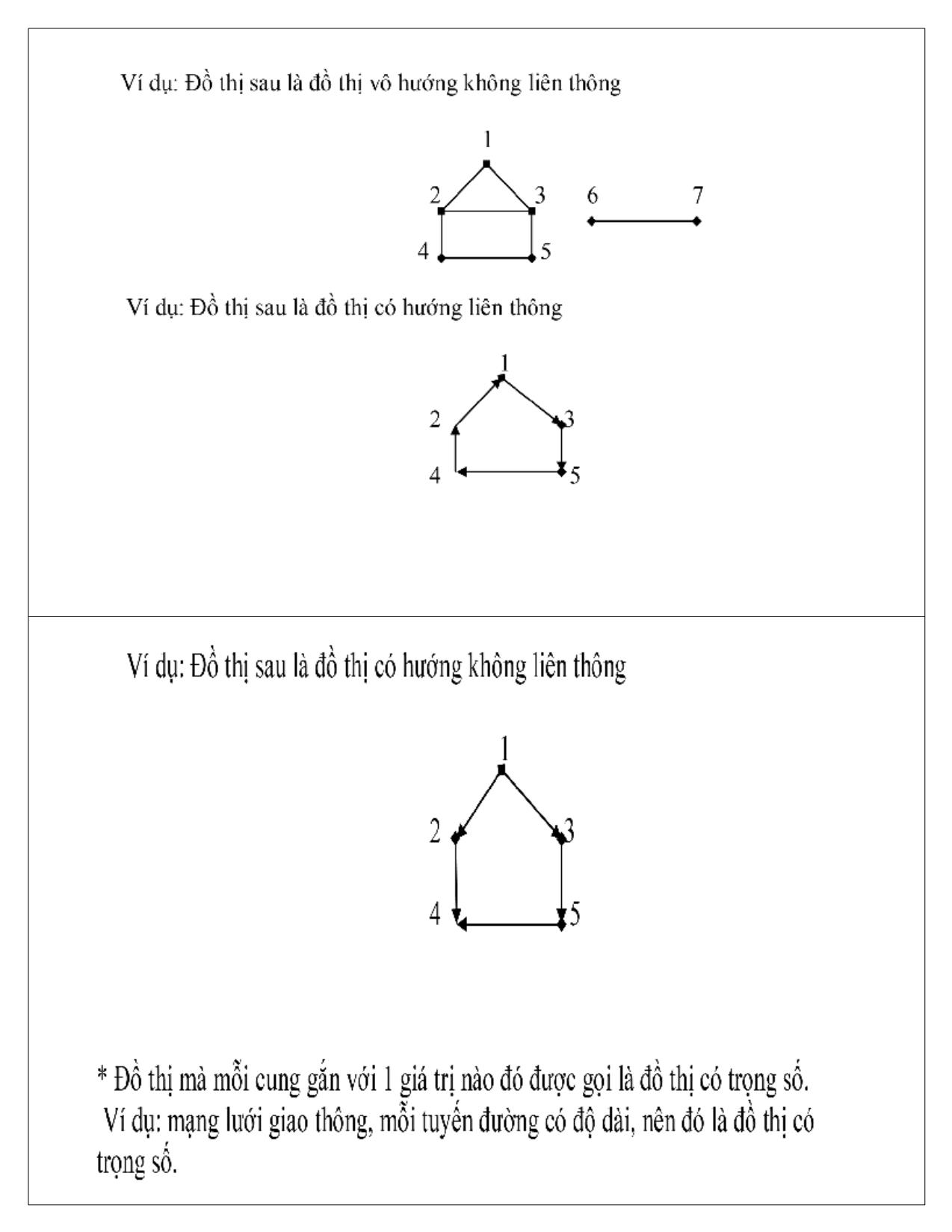
1.2. Định nghĩa đồ thị vô hướng
Đồ thị vô hướng G=(V,E) bao gồm V là tập các đỉnh và
E là tập các cặp đỉnh không có thứ tự gọi là các cung.

Trang 1

Trang 2
Trang 3

Trang 4

Trang 5

Trang 6
Trang 7

Trang 8

Trang 9
Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Cấu trúc dữ liệu và giải thuật - Chương 5: Đồ thị - Ngô Công Thắng", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Cấu trúc dữ liệu và giải thuật - Chương 5: Đồ thị - Ngô Công Thắng

Chương 5: Đồ thị
1. Các khái niệm
1.1. Định nghĩa đồ thị
Đồ thị G(V,E) bao gồm một tập hữu hạn V các đỉnh
(hay nút) và một tập hữu hạn E các cặp đỉnh mà ta
gọi là cung ( hay cạnh).
Ví dụ 1: Một mạng gồm các máy tính và các kênh điện
thoại nối các máy tính này là một đồ thị.
Ví dụ 2: Một mạng gồm các thành phố, thị xã và các
đường bộ nối các thành phố, thị xã là một đồ thị.
1.2. Định nghĩa đồ thị vô hướng
Đồ thị vô hướng G=(V,E) bao gồm V là tập các đỉnh và
E là tập các cặp đỉnh không có thứ tự gọi là các cung.
* Nếu (v1, v2) là một cung trong tập E(G) thì v1 và v2 gọi là lân
cận của nhau.
Ví dụ trên 1,2 là lân cân, 1,3 là lân cận.
* Một đường đi từ đỉnh u đến đỉnh v trong đồ thị là một dãy các
đỉnh
u=x0, x1, ..., xn-1, xn=v mà dãy các cạnh (x0, x1), (x1, x2), ...,
(xn-1, xn) là các cung thuộc E(G) .
* Số lượng cung trên đường đi gọi là độ dài của đường đi.
Ví dụ đường đi từ 1 đến 4 có độ dài là 2.
* Đường đi đơn: Là đường đi mà mọi đỉnh trên đó, trừ đỉnh đầu và
đỉnh cuối đều khác nhau.
* Một chu trình là một đường đi đơn mà đỉnh đầu và đỉnh cuối
trùng nhau.
Ví dụ: 1→ 3 → 5→ 4→1
3. Phép duyệt đồ thị
* Xét đồ thị vô hướng G(V,E) và một đỉnh vÎV. Ta cần thăm tất cả các
đỉnh của G mà có thể “ với tới” từ đỉnh v ( nghĩa là đồ thị liên thông).
Có 2 cách duyệt đồ thị:
- Phép tìm kiếm theo chiều sâu ( Depth first search )
- Phép tìm kiếm theo chiều rộng (Breadth first search )
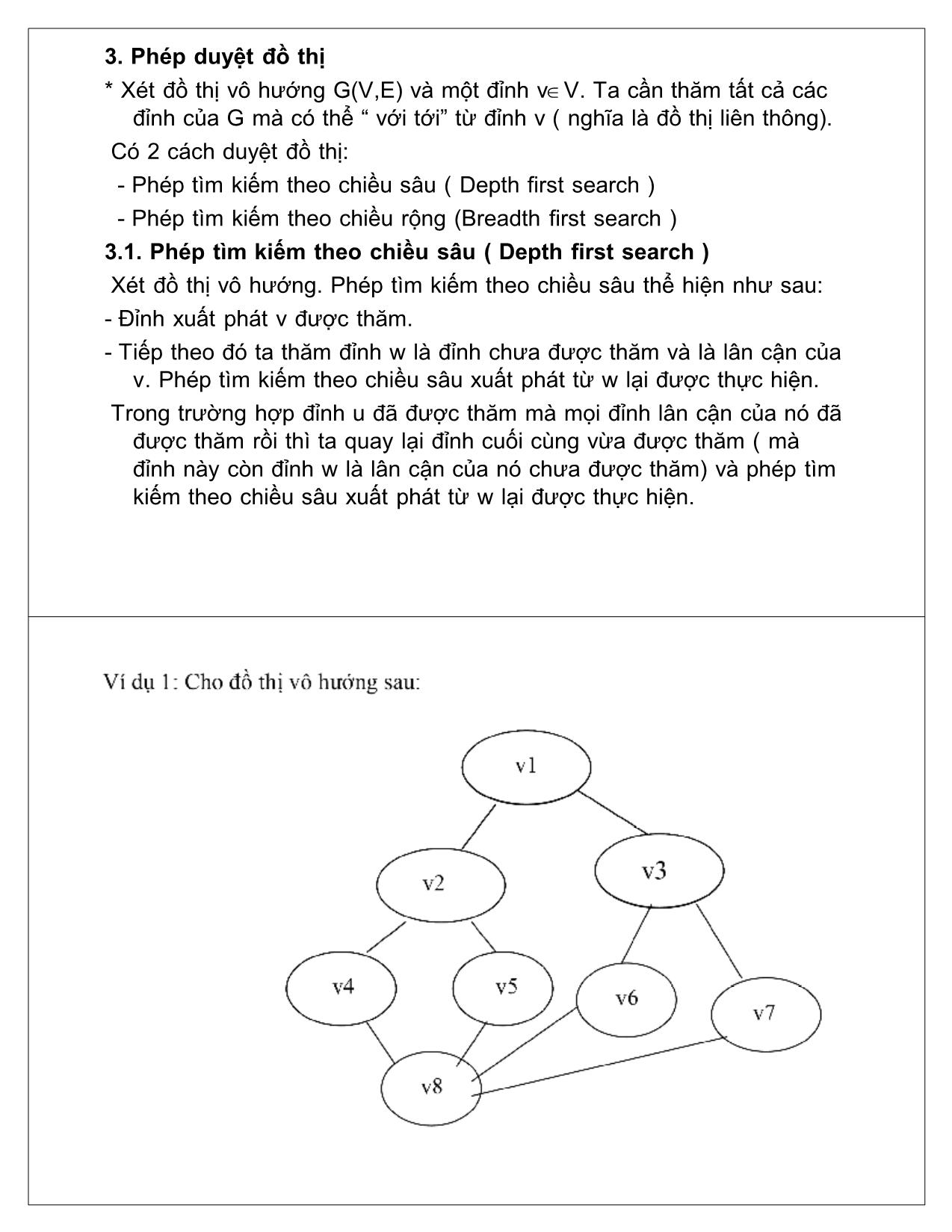
3.1. Phép tìm kiếm theo chiều sâu ( Depth first search )
Xét đồ thị vô hướng. Phép tìm kiếm theo chiều sâu thể hiện như sau:
- Đỉnh xuất phát v được thăm.
- Tiếp theo đó ta thăm đỉnh w là đỉnh chưa được thăm và là lân cận của
v. Phép tìm kiếm theo chiều sâu xuất phát từ w lại được thực hiện.
Trong trường hợp đỉnh u đã được thăm mà mọi đỉnh lân cận của nó đã
được thăm rồi thì ta quay lại đỉnh cuối cùng vừa được thăm ( mà
đỉnh này còn đỉnh w là lân cận của nó chưa được thăm) và phép tìm
kiếm theo chiều sâu xuất phát từ w lại được thực hiện.
Phép duyệt theo chiều sâu đi theo trình tự sau:
v1 ® v2 ® v4 ® v8 ® v5 ® v6 ® v3 ® v7
* Thủ tục phép duyệt theo chiều sâu như sau:
Cho một đồ thị G(V,E) vô hướng có n đỉnh và véc tơ Visited(n) gồm n phần tử,
ban đầu véc tơ này có giá trị =0. Thuật giải này thực hiện thăm mọi đỉnh “
với tới được “ từ đỉnh v.
Procedure DFS(v)
1) Visited[v]:=1; { đánh dấu v được thăm }
2) Write(v); {Đưa ra đỉnh v}
3) FOR mỗi đỉnh w lân cận với v DO
If Visited[w] = 0 then CALL DFS(w);
Return
* Đánh giá thuật toán:
+ Trường hợp biểu diễn đồ thị dùng danh sách móc nối: G có e cung, mỗi
nút với tới 1 lần, nên thời gian tìm kiếm là O(e).
+ Trường hợp biểu diễn đồ thị dùng ma trận lân cận : thì thời gian xác
định mọi điểm lân cận của v là O(n). Có n đỉnh nên thời gian tìm kiếm là
O(n2).
3.2. Phép tìm kiếm theo chiều rộng (Breadth first search )
Xét đồ thị vô hướng. Phép tìm kiếm theo chiều rộng thể hiện
như sau:
- Đỉnh xuất phát v được thăm.
- Tiếp theo các đỉnh chưa được thăm mà là lân cận của v sẽ
được thăm, rồi đến các đỉnh chưa được thăm là lân cận làn
lượt của các đỉnh này và cứ tương tự như vậy.
Ví dụ 1 ở trên: Phép duyệt theo chiều rông đi theo trình tự sau:
v1 ® v2 ® v3 ® v4 ® v5 ® v6 ® v7 ® v8
* Thủ tục phép duyệt theo chiều rong như sau:
Cho một đồ thị G(V,E) vô hướng có n đỉnh và véc tơ Visited(n)
gồm n phần tử, ban đầu véc tơ này có giá trị =0. Thuật giải này
thực hiện thăm mọi đỉnh “ với tới được “ từ đỉnh v. Bắt đầu từ
đỉnh v. Mọi đỉnh i được thăm đánh dấu bằng Visited(i):=1.
Dùng hàng đợi Q có kích thước n; F, R là lối trước và lối sau của
hàng đợi. Khi thăm 1 đình thì loại bỏ khỏi hàng đợi; khi chưa
thăm thì bổ sung vào hàng đợi
Procedure BFS(v)
1) Khởi tạo hàng đợi Q với v được đưa vào.
2) Visited[v]:=1; { đánh dấu v được thăm }
3) Write(v); {Đưa ra v}
4) While Q không rỗng DO
Begin
Call CQDELETE(v,Q) { loại bỏ v ra khỏi Q}
FOR mỗi đỉnh w lân cận với v DO
Begin
If Visited[w]=0 then
Begin
Visited[w]:=1; Write(w);
CALL CQINSERT(w,Q); { Bổ sung w vào Q}
End
End
End
Return
* Đánh giá giải thuật: Vòng lặp While lặp lại n lần .
- Nếu biểu diễn đồ thị bằng ma trận lân cận thì thời gian thực
hiện là O(n2).
- Nếu biểu diễn đồ thị bằng danh sách lân cận thì thời gian thực
hiện là O(e).
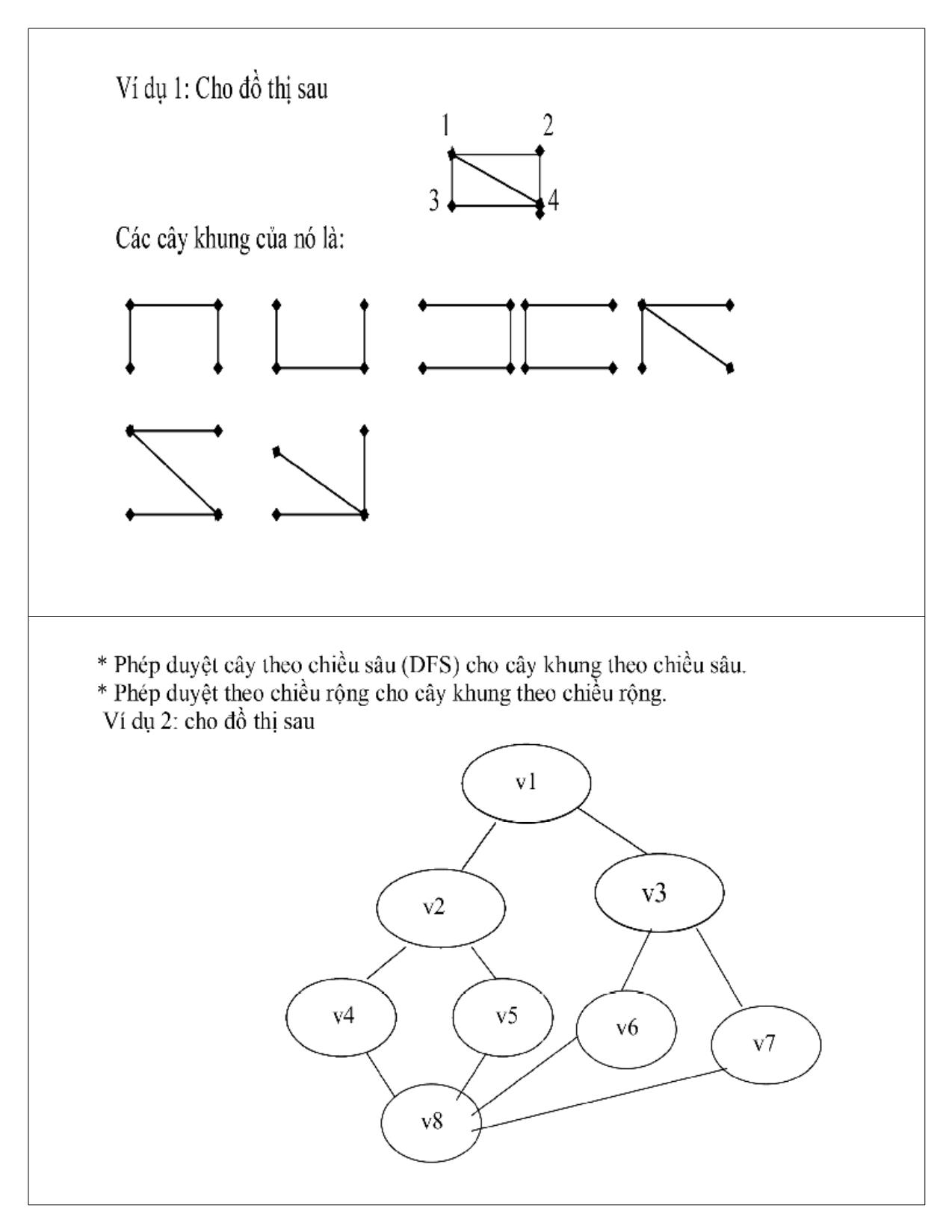
4. Cây khung và cây khung với giá trị cực tiểu
4.1. Cây khung
* Nếu G là đồ thị liên thông thì phép tìm kiếm theo chiều sâu hoặc
theo chiều rộng xuất phát từ 1 đỉnh thăm mọi đỉnh. Như vậy các
cung trong G phân thành 2 tập:
- Tập T chứa các cung đã được duyệt qua.
- Tập b gồm các cung còn lại.
* Tất cả các cung và các đỉnh trong T sẽ tạo thành một cây con
bao gồm mọi đỉnh của G. Cây con như vậy gọi là cây khung
của G.
4.2. Cây khung với giá trị cực tiểu
* Bài toán: Xác định cây khung với giá trị cực tiểu của đồ thị liên
thông có trọng số.
Gía trị của cây khung là tổng các trọng số ứng với các cạnh của
cây khung.
* Có nhiều giải thuật xác định cây khung với giá trị cực tiểu nhưng
trong phần này ta chỉ xét giải thuật Kruskal. Với giải thuật này
cây khung T sẽ được xây dựng dần từng cung một. Các cung
đưa vào T thoả mãn:
- Cung có giá trị cực tiểu trong các cung còn lại.
- Không tạo ra chu trình với các cung đã có của T.
* Giải thuật Kruskal được viết như sau:
1. T=F { T rỗng
2. While T chứa ít hơn (n-1) cung Do
3. Begin Chọn 1 cung (v,w) từ E có giá trị nhỏ nhất.
4. Loại (v,w) ra khỏi E
5. If (v,w) không tạo nên chu trình trong T Then
đưa (v,w) vào T.
End;
6. Return
* Đánh giá giải thuật:
Thời gian thực hiện giải thuật xác định qua thực hiện
bước 3 và 4.
Trường hợp xấu nhất sẽ là O(e.log e) trong đó e là số
cung của đồ thị G.
5. Bài toán tìm đường đi ngắn nhất
( Bài toán một nguồn mọi đích)
( Single source all destination )
* Cho đồ thị có hướng G(V,E), một hàm trọng số w(e)
cho các cung e của G và một đỉnh nguồn v0 .
Bài toán đặt ra là: Xác định đường đi ngắn nhất từ v0
đến mọi đỉnh còn lại của G ( độ dài đường đi là tổng
các trọng số trên các cung đường đi đó và các trọng
số đều dương )
* Gọi S là tập các đỉnh kể cả v0 mà đường đi ngắn nhất
xác lập.
Đối với 1 đỉnh w Î S, gọi Dist(w) là độ dài của đường
đi ngắn nhất từ v0 qua các đỉnh trong S và kết thúc ở
w thì sẽ có một số nhận xét sau:
1. Nếu đường đi ngắn nhất tới w thì đường đi đó bắt
đầu từ v0 kết thúc ở w và chỉ đi qua những đỉnh thuộc
S.
2. Đích của đường đi sinh ra tiếp theo phải là một đỉnh
w nào đó Ï S mà có Dist(w) ngắn nhất so với mọi đỉnh
Ï S .
3. Nếu đã chọn được một đỉnh w như trong nhận xét 2
ở trên và sinh ra một đường đi ngắn nhất từ v0 đến w
thì w sẽ trở thành 1 phần tử của S.
* Dưa trên các quan điểm như các nhận xét nêu trên Diskstra đưa ra giải thuật
tìm đường đi ngắn nhất như sau:
- Giả thiết n đỉnh của G được đánh số từ 1 tới n.
- Tập S được thể hiện bằng véc tơ bít: S[i] = 0 nếu đỉnh i Ï S
S[i] = 1 nếu đỉnh i ÎS
- Độ dài trọng số biểu diễn bằng ma trận lân cận Cost:
Cost[i,j] là trọng số cung (i,j)
Cost[i,j] = + ¥ nếu cung (i,j) không có.
Cost[i,j] = 0 nếu i=j
Ví dụ trên thì ma trận lân cân Cost như sau:
v0 v1 v2 v3 v4 v5
v0 0 50 10 + ¥ 45 + ¥
v1 + ¥ 0 15 + ¥ 10 + ¥
v2 20 + ¥ 0 15 + ¥ + ¥
v3 + ¥ 20 + ¥ 0 35 + ¥
v4 + ¥ + ¥ + ¥ 30 0 + ¥
v5 + ¥ + ¥ + ¥ 3 + ¥ 0
* Giải thuật:
Procedure Shortest_Path(v,Cost,Dist,n)
{ Dist(j) 1<= j <=n là độ dài đường đi ngắn nhất từ v đến j trong đồ thị có
hướng G có n đỉnh, Dist(v)=0. G được biểu diễn bởi ma trận lân cận Cost có
kích thước n x n. }
1. For i:=1 To n Do Begin
S[i]:=0; Dist[i]:= Cost[v,i];
End;
2. S[v]:=1; Dist[v]:=0; k:=1; { đưa v vào S }
3. While k<n { xác định n-1 đường đi từ đỉnh v }
4. Begin
Chọn u sao cho Dist[u]= min(Dist[i])) với S[i]=0;
5. S[u]:=1; k:=k+1; { đưa u vào S}
6. For mọi w với S[w]=0 Do
7. Dist[w]:= min(Dist[w], Dist[u]+Cost[u,w]) { tính lại khoảng cách theo
đường đi ngắn nhất }
End;
8. Return
Bài tập
1. Nêu khái niệm đồ thị, đồ thị vô hướng, đồ thị có hướng, đường
đi, cây khung, cây khung với gía trị cực tiểu.
2. Cho đồ thị sau đây.
a- Hãy biễu diễn đồ thị bằng ma trận lân cận, bằng danh sách
lân cận
b- Duyệt đồ thị theo chiều sâu, duyệt đồ thị theo chiều rộng.
c- Tìm cây khung theo chiều sâu, cây khung theo chiều rộng.
d-Tìm cây khung với giá trị cực tiểu.
e- Viết chương trình trong Pascal tìm cây khung với giá trị cực
tiểu.
File đính kèm:
 bai_giang_cau_truc_du_lieu_va_giai_thuat_chuong_5_do_thi_ngo.pdf
bai_giang_cau_truc_du_lieu_va_giai_thuat_chuong_5_do_thi_ngo.pdf

