Bài giảng Cấu trúc dữ liệu và giải thuật - Bài: Độ tăng của hàm - Văn Chí Nam

 33
  Big-O.
  Một số kết quả Big-O quan trọng.
 Cấu trúc dữ liệu và giải thuật - HCMUS 2016
 34
  Khái niệm Big-O lần đầu tiên được đưa ra bởi nhà 
 toán học người Đức Paul Bachmann vào năm 
 1892.
  Big-O được trở nên phổ biến hơn nhờ nhà toán học 
 Landau. Do vậy, Big-O cũng còn được gọi là ký 
 hiệu Landau, hay Bachmann-Landau.
  Donald Knuth được xem là người đầu tiên truyền 
 bá khái niệm Big-O trong tin học từ những năm 
 1970. Ông cũng là người đưa ra các khái niệm Big-
 Omega và Big-Theta.
 Cấu trúc dữ liệu và giải thuật - HCMUS 2016
-HCMUS ©FIT 1
 35
  Cho f và g là hai hàm số từ tập các số nguyên 
 hoặc số thực đến số thực. Ta nói f(x) là O(g(x)) 
 nếu tồn tại hằng số C và k sao cho:
 |f(x)| ≤ C |g(x)| với mọi x > k
 Cấu trúc dữ liệu và giải thuật - HCMUS 2016
 36
  Cho f và g là hai hàm số từ tập các số nguyên 
 hoặc số thực đến số thực. Ta nói f(x) là O(g(x)) 
 nếu tồn tại hằng số C và k sao cho:
 |f(x)| ≤ C |g(x)| với mọi x > k
 • Ví dụ, hàm f(x) = x2 + 3x + 2 là O(x2).
 Thật vậy, khi x > 2 thì x < x2 và 2 < 2x2
 Do đó x2 + 3x + 2 < 6x2. 
 Nghĩa là ta chọn được C = 6 và k = 2.
 Cấu trúc dữ liệu và giải thuật - HCMUS 2016
-HCMUS ©FIT 2
 37
  Big-O giúp xác định được mối quan hệ giữa 
 f(x) và g(x), trong đó g(x) thường là hàm ta đã 
 biết trước. Từ đó ta xác định được sự tăng 
 trưởng của hàm f(x) cần khảo sát.
  C và k trong định nghĩa của khái niệm Big-O 
 được gọi là bằng chứng của mối quan hệ f(x) 
 là O(g(x)).
 Cấu trúc dữ liệu và giải thuật - HCMUS 2016
 38
  Big-O phân hoạch được các hàm với các độ 
 tăng khác nhau. Nếu có hai hàm f(x) và g(x) sao 
 cho f(x) là O(g(x)) và g(x) là O(f(x)) thì ta nói hai 
 hàm f(x) và g(x) đó là có cùng bậc.
 2 2
  Ví dụ: f(x) 7x là O(x ) (chọn k = 0, C = 7).
 Do vậy 7x2 và x2 + 3x + 2, và x2 là 3 hàm có 
 cùng bậc.
 Cấu trúc dữ liệu và giải thuật - HCMUS 2016
-HCMUS ©FIT 3
 39
 2 3 3
  Lưu ý: 7x cũng là O(x ) nhưng x không là 
 O(7x2). 
 Thật vậy: Nếu x3 là O(7x2) thì ta phải tìm được C 
 và k sao cho 
 |x3| ≤ C|7x2| x ≤ 7C với mọi x > k. 
 Điều này không thể xảy ra vì không thể tìm 
 được k và C nào như vậy.
  Do vậy, trong quan hệ f(x) là O(g(x)), hàm g(x) 
 thường được chọn là nhỏ nhất có thể.
 Cấu trúc dữ liệu và giải thuật - HCMUS 2016
 40
 1. Hàm đa thức:
 n n-1
 f(x) = anx + an-1x +  + a1x + a0
 Khi đó f(x) là O(xn).
 Cấu trúc dữ liệu và giải thuật - HCMUS 2016
-HCMUS ©FIT 4
 41
  Nếu f(x) là O(g(x)) thì c.f(x) là O(g(x)) với c là
 hằng số.
  Cho f1(x) là O(g1(x)) và f2(x) là O(g2(x)).
 Khi đó:
  Quy tắc tổng:
 (f1(x)+f2(x)) là O(max(|g1(x)|, |g2(x)|))
  Quy tắc nhân:
 (f1(x) * f2(x)) là O(g1(x) * g2(x)).
 Cấu trúc dữ liệu và giải thuật - HCMUS 2016
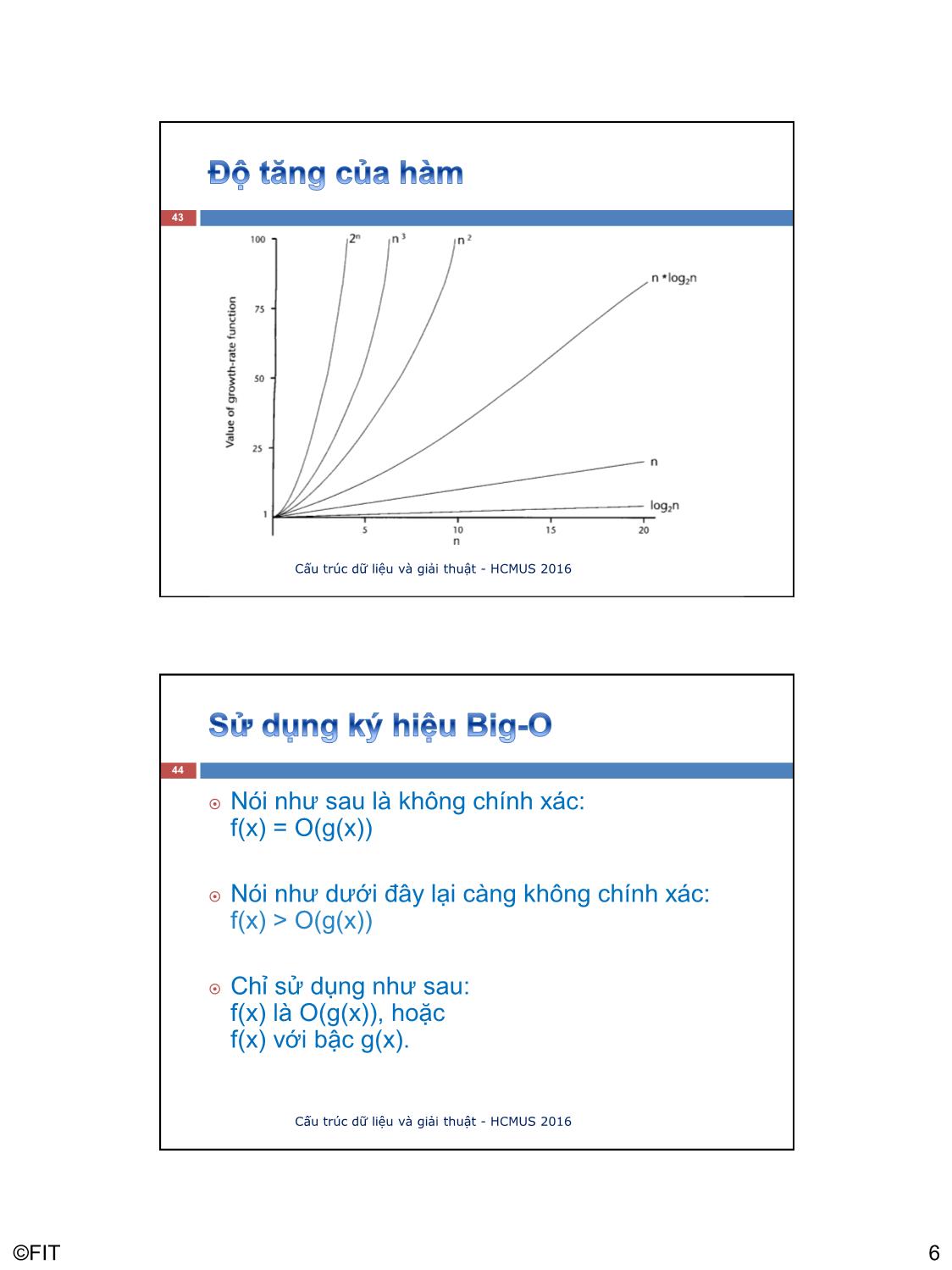
 42
 Cấu trúc dữ liệu và giải thuật - HCMUS 2016
-HCMUS ©FIT 5
 43
 Cấu trúc dữ liệu và giải thuật - HCMUS 2016
 44
  Nói như sau là không chính xác:
 f(x) = O(g(x))
  Nói như dưới đây lại càng không chính xác:
 f(x) > O(g(x))
  Chỉ sử dụng như sau:
 f(x) là O(g(x)), hoặc
 f(x) với bậc g(x).
 Cấu trúc dữ liệu và giải thuật - HCMUS 2016
-HCMUS ©FIT 6
 45
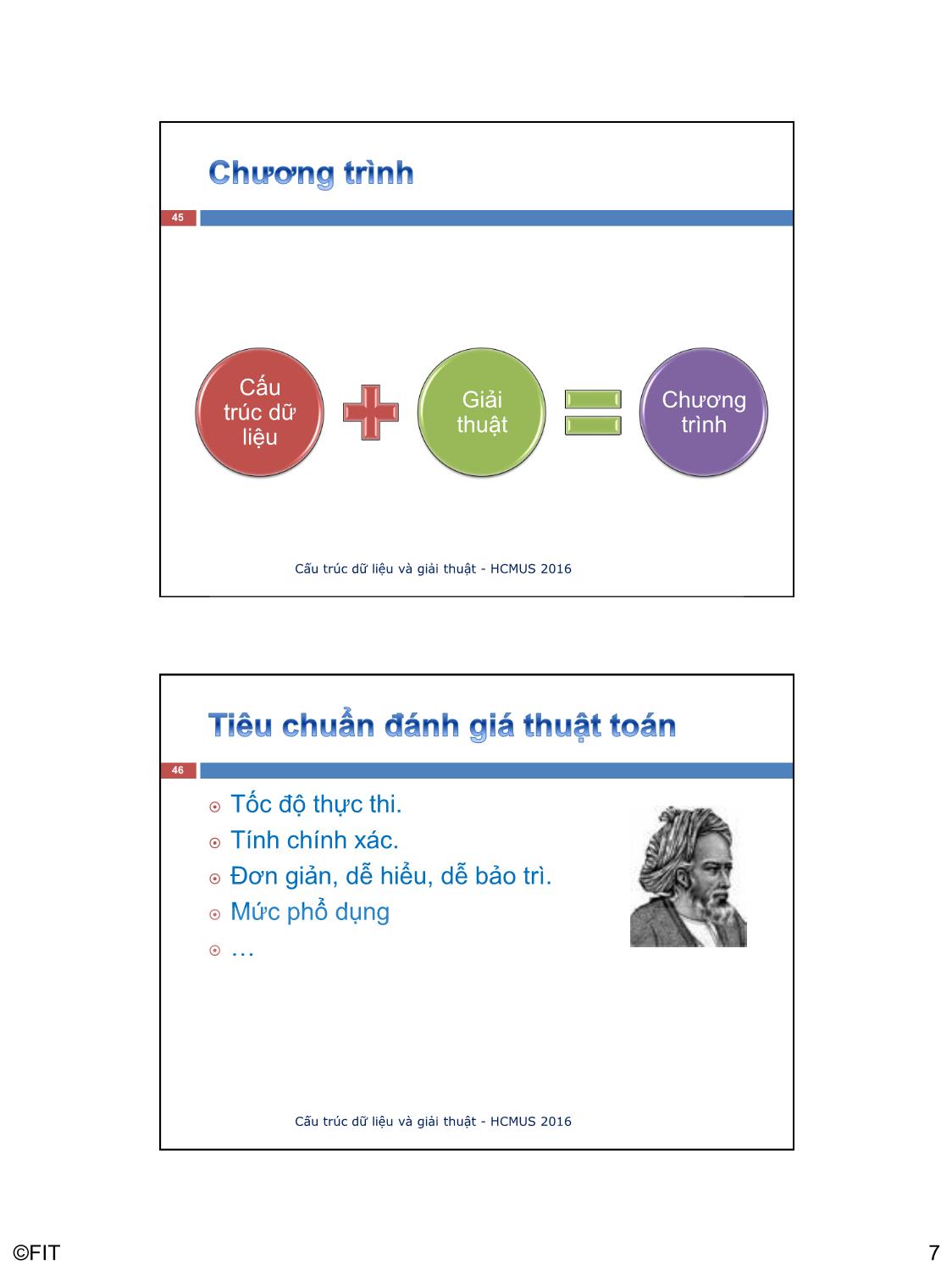
 Cấu 
 Giải Chương 
 trúc dữ 
 thuật trình
 liệu
 Cấu trúc dữ liệu và giải thuật - HCMUS 2016
 46
  Tốc độ thực thi.
  Tính chính xác.
  Đơn giản, dễ hiểu, dễ bảo trì.
  Mức phổ dụng
  
 Cấu trúc dữ liệu và giải thuật - HCMUS 2016
-HCMUS ©FIT 7
 47
  Thời gian giải quyết một bài toán phụ thuộc vào 
 nhiều yếu tố:
  Tốc độ thực thi của máy tính (phần cứng lẫn 
 phần mềm).
  Tài nguyên (ví dụ: bộ nhớ).
  Thuật toán.
  Làm thế nào đánh giá được thời gian thực thi 
 hiệu quả?
 Cấu trúc dữ liệu và giải thuật - HCMUS 2016
 48
  Đánh giá thời gian thực hiện dựa trên những 
 phép toán quan trọng như:
  Phép so sánh
  Phép gán
  Đánh giá bằng cách tính số lượng các phép 
 toán quan trọng theo độ lớn của dữ liệu.
  Từ đó, thời gian thực hiện của một thuật toán có 
 thể được đánh giá theo một hàm phụ thuộc vào 
 độ lớn đầu vào.
 Cấu trúc dữ liệu và giải thuật - HCMUS 2016
-HCMUS ©FIT 8
 49
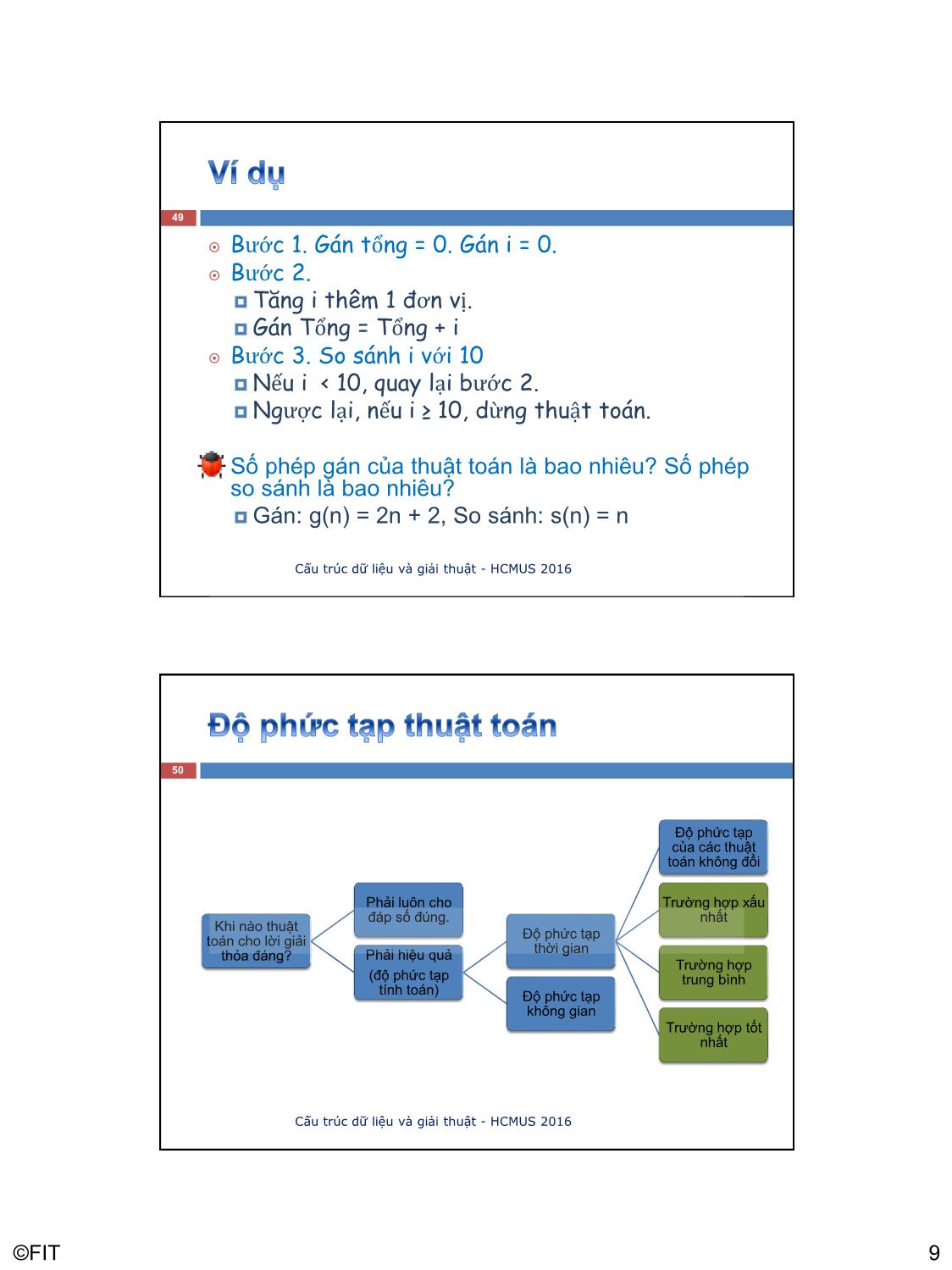
  Bước 1. Gán tổng = 0. Gán i = 0.
  Bước 2. 
  Tăng i thêm 1 đơn vị.
  Gán Tổng = Tổng + i
  Bước 3. So sánh i với 10
  Nếu i < 10, quay lại bước 2.
  Ngược lại, nếu i ≥ 10, dừng thuật toán.
  Số phép gán của thuật toán là bao nhiêu? Số phép
 so sánh là bao nhiêu?
  Gán: g(n) = 2n + 2, So sánh: s(n) = n
 Cấu trúc dữ liệu và giải thuật - HCMUS 2016
 50
 Độ phức tạp 
 của các thuật 
 toán không đổi
 Phải luôn cho Trường hợp xấu
 đáp số đúng. nhất
 Khi nào thuật 
 Độ phức tạp 
 toán cho lời giải 
 thời gian
 thỏa đáng? Phải hiệu quả
 Trường hợp
 (độ phức tạp trung bình
 tính toán) Độ phức tạp 
 không gian
 Trường hợp tốt 
 nhất
 Cấu trúc dữ liệu và giải thuật - HCMUS 2016
-HCMUS ©FIT 9
 51
  Thuật toán:
  B1. Đặt giá trị cực đại tạm thời 
 bằng số nguyên đầu tiên trong dãy.
  B2. So sánh số nguyên tiếp sau với 
 giá trị cực đại tạm thời. Nếu nó lớn 
 hơn giá trị cực đại tạm thời thì đặt 
 cực đại tạm thời bằng số nguyên đó.
  B3. Lặp lại B2 nếu còn các số nguyên 
 trong dãy.
  B4. Dừng khi không còn số nguyên nào 
 nữa trong dãy. Cực đại tạm thời 
 chính là số nguyên lớn nhất của dãy.
 Cấu trúc dữ liệu và giải thuật - HCMUS 2016
 52
  Vì phép sơ cấp sử dụng trong thuật toán là phép so 
 sánh, nên phép so sánh được dùng làm thước đo 
 độ phức tạp.
  Tại mỗi số hạng, ta thực hiện 2 phép so sánh, 1 
 phép xem đã hết dãy hay chưa và 1 phép so với 
 cực đại tạm thời.
  Vì hai phép so sánh được dùng từ số hạng thứ 2 
 đến n, và thêm 1 phép so sánh nữa để ra khỏi vòng 
 lặp, nên ta có chính xác 2(n-1) + 1 = 2n – 1 phép so 
 sánh.
  Do vậy, độ phức tạp của thuật toán là O(n).
 Cấu trúc dữ liệu và giải thuật - HCMUS 2016
-HCMUS ©FIT 10
 53
  Bước 1. Gán i = 1.
  Bước 2. Trong khi i ≤ n và x ai
 thì tăng i thêm 1.
 while (i ≤ n and x ai)
 i = i + 1
  Bước 3. 
  Nếu i ≤ n, trả về giá trị là i.
  Ngược lại, i > n, trả về giá trị 0 
 cho biết không tìm được x trong dãy 
 a.
 Cấu trúc dữ liệu và giải thuật - HCMUS 2016
 54
  Số phép so sánh dùng làm thước đo.
  Ở mỗi bước của vòng lặp, thực hiện 2 phép so 
 sánh.
  Cuối vòng lặp, thực hiện 1 phép so sánh.
  Như vậy, nếu x = ai, số phép so sánh thực hiện 
 là (2i +1).
  Trong trường hợp xấu nhất, không tìm được x 
 thì tổng số phép so sánh là 2n + 2. 
  Từ đó, thuật toán tìm kiếm tuần tự đòi hỏi tối đa 
 O(n) phép so sánh.
 Cấu trúc dữ liệu và giải thuật - HCMUS 2016
-HCMUS ©FIT 11
 55
  Trong trường hợp tốt nhất, ta bắt gặp x ngay 
 phần tử đầu tiên nên chỉ cần tốn 3 phép so 
 sánh.
  Khi đó, ta nói thuật toán tìm kiếm tuần tự đòi hỏi 
 ít nhất O(1) phép so sánh.
 Cấu trúc dữ liệu và giải thuật - HCMUS 2016
 56
  Nếu x là số hạng thứ i, số phép so sánh sử 
 dụng để tìm ra x là 2i + 1.
  Do đó, số phép so sánh trung bình ta cần sử 
 dụng là:
 n(n 1)
 2 n
 3 5 7 .. (2n 1) 2(1 2 3 ... n) n
 2 n 2
 n n n
  Như vậy độ phức tạp trung bình của thuật toán 
 tìm kiếm tuần tự là O(n)
 Cấu trúc dữ liệu và giải thuật - HCMUS 2016
-HCMUS ©FIT 12
 57
  Trong thực tế, các phép so sánh cần để xác định xem
 đã tới cuối vòng lặp hay chưa thường được bỏ qua,
 không đếm.
  Trong đa số các trường hợp không đòi khỏi sự khắt khe
 về tính chính xác, người ta sử dụng Big-O cho mọi
 trường hợp.
  Hệ số trong các hàm theo đa thức không được tính
 trong phân tích độ phức tạp, ví dụ O(n3) và O(20000n3)
 là như nhau, nhưng trong thực tế đôi khi hệ số rất quan
 trọng.
 Cấu trúc dữ liệu và giải thuật - HCMUS 2016
 58
 Độ phức tạp Thuật ngữ/tên phân lớp
 O(1) Độ phức tạp hằng số
 O(log2n) Độ phức tạp logarit
 O(n) Độ phức tạp tuyến tính
 O(nlog2n) Độ phức tạp nlog2n
 O(na) Độ phức tạp đa thức
 O(an), a > 1 Độ phức tạp hàm mũ
 O(n!) Độ phức tạp giai thừa
 Cấu trúc dữ liệu và giải thuật - HCMUS 2016
-HCMUS ©FIT 13
 59
 logn n nlogn n2 2n n!
 10 3.10-9 10-8 3.10-8 10-7 10-6 3.10-3
 102 7.10-9 10-7 7.10-7 10-5 4.1013 năm *
 103 1,0.10-8 10-6 1.10-5 10-3 * *
 104 1,3.10-8 10-5 1.10-4 10-1 * *
 105 1,7.10-8 10-4 2.10-3 10 * *
 106 2.10-8 10-3 2.10-2 17 phút * *
 • Lưu ý:
 • Mỗi phép toán giả sử thực hiện trong 10-9 giây (~ 
 CPU 1GHz).
 • *: thời gian lớn hơn 100100 năm
 Cấu trúc dữ liệu và giải thuật - HCMUS 2016
 60
  Có một số thuật toán có độ phức tạp trong trường 
 hợp xấu nhất là rất lớn nhưng trong trường hợp 
 trung bình lại chấp nhận được.
  Đôi khi, trong thực tế ta phải tìm nghiệm gần đúng 
 thay vì nghiệm chính xác.
  Có một số bài toán tồn tại nhưng có thể chứng 
 minh được không có lời giải cho chúng (ví dụ bài 
 toán Halting).
  Trong thực tế, đa số ta chỉ khảo sát các bài toán có 
 độ phức tạp đa thức trở xuống. 
 Cấu trúc dữ liệu và giải thuật - HCMUS 2016
-HCMUS ©FIT 14
 61
  Phương pháp đếm
  Phương pháp hàm sinh
  Một số kết quả hoán vị
  Các kết quả, định lý liên quan đến các cấu trúc 
 dữ liệu cụ thể
  
 Cấu trúc dữ liệu và giải thuật - HCMUS 2016
 62
 1. Các hàm sau đây có là O(x) hay không?
 a) f(x) = 10
 b) f(x) = 3x + 7
 c) f(x) = 2x2 + 2
 2. Mô tả thuật toán tìm số nhỏ nhất trong dãy hữu
 hạn các số tự nhiên. Có bao nhiêu phép so
 sánh, bao nhiêu phép gán trong thuật toán?
 Cấu trúc dữ liệu và giải thuật - HCMUS 2016
-HCMUS ©FIT 15
 63
 3. Phân tích độ phức tạp của thuật toán tính tổng dãy số sau:
 1 1 1
 S 1 ... 
 2 6 n!
 4. Cho biết số phép gán, số phép so sánh trong đoạn code sau 
 đây theo n:
 sum = 0;
 for (i = 0; i < n; i++)
 {
 scanf("%d", &x);
 sum = sum + x;
 }
 Cấu trúc dữ liệu và giải thuật - HCMUS 2016
 64
 5. Cho biết số phép gán, số phép so sánh trong đoạn 
 code sau đây theo n:
 for (i = 0; i < n ; i++)
 for (j = 0; j < n; j++)
 {
 C[i][j] = 0;
 for (k = 0; k < n; k++)
 C[i][j] = C[i][j] + 
 A[i][k]*B[k][j];
 }
 Cấu trúc dữ liệu và giải thuật - HCMUS 2016
-HCMUS ©FIT 16
 65
 6. Hãy cho biết các hàm số f(n) dưới đây là Big-O 
 của những hàm số g(n) nào?
  f(n) = (2 + n) * (3 + log2n)
  f(n) = 11 * log2n + n/2 – 3542
  f(n) = n * (3 + n) – 7 * n
 2
  f(n) = log2(n ) + n
 Cấu trúc dữ liệu và giải thuật - HCMUS 2016
 66
 Cấu trúc dữ liệu và giải thuật - HCMUS 2016
-HCMUS ©FIT 17