Bài giảng Cấu trúc dữ liệu và giải thuật - Bài: Cây cân bằng Red Black và AA
Red Black Tree (tt)
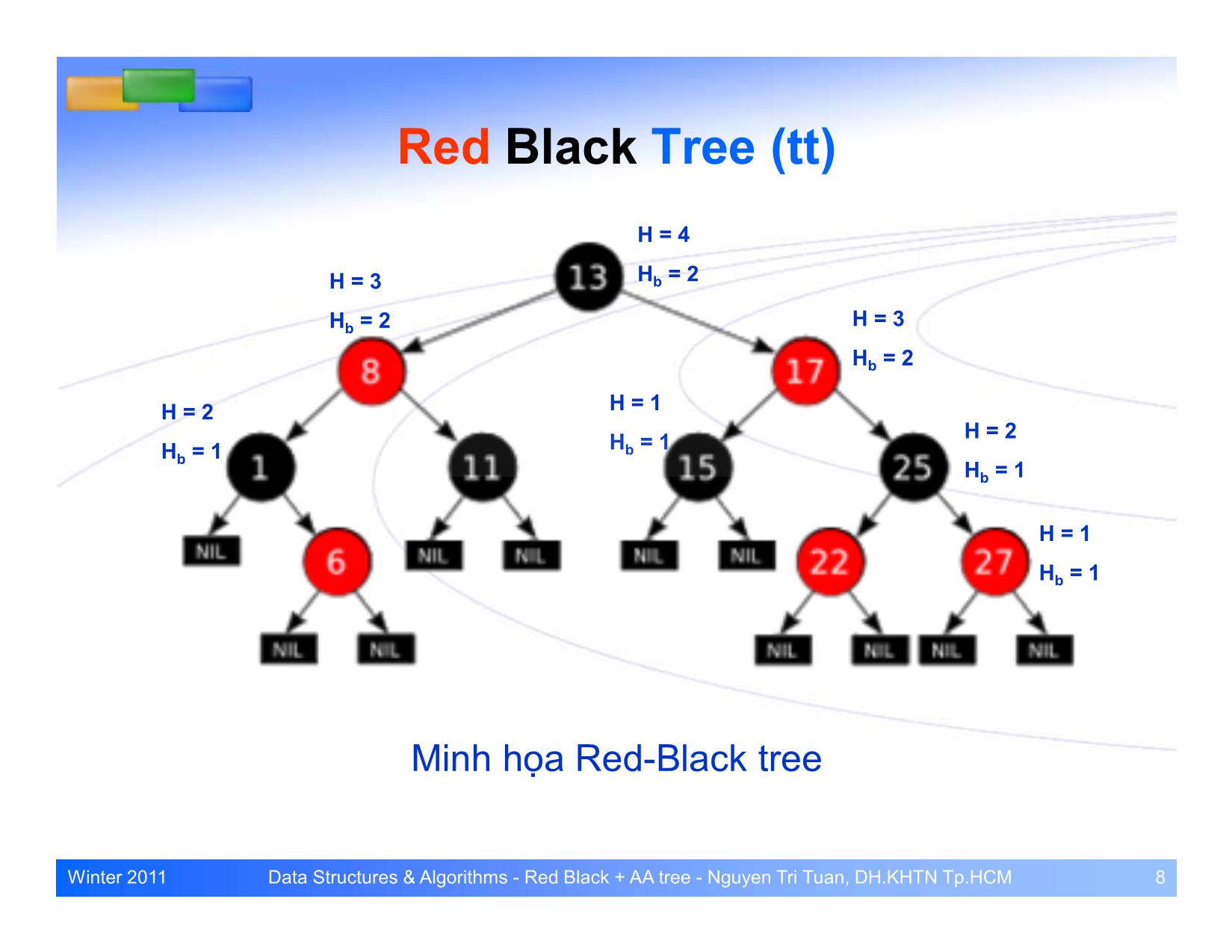
Định nghĩa: Red-Black tree là một cây nhị phân
tìm kiếm (BST) tuân thủ các quy tắc sau:
[1] Mọi node phải là đỏ hoặc đen
[2] Node gốc là đen
[3] Các node ngoài (external node; NULL node) mặc
định là những node đen
[4] Nếu một node là đỏ, những node con của nó phải
là đen
[5] Mọi đường dẫn từ gốc đến node ngoài phải có
cùng số lượng node đen
Trang 1

Trang 2

Trang 3
Trang 4
Trang 5
Trang 6

Trang 7

Trang 8
Trang 9
Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Cấu trúc dữ liệu và giải thuật - Bài: Cây cân bằng Red Black và AA", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Cấu trúc dữ liệu và giải thuật - Bài: Cây cân bằng Red Black và AA
Black Tree (tt)
RB_Insert_Node(T, z) // T: cây; z: node mới
y ← NULL; x ← root[T];
while x NULL { // đi đến nút lá
y ← x // y: node cha của x
if (key[z] < key[x]) x ← left[x];
else x ← right[x];
}
parent[z] ← y; // thêm node z vào cây
if (y == NULL) root[T] ← z; // là con của node y
else if (key[z] < key[y]) left[y] ← z;
else right[y] ← z;
left[z] ← NULL
right[z] ← NULL
color[z] ← RED // node mới z có màu đỏ
RB_Insert_FixUp(T, z) // điều chỉnh cây
Winter 2011 Data Structures & Algorithms - Red Black + AA tree - Nguyen Tri Tuan, DH.KHTN Tp.HCM 16
Red Black Tree (tt)
Cách thức điều chỉnh cây
Phép đảo màu
Phép xoay trái (Left-Rotation)
Phép xoay phải (Right-Rotation)
Winter 2011 Data Structures & Algorithms - Red Black + AA tree - Nguyen Tri Tuan, DH.KHTN Tp.HCM 17
Red Black Tree (tt)
Phép đảo màu
y
z
color[parent[z]] black
z
color[y] black
color[parent[parent[z]]] red
z = parent[parent[z]]
Winter 2011 Data Structures & Algorithms - Red Black + AA tree - Nguyen Tri Tuan, DH.KHTN Tp.HCM 18
Red Black Tree (tt)
Phép xoay trái (Left-Rotation):
Winter 2011 Data Structures & Algorithms - Red Black + AA tree - Nguyen Tri Tuan, DH.KHTN Tp.HCM 19
Red Black Tree (tt)
Ví dụ phép xoay trái
Winter 2011 Data Structures & Algorithms - Red Black + AA tree - Nguyen Tri Tuan, DH.KHTN Tp.HCM 20
Red Black Tree (tt)
RB_Left_Rotate(T, x)
y ← right[x];
right[x] ← left[y];
if (left[y] NULL) parent[left[y]] ← x;
parent[y] ← parent[x];
if (parent[x] == NULL) root[T] ← y;
else if (x == left[parent[x]])
left[parent[x]] ← y;
else right[parent[x]] ← y;
left[y] ← x;
parent[x] ← y;
Winter 2011 Data Structures & Algorithms - Red Black + AA tree - Nguyen Tri Tuan, DH.KHTN Tp.HCM 21
Red Black Tree (tt)
Phép xoay phải (Right-Rotation):
RB_Right_Rotate(T, x): tương tự hàm
xoay trái (tự viết)
Winter 2011 Data Structures & Algorithms - Red Black + AA tree - Nguyen Tri Tuan, DH.KHTN Tp.HCM 22
Red Black Tree (tt)
Tổng kết: có 6 trường hợp xử lý chi tiết
Trường hợp 1: áp dụng phép đảo màu
color[parent[z]] black
color[y] black
color[parent[parent[z]]] red
z = parent[parent[z]]
Winter 2011 Data Structures & Algorithms - Red Black + AA tree - Nguyen Tri Tuan, DH.KHTN Tp.HCM 23
Red Black Tree (tt)
Tổng kết: (tt)
Trường hợp 2: áp dụng phép đảo màu và xoay phải
color[parent[z]] black
color[parent[parent[z]]] red
RIGHT-ROTATE(T, parent[parent[z]])
Winter 2011 Data Structures & Algorithms - Red Black + AA tree - Nguyen Tri Tuan, DH.KHTN Tp.HCM 24
Red Black Tree (tt)
Tổng kết: (tt)
Trường hợp 3: áp dụng xoay trái để đưa về dạng 2
Case 3 Case 2
z parent[z]
LEFT-ROTATE(T, z)
“Xử lý như trường hợp 2”
Winter 2011 Data Structures & Algorithms - Red Black + AA tree - Nguyen Tri Tuan, DH.KHTN Tp.HCM 25
Red Black Tree (tt)
Thêm 4
11 Case 1 11 Case 3
2 14 2 14 y
z
1 7 15 1 7 15
5 8 y 5 8
z 4 4
11
Case 2 7
7 14 y z
z 2 11
2 8 15
1 5 8 14
1 5
4 15
4
Winter 2011 Data Structures & Algorithms - Red Black + AA tree - Nguyen Tri Tuan, DH.KHTN Tp.HCM 26
Red Black Tree (tt)
Tổng kết: (tt)
3 trường hợp tương tự [1’], [2’], [3’] đối xứng với [1],
[2], [3] qua trục Y
Case [2’]
Case [1’]
Case [3’]
Winter 2011 Data Structures & Algorithms - Red Black + AA tree - Nguyen Tri Tuan, DH.KHTN Tp.HCM 27
Red Black Tree (tt)
RB_Insert_FixUp(T, z)
while (color[parent[z]] == RED) {
// trường hợp [1], [2], [3]
if (parent[z] == left[parent[parent[z]]]) {
y ← right[parent[parent[z]]];
if (color[y] == RED) “Case 1”;
else {
if (z == right[parent[z]]) “Case 3”;
“Case 2”;
}
}
else // trường hợp [1’], [2’], [3’]
color[root[T]] ← BLACK
Winter 2011 Data Structures & Algorithms - Red Black + AA tree - Nguyen Tri Tuan, DH.KHTN Tp.HCM 28
Red Black Tree (tt)
Đánh giá thao tác Insert node:
Chi phí thêm phần tử mới (z): O(log2N)
Chi phí của RB_Insert_FixUp: O(log2N)
Chi phí tổng cộng: O(log2N)
Winter 2011 Data Structures & Algorithms - Red Black + AA tree - Nguyen Tri Tuan, DH.KHTN Tp.HCM 29
Red Black Tree (tt)
Delete node:
Cách thức xóa 1 node: giống như BST
Demo chương trình
Nếu node bị xoá có màu đỏ: không gây ra vi phạm
Mọi node phải là đỏ hoặc đen OK
Node gốc là đen OK
Các node lá (NULL) phải luôn luôn đen OK
Nếu một node là đỏ, những node con của nó phải là đen
OK vì không tạo ra 2 node liên tiếp màu đỏ
Mọi đường dẫn từ gốc đến nút lá phải có cùng số lượng
node đen OK vì không làm thay đổi số node đen
Winter 2011 Data Structures & Algorithms - Red Black + AA tree - Nguyen Tri Tuan, DH.KHTN Tp.HCM 30
Red Black Tree (tt)
Delete node: (tt)
Nếu node bị xoá có màu đen: có thể gây ra vi phạm
Mọi node phải là đỏ hoặc đen OK
Node gốc là đen not OK ! Vì có thể xóa root và thay bằng node
đỏ
Các node lá (NULL) phải luôn luôn đen OK
Nếu một node là đỏ, những node con của nó phải là đen not OK
! Vì có thể tạo ra 2 node liên tiếp màu đỏ
Mọi đường dẫn từ gốc đến nút lá phải có cùng số lượng node đen
not OK ! Vì làm giảm đổi số node đen
Xem chi tiết “Data structure & Analysis in C”, p. 465
Winter 2011 Data Structures & Algorithms - Red Black + AA tree - Nguyen Tri Tuan, DH.KHTN Tp.HCM 31
Red Black Tree (tt)
Đánh giá:
Ưu điểm:
Chi phí tìm kiếm O(log2N)
Insert O(log2N)
Delete O(log2N)
Minimum O(log2N)
Maximum O(log2N)
Hạn chế:
Phải lưu trữ thuộc tính màu (color) và con trỏ đến nút cha
(pParent)
Cài đặt phức tạp hơn cây AVL và AA
Winter 2011 Data Structures & Algorithms - Red Black + AA tree - Nguyen Tri Tuan, DH.KHTN Tp.HCM 32
Cây cân bằng Red Black và AA
Review
Giới thiệu
Cây Đỏ – Đen (Red Black Tree)
AA – Tree
Winter 2011 Data Structures & Algorithms - Red Black + AA tree - Nguyen Tri Tuan, DH.KHTN Tp.HCM 33
AA (Arne Andersson) – Tree
Minh họa
Các khái niệm
Định nghĩa
Cấu trúc lưu trữ
Các thao tác cơ bản
Đánh giá
Winter 2011 Data Structures & Algorithms - Red Black + AA tree - Nguyen Tri Tuan, DH.KHTN Tp.HCM 34
AA – Tree (tt)
Liên kết
ngang
Liên kết Liên kết
con trái 30 70 con phải
15 50 60 85
80 90
5 10 20 35 40 55 65
Minh họa cấu trúc cây AA
Winter 2011 Data Structures & Algorithms - Red Black + AA tree - Nguyen Tri Tuan, DH.KHTN Tp.HCM 35
AA – Tree (tt)
Các khái niệm:
Mức (Level) của một node
Liên kết ngang (Horizontal link)
Xoay phải (Right rotation – Skew)
Xoay trái (Left rotation – Split)
Winter 2011 Data Structures & Algorithms - Red Black + AA tree - Nguyen Tri Tuan, DH.KHTN Tp.HCM 36
AA – Tree (tt)
Các khái niệm: (tt)
Mức (Level) của một node: là số liên kết trái từ node
đó đến NULL
Mức của node NULL là 0
Mức của node lá là 1
Mức 2 A B
Mức 1 C D E
Winter 2011 Data Structures & Algorithms - Red Black + AA tree - Nguyen Tri Tuan, DH.KHTN Tp.HCM 37
AA – Tree (tt)
Các khái niệm: (tt)
Liên kết ngang (Horizontal link): là liên kết giữa một
node và node con của node đó ở cùng một mức
Node con
Node cha ở cùng mức
A B
C D E
Winter 2011 Data Structures & Algorithms - Red Black + AA tree - Nguyen Tri Tuan, DH.KHTN Tp.HCM 38
AA – Tree (tt)
Các khái niệm: (tt)
Xoay phải (Skew): xóa bỏ liên kết ngang bên trái
Sử dụng để điều chỉnh cây
t
t1 t
X P X P
A B C A B C
Winter 2011 Data Structures & Algorithms - Red Black + AA tree - Nguyen Tri Tuan, DH.KHTN Tp.HCM 39
AA – Tree (tt)
Các khái niệm: (tt)
Xoay trái (Split): xoá bỏ 2 liên kết ngang liên tiếp bên
phải
t
Sử dụng để điều chỉnh cây
t t1 R
X R G
X G
A B
A B
Winter 2011 Data Structures & Algorithms - Red Black + AA tree - Nguyen Tri Tuan, DH.KHTN Tp.HCM 40
AA – Tree (tt)
Skew có thể tạo ra nhiều liên kết ngang phải liên
tiếp sử dụng Split để điều chỉnh
3 5 10
Skew 5
Split
3 5 10
3 10
Winter 2011 Data Structures & Algorithms - Red Black + AA tree - Nguyen Tri Tuan, DH.KHTN Tp.HCM 41
AA – Tree (tt)
Định nghĩa: AA tree là một cây nhị phân tìm
kiếm (BST) tuân thủ các quy tắc sau:
Liên kết ngang luôn hướng về bên phải
Không có 2 liên kết ngang liên tiếp nhau
Mọi node có mức > 1 sẽ có 2 node con
Nếu một node không có liên kết ngang phải thì 2
node con của nó ở cùng mức
Winter 2011 Data Structures & Algorithms - Red Black + AA tree - Nguyen Tri Tuan, DH.KHTN Tp.HCM 42
AA – Tree (tt)
Liên kết ngang
luôn hướng về Không có 2
Node có
bên phải liên kết ngang
mức > 1
liên tiếp
có 2 con 30 70
15 50 60 85
80 90
5 10 20 35 40 55 65
2 node con cùng mức
khi node cha không có
liên kết ngang
Winter 2011 Data Structures & Algorithms - Red Black + AA tree - Nguyen Tri Tuan, DH.KHTN Tp.HCM 43
AA – Tree (tt)
Tính chất:
Level của node con trái luôn nhỏ hơn level của node
cha 1 đơn vị
Level của node con phải nhỏ hơn hay bằng level của
node cha (nhưng không quá 1 đơn vị)
Thêm một node luôn thực hiện ở node có mức = 1
Winter 2011 Data Structures & Algorithms - Red Black + AA tree - Nguyen Tri Tuan, DH.KHTN Tp.HCM 44
AA – Tree (tt)
Cấu trúc lưu trữ:
typedef int DataType; // Kiểu dữ liệu
typedef struct NodeTag {
DataType key; // Dữ liệu
struct NodeTag *pLeft;
struct NodeTag *pRight;
int level; // mức của node
} AANode;
typedef struct AANode* AATREE;
Winter 2011 Data Structures & Algorithms - Red Black + AA tree - Nguyen Tri Tuan, DH.KHTN Tp.HCM 45
AA – Tree (tt)
Các thao tác cơ bản:
Khi thêm 1 node
Node thêm vào bên trái tạo ra một liên kết ngang bên trái
thực hiện Skew
Node thêm vào bên phải nếu tạo ra 2 liên kết ngang liên
tiếp bên phải thực hiện Split
30 70
15 50 60 85
3 5 10 20 35 40 48 55 65 80 90
Skew Split
Winter 2011 Data Structures & Algorithms - Red Black + AA tree - Nguyen Tri Tuan, DH.KHTN Tp.HCM 46
AA – Tree (tt)
Các thao tác cơ bản: (tt)
Tìm một phần tử: hoàn toàn giống cây BST
30 70
15 50 60 85
80 90
5 10 20 35 40 55 65
Tìm “55”
Winter 2011 Data Structures & Algorithms - Red Black + AA tree - Nguyen Tri Tuan, DH.KHTN Tp.HCM 47
AA – Tree (tt)
Các thao tác cơ bản: (tt)
Thêm một node:
30 70
15 50 60 85
5 10 20 35 40 45 55 65 80 90
Cần Split Thêm “45”
Winter 2011 Data Structures & Algorithms - Red Black + AA tree - Nguyen Tri Tuan, DH.KHTN Tp.HCM 48
AA – Tree (tt)
Các thao tác cơ bản: (tt)
Thêm một node:
30 70
15 40 50 60 85
5 10 20 35 45 55 65 80 90
Cần Skew
Sau khi Split tại “35”
Winter 2011 Data Structures & Algorithms - Red Black + AA tree - Nguyen Tri Tuan, DH.KHTN Tp.HCM 49
AA – Tree (tt)
Các thao tác cơ bản: (tt)
Thêm một node:
Cần Split
30 70
15 40 50 60 85
5 10 20 35 45 55 65 80 90
Sau khi Skew tại “50”
Winter 2011 Data Structures & Algorithms - Red Black + AA tree - Nguyen Tri Tuan, DH.KHTN Tp.HCM 50
AA – Tree (tt)
Các thao tác cơ bản: (tt)
Thêm một node: Cần Skew
Cần Split
30 70
50
15 40 60 85
5 10 20 35 45 55 65 80 90
Sau khi Split tại “40”
Winter 2011 Data Structures & Algorithms - Red Black + AA tree - Nguyen Tri Tuan, DH.KHTN Tp.HCM 51
AA – Tree (tt)
Các thao tác cơ bản: (tt)
Thêm một node:
50
30 70
15 40 60 85
5 10 20 35 45 55 65 80 90
Sau khi Skew tại “70”, và Split tại “30”
STOP !
Winter 2011 Data Structures & Algorithms - Red Black + AA tree - Nguyen Tri Tuan, DH.KHTN Tp.HCM 52
AA – Tree (tt)
Demo chương trình
Winter 2011 Data Structures & Algorithms - Red Black + AA tree - Nguyen Tri Tuan, DH.KHTN Tp.HCM 53
AA – Tree (tt)
AATREE AA_Insert_Node(DataType x, AATREE t)
{
if(t == NULL) { // tạo node mới và thêm vào cây
t = new AANode;
t->key = x;
t->pLeft = t->pRight = NULL;
t->level = 1;
}
else if(x key)
t->pLeft = AA_Insert_Node(x, t->pLeft);
else if(x > t->key)
t->pRight = AA_Insert_Node(x, t->pRight);
else return t; // trùng khóa
t = Skew(t);
t = Split(t);
return t;
}
Winter 2011 Data Structures & Algorithms - Red Black + AA tree - Nguyen Tri Tuan, DH.KHTN Tp.HCM 54
AA – Tree (tt)
AATREE right_rotate(AATREE &t)
{
AATREE t1;
t1 = t->pLeft;
t->pLeft = t1->pRight;
t1->pRight = t;
return t1;
}
AATREE Skew(AATREE &t)
{
if (t->pLeft != NULL)
if (t->pLeft->level == t->level)
t = right_rotate(t);
return t;
}
Winter 2011 Data Structures & Algorithms - Red Black + AA tree - Nguyen Tri Tuan, DH.KHTN Tp.HCM 55
AA – Tree (tt)
AATREE left_rotate(AATREE &t)
{
AATREE t1;
t1 = t->pRight;
t->pRight = t1->pLeft;
t1->pLeft = t;
t1->level++;
return t1;
}
AATREE Split(AATREE &t)
{
if (t->pRight !=NULL)
if (t->pRight->pRight != NULL)
if (t->pRight->pRight->level == t->level)
t = left_rotate(t);
return t;
}
Winter 2011 Data Structures & Algorithms - Red Black + AA tree - Nguyen Tri Tuan, DH.KHTN Tp.HCM 56
AA – Tree (tt)
Các thao tác cơ bản: (tt)
Thêm một node: VD. thêm “6”
4 10
2 8 12
1 3 5 7 9 11 13
6 ??
Winter 2011 Data Structures & Algorithms - Red Black + AA tree - Nguyen Tri Tuan, DH.KHTN Tp.HCM 57
AA – Tree (tt)
Các thao tác cơ bản: (tt)
Xóa một node:
Giảm mức 4 10
2 6 8 12
1 3 5 7 9 11 13
Xóa “1”
Winter 2011 Data Structures & Algorithms - Red Black + AA tree - Nguyen Tri Tuan, DH.KHTN Tp.HCM 58
AA – Tree (tt)
Các thao tác cơ bản: (tt)
Xóa một node: Giảm mức
4 10
6 8 12
2 3 5 7 9 11 13
Sau khi giảm mức tại “2”
Winter 2011 Data Structures & Algorithms - Red Black + AA tree - Nguyen Tri Tuan, DH.KHTN Tp.HCM 59
AA – Tree (tt)
Các thao tác cơ bản: (tt)
Xóa một node:
Cần Skew
4 10
6 8 12
2 3 5 7 9 11 13
Sau khi giảm mức tại “4” và “10”
Winter 2011 Data Structures & Algorithms - Red Black + AA tree - Nguyen Tri Tuan, DH.KHTN Tp.HCM 60
AA – Tree (tt)
Các thao tác cơ bản: (tt)
Xóa một node: Cần Skew
4 6 10
8 12
2 3 5 7 9 11 13
Sau khi Skew tại “10”, lần 1
Winter 2011 Data Structures & Algorithms - Red Black + AA tree - Nguyen Tri Tuan, DH.KHTN Tp.HCM 61
AA – Tree (tt)
Các thao tác cơ bản: (tt)
Xóa một node: Cần Split
4 6 8 10 12
2 3 5 7 9 11 13
Sau khi Skew tại “10”, lần 2
Winter 2011 Data Structures & Algorithms - Red Black + AA tree - Nguyen Tri Tuan, DH.KHTN Tp.HCM 62
AA – Tree (tt)
Các thao tác cơ bản: (tt)
Xóa một node:
6 Cần Split
4 8 10 12
2 3 5 7 9 11 13
Sau khi Split tại “4”
Winter 2011 Data Structures & Algorithms - Red Black + AA tree - Nguyen Tri Tuan, DH.KHTN Tp.HCM 63
AA – Tree (tt)
Các thao tác cơ bản: (tt)
Xóa một node:
6 10
4 8 12
2 3 5 7 9 11 13
Sau khi Split tại “8” STOP !
Winter 2011 Data Structures & Algorithms - Red Black + AA tree - Nguyen Tri Tuan, DH.KHTN Tp.HCM 64
AA – Tree (tt)
Đánh giá:
Độ phức tạp O(log2N)
Không cần lưu con trỏ đến node cha (pParent)
Cài đặt đơn giản hơn cây Red-Black
Winter 2011 Data Structures & Algorithms - Red Black + AA tree - Nguyen Tri Tuan, DH.KHTN Tp.HCM 65File đính kèm:
 bai_giang_cau_truc_du_lieu_va_giai_thuat_bai_cay_can_bang_re.pdf
bai_giang_cau_truc_du_lieu_va_giai_thuat_bai_cay_can_bang_re.pdf

