Architecture and stability of the second–order cellular neural networks

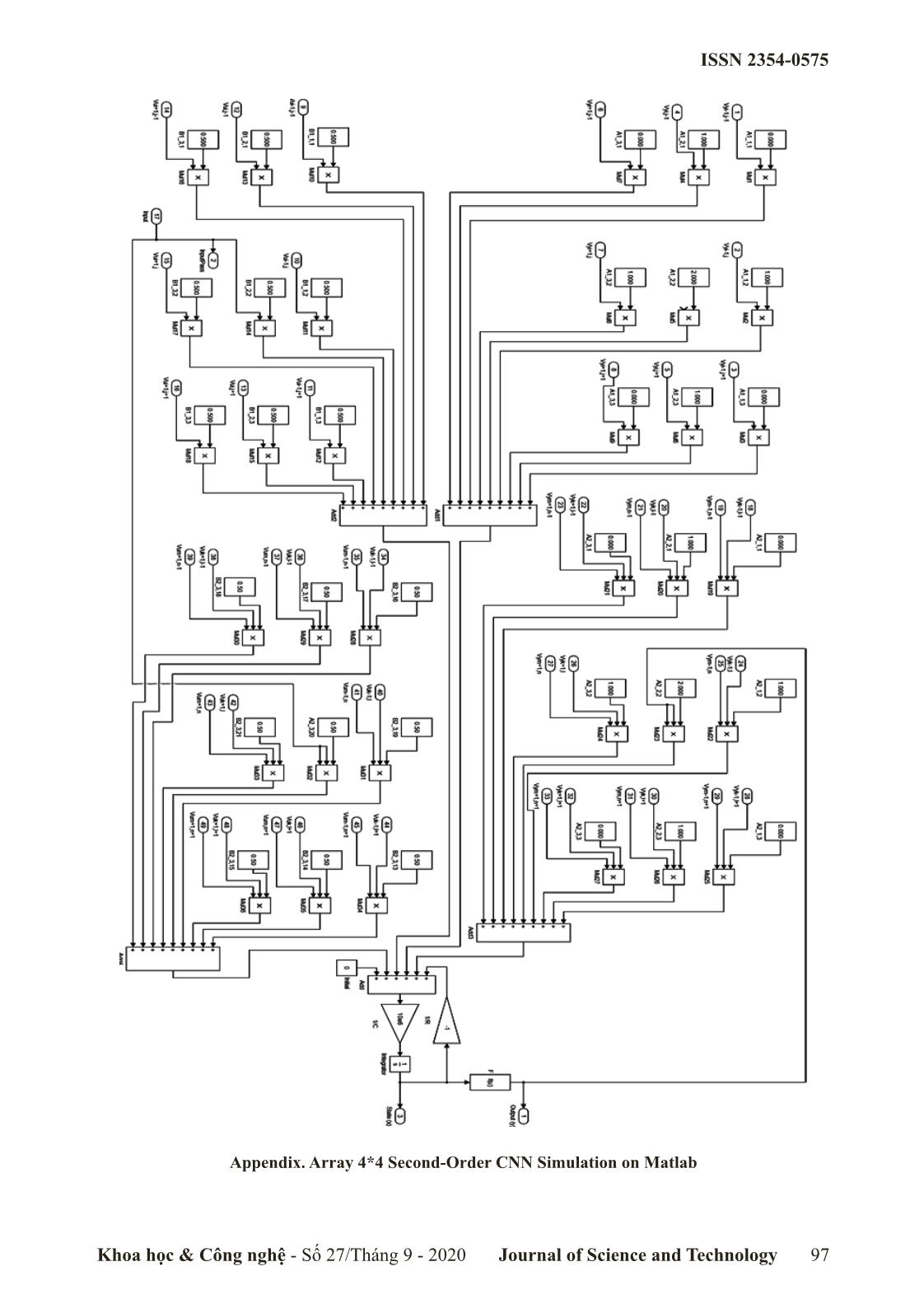
with the 2nd-order polynomial inputs and extended 
Khoa học & Công nghệ - Số 27/Tháng 9 - 2020 Journal of Science and Technology 91
ISSN 2354-0575
 Parameter assumptions: (symmetry properties)
 A(i,j; k,l) = A(k,l;i,j);
 A(i,j; k,l; m,n)=A(i,j; m,n; k,l)=A(k,l; i,j; m,n)=
 = A(k,l; m,n; i,j)=A(m,n; i,j; k,l)=A(m,n; k,l; i,j) 
 1 ≤ i ≤ M; 1 ≤ j ≤ N (2.6)
 Remarks: 
 a) All inner cells of SOCNN that have the same 
 Figure 1. The neighborhood of cell C(i, j) element values and structure. The inner cell C(i,j) 
 ,; ,
 defined by(2.1) a) r=1, b) r=2 respectively is the cell in the operand: /Ck,l Aijkl .ykl(t) has 
 ^ h ^ h
 21r + 2 neighborhood connections, where r is 
 ^h
 SOCNN architecture can be defined as follows: defined in (2.1). 
 ,; ,
State equation (see architecture in Figure 3): In the operand: /Ck,l Bijkl .ukl we also 
 ^ h ^ h
 21+ 2
 dxij () t 1 have r neighborhood connections. So: 
 C =−+x() t∑ Ai (, j ; k , l ) y () t + ^h
 ij kl ∑∑A(i, j;k,l;m,n)y() t y () t
 dt C( kl ,) kl mn
 R ckl( ,) cmn ( , )
 ++∑ ∑∑ 2
 Bi(, jklu ; , ) kl Bi(, jklmnu ; , , , ) kl u mn in these two operands have 22r + 1 neighborhood 
 Ckl( ,) CklCmn( ,) ( , ) ^h
 connections. 
 ++∑∑Ai(, j ; k ,, l mn , ) ykl () t y mn () t I
 CklCmn( ,) ( , ) The operand ∑∑A(i, j;k,l;m,n)y() t y () t
 kl mn
 ckl( ,) cmn ( , )
 (2.2) and the operand
with A(), B() is feedback coefficient, input ∑∑B(i, j;k,l;m,n)u u
 kl mn
coefficient matrix respectively; R is linear resistor ckl( ,) cmn ( , )
 2
usually chosen to be between 1KX and 1MX; C have 21r + 2 neighborhood cells for each 
 6@^h
is linear capacitor usually chosen to be 1n F; I is respectively. Usually, we call these two operands 
cellular bias or cellular threshold of the CNN cell. proposed by us are second–order operands in the 
Output equation: (see Figure 2): sense that they attach with the production of two 
  11xt( ) ≥ feedback output signals ytkl .ytmn and the 
  ij ^^hh
 ytij ( ) = x −≤11 xtij ( ) ≤ (2.3) production of two input signals uukl . mn. Finally we 
 2 2
 − ≤− have 2 21r + neighborhood connections to the 
  11xtij ( ) 6@^h
 cell C(i, j).
Input equation: u = E = constant
 ij ij b) The dynamics of SOCNN has two parts: one part 
 1 ≤ i ≤ M; 1 ≤ j ≤ N (2.4)
 includes the input operands: ∑ A(i, j;k,l)y ()t
 kl
Constraint equations: ckl( ,)
 with the feedback yt() and ∑ B(i, j;k,l)u
 |xij(0)| ≤ 1; |uij| ≤ 1 (2.5) kl, kl
 c( mn ,)
We can always be normalized to satisfy these 
 with input variable ukl . Other part (added by us):
conditions.
 ∑∑A(i, j;k,l;m,n)y() t y () t
 kl mn
 ckl( ,) cmn ( , )
 with production of two the feedback variables
 ykl() ty mn () t and ∑∑B(i, j;k,l,m,n)ukl u mn
 C( kl , )( mn , )
 with production of two the input variables uukl mn .
 3. Stability of Second-Order CNN
 Since Our SOCNN have feedback output 
 signals, may be not stable to the system. One of 
 the most effective technique analizing the stability 
 properties of dynamic nonlinear system is Lyapunov 
 method. Hence, let us first define a Lyapunov 
 Figure 2. Output Characteristics of CNN function for the SOCNN. 
92 Khoa học & Công nghệ - Số 27/Tháng 9 - 2020 Journal of Science and Technology
 ISSN 2354-0575
Definition 2: We define the Lyapunov function E(t) Depending on (3.3) and (3.5) equation that E(t) is 
of the SOCNN by scalar function: bounded, but we can also prove that it is a monotone 
 112 decreasing function.
 E(t)= -∑∑ A(i, j;k,l)yij (t)ykl (t)+∑ yij (t)
 2 (i, j)(k,l) 2R (i, j)
 Theorem 2: The scalar function E(t) defined in 
 -∑∑ B(i, j;k,l)yij (t)ukl
 (i, j)(k,l) (3.2) is a monotone decreasing function (or minus–
  1 defined function), that is
 + -∑∑ ∑ A(i, j;k,l;m,n)y (t)y (t)y (t)-
  ij kl mn dE() t (3.6)
  3 (i, j)(k,l)(m,n) ≤ 0
  dt
 -∑∑ ∑ B(i, j;k,l;m,n)yij (t)ukl u mn  -∑ Iyij (t); This is the 2nd condition for E(t) to become 
 (i, j)(k,l)(m,n)  (i, j)
 Lyapunov function. 
 (3.1)
 Operands in the square braskets are proposed Proof: To differentiate E(t) in (3.2) with to time t, 
by us. In the following theorem, we will prove take the derivate of on the right side of (3.2) with 
 st
E(t) is bounded. This is the 1 condition for E(t) to respect to xij(t):
become Lyapunov function.
 dE(t) dyij (t) dx ij (t)
Theorem 1: Function E(t) defined in (3.1) is bounded =∑∑ A(i, j;k,l) +
 (i, j) (k,l)
by: max E() t≤ Emax (3.2) dt dxij (t) dt
 1 dy (t)
 ++1 ij dxij (t) dyij (t) dx ij (t)
 Emax =∑∑ A(i, j;k,l)∑∑ B(i, j;k,l) ∑∑−
 (i, j) (k,l) (i, j) (k,l) + y(t)ij - I 
 2 (i, j) (i, j)
 Rx dxij (t) dt dxij dt
 11
 ++MN() I + ∑∑ ∑ A(i, j;k,l;m,n) +
 dyij (t) dx ij (t)
 (i, j) (k,l) (m,n)
 2R 3 -∑∑ B(i, j;k,l) ukl −
 (i, j) (k,l)
 dxij (t) dt
 + ∑∑ ∑ B(i, j;k,l;m,n) (3.3)
 (i, j) (k,l) (m,n)
 dyij(t) dx ij (t)
 − ∑∑∑ A(i, j;k,l;m,n) ykl y mn (t)
Proof: Following to the definition of E(t) in (3.1), (i, j) (k,l) (mn)
 dxij (t) dt
we have:
 dy (t) dx (t)
 Et()≤ 0 (3.4) ij ij
 -∑∑∑ B(i, j;k,l;m,n) ukl u mn
 (i, j) (k,l) (mn)
Since ytij , uij are bounded as claimed in (2.5) dxij (t) dt
 ^h
we have: (3.7)
 1
 Et()≤ Emax =∑∑ A(i, j;k,l)++∑∑ B(i, j;k,l) Here, we use the symmetry properties of (2.6) 
 2 (i, j) (k,l) (i, j) (k,l)
 to obtain (3.7). From the output function (2.3), we 
 1 1
 +MN ++I ∑∑ ∑ A(i, j;k,l;m,n) obtain the following relations:
 2R (i, j) (k,l)( m, n)
 3 1 (3.8)
 dyij t = if |x (t)| < 1
 + ^ h ij
 ∑∑ ∑ B(i, j;k,l;m,n) dxij t (0 if |x (t)| $ 1
 (i, j) (k,l) (m,n) ^ h ij
 and when |x (t)| < 1, y (t) = x (t)
 1 ≤ i, k, m ≤ M ; 1 ≤ j, l, n ≤ N (3.5) ij ij ij
 Figure 3. Model of Second-Order CNN
Khoa học & Công nghệ - Số 27/Tháng 9 - 2020 Journal of Science and Technology 93
ISSN 2354-0575
According to our definitions ofSOCNN , have: 1
 fij () t = ∑ Ai(, jkl ; ,) ykl () t
 A(i, j; k, l) = A(i, j; k, l; m, n) = B(i, j; k, l)= C C( k ,) l∈ Nr (, i j )
 = B(i, j; k, l; m, n) = 0 1
 =
for C (k, l) g N (i, j); C (m, n) g N (i, j) gij () t ∑ Bi(, jklu ; , ) kl
 r r C C( k ,) l∈ Nr (, i j )
It follows from (3.7) and (3.8) with the parameter 1
assumptions: hij () t = ∑ Ai(, jklmn ; ,; , ) ykl () t y mn () t
 C Ckl( , ), Cmn ( , )∈ Nrij ( , )
 dE() t dyij() t dx ij () t  1 1
 ∑ −+ 1
 =-  xtij() xt ij () = ∑
 dt(i, j) dxij () t dt R R pij () u Bi(, jklmnu ; ,; , ) kl u mn
 C Ckl( , ), Cmn ( , )∈ Nrij ( , )
 + ∑∑B(i, j;k,l)ukl + A(i, j;k,l)ykl () t
 C(k,l)∈∈ N (i, j) C(k,l) N (i, j)
 rrwith uE= ij indicates an M*N
 6@1xMN
 + ∑∑A(i, j;k,l;m,n)ykl() t y mn () t
 ∈∈ dimentional constant input vector. Formula (3.11) 
 C(k,l) Nrr (i, j) C(m,n) N (i, j)
 is a 1st–order ordinary diffential equation and its 
 
 + ∑∑B(i, j;k,l;m,n)ukl u mn  solution is given by:
 ∈ ∈
 C(k,l) Nr (i, j) C(m,n) Nr (i, j)  t
 1 --t x
 - RC _iRC
 2 xtij = xij 0 e + # e ftij + gtij +
= dxij () t __ii 8 _i _i
 −≤∑ C0 (3.9) (3.9) 0
 ij dt + ptij + qtij + Idl x (3.12)
 _i _i B
Remark: It follow that: 
 Colollary: For any given inputs uij and any −t
 RC
 xtij( )= x ij (0) e +
initial states xij(t) of the SOCNN, we have:
 lim = (3.10) t −−()t τ
 Et constant RC '
 t " 3 ^h +e f()ττ ++ h () gu () + pu () + I dτ
 ∫ ij ij ij ij
and: 0
 dE t
 lim ^h= 0 (3.10a) −t
 t " 3 dt xt( )≤+ x (0) eRC
Proof: ij ij
 From theorems 1 and 2, E(t) is bounded −−τ
 t ()t '
 +eRC  f()ττ++ h () gu () + pu () + I dτ
monotone decreasing of time t. Therefore, E(t) ∫ ij ij ij ij
 0 
converges to a limit and its derivate converges to 
 −t
zero (0). RC
 ≤+xeij (0)
Theorem 3:
 t −−()t τ
 RC '
 All states xij(t) in SOCNN are limitted for all + e f()ττ+++ gu () h () pu () + I d τ ≤
 ∫ ij ij ij ij
 0 
time t >0 and the xmax can be computed by:
 −t t −−()t τ
  ≤x(0) eRC + FGH + + ++ P I' eRC dτ
 ∑ + ij ij ij ij ij ∫
 xmax = R max  ( A(i, j;k,l) + B(i, j;k,l)) 1 0
 (1≤≤ i M; j ≤≤1 N ) ∈
 C(k,l) Nr (i, j)
 ≤x(0) + RC F + G + H ++ P I'
  ij ij ij ij ij
 ++RI ∑∑( Ai(, jklmn ; ,; , )+ Bi (, jklmn ; ,; , )) ;
 C( k ,) l∈∈ Nr (, i j ) C ( m , n ) Nr (, i j )  (3.13)
 (3.10) where: 
 Ffij = max ij t
Proof: t _i
 1 ,; , max
From formula (2.1), we can rewrite the kinetic # / Aijkl ytkl (3.14)
 C Ck,,lN! rij _it _i
equation of the cell as follow: __ii
 = # 1 ,; , max
 dxij () t 1 Gmij ax gtij / Bijkl ukl
 u _i C Ck,l _iu
 =−++xtij() ft ij () gu ij ( ) + _i
 dt RC (3.14b)
 (3.11)
 ++ht() pu ( ) + I '
 ij ij Hmij = ax htij #
 t _i
 1 ,; ,; , max max
where: # / Aijklmn ytkl ytmn 
 I C Ck,,lCmn, ^ht ^h t ^h
 Il = __ii
 C (3.14c)
94 Khoa học & Công nghệ - Số 27/Tháng 9 - 2020 Journal of Science and Technology
 ISSN 2354-0575
 SR WV
 Pmij = ax puij # R V S0 0 0 0W
 u _i S05. 05. 05. W S W
 S W S0 0 0 0W
 B= S05. 05. 05. W ; I= S W
 1 ,; ,; , max max S W S0 0 0 0W
# / Bijklmn ukl umn S05. 05. 05. W S W
 C Ck,,lCmn, ^hu u S W S W
 __ii T X S0 0 0 0W
 (3.14d) T X
 Parameters for standard CNN and SOCNN 
Since xij(0) and uij satisfy the conditions in (2.5), 
 4*4 cells (N=4, M=4); C=10-9 F; R=103 X ; cellular 
while |yij(t)| satisfies the conditions: 
 bias I; Initial state values:
 ytij () # 1, 6t
In view of characteristics function (2.3), it follows 
from (3.13) and (3.14): x(t=0) = 
|xij(t)|
# ,; , l All the data are being used to simulate on 
 |xij(0)| + R / Aijkl max|ykl(t)| + I
 9Cm(,n) ^h Matlab (2014) for standard CNN and SOCNN with 
 ,; , max 4*4=16 state variables X for purpose to compare. 
+ / Bijkl ukl +
 Cm,n ^ h
 ^ h Figure 4a and 4b are the transient behaviors of 
 ,; ,, , max max
+ / / Aijklmn ytkl ytmn the standard CNN and SOCNN respectively, that 
 Ck,l Cm,n ^ht ^h t ^h
 ^hh ^ take two cells X , X for the examples (in total 
 ,; ,; , max max 11 22
+ / / Bijklmn ukl + umn
 Ckl Cmn ^hu u C 16 transient behaviors). From Fig.4a and 4b we 
 ^hh ^ (3.15)
 can remark that: i) CNN and SOCNN reach to the 
 equilibrium stability state after some time. ii) The 
 ,; ,, ,
xmax = 1 + R|I| + / / Aijklmn + 
 Ck,l Cm,n ^h transient behaviors of SOCNN monoton-increasing 
 ^hh ^
 + / / Bi,;jk,;lm,n (3.16) to the equilibrium state, no has overshoot. In 
 Ck,l Cm,n ^h
 ^hh ^ standard CNN presented by Leon O. Chua [2] the 
Because xmax depend on the time t and the cell C(i,j), transient behaviors are oscillated and maximum 
 6 (i, j). we have: percent overshoot (see Figure 4a). In this case it 
 max 3 3
 xxij # max (3.17) reaching (Cmax- C )/ C =(3-2)/2=50%) with Cmax, 
 t 
 C3 is maximum peak and final value respectively of 
 For any SOCNN, the parameters R, C, I, A(i, 
 the response curve measured from the cellular state. 
j; k, l), B(i, j; k, l), A(i, j; k, l; m, n); B(i, j; k, l; 
 iii). The reserve or the stable strength of SOCNN 
m, n) are boundary constants. So that, the bound 
 higher standard CNN (that is: (X =23)>(X 
on the states of the cells, x is finited and can be SOCNN CNN
 max =3)).
calculated by equation (3.10b).
4. Simulation of the Second-Order CNN
 In this section, we will present an example 
to illustrate how the SOCNN described in section 
2 work. Suppose we have the networks 4*4 (N=4, 
M=4) with r=1, we have neighborhood system (see 
Appendix). Data for standard CNN and SOCNN 
feedback and input matrix are choose equal each 
other and similar to [2], that as:
 SR0 1 0WV
 S W
 A(i, j; k, l)=A(i, j; k, l; m, n)=A= S1 2 0W
 S W
 S0 1 0W
 T X Figure 4a. The transient behaviors of standard 
 input matrix: B(i, j; k, l)=B(i, j; k, l; m, n)=B CNN [2]
Khoa học & Công nghệ - Số 27/Tháng 9 - 2020 Journal of Science and Technology 95
ISSN 2354-0575
 bounded parameter assumptions. ii) We proposed 
 the conditions for the existence and stability 
 of solutions of CNN by choosing appropriate 
 Lyapunov function. iii) We have also used Matlab 
 Simulink software to illustrate and compare some 
 dynamic properties of simple CNN with SOCNN. 
 Some advantages of SOCNN compared to CNN 
 are presented in the section 4.
 There are many theorical and practical 
 Figure 4b. The transient behaviors of SOCNN
 problems to be solved in our future research on this 
5. Conclusion subject, for example, learning problems, associative 
 In the paper, we have tree contributions: i) memory of SOCNN. Nevertheless some rather 
We have presented the architecture SOCNN with impressive and promising application have already 
the 2nd-order polynomial inputs and extended been archieved and was reported in paper [8]. 
References
 [1]. Zuda Huang, Lequn Peng, Min Xu. “Anti-Periodic Solutions for High-Order Cellular Neural 
 Networks with Time-Varying Delays. Electronic Journal of Differential Equations”, 2010, Vol. 2010, 
 No. 59.
 [2]. Leon O. Chua and Lin Yang “Cellular Neural Networks: Theory”, IEEE Trans. on Circuits and 
 Systems, October 1988, Vol. 35 No 10.
 [3]. Angela Slavova “Cellular Neural Networks: Dynamics and Modeling”, Kluwer Academic 
 Publishers, 2003.
 [4]. Hoan Nguyen Quang, “On Stability of Hopfield Neural Networks and Application Ability in Robot 
 Control”. PhD. Dissertation, 1996.
 [5]. Valerio Cimagalli and Marco Balsi. “Cellular Neural Networks: A Review”. Proceedings Italian 
 of 6-th Workshop on Parallel Architecture and Neural Networks. Vietri sul Mare, Italy, May 12-14, 
 1993. Wold Scientific (E.Caianiello, ed.)
 [6]. Pier Paolo-Civalleri and Marco Gilli. “On Stability of Cellular Neural Networks” Journal of VLSI 
 Signal Processing 23, 1999, pp. 429-435.
 [7]. Tamas Roska. “Cellular Wave Computers for Brain-Like Spatial-Temporal Sensory Computing”. 
 IEEE ” Circuits and Systems Magazine 1531-636X/5520.000c, 2005.
 [8]. Nguyen Tai Tuyen, Nguyen Quang Hoan, “An Application of Multi-Interaction Cellular Neural 
 Network on the Basis of STM32 and FPGA”, International Journal for Research in Applied Science 
 & Engineering Technology, January 2018, Volume 6 Issue I.
 [9]. Makoto Itoh, Leon o. Chua. “Star Cellular Neural Networks for Associative and Dynamic 
 Memories. International Journal of Bifurcation and Chaos, 2004, Vol. 14, No. 5, World Scientific 
 Publishing Company, pp. 1725–1772.
 KIẾN TRÚC VÀ ỔN ĐỊNH CỦA MẠNG NƠ RON TẾ BÀO BẬC HAI
Tóm tắt: 
 Trong bài báo này, chúng tôi nghiên cứu và đề xuất: i) kiến trúc mạng nơn tế bào bậc hai dựa trên 
mạng nơ ron tế bào chuẩn của Leon O.Chua với các đầu vào ngoài, đầu vào phản hồi và với các điều kiện 
ràng buộc giả định. ii) Các điều kiện cho tồn tại và ổn định các nghiệm của mạng SOCNN được trình bày 
bằng cách tìm các hàm Lyapunov thích hợp. iii) Các kết quả mô phỏng được tính toán trên phần mềm 
Matlab.
Từ khóa: Mạng nơ ron tế bào bậc hai, hàm Lyapunov, tính ổn định.
96 Khoa học & Công nghệ - Số 27/Tháng 9 - 2020 Journal of Science and Technology
 ISSN 2354-0575
 Appendix. Array 4*4 Second-Order CNN Simulation on Matlab
Khoa học & Công nghệ - Số 27/Tháng 9 - 2020 Journal of Science and Technology 97